广告
动力总成悬置系统疲劳强度试验标准的研究
2021-10-08 10:08:47· 来源：汽车NVH云讲堂
摘 要本文以某轿车动力总成悬置系统疲劳强度试验为例，对发动机侧悬置展开详细介绍了悬置系统疲劳强度试验方案、载荷测量、载荷压缩技术和试验结果分析。通过三
摘 要
本文以某轿车动力总成悬置系统疲劳强度试验为例，对发动机侧悬置展开详细介绍了悬置系统疲劳强度试验方案、载荷测量、载荷压缩技术和试验结果分析。通过三组动态试验考核动力总成悬置系统的疲劳强度，最终建立一套可靠的疲劳强度试验标准。
关键词
动力总成悬置系统，试验方案设计，载荷采集，载荷压缩，试验结果分析
1. 引言
动力总成悬置系统作为动力总成与车架/底盘之间的弹性连接系统.从隔振的角度来说，要求悬置刚度越小越好，以将振动隔离至最小；而从支承和限位的角度而言，考虑到空间结构的局限性，要求悬置刚度越大越好，以避免动力总成在极端载荷冲击下产生很大的位移，影响动力输出，甚至与发动机舱某些部位产生干涉[1]。同时，随着用户对舒适性要求的不断提高，各种具有多段隔振特性的液压悬置系统被逐渐推广。这样在大大提高动力总成悬置系统减震特性的同时，对悬置系统的疲劳耐久性和整个寿命周期内的性能稳定性提出了更高的要求。
本文以某轿车橫置动力总成悬置系统疲劳验证开发为例，根据发动机侧悬置系统展开详细介，1) 悬置系统总体疲劳强度试验台架设计方案；2) 数据采集方案；3) 基于损伤等效的载荷压缩；4) 试验台架设计；5) 试验结果分析；6) 总结形成悬置系统疲劳强度试验标准。
2. 动力总成悬置系统试验台架设计方案
2.1. 悬置系统布置特点和受力分析
动力总成悬置按分布位置分类，一般可分为发动机侧悬置和变速箱侧悬置。通常发动机侧悬置多采用液压悬置，主要为了尽可能的衰减发动机燃烧和旋转运动引起的剧烈震动，故为纵向(X)和垂向(Z) 2个自由度方向上约束[1]；相比较而言，变速箱侧悬置一般采用橡胶悬置，除了衰减震动外并提供动力总成的横向限位，故为纵向(X)、侧向(Y)和垂向(Z) 3 个自由度方向上约束[1]。
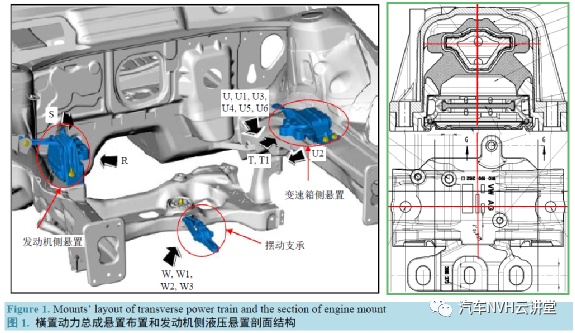
图1 为本文所涉及的橫置动力总成悬置总成布置和发动机侧液压悬置剖面结构。
2.2.1. 悬置系统总成道路模拟试验
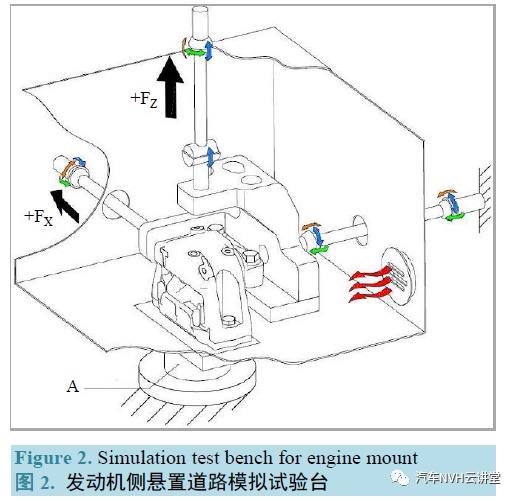
由于悬置系统总成为纯橡胶弹性体或橡胶弹性体和液压阻尼减震模块合成，表现为典型的粘弹性材料特性，呈现出各向异性和多段非线性刚度。所以其受力与频率密切相关。因此，对于发动机侧悬置，采用2 自由度(纵向和垂向)道路模拟试验，图2 为发动机侧悬置2 自由度(纵向和垂向)道路模拟试验台架草图。同时，引入多轴雨流投影技术对道路载荷进行基于损伤等效的压缩，从而实现多轴载荷道路模拟加速试验。具体载荷压缩在下一章节详细展开。
2.2.2. 悬置系统部件——金属支架强化试验
悬置系统与发动机侧连接支架为铝制金属件，在一定频率范围内(通常在100 Hz 以内)，加载频率对金属疲劳强度无影响[2]-[4]。为了保证试件实际主应力平面不变和考虑到主要承受纵向和垂向载荷引起的弯矩，故以支架纵向和垂向道路应变为载荷目标，采用2 轴峰谷值切片定频加试验，即通过峰谷值切片抽取技术[5] (Peak Valley Slicing)提取纵向和垂向的峰谷值并保留其两者间相位关系，并按照试验台可实现的最大频率来重构峰谷值序列实现试验加速，这样确保载荷损伤最大化保留和载荷间相位关系正确[2]-[4]。
2.2.3. 悬置系统部件——金属壳体强化试验
悬置壳体固定于车架上，用于承受由支架传递到纯橡胶弹性体或橡胶弹性体和液压阻尼减震模块合成体上的所有载荷。考虑到纵向和垂向在壳体的作用点各不相同，从简化试验台的角度出发，对于发动机侧悬置的壳体，分拆为2 个单轴多级定频加载试验。即根据传统八级加载法原理[2]-[4]，以支架各向独立应变为主，在每个单独载荷方向上，将道路载荷损伤等效为多级正弦加载序列(Block Cycle) [5]，并按照试验台可实现的最大频率来加速试验频率，从而实现试验简化和加速。
3. 载荷测量方案和试验路面选择
3.1. 载荷测量方案
鉴于前置–前驱动力总成的主减速器仅位于前轴，其作用在动力总成上的驱动反力矩较其他驱动形式大，所以对悬置极限工况下的静刚度要求更高。故采用前置–前驱式动力总成的车辆作为测量目标车辆。
为了有效地获得动力总成悬置系统及部件的实际受力情况和温度环境，主要采取应变片、测量轮、加速度传感器、温度传感器等多种测量手段。其中以应变测量为主，借助CAD/CAE 计算分析结果找出零件各个受力方向的敏感位置并利用惠斯顿电桥加减特性合理布片，如图3，最大层度上把各个方向上的应变完全解耦，从而获得“纯净”的单方向敏感的应变通道，并在黏贴后台通过台架加载验证解耦效果。
3.2. 试验路面选择
鉴于橫置动力总成悬置系统受力特性，除了考虑路面不平整引起的载荷外，还必须考虑人为操控引起的载荷。因此，在载荷测量时，除了选取一些典型的强化道路外，还需要兼顾交变耐久道路和动态试验区的特殊工况，具体表1。
4. 基于多轴雨流投影的多轴载荷压缩技术[6]
为了进一步缩短试验时间，这里把悬置系统总成道路模拟试验的道路载荷谱基于多轴雨流投影进行载荷压缩(过滤)。
4.1. 多轴雨流投影概念
基于线弹性理论可知，物体局部的应力张量
可以表示为：
这里
为载荷贡献因子(权重)，
为载荷方向因子，为外部载荷。
通常，基于
描述的载荷传递路径是很难完全获得的或者说仅能通过广义有限元计算获得。此外，对于优化设计的结构来说，关键应力位置更是无法精确预知的。所以通常无法从外部载荷Lk (t) 直接简单的精确计算局部应力时间历程
。
但对于台架试验来说，既要尽可能压缩载荷，又要能够精确模拟多轴载荷的相互耦合。因此更迫切需要采用压缩的载荷
，即局部应力时间历程
。所以为了实现多轴载荷的压缩，必须要确保压缩后的载荷
保留了原有多轴载荷的雨流属性。从上述载荷路径的描述来看，如果能获得所有传递路径上的载荷方向(投影方向)，那么基于雨流投影方向上多轴载荷压缩是可以被实现的：
这里 β 为单位向量，用于实现原始载荷 L k( t )向压缩载荷
的转化。这就是多轴雨流投影技术的概念假设。通过这样的假设，那么所有成熟的被广泛接受和认可的基于单轴雨流计数法均可以被直接扩展到多轴载荷上，即各个载荷方向(投影方向)上的(单轴)雨流属性。当然，从这里具体案例分析看，可以把这里定义的“各个方向”缩减到“许多主要方向”上投影(通常，鉴于存储和计算速度，一般多轴的数量被限制在6 个自由度以下)。
4.2. 雨流投影方向矢量的构造
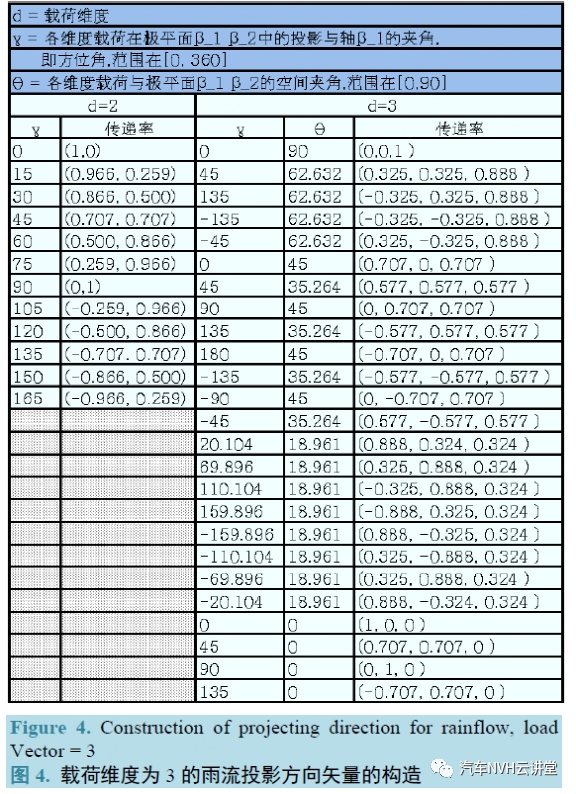
通常对于载荷维度为2 的，其投影方向矢量可用15 度等分半圆极平面来构造；而对于载荷维度为3的，其投影方向矢量可基于半球体，并以极平面加方向角来构造，如图4。
4.3. 投影方向矢量上雨流矩阵的滞后环滤波方程构造(压缩)
所谓多轴雨流计算其实质是在各投影方向矢量平面上基于单轴雨流计数方式来计算各方向矢量平面上结果的集合。同时，为了方便比较各投影方向矢量平面上雨流矩阵，其雨流幅值范围和单位栅格的宽度均是一致的。假设任一投影方向矢量平面上，载荷维度为 d 的时域载荷所得投影幅值范围为
。同样将载荷维度为d 的时域载荷构造为立方体并置于最小包络球体内，如图5。
这是将时域信号
投影到方向矢量平面 β上，可得：
这样该投影方向矢量平面β上，雨流矩阵的信息都可以基于幅值范围UG OG ββ和自定义的N 个幅值格栅来获得。这时，可以根据设定的幅值滤波宽带来对该投影方向矢量平面上的雨流矩阵进行幅值滤波(压缩)。假设滞后环幅值滤波器
，那么滞后环滤波方程可构造为：
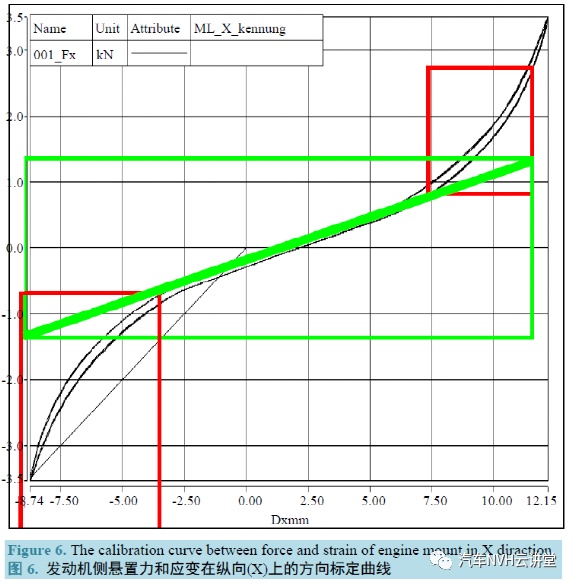
最终，获得该投影方向矢量平面β 上的雨流计算矩阵RFM_β 和余数RES_β。这里，以发动机侧悬置纵向x 方向为例来如何寻找合理的幅值滤波宽带。首先，对悬置支架纵向x 方向进行简单标定，找出力和应变之间的简单标定系数。通过标定所得性能曲线得知，在Fx < −0.8 kN 和Fx > +0.8 kN 范围内，力和位移呈现非线性变化关系，说明橡胶和金属处于紧密触击状态；在−0.8 kN < Fx < +0.8 kN 范围内，力和位移呈现线性关系。因此，可以确定Fx 位于−0.8 kN~+0.8 kN 之间的信号作为主要编辑对象，用于幅值滤波带宽的设定，如下图6。最后，根据力和应变标定系数，将上述力幅值滤波(压缩)范围转换为应变幅值滤波(压缩)范围，再将该应变幅值滤波(压缩)范围除以整个信号应变幅值范围，即获得可用于雨流投影压缩的核心参数–幅值滤波带宽。
总之，为了从整体上获得多轴载荷之间的耦合关系(或相位关系)，多轴雨流投影技术实质就是将多轴载荷投影到精确构造的方向矢量平面上来寻找真正的多轴载荷作用下的主应力平面。其关键就是投影方向矢量平面的构造。
幅值滤波(压缩)范围，再将该应变幅值滤波(压缩)范围除以整个信号应变幅值范围，即获得可用于雨流投影压缩的核心参数–幅值滤波带宽。
总之，为了从整体上获得多轴载荷之间的耦合关系(或相位关系)，多轴雨流投影技术实质就是将多轴载荷投影到精确构造的方向矢量平面上来寻找真正的多轴载荷作用下的主应力平面。其关键就是投影方向矢量平面的构造。
这里必须特别说明的是，前面本文细述了载荷维度为2 和3 的多载荷下方向矢量平面构造，但其均基于半圆或半球。这主要是因为当正半球上基于投影方向矢量平面β 的雨流矩阵已知的情况下，其负半球
上的相应雨流矩阵也就很容易计算出来。此结论可以有以下推理来验证：
因此，可以将投影方向矢量限制在正半球以大大减少计算量，即 d 0 β > 。
4.4. 投影方向矢量平面上相对损伤的计算[2]-[4]
为了方便比较各投影方向矢量平面上的损伤结果，所以只关注相对损伤，不考虑真实损伤或寿命。
这样在所有投影方向矢量平面上的相对损伤计算都基于统一简单的S-N 曲线，无均值应力修正。这也从另一方面证明了S S −β β = ，即负半球 d 0 β < 上的相应雨流矩阵计算可以省略。主要采用基于初级Miner法则的S-N 曲线：
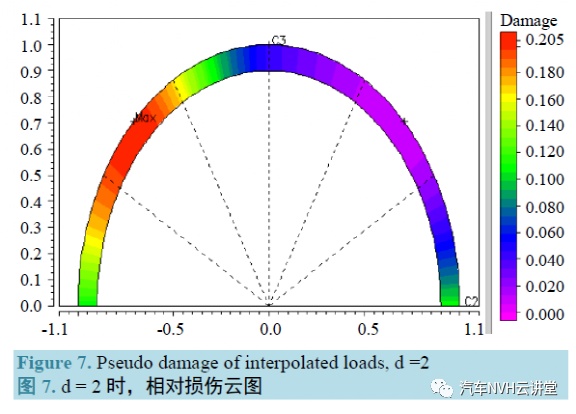
对比各投影方向矢量平面上损伤结果的目的是寻找多轴载荷作用下的空间主应力方向。通常，其潜在的相对损伤可以用贡献因子柱状图和云图来表示，如图7。
另外，这里不得不说明的是由于篇幅的原因，无法针对基于雨流投影的多轴载荷压缩过程中数据存储、多轴载荷压缩后续所需的雨流时域重构法则和多轴载荷时域删除(压缩)进行详述。
5. 试验台架设计
这里以发动机侧悬置系统总成道路模拟试验为例，为了将来广泛快速的开展相应的总成耐久试验，并确保加载到悬置系统总成的载荷为尽可能正确的载荷，即在高频下不受惯性力影响，在台架设计时，在悬置总成底部引入三向载荷测量力传感器，如图8。在完成发动机侧悬置系统总成道路模拟试验应变迭代后，采集悬置总成底部三向力传感器对应的力载荷，并最终将其作为将来其他类似悬置道路模拟的迭代目标信号[7]。
另外，考虑到发动机侧悬置系统总成位于发动机舱内，靠近发动机排气歧管，必须在振动载荷的基础上考虑温度场对弹性体的疲劳寿命和整个寿命周期内的性能稳定性的影响。在道路模拟试验时，引入简易温度箱加热风枪来模拟悬置总成附件的温度环境，更有效的考核悬置总成疲劳强度。
6. 试验结果分析[2]
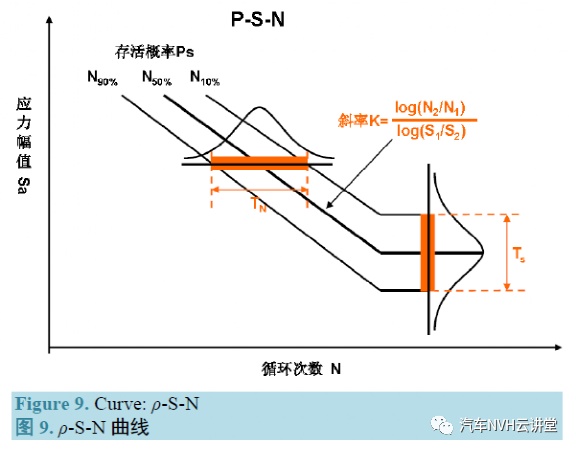
基于ρ -S-N 曲线的实际寿命预测来评估总成或零部件的真实疲劳寿命。ρ -S-N 曲线是一些不同成活率 ρ 下的S-N 曲线族，图 9。
一般情况下，可以近似认为在给定的应力水平下失效循环次数分布(疲劳寿命)或在给定有限寿命下载荷分布，符合正态分布或近似正态分布。通常，ρ -S-N 曲线在有限寿命阶段的HCF 高周疲劳段(103 ~ 106~7 )在双对数坐标系上近似为一直线：
其中 Nρ 是存活率为ρ 时的疲劳寿命；S 是应力；aρ 和bρ 为与存活率有关材料常数。
在已知 3 到4 个总成或零部件实际疲劳寿命或者根据威布尔分布获得试件个数的，可以预测存活率为N50% 的实际总成或零部件的疲劳寿命曲线：其斜率 k 可与目标S-N 曲线相比较，并考虑其与目标S-N曲线的交点，从而评价总成或零部件真实的疲劳寿命。
7. 总结和结束语
通过本文以发动机侧悬置为例，对动力总成悬置系统疲劳试验的研究，可以完整的建立动力总成悬置系统疲劳强度试验认可的试验标准。对于动力总成悬置系统在疲劳强度认可方面具有积极的借鉴意义和工程价值。
致 谢
感谢同济大学汽车学院周鋐教授和MTS 公司金锋高工，在本文写作工程中的大力支持！
作者：李明，周鋐
作者单位：同济大学，汽车学院，上海
来源：Mechanical Engineering and Technology 机械工程与技术, 2015, 4, 141-150
广告
广告
最新资讯
-
NVIDIA 发布 2025 财年第三季度财务报告
2024-11-21 13:30
-
Mack卡车为买家推出创新的虚拟现场探索体验
2024-11-21 13:29
-
氢燃料电池卡车从1到100要多长时间？戴姆勒
2024-11-21 13:28
-
聚焦消费者用车极限环境，2024中国汽研汽车
2024-11-21 13:21
-
新能源汽车高寒环境可靠性行驶试验研究
2024-11-21 13:19
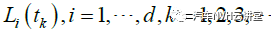
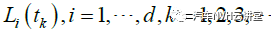
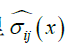
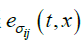
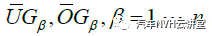
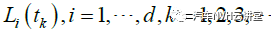
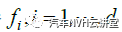
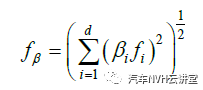
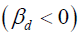
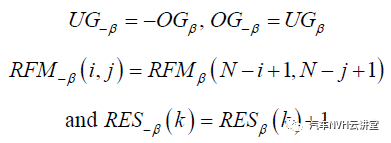
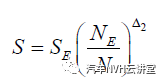
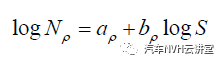
广告
广告
