广告
三种确定动力总成主动悬置LQR控制器加权系数方法的比较
2021-10-10 10:28:54· 来源：汽车NVH之家
作者：陈哲明，王 恒，付江华，陈 宝重庆理工大学 汽车零部件制造及检测技术教育部重点实验室摘要：汽车动力总成主动悬置系统对于提高汽车NVH性及整车品质方面扮
作者：陈哲明，王 恒，付江华，陈 宝
重庆理工大学 汽车零部件制造及检测技术教育部重点实验室
摘要：汽车动力总成主动悬置系统对于提高汽车NVH性及整车品质方面扮演着重要角色，是汽车NVH开发中的重要内容之一。首先建立3自由度1/4车动力总成主动悬置系统模型，应用最优控制理论设计主动悬置系统LQR控制器，其次通过层次分析法、改进的层次分析法及遗传算法对其加权系数进行确定。然后以发动机和路面联合激励下的两种典型工况为系统输入，通过动力总成加速度、悬置动行程、车身加速度及悬架动挠度等评价指标对3种方法确定的LQR控制器主动悬置系统进行评价。结果表明：3种方法确定LQR控制器加权系数的主动悬置，均实现了各性能指标的综合优化，且遗传算法的稳定性和鲁棒性要优于其他两种方法。
摘要：汽车动力总成主动悬置系统对于提高汽车NVH性及整车品质方面扮演着重要角色，是汽车NVH开发中的重要内容之一。首先建立3自由度1/4车动力总成主动悬置系统模型，应用最优控制理论设计主动悬置系统LQR控制器，其次通过层次分析法、改进的层次分析法及遗传算法对其加权系数进行确定。然后以发动机和路面联合激励下的两种典型工况为系统输入，通过动力总成加速度、悬置动行程、车身加速度及悬架动挠度等评价指标对3种方法确定的LQR控制器主动悬置系统进行评价。结果表明：3种方法确定LQR控制器加权系数的主动悬置，均实现了各性能指标的综合优化，且遗传算法的稳定性和鲁棒性要优于其他两种方法。
汽车在路面行驶时，受到来自动力总成发动机的激励和路面不平的激励，会给车内乘员带来极大的不舒适感。而主动悬置系统就是为了解决上述问题而特意安装在动力总成和车身之间的主动隔振系统。
目前对动力总成主动悬置系统的研究主要集中在控制策略上。线性二次型（LQR）控制算法，由于其综合性能优越受到了众多研究者的普遍关注。考虑到LQR 控制器性能指标权重系数直接决定着其控制性能的好坏，因此寻找一种合适且高效的方法来优化LQR控制器中的权重系数显得非常关键。早期研究者们设计主动悬置LQR 控制器一般是采用试错法，即通过计算机反复试算直到控制系统达到期望目标从而确定其加权系数，但该方法费时费力且对系统模型要求较高。文献[7-9]分别采用层次分析法、改进的层次分析法及智能算法对主动悬架LQG控制器加权系数进行了优化，使得控制效果明显提高。但以上研究大都只对主动悬架最优控制器加权系数进行了优化，且只分析比较了某一类方法对最优控制器加权系数的改善情况，很少有对动力总成主动悬置LQR 控制器进行优化同时又对不同方法之间的差异性进行研究的。
本文建立了3 自由度1/4 车主动悬置系统动力学模型，设计了LQR控制器，并采用层次分析法、改进的层次分析法及遗传算法等3种方法对LQR控制器性能指标加权系数进行了确定。通过设置两种典型工况为系统输入，以动力总成加速度、悬置动行程及车身加速度等为评价指标，对不同方法确定的LQR 控制器性能进行分析评价，从而为主动悬置系统LQR控制器加权系数确定提供参考。
1 电磁式主动悬置系统
1.1 电磁式主动悬置结构及原理
本文研究的主动悬置是基于电磁线圈式主动悬置，其结构是在已有被动液压悬置的基础上通过增加电磁作动器部分改造而来，如图1所示。
图1 电磁式主动悬置结构
1 橡胶主簧；2 主液室；3 振动膜；4 流道上盖板；5 可动板；6流道下盖板；7 惯性通道；8 从液室；9 膜片；10 底座；11 线圈；12 内磁芯；13 隔磁套筒；14 气室；15 附加膜；16 真空气管；17 隔磁座；18 外磁芯
其中液体通过惯性通道在主从液室间流动，振动膜通过橡胶与金属骨架连接，主从液室中心的振动膜与电磁作动器的活动线圈相连，这样，当振动膜受到电磁力或液体压力作用时，可沿悬置弹性主轴运动。振动膜运动既受发动机或路面振动导致主簧变形引起主从液室压力波动的影响，又受电磁作动器输出力的调节控制。另一方面，由于振动膜面积小于橡胶主簧等效面积，因此电磁作动器的作用力在一定程度上被放大了，这样设计使得电磁作动器对能耗的需求大大降低，达到了节能的目的。橡胶主簧用来支撑发动机重量，主要负责被动悬置隔振；在主动悬置的里面有由线圈和永久磁铁等组成的电磁作动器，主要用来在汽车不同工况下能根据控制器的调节产生作动力。当电磁作动器遇到故障时，运动线圈可随着振动膜在液体泵吸作用下震荡，此时主动悬置随即变成被动悬置，这样当主动悬置失效时，整个主动悬置系统还有一定的隔振功能。
1.2 3自由度1/4车主动悬置系统模型
建立的3自由度1/4车主动悬置系统模型如图2所示。其中：Me、Mb、Mw 分别为动力总成质量、车身质量和车轮质量，Ke、Kb、Kt 分别为悬置刚度、悬架刚度和轮胎刚度，Ce、Cb为悬置阻尼和悬架阻尼，Fe为发动机激励，F 为主动控制力，q、Xw、Xb、Xe 分别为路面位移、轮胎位移、车身位移和动力总成位移。
图2 3自由度1/4车主动悬置系统模型
根据上述主动悬置系统模型，可得动力总成、车身及轮胎各垂向的振动微分方程如下
2 LQR控制器设计
为了将悬置系统方程转化成用状态空间方程来描述，取状态变量为
则3 自由度1/4 车主动悬置系统的状态空间描述为
式中：A 为7×7 系统状态变量矩阵；B 为7×1 控制力输入矩阵；U为作动器控制力，U=(F)；E为系统激励输入矩阵；W为发动机和路面输入，W=(Fe q)T；C为7阶单位阵；D为7×3阶零矩阵。
取q1,q2,q3,q 4,r 分别为车身质心加速X¨b、发动机质心加速度
、悬架动行程(Xb-Xw)、悬置动行程(Xe-Xb)及电磁作动器主动控制力F 的加权系数。则3自由度主动悬置系统性能函数可写为
取r=6×10-5后将上述加权系数写成矩阵形式如下：q=diag(q1,q2,q3,q4)，代入矩阵Y 和U，则式(6)变换为
代入Y =CX+DU，问题即变为状态控制器调节问题，即
式中：Q=CTqC，为系统状态变量加权矩阵；N=CTqD，为两类变量相关的加权矩阵；R=r+DTqD，为系统控制变量加权矩阵。
当车辆参数和加权系数均确定好后，最优控制反馈增益矩阵K即可由以下Riccati方程求得
由式(9)可求得矩阵P，其中P 为黎卡提方程的解。然后，可求得最优反馈增益矩阵K
在MATLAB中调用LQR控制器设计函数
根据反馈状态变量X即可获得主动悬置系统的最优控制力F
3 确定LQR控制器加权系数
3.1 层次分析法确定加权系数
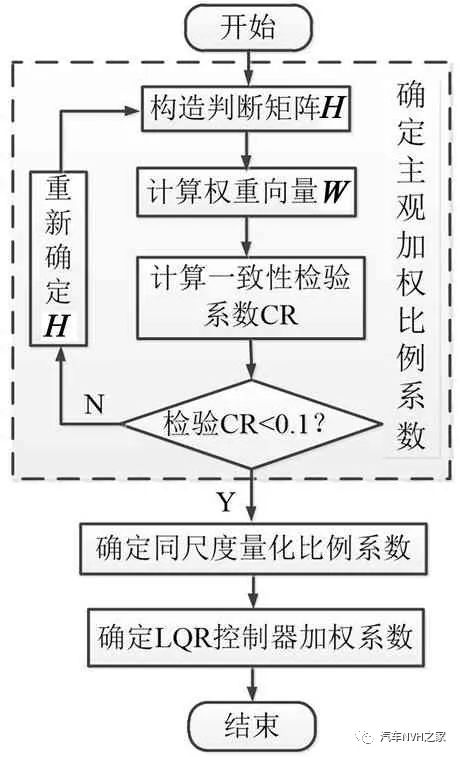
层次分析法（analytic hierarchy process，AHP）是一种针对解决复杂决策问题的权重分析方法。该方法从系统层面考虑系统中各因素对整体的影响，结合了定性分析和定量计算的优势，是一种简洁实用的多准则决策分析方法。基于AHP 确定LQR 控制器加权系数的过程示意图如图3所示。
图3 AHP确定LQR控制器加权系数流程图
其中主要步骤说明如下：
（1）构造判断矩阵H
此过程通过以两个重要度的比率的形式表达两因素之间的重要程度来构建判断矩阵H，以确定每个因素对整体性能指标的重要性的顺序。重要性等级用1～9及其倒数表示，针对本文构造的判断矩阵如下
（2）确定主观加权比例系数
以车身加速度权重系数W1和其对应的主观加权比例系数γ1 =1 为基准，则其他性能指标的主观加权比例系数γi可通过下式换算确定
（3）确定同尺度量化比例系数
为消除不同性能指标单位及数量级不一致带来的影响，需对所有性能指标进行同尺度转化处理。处理办法根据相应被动悬置系统仿真结果所得数据进行，以各性能指标的方差σ 为依据。取车身加速度的同尺度量化比例系数为1，则其他指标的权重系数βi为
（4）确定LQR控制器加权系数
根据最优控制指标的主观加权比例系数γi及同尺度量化比例系数βi，则LQR 控制器的总加权系数qi为
3.2 改进的层次分析法确定加权系数
层次分析是将定性分析与定量分析结合起来，从而确定权重系数，而改进的层次分析法（improved analytic hierarchy process，IAHP）只定性的比较各指标的重要程度，不做定量分析，且无需进行一致性检验，实现起来更加简便。其主要步骤如下：
（1）构造各指标间的两两比较矩阵H′
记hij表示指标i 相对指标j 的重要性大小，该方法重要性等级仅用0、1、2 表示，大大简化了判断过程。针对本文构造的两两比较矩阵如下
（2）计算重要性排序系数ri
（3）构造判断矩阵Bij
式中
（4）计算判断矩阵Bij的传递矩阵Cij
（5）计算传递矩阵Cij的最优传递矩阵Dij
（6）计算判断矩阵Bij的拟优一致矩阵B'ij
（7）计算拟优一致矩阵B'ij的权重排序向量W
该步骤及后续计算按AHP中的步骤进行计算。
总的来说，对比以上2 种方法的原理及实现过程可知：虽然改进层次分析法的计算过程更为繁琐，但由于其决策规则更为简单，且避免了层次分析法中定量分析及进行一致性检验等所引起的前后判断不一致的情况。因此，改进的层次分析法在确定LQR控制器的加权系数时有时更为简单实用。
3.3 遗传算法确定加权系数
遗传算法（genetic algorithm，GA）是根据生物在自然环境中的繁衍进化过程而形成的自适应全局优化搜索算法，具有高效、实用、简便等诸多优点，非常适合用来优化LQR 控制器权重系数。考虑到性能指标X¨b、X¨e、(Xe-Xb)、(Xb-Xw)间的单位和数量均不一致，为了消除由此带来的影响，将其除以相应的被动系统性能指标值，从而得到遗传算法的适应度函数
式中：L为GA的适应度函数；X为优化变量；RMS为系统对应性能指标均方根值。
其中，式(23)用于对优化变量X 进行约束，原理如下：对迭代产生的每一组优化变量X，首先通过式(21)计算适应度函数L，然后由式(23)判断是否满足算法条件。若满足，则上述计算的L即为所得；若不满足，需要对该组优化变量X进行惩罚，惩罚方式是在计算得到的L上加上10，使其远离最小值，从而使得种群向满足约束的方向不断进化。
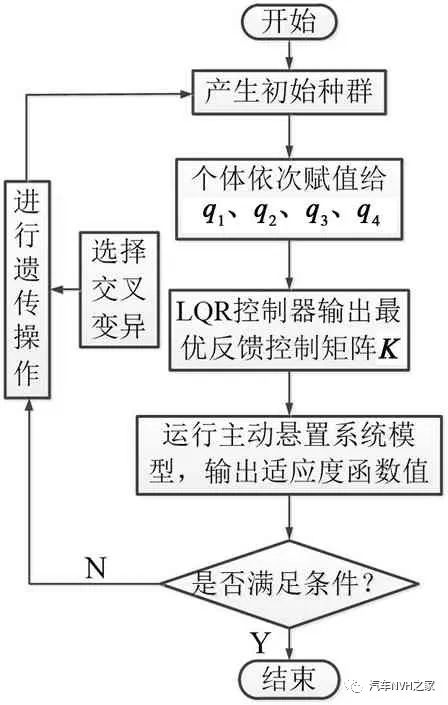
利用GA优化LQR控制器加权系数的流程图如图4所示，基本参数设置如表1所示。其中主要步骤说明如下：
（1）随机产生初始种群；
（2）将初始种群中的个体依次赋值给q1、q2、q3及q4，通过调用式(11)计算最优控制反馈增益矩阵K，由式(12)求得主动悬置系统最优控制力；
（3）通过式(21)计算初始种群中各个体的适应度函数值，并作出判断看是否满足已给定遗传算法的停止条件。满足则直接退出算法，若不满足则重新回到步骤(2)继续寻优；
（4）算法内部进行选择、交叉、变异等操作，重新产生新的个体，并转至步骤(2)，直到算法结束，获得全局最优解。
最后，通过AHP、IAHP 及GA 确定得到的LQR最优反馈增益矩阵K分别如下：
K1≈[5 083.94,355.13,-55 844.52,5 785.72,52 878.07,-6 167.26,-2 133.73]；
K2≈[4 400.86,341.97,-64 482.78,5 593.53,61 513.76,-5 975.29,-1 514.74]；
K3≈[6 773.18,385.17,-37 253.84,6 171.26,34 157.65,-6 566.59,-3 680.29]。
图4 GA优化LQR控制器加权系数流程图
表1 遗传算法的参数设置
4 仿真分析
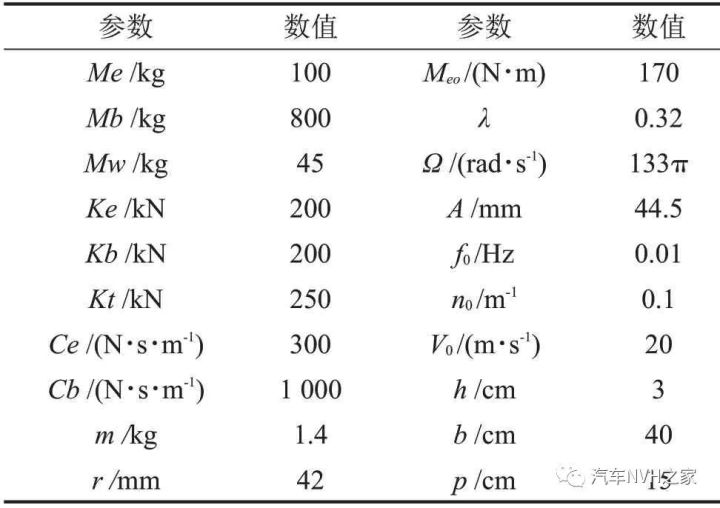
为全面比较本文提出的3种方法，设置2种仿真工况并通过MATLAB/Simulink环境进行仿真验证，仿真主要参数如表2所示。
工况1（常用工况）：以发动机最常用转速工况(n=2 000 r/min)和B 级随机路面联合激励为系统输入。
一般用下式来表示直列四缸发动机的广义激振力[11]
式中：Fy=sinΨ·4mrλω2cos2ωt；
Fz=cosΨ·4mrλω2cos2ωt；Mx=Meo(1+1.3 sin2ωt)；
My=Fz·A；Mz=Fy·A。其中：Ψ 为发动机布置倾角；m为活塞部分质量；r为曲柄回转半径；A为发动机第2、3缸中心线到动力总成质心距离；Meo为发动机输出扭矩；ω 为发动机曲轴角速度；λ 为曲柄半径与连杆长度之比。
常用的滤波白噪声时域路面输入模型用式描述为
式中：f0为下截止频率；Gq(n0)为路面不平度系数；v为车速；w(t)为均匀分布Gauss白噪声。
工况2（冲击工况）:以发动机最常用转速工况(n=2 000 r/min)激励和理想减速带路面的联合激励为系统输入。
理想减速带数学描述如下
式中：h为减速带高度，b为减速带底面宽度，m为减速带垂向水平投影长度。
表2 仿真主要参数
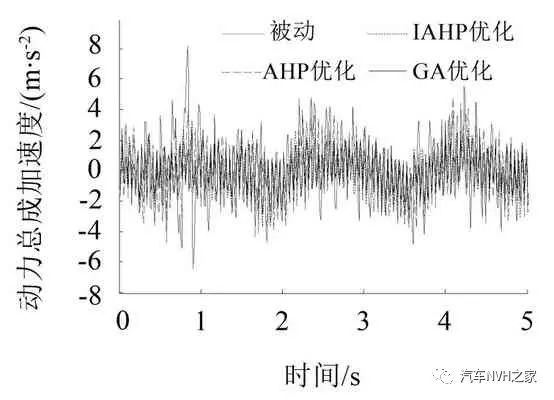
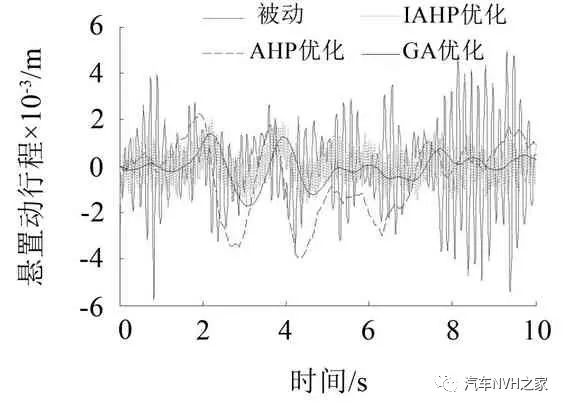
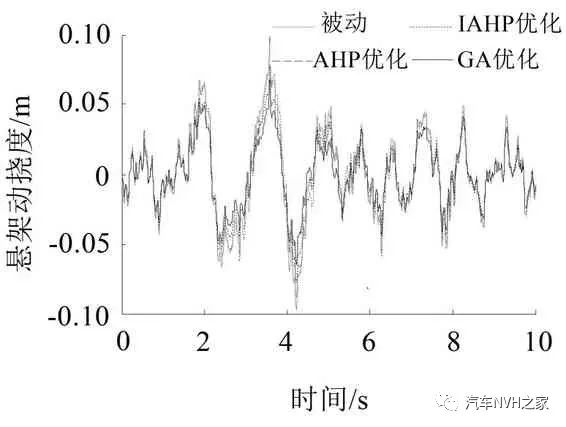
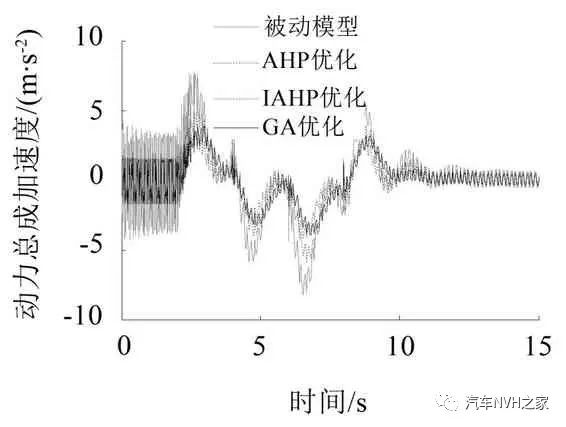
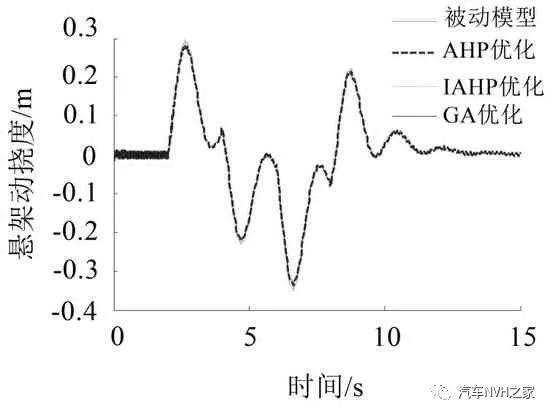
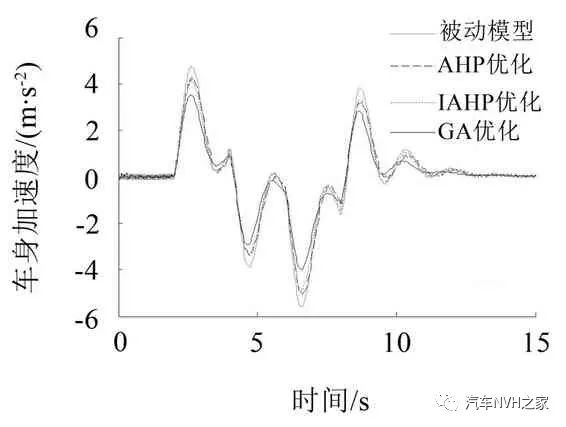
分别以上述2种工况为系统输入，将3种方法得到的最优控制反馈增益矩阵K代入主动悬置模型中进行仿真，得到的动力总成加速度、悬置动行程、车身加速度及悬架动挠度时域响应曲线如图5至图12所示。表3和表4为2 种工况下各性能指标的均方根值。
图5 动力总成加速度
对比分析图5至图8所示的仿真曲线和表3中的数据，经简单计算可知：基于AHP 的主动悬置LQR控制器对动力总成加速度、悬置动行程、车身加速度及悬架动挠度的改善度分别为14.0%、38.5%、0.4%和1.8%；基于IAHP的主动悬置LQR控制器对各性能指标的改善度分别为19.7%、40.1%、5.6%和-0.1%；基于GA 的主动悬置LQR 控制器对各性能指标的改善度分别为21.6%、44.7%、6.1%和0.9%。相比于被动悬置，AHP、IAHP、GA 3 种方法优化LQR控制器权重系数的主动悬置系统均在一定程度上实现了不同性能指标的综合改善，有效提高了动力总成悬置系统的隔振性能。
图6 悬置动行程
图7 车身加速度
图8 悬架动挠度
对比分析图9～图12所示的仿真曲线和表4中的数据可知：基于AHP的主动悬置LQR控制器对动力总成加速度、悬置动行程、车身加速度及悬架动挠度的改善度分别为30.2%、51.1%、5.2%和2.4%；基于IAHP的主动悬置LQR控制器对各性能指标的改善度分别为42.3%、57.8%、8.4%和3.6%；基于GA的主动悬置LQR 控制器对各性能指标的改善度分别为44.7%、60.6%、12.7%和4.9%。
由此可知，采用3 种方法确定LQR 控制器加权系数的主动悬置均能提高车辆在过减速带等恶劣路况的平顺性，同时也说明了3 种方法所设计的主动悬置系统在汽车恶劣工况时具有一定的鲁棒性。
图9 动力总成加速度
表3 工况1输入下各指标均方根值
表4 工况2输入下各指标均方根值
图10 悬置动行程
图11 车身加速度
图12 悬架动挠度
综上所述，虽然AHP、IAHP 和GA 3 种方法均能用于优化主动悬置系统LQR控制器权重系数，但是AHP和IAHP在计算过程中在一定程度上存在着人为确定各性能指标重要性的情况，具有一定的主观性，特别是在对复杂模型进行分析时，会由于控制性能指标增多而导致再采用这两种方法很难确定不同指标的重要性，且此时对于控制器的设计也将变得十分复杂。而GA是一种简单且具有全局搜索能力的智能优化算法，可较好地避免因设计者的主观判断而导致的各性能指标判断不一致的问题，同时可大大缩短控制器的设计时间。因此，GA更适合用于优化主动悬置系统LQR控制器设计。
5 结语
本文在原有被动液压悬置的基础上改造设计了一款电磁式主动悬置，通过对其结构及原理进行分析，建立了3自由度1/4车动力总成主动悬置系统模型。应用最优控制理论设计了主动悬置LQR 控制器，采用层次分析法、改进的层次分析法及遗传算法对LQR控制器加权系数进行了确定。并通过设置2种典型工况，对3 种方法确定的主动悬置系统性能进行了仿真验证，所得结论如下：
(1)3 种方法均能用于优化主动悬置LQR 控制器加权系数，其中层次分析法和改进的层次分析法均存在一定的主观性，且计算相对复杂，不适合用于复杂系统模型中。
(2)相比于被动悬置，3种方法确定的LQR控制器均在一定程度上提高了动力总成悬置系统的隔振性能和整车平顺性，较其他两种方法而言，采用遗传算法确定LQR 控制器加权系数的主动悬置综合性能更好。
广告 
广告
编辑推荐
最新资讯
-
Discount Tire带来直观易懂的轮胎评测体系
2025-01-15 15:15
-
标准动态||中国汽车工程学会标准项目清单
2025-01-15 15:13
-
NI与蔚华科技携手，共建亚太区首座功率半导
2025-01-15 15:10
-
海克斯康（Hexagon）推出虚拟试驾X测试自动
2025-01-15 15:08
-
汽车NVH仿真：打造静谧驾驶体验的关键
2025-01-15 08:27
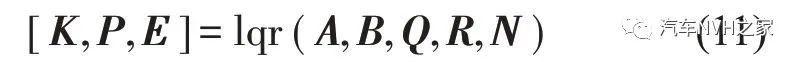
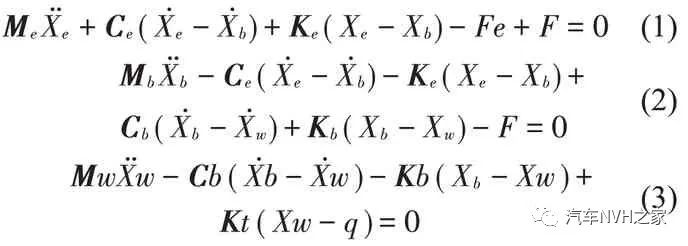
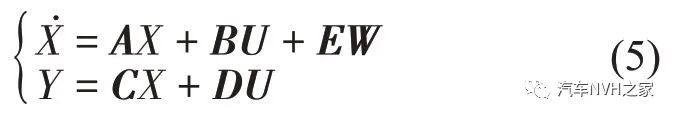
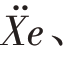
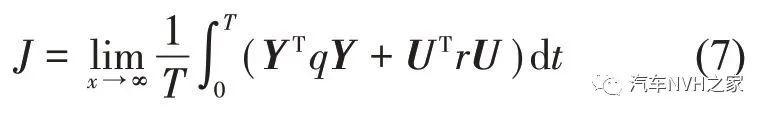
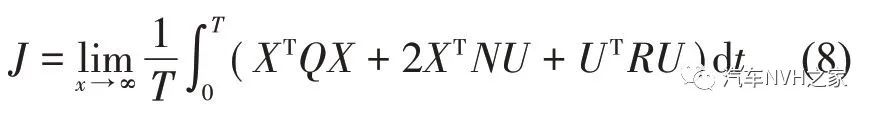
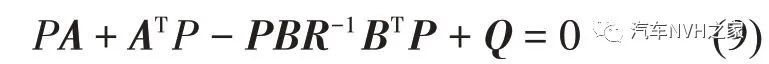
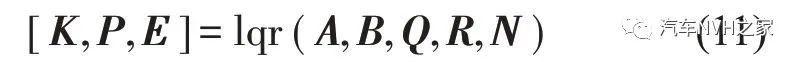
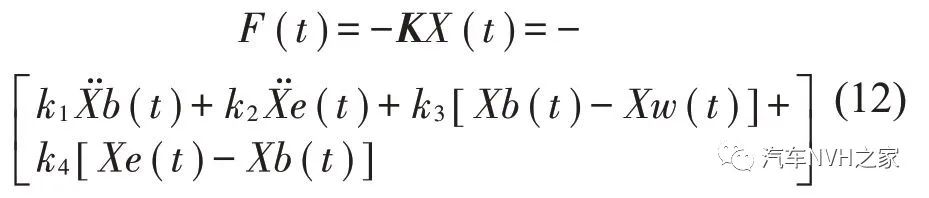
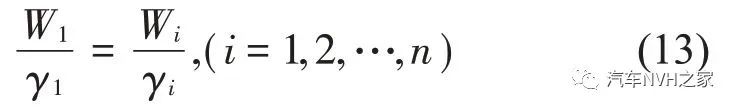
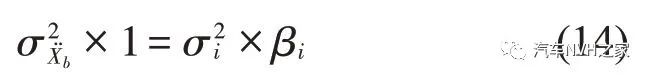
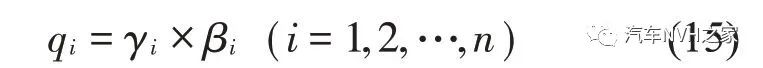
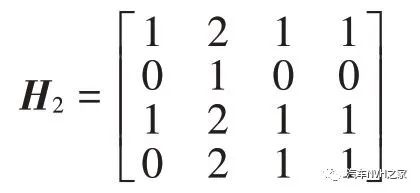
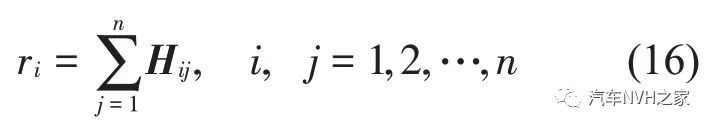
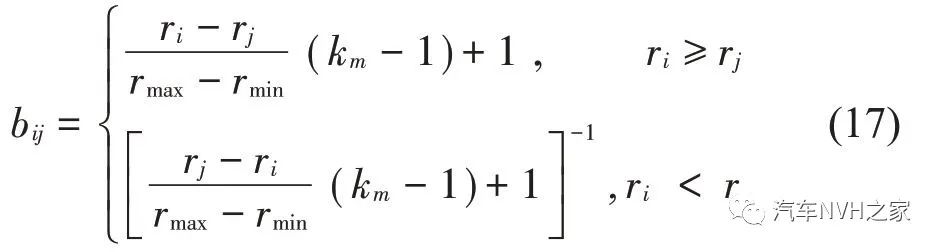
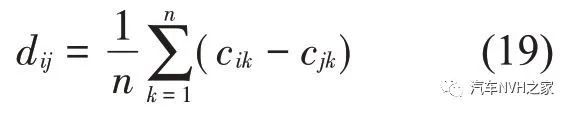
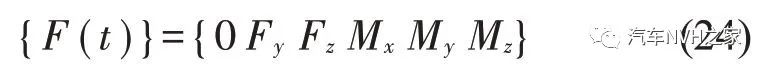
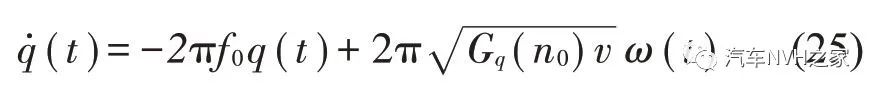
广告
广告
