广告
大型软包锂离子电池的热物性实验研究
2021-10-11 13:43:42· 来源：电动学堂 作者：王帅林等
文章来源：上海理工大学能源与动力工程学院等当前，为了缓解续驶里程及快速充电的焦虑问题，电动汽车电池组的能量密度正逐步提升，这促使锂离子电池单体的尺寸逐
文章来源：上海理工大学能源与动力工程学院等
当前，为了缓解续驶里程及快速充电的焦虑问题，电动汽车电池组的能量密度正逐步提升，这促使锂离子电池单体的尺寸逐渐趋于大型化。电池尺寸的增大会加剧电池温度分布不均匀，加速电池系统的寿命衰减。Gomez等的研究表明，较高的工作温度和温差（≥5°C）可以严重影响锂离子电池的工作性能和循环寿命。对锂离子电池组采取有效的热管理措施十分重要，须分析电池的热物性参数，如比定压热容和导热系数。准确掌握电池的热物性参数，对建立电池的热仿真模型、制定电动汽车电池组的热管理及充放电控制策略等都有积极的指导意义。
以往关于锂离子电池热物性的研究主要集中于小尺寸电池，对于大尺寸软包锂离子电池热物性的研究很少涉及。此外，已有一些研究在测定电池的热参数时不考虑热损的影响，使得测算误差较大。专业测量仪器因测试腔较小，难以满足大尺寸软包锂离子电池的热物性测试需求。
本文基于传热学准稳态导热原理，考虑热损，建立电池的热物性理论模型，研究比定压热容和导热系数与温度的依变关系。以与电池形状相近的块状有机玻璃（亚克力）为标样，对提出的测试方法的有效性进行验证。与以往技术相比，本文研究不依赖专用设备，具有测试周期短、准确度高、测试灵活和测试费用低等优势，为研究人员对大尺寸软包锂离子电池的热物性表征提供了良好的技术支持。
1电池内部传热理论分析
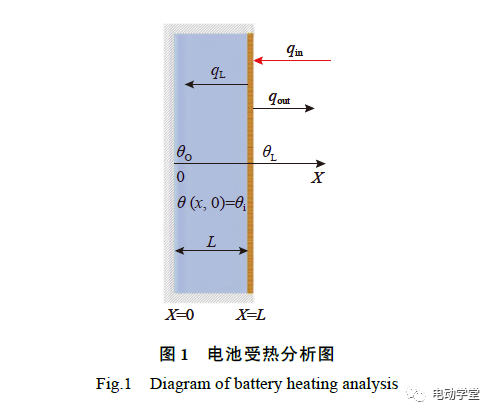
根据传热学的一维导热原理可知，当在紧并的2块软包电池的两对称主面（其他2个主面完整接触）均匀加热时，热流密度线起始于受热面，终止于内侧面（冷面）。因软包电池较薄，沿其4个小侧面的热量损失可以忽略，该传热学问题可以视为沿无限大平板厚度方向的一维导热问题。考虑热量沿电池主面的损失，受热分析如图1所示。图中，L为电池厚度，qin为在电池受热面加载的均匀热流密度，qout为电池受热面因热损而造成的热流损失密度（out going heatflux），qL为从电池受热面流向电池内部的热流密度（在数值上等于qin−qout）。
沿无限大平板厚度方向（x方向）一维导热、非稳态、无内热源，对该问题进行数学描述。建立导热微分方程：
式中：κx、cp分别为电池的法向导热系数和比定压热容，ρ为电池的密度。
边界条件为
式中：θi为电池初始温度。
采用Laplace变换法求解导热微分方程式（1），得到电池温度场在时间和空间上的解析解：
从该解可知，电池的温度场分布包含3个分量（等式右边）：第1个是随时间线性变化的分量，斜率与乘积ρcp成反比，与热流密度成正比；第2个是仅与电池厚度相关的分量；第3个是级数项，由于指数衰减的原因，级数项会随着加热时间的延长而逐渐变小.定量分析表明，当aτ/（L）>0.5时，该级数项数值趋近于0，可以忽略不计。综上所述，可以根据式（5）电池温度场变化曲线的斜率确定电池比定压热容：
由式（6）、（10）可知，只要获得电池受热过程中qin和qout以及电池的温变率dθ/dτ和冷热面间的温差θL−θO等，即可确定电池的比定压热容和法向导热系数。
2 电池热物性实验研究
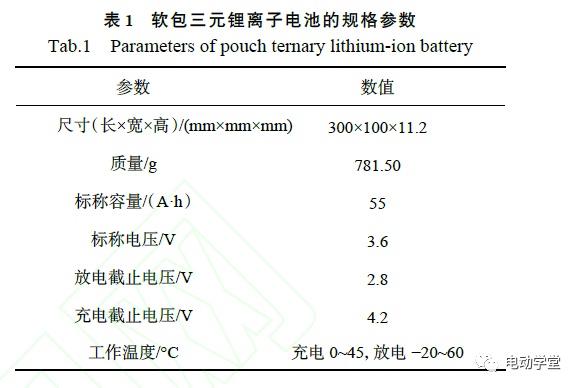
实验对象为车用高比能三元软包锂离子电池，正极为镍钴锰酸锂（Li（Ni0.5Co0.2Mn0.3）O2），负极材料为石墨。电池的规格参数如表1所示。
2.1实验装置
实验中主要用到稳压电源（给加热膜供电）、加热膜、热流计（heat-fluxmeter，HFM）、恒温箱和计算机等设备，其中热流计连接热流传感器（heat flux sensor，HFS），用于监测电池受热面因热损而造成的热流损失qout.实验装置、热电偶（thermo couples，TC）及HFS布置如图2所示。
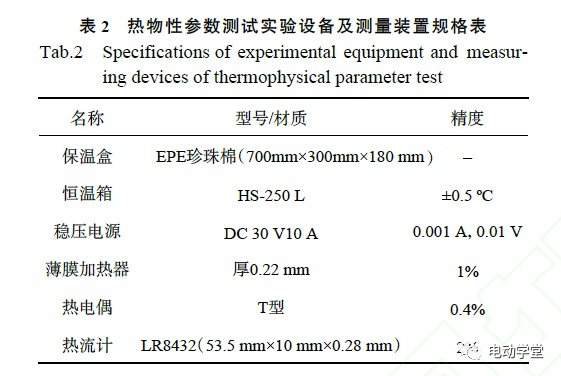
在实验过程中，将2张同规格的加热膜敷于电池（SOC为50%）受热面，如图2（a）所示，并由一台稳压电源给其供电.将2个同规格的热流测头HFS分别布于电池受热面中心，如图2（b）所示，用于监测因热损引起的热流损失。在电池受热面中部距热流测头中心7mm处（在垂直其侧边方向相距2mm处）分别布置1枚T型热电偶TC1和TC2，在电池接触主面中心布置1枚热电偶TC3.将电池置于由珍珠棉（expandable poly-ethylene，EPE）材料制成的保温盒中心，将该保温装置置于恒温箱，由恒温箱提供初始温度和恒定的环境温度。热物性参数测试实验设备和测量装置参数如表2所示。
2.2实验原理及步骤
2.2.1电池受热过程中
表面的温变和热流密度每次测试前，均将恒温箱炉温调至−10°C，静止2h，确保电池温度与环境温度一致。为了减小测试误差，预设电池受热过程中冷、热面间的温差不低于5°C。通过几次实验发现，当输入功率接近140W时，可以使电池冷热面间的温差（温度场达到准稳态后）最大达到11.5°C。为了排除实验的偶然性误差，重复测试3次。
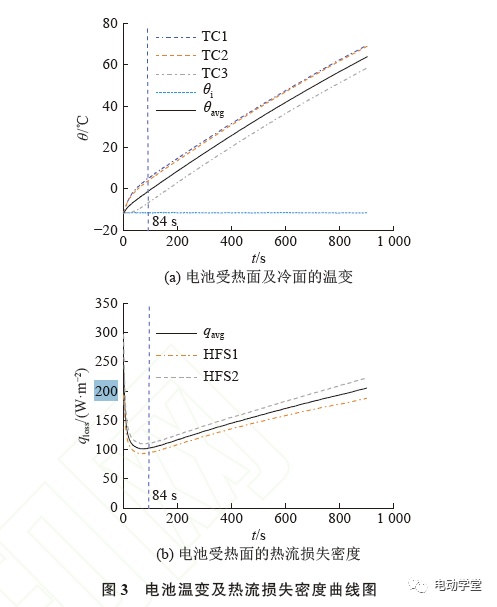
以其中1次测试为例，如图3所示为电池受热过程中表面的温变状况和热流损失变化状况。图中，θavg为电池平均温度，qavg为受热面由热损引起的平均热流损失密度。在测试过程中，为了避免电池温度过高，当最大温度升至70°C时关闭电源。
如图3（a）所示，加热84s后，电池冷热面温变曲线的斜率逐渐趋于稳定，受热面温度在第900s时接近70°C。如图3（b）所示，电池受热面的热流损失。
密度在84s后近乎以线性上升，这主要是因电池与环境间的温差逐渐增大（同时热损增大）所致的。
2.2.2电池的热物性参数计算
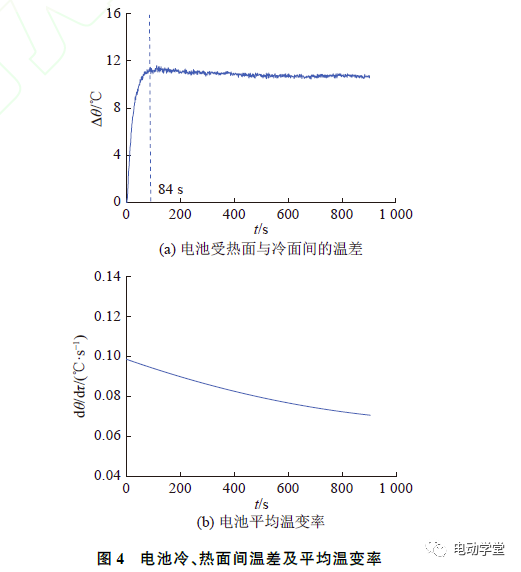
根据图3所示的测试结果，计算电池受热面和冷面间的温差△θ（θL−θO）和电池的平均温变率（dθ/dτ），计算结果分别如图4（a）、（b）所示。
从图4（a）可知，在前84s，电池冷、热面间的温差上升较快；在84s后，该温差趋于稳定，但略向下倾斜，这主要是由热损引起的。由此可知，在加热至84s时电池的温度场达到准稳态。从图4（b）可知，电池的温变率随时间而逐渐下降，该现象是由热损引起的。将图4（a）、（b）所示的数据分别代入式（6）、（10），考虑图3（b）所示的qout，可得电池的比定压热容和法向导热系数。
3结果与讨论
3.1电池测试结果
3.1.1电池比定压热容
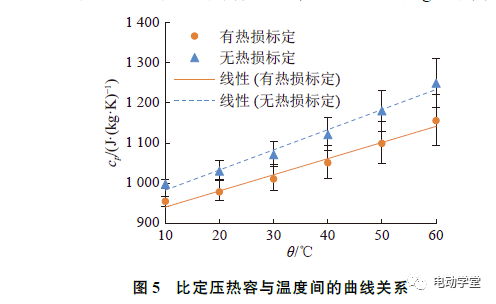
如图5所示为电池比定压热容随温度的变化趋势。可知，电池比定压热容随着温度的升高而增大，当温度从10°C升至60°C时，比定压热容从945。9J/（kg·K）上升到1166.6J/（kg·K），增幅约为21%。有热损标定和无热损标定线性拟合的R²分别为0.9826和0.9784。与不考虑热损的测算结果相比，考虑热损后测得的电池比定压热容降低约6%，且温度越高，两者的偏差越大，这表明热损标定对测算结果具有较大的影响。
电池固体部分的材料是导致上述现象的主要原因。通常，电池的固体部分包括外壳、电极和隔板等，材料的晶格振动能、分子旋转能、电子动能和内能随着电池温度的升高而增大，这4种能量的增加导致电池材料结构熵的增加，因此电池的比定压热容会随着温度的升高而增加。部分研究得到了类似的趋势：Sheng等测得方形磷酸亚铁锂电池温度从−20°C上升至60°C时，比定压热容从1081J/（kg·K）上升至1267J/（kg·K），增大约12%，表明采用不同正极材料的锂离子电池比定压热容具有差异性。Drake等对圆柱形26650和18650磷酸亚铁锂电池比定压热容的测量结果分别为1605和1720J/（kg·K），与本文的测试结果相差较大。一方面是由于笔者在测试过程中，将圆柱形电池视为均质实体，实际上该型电池内部内芯与电池外壳具有一定的空度（普遍距离3~5mm），这使得测试结果偏大；另一方面，笔者未考虑实验过程中热量的损失情况，造成了测量的比定压热容偏大。
3.1.2电池导热系数
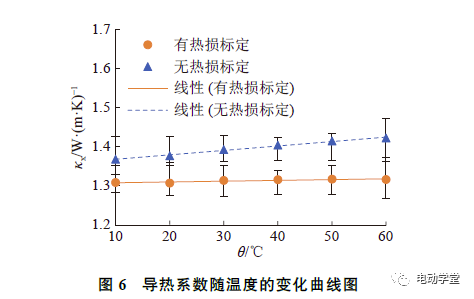
如图6所示为κx随温度的变化趋势。可知，有热损标定的电池导热系数随温度的升高变化较小，平均值为1.313W/（m·K），上下浮动不超过0.5%，受温度的影响可以忽略不计。当温度从10°C升至60°C时，无热损标定的导热系数，增大约4%。有热损标定和无热损标定线性拟合的R²分别为0.9905和0.7943.相比不考虑热损的测算结果，考虑热损后测得的电池导热系数降低约6%，且温度越高，两者偏差越大，这表明热损标定对导热系数的测算结果具有较大的影响。该结果与电池导热系数随温度的变化趋势一致。辛乃龙通过查表及技术手册获取铝箔、铜箔、正负极材料及隔膜的热物性参数，根据串并联热阻原理，计算得到软包电池的导热系数为0.913W/（m·K）。由于忽略了固体之间的热阻，导致测算结果与本文差异较大。
3.2标样测试结果分析
以与电池形状相近的块状有机玻璃（亚克力）为标样，考察本文方法的有效性。有机玻璃的实物图如图7所示，2块玻璃的规格相同，尺寸均为100mm×100mm×10mm。为了匹配有机玻璃的热参数测试，所选加热膜（2张）的尺寸均为100mm×100mm×0.2mm。
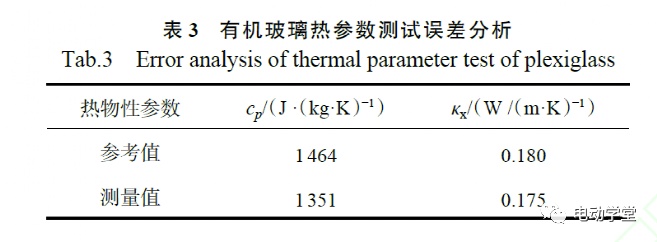
亚克力玻璃的实际热参数与基于本文方法的测算结果如表3所示。
从表3可知，有机玻璃比定压热容和导热系数的测试结果分别为1351J/（kg·K）和0.175W/(m·K），与实际值相比，测试误差分别为7.7%和2.8%，精度不低于92.3%。无热损标定时的误差分别为10%和15%。该分析表明，采用该方法测算电池的热参数具有较高的有效性，采用该方法测试电池的热参数时，热损标定十分关键。
与Drake等的测试方法相比，该方法考虑了热损，测算精度高。与盛雷等采用稳态法测试电池热参数相比，本文方法的测试周期短。本文提出的锂离子电池热物性测试方法可以满足大尺寸软包锂离子电池的热物性测试要求，且该方法属于“原位测试”，不需要拆解电池即可完成测试，测试灵活且安全。采用热损标定的准稳态法测量大尺寸软包锂离子电池的热物性，具有较高的实用性。
3.3实验不确定度分析
根据Moffat提出的不确定性分析方法可知，实验测试结果的不确定度由自变量的平方根确定。导热系数及比定压热容的不确定度可以通过下式估算：
计算结果显示，κx和cp的测算不确定度约为2.3%和2.2%。
4结论
（1）锂离子电池的比定压热容随着温度的升高而线性增大，在10~60°C下，比定压热容增大21%；导热系数受温度的影响较小，受影响的程度远低于比定压热容。
（2）在电池热物性参数的测试过程中，热损标定十分关键。本文实验的验证结果显示，经热损标定后可以提升5%的精度。验证结果显示，该方法的测算精度不低于92.3%，证明了该方法的有效性。
（3）本文方法属于非稳态法，测试过程属于“原位测试”，测试时长不高于900s。本文研究可以为相关动力电池企业提供有效的技术支持，具有较高的工程应用价值。
广告
广告
编辑推荐
最新资讯
-
厂商要多努力，才能让用户听起来毫不费力？
2024-11-22 17:10
-
TOP30！海克斯康入选2024福布斯中国数字科
2024-11-22 15:25
-
揭秘国产装备制造厂商的成功秘籍：好耐电子
2024-11-22 15:24
-
一文详解安全分析方法STPA：以自动紧急制动
2024-11-22 15:20
-
选对涉氢压力表：守护涉氢场所安全的关键一
2024-11-22 15:19
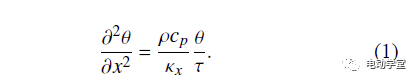
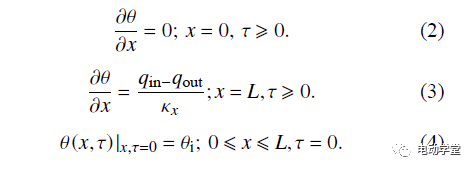
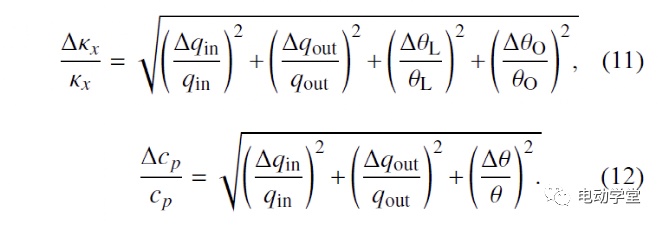
广告
广告
