广告
王博聊声学 | 闲聊HBK噪声源识别系统的发展史
2021-10-13 12:50:30· 来源：BK声学与振动
王 博 说对于工业界的振动噪声问题，往往最困扰工程师的问题是噪声是从哪儿来的？这一难题不仅激励着科研人员在技术方法上不断地深入探索，也催生了各种各样的商
王 博 说
对于工业界的振动噪声问题，往往最困扰工程师的问题是——噪声是从哪儿来的？
这一难题不仅激励着科研人员在技术方法上不断地深入探索，也催生了各种各样的商业化系统试图解决这一实际工程问题。
今天，我们简要回顾HBK在这一领域的发展历程，向各位看官展示我们引以为傲的技术与产品，并与大家探讨未来的发展方向。
王博聊声学
01、上世纪80年代
上世纪80年代，美国宾夕法尼亚州立大学的E. G. Williams、J. D. Maynard和E. Skudrzyk等建立了近场声全息理论（Nearfield Acoustic Holography, NAH），这是一种有效识别低频噪声源的方法。它基于空间Fourier变换原理（Spatial Transformation of SoundField, STSF），通过采集规则面上均匀网格点的声场信息，变换到波数域进行声场递推，再反变换得到声源面的声压、声强或质点振速分布。
我们在80年代后期，推出了基于STSF的噪声源识别系统，这是世界上第一套商业化声全息系统。这套系统的秘籍在于多参考的互谱测量，即在声源附近设置多个参考传感器，其数目大于等于潜在的声源数目，通过扫描测量获得测量点与参考点之间的互谱，提取代表声场信息的主成分，再进行NAH空间变换，如图1。这非常适用于实际中存在的多个不相干的声源情况，但同时局限于稳态工况。
图1
那么对非稳态的声源如何进行声全息成像呢？例如汽车发动机的升降速，越来越严格的法规驱使汽车制造商努力减少外部辐射噪声。在1993-1996年，欧洲Brite-Euram研究性项目PIANO提出利用新方法对重型汽车的通过噪声进行更快、更廉价且更准确地测试。在此背景下，我们开发了一套基于全新时域声全息（Time Domain Holography, TDH）的系统，成功应用于此项目的声场评估。该系统能够告诉我们噪声是从哪里辐射的，什么时候辐射的，但它要求所有测点必须同时测量，如图2，这意味着需要大通道系统，这在当时对硬件性能和成本都提出了巨大挑战。
图2
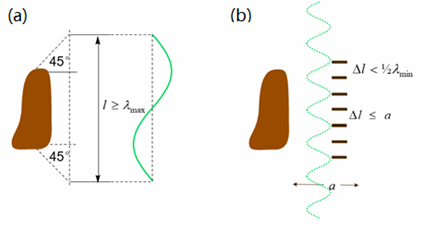
可见，早期的系统对硬件的要求很高，测试也非常麻烦。STSF方法虽然能够有效识别声源位置，但要求阵列面是规则的平面、圆柱面或球面，传声器必须是均匀等间隔分布。声源的面积越大，阵列的尺寸则要求越大，通常阵列面不仅要覆盖整个声源面，还要外延45°张角，如图3(a)。如果声源的频率越高，传声器的间距则要求越小，通常要小于最高频率的半个波长，如图3(b)，如果,那么最高频率约为1500Hz。可以想象，做一次试验需要至少上百个测量点。这在当时，也只有土豪才能买得起这样的系统。
图3
02、进入2000年
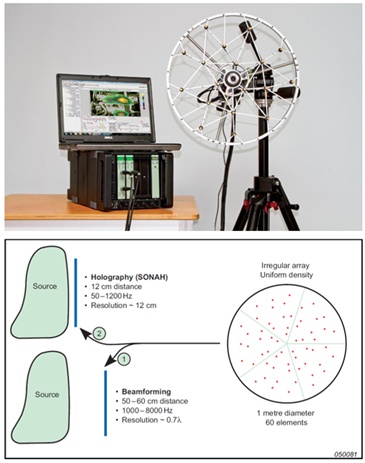
一眨眼千禧年到来了，我们的噪声源识别系统也进入了快速发展时期。为了拓展上限频率，我们引入波束形成（Beamforming）方法。这是一种针对中高频声源、中远距离测量的方法，通过估计阵列前方来自不同入射方向平面波（或球面波）的幅值，来估计声源的方位。与STSF方法相比，波束形成不要求声阵列的尺寸大于声源面，另外传声器的分布是随机的，这样使用较少的传声器也能在很高的频率下获得可接受的空间混叠效应，直白地说，就是使用较少的传声器就能获得很高频率的声源分布。
波束形成的成像效果很大程度上由声阵列的设计决定。为了更大程度地降低最大旁瓣级（即声源云图上出现的虚假鬼影），我们优化了阵列设计算法，使得在给定的频率范围内能够有效降低最大旁瓣级。2002年我们推出的轮形阵列就是依据此算法设计的。图4是用于高铁移动声源波束形成的轮形阵列，直径为4m，共78个通道。每一条轮辐上安装6个传声器，用一根线缆连接到采集模块阵列面板的一个LEMO接头上，这一个LEMO接头就代表6个输入通道，这样极大简化了线缆布置，有利于通道检测和传感器校准。
图4
03、2005年的必杀技
到这里不知各位看官发现没有，STSF和波束形成就是一对矛盾体，一个针对低频声源，一个针对中高频声源；一个要求传声器均匀布置，一个要求随机布置；一个要求近场测量，一个要求远场测量；一个要求声阵列大于声源面，一个则可以小于声源面。对于实际工程问题怎么破？难道要背着两套阵列去查找声源？能否让这两个矛盾体化干戈为玉帛？
为了同时满足全频段的声源识别，B&K于2005年使出了必杀技——统计最优近场声全息（Statistically Optimal NAH, SONAH）。这是一种完全在空间域进行计算的方法，将空间声场看作是平面波的叠加，利用传声器阵列数据的线性组合估计声源分布。SONAH避免了STSF空间Fourier变换带来的误差（卷绕误差和窗效应）和对阵列的严格要求，不仅可以利用传声器随机分布的阵列，也可以使用小尺寸的阵列，即低频时阵列的尺寸可以显著小于一个波长，成像精度和空间分辨率也明显提高。
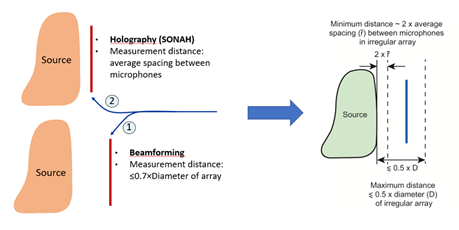
SONAH方法完美规避了STSF方法的限制，用同一个阵列，低频时采用SONAH方法而对于中高频声源采用波束形成方法，这样的组合我们称为Combo阵列，如图5。这样，我们使用一套阵列系统，就可以实现全频段的噪声源识别。这在当时属于重大突破和创新，其理论思想至今都发挥着重要的影响。
图5
04、2005年以后
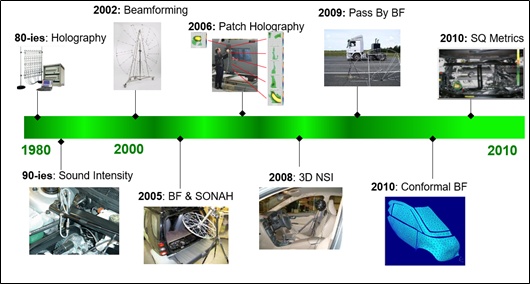
Combo阵列推出后，市场反映热烈，成为我们卖的最火的阵列产品。与此同时，我们也继续发力，2006年手持式阵列进行局部声全息成像，2008年球形阵列用于封闭空间的360°成像，2009年汽车通过噪声波束形成，2010年保形成像和声品质参数成像，2011年精细化波束形成和新的阵列设计，2012年高铁移动声源波束形成和手持式阵列高级算法，2015年飞机飞越噪声源识别，2019年风洞测量的麦克风互谱矩阵降噪方法等。
图6
图7
05、2015年再次祭出必杀技
最近10年是噪声源识别技术最火的时期，标志性的事件是压缩感知（Compressive Sensing, CS）技术在这个领域的成功应用。如果声源在空间分布是稀疏的，或者空间声场在某个基函数上的表达是稀疏的，那么我们就有可能通过较少的随机测量点求解其空间分布。什么意思？就是今后我们可以用较少的传声器获得比以前更高精度和更高频率范围的结果啦。还是没明白？请查阅我们总部专家Jorgen Hald的文章Fastwideband acoustical holography，发表于J.Acoust. Soc. Am. 139 (4), April 2016。
我们于2015年提出了宽带声全息技术（Wideband Holography, WBH），就是基于压缩感知理论。WBH将声源模型建模为一系列离散的单极子点声源，间距小于半个波长，并认为真实声源分布是稀疏的。不同于用L1范数最小化来约束稀疏性，WBH提出了用迭代方法不断地移除与真实声源相关的鬼影。其计算效率更高，计算时间缩短了约30倍。并且，支持大动态范围的声源重建，即存在强声源时也能够准确识别弱声源，而不会出现计算数值不稳定情况。
在此之前，我们使用图5的Combo阵列进行声源识别时，需要近场测量一次，测量距离约为传声器的间距，进行低频SONAH计算；再远场测量一次，测量距离≤阵列直径的0.7倍，进行波束形成计算。有了这项技术，我们仅测量一次，测量距离一般大于传声器间距的2倍，小于阵列直径的一半，就可实现全频段的噪声源识别，如图8。这对于非稳态工况、不易复现的工况或者做一次实验太烧钱的情况，具有重要的意义。
图8
除了一次测量和一次计算就完成整个频率范围的声成像外，WBH还有很多优势，例如：
-
与延迟求和波束形成相比，能够显著降低旁瓣鬼影的影响
-
与精细化波束形成相比，能够很好地应用于相干声源
-
在整个频段都有很好的空间分辨率，低频时类似于SONAH，高频时类似精细化波束形成
-
存在强噪声源的情况下也可以很好地识别弱噪声源
-
在整个频段都有很好的声功率估计
近年来，方便携带、快速成像、实时显示成为客户的首要要求。为此，我们同年推出了声学摄像机Acoustic Camera（图9），它基于最新的BK Connect软件平台，满足客户所有的期待，成功吸引众多用户的兴趣。
图9
展望未来，随着智能传感、5G传输、大数据、人工智能等成功落地，今后的噪声源识别系统会是怎样的？欢迎小伙伴们积极留言，与我们共同探讨未来发展之路。
参 考 文 献
1. B&K Technical Review 1 – 1989, STSF — A Unique Technique for scan based Near-FieldAcoustic Holography without restrictions on coherence
2. B&K Technical Review 1 – 2000, Non-stationary STSF
3. B&K Technical Review 1 – 2005, Combined NAH and Beamforming Using the Same Array
4. B&K Technical Review 1 – 2015, Fast Wideband Acoustical Holography
您还可以通过如下方式联系我们，了解更多产品与应用详情：
邮箱：cn.info@bksv.com
网址：www.bksv.cn
电话：400-900-3165（周一至周五9:00-18:00）
广告 
广告
最新资讯
-
系统级封装（SiP）在新能源汽车领域的应用
2024-12-23 08:51
-
车载通信框架 --- 智能汽车车载通信架构浅
2024-12-23 08:40
-
全国首例！武汉车网智联公司完成智能网联测
2024-12-23 08:39
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
广告
广告
