广告
基于优化嵌入强化学习的环岛场景下自动驾驶自适应决策方法研究
2021-10-27 00:26:18· 来源：同济智能汽车研究所
编者按：环岛是一种复杂的驾驶场景，在该场景下车辆需要进行进入、驶出、换道等操作，此外，环形道路更增加了驾驶复杂性。近年来，强化学习以其独特的与环境的交
编者按：环岛是一种复杂的驾驶场景，在该场景下车辆需要进行进入、驶出、换道等操作，此外，环形道路更增加了驾驶复杂性。近年来，强化学习以其独特的与环境的交互能力和自学习能力在自动驾驶决策问题上得到广泛应用。本文将强化学习方法应用于环岛驾驶场景，利用强化学习得到决策变量，然后输入给下层非线性MPC控制器进行跟踪。仿真结果证明该方法具有较高计算效率和更好的性能。
本文译自：《Adaptive Decision-Makingfor Automated Vehicles Under Roundabout Scenarios Using Optimization EmbeddedReinforcement Learning》
文章来源：IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS
作者：Yuxiang Zhang , Bingzhao Gao , Lulu Guo , Hongyan Guo and Hong Chen
原文链接：https://ieeexplore.ieee.org/document/9311168
摘要：环岛是一个典型的可变、交互式场景，在该场景中，自动驾驶车辆应做出自适应和安全的决策。本文提出了一种优化嵌入式强化学习（OERL）方法来实现环形交叉口下的自适应决策。本文的改进是对Actor-Critic框架中actor的修正，将基于模型的优化方法嵌入到强化学习中，以直接探索动作空间中的连续行为。因此，所提出的方法能够以较高的采样效率同时宏观行为（是否改变车道）和中尺度行为（期望加速度和动作时间）。当场景发生变化时，嵌入型直接搜索方法可以及时调整中等规模的行为，提高决策的适应性。更值得注意的是，修改后的actor能够匹配人类驾驶员的行为，宏观行为捕捉人类思维的跳跃，而中尺度行为优先通过驾驶技能进行调整。为了使agent能够适应不同类型的环形交叉口，本文设计任务表示方案来重构策略网络。在实验中，将算法效率和学习到的驾驶策略与包含宏观行为和恒定中尺度行为（期望加速度和动作时间）的决策进行了比较。为了考察该方法的适应性，本文对一种未经训练的环岛和两种以上的危险情况进行了仿真，以验证所提出的方法在不同的场景下相应地改变了决策。结果表明，所提出方法具有较高的算法效率和更好的系统性能。
关键词：决策、直接搜索、参数化、强化学习（RL）
1 引言
随着自动驾驶汽车的发展，决策方法在主动适应复杂、多变和交互式场景方面面临重大挑战[1]。除了感知技术的不确定性外，其他驾驶员的行为无法精确预测且受个人风格高度影响，这些因素限制了算法做出可信和主动的决策[2]。为了确保安全，当前的驾驶策略是保守的，有时与人类行为不同，这降低了驾驶策略的可接受程度。尽管智能车已经配备了L2或L3自动驾驶系统，但人类驾驶和机器驾驶的车辆在不久的将来仍需要混合使用[3]。因此，自动驾驶车辆的决策方法应在保证安全的情况下提高其可接受程度和性能[4]。
A. 最新技术回顾与挑战
下边回顾了有关决策和强化学习（RL）的文献，因为RL被认为是一种有利的选择，更适合决策方法之间的交互环境[5]
1）决策：相关研究采用基于规则和基于学习的方法对驾驶策略进行建模，如基于情景的状态机切换[6]–[8]、马尔可夫决策过程[9]–[12]等。相似之处在于，这些决定被定义为伴随着疲劳的特定的、离散的人类驾驶行为（如超车、车道保持、车道改变和右转弯） [13]。因此，决策需要由专家预先定义，并且很难推广到未重新定义的行为或场景[14]。此外，一旦驾驶场景变得复杂，尽管考虑了有限的驾驶行为，控制器仍需要执行复杂的切换规则来保证动作的安全可行[15]。
为了提高自动驾驶车辆的可扩展性，决策结合了更详细的信息，如横向和纵向目标[16]，动作空间在104左右离散化，作为巨大探索空间和更好概括之间的折衷。在[17]中，决策通过一些参数进行分解，这些参数是表示宏观和中尺度决策的物理量（比如末端相对横向位置和末端航向角），其价值最终形成了决策。由于这些参数涉及一个有限集，且每个参数都在特定范围内有界[18]，[19]，因此决策过程转化为寻找这些参数的最优值。基于参数的决策更适合于优化，并且增加了对多种场景的扩展性。
更值得注意的是，在自动驾驶车辆的分层控制框架下，通过联合设计决策模块和轨迹规划模块，并利用中尺度连续行为的信息，可以实现更好的性能[20]。
2）强化学习：无模型RL在连续问题中缺乏高效性和稳定性[21]–[24]。为了提高算法的效率和稳定性，一些文献提出了异步更新策略[25]、奖励重整[26]和预训练[27]、[28]等技术。当基于模型的控制器用于采样时，确定性策略方法具有更高的算法效率和稳定性[29]–[33]。
由于汽车控制问题的特殊性，当周围车辆的行为无法准确预测且可能突然改变时，必须密切关注变化场景[34]。在此期间，驾驶策略不同于正常情况，也不同于主智能体以前做出的决策，该决策只是暂时维持。因此，决策方法需要适应性，以便在可变和交互式场景中采取相应措施[35]。基于模型的方法可以有效地探索动作，驾驶策略可以快速迭代[36]。
B. 工作和贡献
在这项工作中，本文提出了一种优化嵌入式RL（OERL），以实现自动驾驶车辆在典型的可变交互场景环岛中的自适应决策。该方法同时确定宏观行为、末端相对横向位置、中等尺度行为、期望加速度和动作时间，其中人类驾驶员的期望加速度和动作时间不同，这在以前的研究中很少考虑。为了实现自适应决策，本文对Actor-Critic（AC）框架中的actor进行了以下改进。首先，在状态设计中，除了表征环境的状态向量（ER）外，还添加了表征任务的状态向量（TR）。其次，对策略网络进行重组，以平衡ER和TR的不同维度。第三，建立了一个神经网络经验模型，对轨迹规划模块的执行能力进行建模，并将其用于嵌入式优化方法。第四，直接搜索方法，即基于模型的优化方法，被用于对连续动作探索，以保证算法的高效性和在多变交互场景中的适应性。
本文的创新点和贡献可以概括如下：
1）该方法与驾驶员的驾驶行为相匹配。例如，在可变情景下，可以优先调整中等尺度行为，例如在达到脑海中设定的阈值之前，通过驾驶技能连续调整踏板和方向盘，然后转移到另一个宏观驾驶行为。此外，中等尺度的行为与人类驾驶员不同。
2）该方法合理地利用模型来提高了RL方法的效率。通过将基于模型的优化方法嵌入到RL中，与包含终端相对横向位置的离散宏观行为和期望加速度和动作时间的恒定中尺度行为的决策相比，该方法能够保证算法效率。
3）通过考虑TR和重组策略网络，驾驶策略可以及时识别不同工况并适应不同类型的环岛。
4）利用嵌入式优化方法，通过在线调整期望的加速度和动作时间，可以实现自适应决策，以避免交互场景中的紧急情况，并获得更好的性能。
本文的其余部分组织如下。在第二节中，首先描述了驾驶场景和整个系统。随后，提出了基于参数的决策问题。在第三节中，说明了OERL，其中包含一个改进的actor网络（AN）、直接搜索方法和一个神经网络经验模型。在第四节中，通过仿真评估了该方法的有效性。结论见第五节。
2 基于参数的决策问题描述
本节介绍了环形交叉口、一个复杂而典型的驾驶遭遇场景，并对整个控制系统进行描述。驾驶行为建模为马尔可夫决策过程（MDP）。由于该问题包含了行驶目的地确定和多车交互，因此状态空间被专门设计以使系统高效运行。在此基础上，建立了基于参数决策的动作空间。
A. 驾驶场景和系统描述
对于城市交通中的自动驾驶车辆，场景更加复杂，包含许多驾驶遭遇。除了根据导航完成的路径任务外，车辆还将与多个车辆交互并保持安全驾驶[37]。除了众多场景之外，环岛场景是一个典型复杂的驾驶遭遇场景，包含上述两种典型场景：行驶目的地确定和多车交互。环形交叉口的示意图如图1所示。在环岛上，当前车道和相邻车道上有多辆车辆。
图1 环岛和控制系统架构
非保守决策可以通过确定的和基于参数的描述来实现[16]，[17]。例如，在某些主动换道行为中，动作时间应较短，或加速度应较高。参数指相对于当前车道的末端相对横向偏移、动作时间和期望加速度，其中包含环形交叉口中的多种车道保持和车道改变。
在整体控制系统中，仿真环境在Prescan中建立，并在路径规划中确定车辆行驶目的地。然后，在基于参数的决策模块中，应用所提出的OERL来获取决策参数的值。然后，在轨迹规划和运动控制模块中，采用非线性模型预测控制直接优化轨迹。最后，运动控制变量输出到执行器控制模块。
B. MDPs 建模
在这项工作中，基于参数的决策问题被建模为RL中的MDPs。连续状态空间S、包含离散变量和连续变量的动作空间A以及奖励函数可设计为以下部分。
1）状态设计：不同的是，状态表示分为两部分：ER和TR。ER帮助agent做出安全决策，TR让agent完成路径任务。这一变化也与第Ⅲ-B节中引入的新AN一致。
关于ER，在环形交叉口中，周围车辆可分为两部分并进行编号，如图2所示。表1给出了不同位置的范围。一部分是靠近主车辆且应特别注意的车辆，其标记为浅蓝色，具有七个潜在位置（P1、P2、…、P7）。为了充分描述它们中的每一个，考虑了相对车道Ln（k）、相对速度vn（k）、加速度an（k）、相对距离dn（k）和周围车辆的意图In（k），其中下标n表示与特定车辆对应的潜在位置。
图2 决策场景示意图
表1 不同车辆的位置范围
这里，相对车道Ln（k）=Ln（k）− Lh（k）可通过周围车辆的当前车道Ln（k）和主车辆的当前车道 Lh（k）计算。相对速度vn（k）=vn（k）−vh（k）可通过周围车辆的速度vn（k）和主车辆的速度vh（k）计算得出。周围车辆的意图In（k）∈{−1，0，1}可以通过我们以前的工作进行预测。同时，人类驾驶员也会选择流畅的车道，而不是阻塞的车道。因此，将图2中用浅蓝色标记的相邻车道中的临近交通流（例如P8、P9、…、P12）考虑为ER的另一部分。此处，相邻车道前后的临近距离交通流状态可分别由标记区域内这些车辆之间的平均相对速度
和平均车头时距
。这里，THn，j（k）=dn，j（k）/vn，j（k）是编号为Pn的临近交通流中第j辆车的车头时距。因此，位置P1–P7中的状态向量可以表示为：
其中，Fn∈{1，0}表示位置（P1，…，P7）是否为可行车道。P8-P12位置的状态向量可以表示为：
因此，ER部分的状态向量可以表示为：
关于TR，在环形交叉口中，有一个带有路线规划的预期出口，其角度、半径和车道为αE，DE和LE。主体车辆和预期出口之间的相对纵向距离lh和车道Lh被作为TR的状态向量。此处，相对车道Lh（k）=LE−Lh（k）可通过出口车道LE和主车当前车道Lh（k）计算得出。相对纵向距离可表示为
式中，αh是主车和预期出口之间的相对角度，αh（k）和Dh（k）是k时刻主车的角度和半径。因此，TR部分的状态向量可以表示为：
最后，状态向量建立为S = (SER, STR)。
2）动作设计
当使用基于参数的决策框架时，可以得到更复杂的决策结果，该决策将应用于轨迹规划并改变[17]中的轨迹形式。因此，动作空间包含三个部分，可以表示为
其中，Ty（k）∈ {−L、0、L}是当前车道的横向目标偏移量，L是两条相邻车道线之间的距离。在该方法中，我们假设在时刻k时当前车道的终端相对横向偏移量与前方较短距离可以通过感知技术获取。atar（k）是目标加速度，ta（k）是预期的动作持续时间，其随着任务和工况的不同而变化。动作向量能够精确地描述决策，并且参数值随着决策不同而变化。更具体地说，表2列出了一些例子。车道变更场景中具有不同决策参数的决策可以描述为相同的人类行为，例如车道保持（加速、保持和减速），激进、中等和温和模式下的右侧车道变更（加速、保持和减速）和左侧车道变更（加速、保持和减速）。
3）回报设计
本文考虑安全回报rs、任务回报rt和执行回报re。在计算安全回报rs时，考虑当前车道前方 Lh(k) 和目标车道 Ltar(k)=Lh(k)+ sign(Ty(k)前方的周围车辆，其中也包含将在接下来5 秒内变换为这两条车道的周围车辆。当sign(Ty(k))=0时，只考虑位置 P4 的车辆。当主车换道，取sign(Ty(k))=-1;例如，位置P1、P2、P3和P4车辆将被考虑。假设对应位置Pn的车辆与其车道内的主车辆之间的距离为dn(k)。考虑到这些位置，安全回报rs的增量方程可以表示为
其中de=3是紧急距离，dc=1是碰撞距离。
任务回报rt可分为两类。一类与其位置一致，增量方程可以表示为：
另一类与动作一致。由于行驶在内车道在速度方面具有更多优势，因此主车倾向于驶入内车道。预期车道可大致计算为：
式中，αE和αlc是主车与出口的角度，以及对车道变化时角度变化的估计。然后，任务回报rt的增量方程可以表示为：
此外，当选择换道动作时，会比较前车和交通流。假设目标车道和当前车道中的车辆为P1和P4。奖励可以表示为：
相应的增量方程可以表示为
其中，k1=0.04、k2=0.03、k3=0.02和k4=0.1是系数。最后，执行奖励re可以计算为：
其中k5=0.01和k6=0.04是系数。LT是环形交叉口中的总车道。总奖励可以表示为：
3 优化嵌入式强化学习
在本节中，OERL在第Ⅲ-A节中进行了总结，其中对AC框架的actor进行了几次改进。然后，第Ⅲ-B——Ⅲ-D节详细介绍了这些改进。最终，所提出的方法提高了样本效率，并处理了变化的场景，这超出了纯学习方法。
A. RL算法设计与改进
在本文中，动作空间混合了离散动作和连续动作。为了获得与离散动作空间相同的采样效率，在RL中嵌入了基于模型的优化方法。由于决策过程没有物理模型，只有轨迹规划控制器才能提供一些先验知识，反映动作的执行情况。因此，可以建立一个经验模型来模拟主车的状态变化。之后，可以找到决策参数连续值的良好样本，这可以显著提高连续动作空间中的探索效率，加快学习过程。
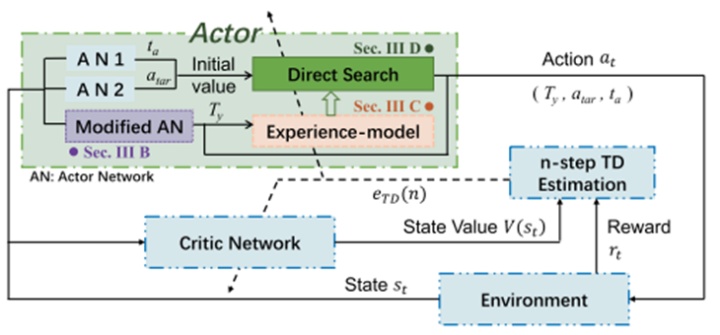
AC框架的示意图如图3所示。如下文所述，对AC框架的actor进行了改进。首先，对离散动作Ty的AN进行了修改，以有效地增强TR对动作的影响。其次，建立了三个神经网络经验模型来模拟所设计的轨迹规划控制器。然后，使用直接搜索法（单纯形搜索算法）指导搜索连续动作的参数值。
图3 AC框架及算法
OERL如算法1所示。根据算法1和图3可知，离散动作Ty由修改的AN决定。修改后的AN和critic网络的权重在一幕结束时更新，并从最后一个状态开始引导[25]。同时，AN1（AN1）和AN2（AN2）计算连续动作的初始点。AN1和AN2的权重通过基于经验模型的直接搜索计算得到的动作atar（k）、ta（k）利用监督学习进行更新。在每一幕中，更新一个有经验的好策略，将其与历史上最好的策略进行比较，并记录一个更好的策略。
B. Actor 网络
在决策中，任务特征（TR）与ER起着同等的作用。例如，在任务的初始阶段，agent有更多的自由选择更高的奖励动作，而在后期，它必须更多地考虑任务的成功。这将导致与ER不同决定。然而，TR只有两个维度，ER有52个维度。因此，当应用全连接神经网络时，TR将衰减。当这两种表示具有显著不同的维数时，会给函数逼近带来很大困难。
在这项工作中，改变了AN中关于终端相对横向偏移Ty的结构，如图4所示。它有两个隐藏层。为了有效地保留此功能和行为，复制TR，并将这些向量重新放入输入层和第一个隐藏层。因此，在输入层中有104个节点，其中一半是状态表示，另一半是复制TR。在第一隐藏层中，常规节点为32个。复制TR以形成相等的32个节点，以重新放入第一个隐藏层。第二个隐藏层只有常规节点，数量为16。
图4 决策和轨迹规划架构
C. 神经网络经验模型
建立神经网络经验模型，利用BP神经网络对多个运动点进行学习从而模拟不同决策参数下主车的状态变化。
首先，收集轨迹数据。由于决策参数的值在一个固定的范围内，为了获得其在不同决策中的执行情况，进行了若干并行实验。在参数决策D=（ta，atar）下设计的轨迹规划控制器可以表示为：
其中x=[X，Y，φ，vx，vy，ωr]是状态向量；u=[a，δf]是控制向量，a改变纵向速度vx；考虑了一个关于纵向速度vx变化的简单方程；并设计了一个下层跟踪控制器来跟踪期望的a，这简化了运动控制模型。P（ta）=（X（ta），Y（ta））是预测时域的终端位置。Rac和Rcd分别为直线路段和曲线路段。运动控制模型
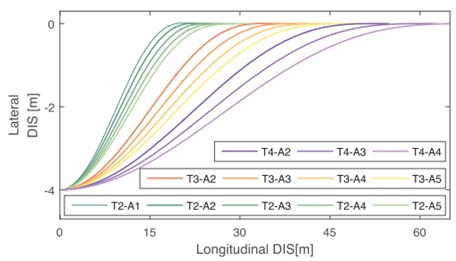
附在附录中。在并行实验中，当Ty=0且期望加速度为atar∈ [−2,2]时，期望的决策参数动作持续时间ta∈ [2,4]。不同决策D=（ta，atar）下的优化轨迹可作为数据库，其中部分如图5所示。如图5所示，中等尺度变量，如预期加速度atar和动作持续时间ta，对自动驾驶车辆的轨迹有重要影响。
图5 不同决策参数组合下的车辆轨迹。其中，T2,T3和T4指ta=2,3,4;A1-A5指atar=-2,-1,0,1,2
图6 轨迹示例
然后，每个轨迹可以用系数lx表示，横向运动系数ly，1，ly，2，…，ly，5和时间系数lt，1，lt，2，…，lt，5。我们以其中一条轨迹为例，图6表示该轨迹的特征。在一个轨迹中，lx可以表示为：
式中，sx是纵向位移，vh，0是主车的初始速度。同时，系数lx也会受到期望加速度atar的影响。在横向运动中，记录该轨迹上的五个点，其中纵向位移分别为1/8lx、1/4lx、1/2lx、3/4lx和7/8lx。相应的横向运动系数ly，i和时间系数lt，i可表示为:
最后，系数lx，横向运动系数序列ly，1，ly，2，…，ly，5和时间系数lt，1，lt，2，…，lt，5通过三种神经网络为经验模型进行学习，这能够反映各种轨迹规划的特点。输入向量包含主车的初始速度vh、0、预期加速度atar和预期行动持续时间ta。
为了避免学习过程中出现局部极小值，遗传算法将Levenberg–Marquardt训练方法与BP神经网络相结合。所有的神经网络经验模型都有两个隐层，第一层和第二层分别有128个节点和64个节点。训练集和测试集的样本数分别为322和18。平均训练步数约为500，这将随初始权重的不同而变化。训练误差的阈值为1e−6.当主车速度vh,0=10 m/s2时，神经网络经验模型训练结果如图7所示。
图7 神经网络经验模型输出结果
D.利用经验模型直接搜索连续动作
该优化算法利用神经网络模型和周围车辆的运动预测来寻找最优期望加速度atar和期望动作持续时间ta。此处将不详细讨论对周围车辆运动的预测。由于数学模型被神经网络经验模型所取代，其保留了轨迹规划的特点，因此无法利用梯度来优化决策参数。直接搜索方法完全依赖于目标函数值，并用估计的梯度替换实际梯度。在连续动作空间的RL中，算法的效率与动作探索一致。一旦能够探索出好的动作，算法的效率就会显著提高。在这项工作中，单纯形搜索法，内尔德均值法，用于优化决策参数。利用上述神经网络经验模型，可获得纵向位移系数lx、时间步长序列Ts以及主车纵向位移为Sx时的横向位移Sy，其可表示为：
上式中，sx由（16）计算，横向运动系数ly，1，ly，2，…，ly，5和时间系数lt，1，lt，2，…，lt，5由（17）计算得出。
然后，选择当前车道（Ln=Lh）和目标车道（Lh+sign（Ty）=Ln）中的车辆。当决策Ty=0时，主要考虑位置P4或P9处最近车辆，期望动作持续时间ta设置为1秒。目标加速度atar经过优化，以保持主车和前车的时距。当判定Ty ≠0时，取Ty=L，例如，处于位置P4且d4<2de的车辆。考虑位置P1、P2和P3中|di|<2de的车辆，并优化期望行动持续时间ta和期望加速度atar，以尽可能保持主车和前车之间的距离。周围车辆的轨迹被生成，周围车辆Pn在时间序列Ts的j步中的位置可以预测为（sn，x（Ts（j）），sn，y（Ts（j））。这里，sn，x和sn，y的序列分别表示为Sn，x和Sn，y。意图和轨迹预测的准确性没有讨论，这已经有很多以前的工作。因此，目标函数是增量计算的，可以扩展：
此外，在目标函数的增量方程中还考虑了期望动作持续时间ta和期望加速度atar，即
利用神经网络经验模型和单纯形直接搜索法，可以找到决策组合D=（ta，atar）。有效的动作探索可以大大提高。同时，在连续RL中，策略被神经网络逼近。因此，经过训练的策略可以依次提供良好的初始单纯形顶点，这将影响直接搜索方法中的迭代次数。
4 复杂驾驶场景下的仿真结果
首先，对直接搜索法中的一些参数进行了评估，并对其学习效率进行了比较。然后，在并行仿真中展示了所学习的决策策略，并与固定的换道时间和没有纵向速度变化的情况进行了比较。最后，对一种未经训练的环形交叉口和另外两种危险情况下的性能进行了仿真，以进一步评估所提方法的适应性。
A.学习阶段评估
在这项工作中，我们使用直接搜索法来获得混合动作空间中的连续动作，这可以大大提高算法效率。
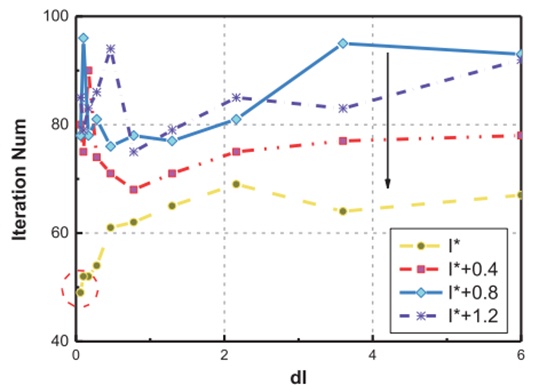
首先，评估了直接搜索方法的有效性。设计初始单纯形IS=（I−di，I，I+di）中的初始点I和步骤dI是实验中的影响因素。这里，初始点I是由ANs1和2输出的（atar，ta）。步骤dI是初始点I的变化。当初始点以不同的步骤dI接近最优点I时，记录迭代步骤。如图8所示，更接近最优点的初始点I具有更少的迭代步骤。此外，在适当范围内选择的不同步骤dI对迭代次数几乎没有影响。因此，AN输出初始点I，其将在学习过程中更新，并且手动设置步骤dI。
图8 不同影响因素下的对比结果
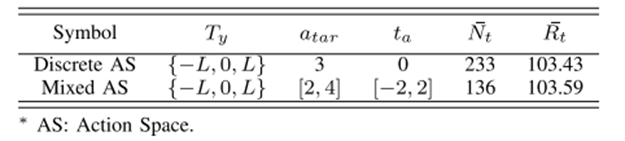
在这项工作中，直接搜索方法可以在连续动作空间中提供良好的样本，并与离散动作学习获得相似的算法效率。在训练阶段，由于连续动作空间中的算法样本效率很低，我们只比较了混合动作空间中的学习和离散动作空间中的正常学习的学习效果。在离散动作空间问题中，目标加速度和预期动作持续时间设置为常数，如表Ⅲ所示。进行了几个平行实验，记录了整个训练过程Nt。
计算了平均训练时间和平均奖励，如表三所示。在表三中，样本效率在这两种学习中具有相似的趋势，即所提出的学习方法可以实现更精细的决策并获得更高的奖励。同时，将基于规则框架的AN与重构后的AN进行比较。在重构AN中，隐藏层中的节点数分别为32和16。在常规AN中，隐藏层中的节点数分别为64和32。一个规则框架的训练迭代次数大约是重构后的三倍，结构也要复杂得多。
表3 离散和混合动作空间结果比较
B.驾驶策略评估
图9 场景N1与N2的仿真结果
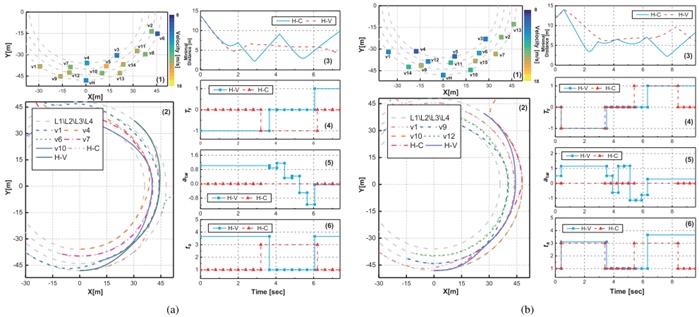
首先，驾驶策略学习的仿真结果如图9（a）和（b）所示。在仿真中，我们假设可以精确预测周围车辆的意图。利用已知的高精度车辆意图和运动学模型对轨迹进行预测。未准确预测周围车辆意图的情况将在第IV-C节中讨论。如图1环岛示意图所示，根据路线规划，主车在入口E1进入，在出口E3退出。在每个场景中，将学习到的驾驶策略与包含终端位置的离散宏观行为和包含加速度及动作时间的恒定微观行为的决策进行比较。
在场景N1中有15辆车，初始位置和速度如图9（a）的子图（1）所示。当前车道上有一辆周车v10，内车道上没有其他周围车辆。因此，主车将切换到内车道，并当接近入口E3时切换至外车道。在不同决策参数和恒定决策参数下，总仿真时间分别为9.97和11.6秒。图9（a）的子图（2）显示了部分周车的轨迹轮廓。周车和主车在不同决策参数和恒定决策参数下的轨迹轮廓（如表三所示）在图9（a）的子图（2）呈现。与周车的最小距离如图9（a）的子图（3）所示。决策动作参数如图9（a）的子图（4）-（6）所示。从这些子图中可以看出，这两种决策方法导致环形交叉口中不同的车道变换时间，以及不同的期望加速度atar和期望动作持续时间ta。采用可变参数决策的车辆可以在较短的时间内顺利执行内车道的换道并通过环岛。
在方案N2中，同样对上述内容进行比较。如图9（b）的子图（1）所示，周车v10在当前车道的内车道上行驶，且与当前车道上周车的距离大于内车道。具有可变参数决策的主车将加速和延长换道动作时间，以实现换道，而不是像具有恒定参数决策的主车那样保持车道。同时，在此过程中，与周围其他车辆的最小距离保持在安全的情况下。在变化的决策参数和恒定的决策参数下，总模拟时间分别为9.7和12.0秒。
在场景T1中，测试未经训练的完全不同的环岛场景。环岛仅有三条车道，主车需要在E1和E3中进出。半径比原始环岛小得多，原始环岛分别为33米、29米和25米。如图10的子图（4）-（6）所示，在进入内部车道后，主车仅在两个时间步长内保持车道，然后转向外部车道以退出环岛。
图10 场景T1仿真结果
在这些仿真中，我们可以看到，主车已经学习了主动驾驶策略，这表明在没有潜在危险情况下主车将尝试超车。
C.交互式场景评估
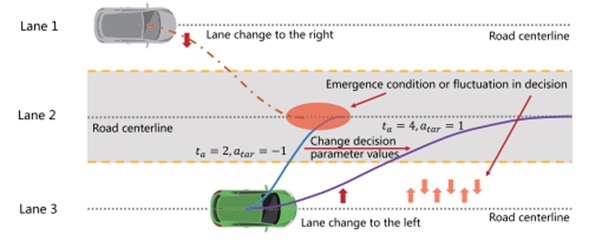
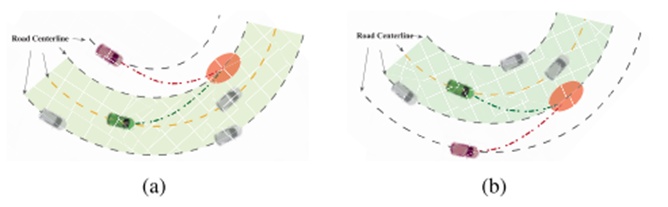
如图11所示，可能会出现一些更复杂和危险的场景。当主车改变车道时，下一个相邻车道上的周围车辆（灰色车辆）也可能改变到目标车道，并导致情况或决策波动的出现。造成这种危险情况可能有以下原因。首先，意图无法准确预测且可能会突然改变。如果无法正确预测周车的运动，主车决策的改变最终导致波动，甚至造成危险。如第II-B节所示，下一相邻车道的周围车辆实际上不在决策对应区域（浅绿色区域，如图12所示）。该区域内的周车很难被察觉，在正常决策中不被考虑，但也会引起波动甚至危险。此外，盲目扩大决策区域会增加问题的复杂性，不利于决策的合理性。
图11 复杂危险场景示意图
图12 环岛中两个复杂危险场景实例（（a）为左换道E1，（b）为右换道E2）
基于上述两个主要原因，本文提出的方法还有另外两个优点，可以进一步提高决策过程的安全性和稳定性。首先，如图5所示，决策参数会影响计划轨迹。一旦下一个相邻车道上的周车将车道更改为与主车相同的目标车道，不同的决策参数可用于改变轨迹形式，并与周围其他车辆保持安全距离。同时，直接搜索法可以及时地给出这种特定情况下决策参数的最优值。因此，主车可以首先根据当前决策相应地调整以适应多变的环境，并做出尽可能小的改变。这样，主车可以临时更改驾驶策略。除非安全受到很大影响，否则主车将不考虑其他类型的决策。
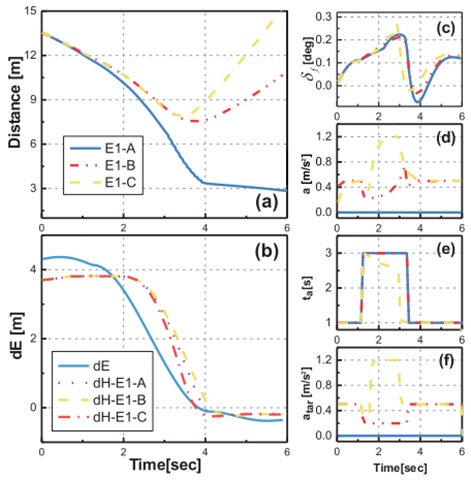
我们展示了在两种情况下发生这种情况时的结果，如图12所示。在每种情况下，进行了三个比较实验：固定决策（A:−L,3,0），考虑红色车辆时，原始驾驶策略不变（B），考虑红色车辆时，决策及时变化（C）。用于评估安全性的两辆车之间的距离、主车（dH）和红色车（dE）到目标车道的距离、控制变量、转向角δ、目标加速度a、优化结果、预期行动持续时间ta和目标加速度atar如图13和14所示。从结果中可以看出，考虑到红色车辆（C），当决策及时改变时，控制距离以保证安全（a），而不会引起控制（c）-（f）的波动。此外，这也有助于主车增加获得优先通行权（b）的可能性，从而缩短转向目标车道的时间。
图13 场景E1结果对比
图14 场景E2结果对比
5 总结
在本文中，所提出的OERL实现了自适应决策，并在一个典型的可变交互场景——环岛中进行了验证。改进后的方法匹配了驾驶员行为，实现了自适应决策，显著提高了算法效率。相应地，actor的状态、动作和框架以及策略网络都是专门设计的。通过实验验证了该方法在保留连续变化的中尺度行为的情况下取得了较好的性能，同时与包含终端位置的离散宏观行为和加速度和动作时间的恒定微观行为的决策具有相当的样本效率。该方法除了具有较高的采样效率外，还可以使驾驶策略快速适应不同类型的环行交叉口和多变的场景，从而确保安全性。
在我们未来的工作中，我们将研究该方法在多个场景下的扩展。将更精确地考虑其他交通参与者的预测，以提高控制系统的安全性。
附录——非线性运动控制模型
在轨迹规划控制器中，使用了非线性运动控制模型[17]。该模型包含同时考虑纵向和横向动力学的非线性车辆模型以及运动学方程。在考虑纵向动力学的情况下，考虑纵向速度变化时，将单轨车辆动力学模型转化为非线性车辆模型进行模型预测控制。这里，考虑后轮驱动、前轮转向的车辆。在全局坐标系中，考虑车辆运动学的几何关系，建立非线性运动控制模型，如下所示：
x=[X，Y，φ，vx，vy，ωr]是状态向量；u=[a，δf]是控制向量。考虑了一个简单的纵向速度vx变化方程，设计了一个低阶跟踪控制器来跟踪期望的a，这简化了运动控制模型。δf是方向盘转角。X和Y是全局坐标系中X和Y方向的坐标；φ是全球坐标系中的航向角；M是车辆的质量；vy为横向速度；ωr是横摆率；Iz是车辆绕z轴的转动惯量；lf和lr分别是重心（CoG）到前轴和后轴的距离。考虑一个简洁的轮胎模型，前轮αf和后轮αr中的轮胎侧偏力可以线性化，因为侧偏角很小，并且前轮和每个后轮上的轮胎侧向力Fyf和Fyr可以写成：
式中，Cr和Cf分别为前后轮胎的侧偏刚度。
参考文献
广告
广告
编辑推荐
最新资讯
-
厂商要多努力，才能让用户听起来毫不费力？
2024-11-22 17:10
-
TOP30！海克斯康入选2024福布斯中国数字科
2024-11-22 15:25
-
揭秘国产装备制造厂商的成功秘籍：好耐电子
2024-11-22 15:24
-
一文详解安全分析方法STPA：以自动紧急制动
2024-11-22 15:20
-
选对涉氢压力表：守护涉氢场所安全的关键一
2024-11-22 15:19
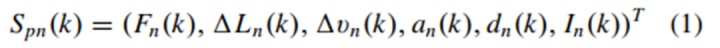
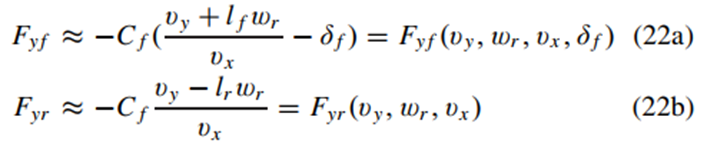
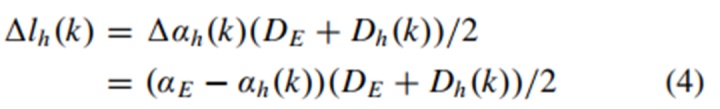
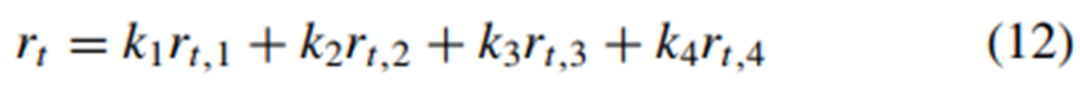
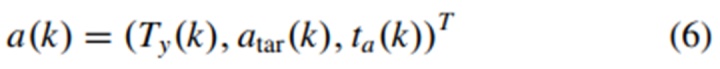
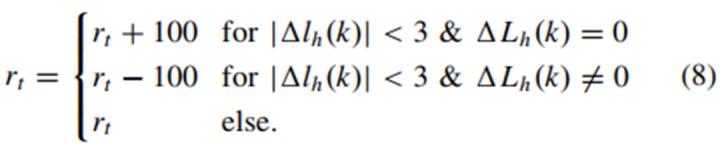
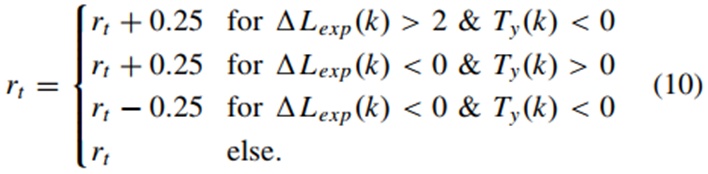
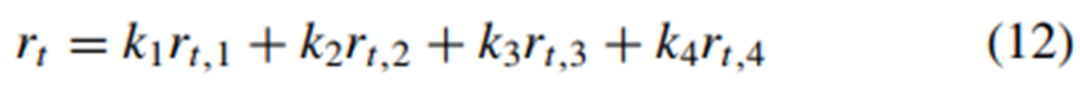
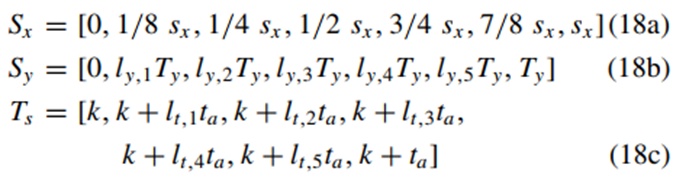
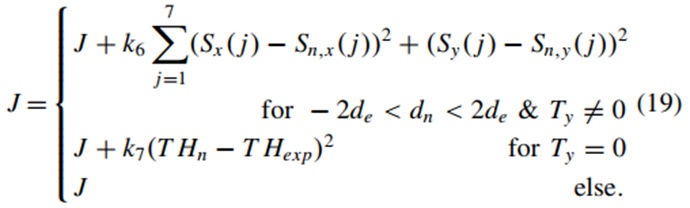
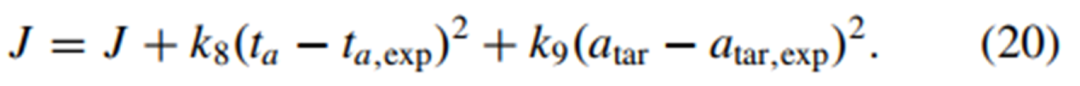
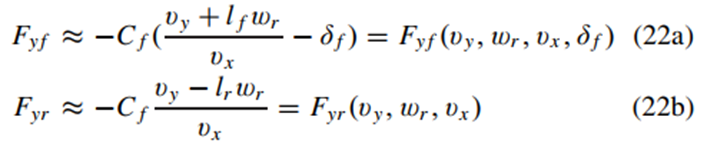
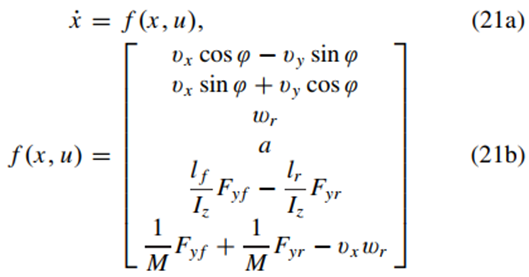
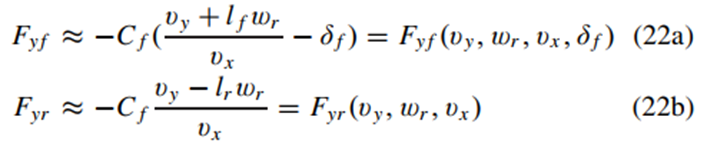
广告
广告
