广告
基于热-结构耦合的盘式制动器磨损状态下制动噪声研究
2021-11-02 21:37:18· 来源：汽车NVH之家
摘要：为了研究在工作状态下制动器摩擦片发生磨损后的制动噪音问题，建立了均匀磨损和不均匀磨损两种有限元模型。通过热-结构耦合模块的仿真分析，得到均匀磨损
摘要：为了研究在工作状态下制动器摩擦片发生磨损后的制动噪音问题，建立了均匀磨损和不均匀磨损两种有限元模型。通过热-结构耦合模块的仿真分析，得到均匀磨损和不均匀磨损两种状态在不同磨损量时的模态分布与振型，求出了各阶固有频率。采用复特征值法求出了系统不稳定模态下的不稳定系数。研究结果表明，两种磨损状态均对制动器系统的稳定性有一定影响，随着磨损量的增大，制动器的固有频率呈下降趋势，均匀磨损状态下不稳定模态的数值略有增加，不均匀磨损状态下不稳定模态的数值上升趋势明显，发生制动噪声的倾向显著增加。通过分析不均匀磨损产生的原因，提出了相应的改进方法，为制动器系统的进一步优化提供了理论依据。
随着人们生活水平的不断提高，汽车作为日常交通工具，其安全性与平顺性作为行驶品质的标准也越来越受到汽车生产商与乘客的重视。制动器作为汽车不可缺少的零部件，通过自身制动盘与摩擦片的接触产生摩擦阻力来控制车辆的行驶速度，以保证汽车的行驶安全，而伴随着制动所产生的摩擦颤噪成为了影响驾驶安全与乘坐舒适性的一大难题。现在市场上广泛使用且较为成熟的汽车制动装置的结构形式主要有盘式与鼓式两种，其中盘式结构的制动器具有机构简单、利于散热、可靠性强、便于安装维修等优点，已成为现代家用轿车的主流形式。
制动器在长时间使用后会发生较为严重的磨损现象，理想状态下，受到均布载荷作用的摩擦片与制动盘之间的磨损是均匀分布的，但在实际运行中制动过程伴随着摩擦热的产生，而摩擦接触区域不同位置的散热条件不同，导致摩擦片制动过程中温度场的分布是非均匀的，进而导致接触区域不同部位的应力不同，出现偏磨现象。在针对偏磨这种不均匀磨损现象的研究中，陈东等通过ABAQUS有限元软件采用热-结构直接耦合的方法计算了紧急制动过程中摩擦片在不同时刻温度与接触压力的分布，并通过分析得到了新摩擦片工作的前期会发生切向偏磨，而偏磨达到一定程度时，摩擦片因自身形态的改变会影响偏磨的位置，使得摩擦的接触面趋于均匀，故可将摩擦片的磨损看作是一个自适应调节的过程。张方宇等则研究了制动器热应力耦合状态下磨损量的数值计算方法，并利用有限元软件模拟了快速制动过程中热应力耦合作用下摩擦片的磨损过程。现有文献中对于已产生磨损的制动器在摩擦生热状态下制动器系统的噪声问题未做深入研究，本文旨在通过热-结构耦合的方式，针对实际工况下因摩擦热而产生大幅温升的制动器在两种不同磨损状态下的制动噪声问题进行分析研究，为制动系统的深层次优化提供理论依据。
1 制动噪声的产生机理
汽车制动是通过摩擦力来阻滞安装在轮轴上制动盘的旋转运动来实现的，而这个摩擦阻力是制动盘与受压摩擦片相接触而产生的。制动摩擦力以及制动部件形态的变化会导致自激振动，并产生噪声。关于振动噪声产生机理的研究中，较为成熟的理论有：①黏性滑动理论。当接触表面的动摩擦系数与静摩擦系数不一致时，不断变化的摩擦力将自激振动产生的能量源源不断地引入系统，造成其稳定性下降，产生制动尖叫的现象。②模态耦合理论。当制动器工作时，如果存在具有相似特征的模态发生耦合，制动系统将发生共振并引发制动尖叫。研究表明，由于制动盘转速和温度变化等因素的影响，制动器的摩擦系数下降，出现黏滞滑移现象，使得各部件的振动幅度相互叠加，导致共振，同时向周围辐射振动能量而形成噪声。一般来说，制动噪声来源于刚度较小的摩擦片，该摩擦片同时会带动运转中的制动盘而产生噪声。
根据振动频率的不同，制动噪声可分为以下3种：①频率在100～1 000 Hz之间的低频噪音，声音较为低沉；②频率在1 000～7 000 Hz之间的低频尖叫，由转动盘的面外模态与摩擦片的弯曲模态耦合产生，噪声刺耳；③频率在7 000 Hz以上的尖锐刺耳的高频尖叫盘，由转动盘面内模态之间相互耦合产生。通过解析振动方程的复特征值可求解制动噪声的发生频率，针对计算量较大的复杂模型，可通过复模态求解得出，得到系统各阶模态中的不稳定模态及其各部件的共振频率。
2 盘式制动器模态与不稳定系数分析理论
采用盘式制动时，振动模态是引发噪声的主要因素。通过对系统的模态分析求解物体的固有频率和振型，进而可以解决系统自激振动问题。相关动力学方程为：
(1)
式中：M为物体质量矩阵；C为物体阻尼矩阵；K为系统刚度矩阵；
为节点加速度矢量；
为节点速度矢量；u为节点位移矢量；F(t)为系统受到的时变载荷函数。
因阻尼对系统模态的影响较小，在模态分析中可以忽略。通过有限元分析软件中的静态结构分析模块，以模型的初始状态为依据，设置载荷与接触关系，能够进行预应力模态分析。为了简化计算，可以将阻尼忽略。设载荷函数F(t)=0，则系统在自由振动状态下的方程为：
(2)
对式(2)可采取直接积分法或模态叠加法来求解，其中模态叠加法因原理更贴近应用中的情况，故其应用频率高于直接积分法。模态叠加法通过将系统各部件固有频率与其主要模态耦合的通用数学方程转化为非耦合的独立方程来求解。在M矩阵和K矩阵均为常数的线性振动系统中，自由振动的形式为如下的简谐振动：
{u}={φ}icosωit (3)
忽略阻尼条件，以基本特征值算法求解振动方程：
(4)
式中：[K]为刚度矩阵；[M]为质量矩阵；{φ}i为特征向量，代表第i阶自由振动频率下的振型；ωi为i阶自振角频率，代表第i阶模态的固定频率，即特征值。
自由振动频率fi=ωi/2π(5)
制动时，摩擦力在系统内产生耦合作用，此时的运动方程为：
(6)
式中：μ是制动器系统的摩擦因数。
由式(6)分析可知，若摩擦力引起系统耦合，使得刚度矩阵不对称，则对应的特征矩阵不对称，从数学角度看，在一定条件下，不对称矩阵特征值的形式为复数。
系统的特征值即为系统模态频率，由控制理论得知，系统的复特征值的实部为负时，该系统为稳定系统；反之，当复特征值的实部为正时，该系统不稳定。因此，在对制动器的工作状态求解时，若模态复特征值的实部为正，则为不稳定模态，其工程表现为有噪声倾向。故对制动系统复模态求解即可实现对噪声的预测。
式(6)的特征方程为：
det(s2M+sC+K+μKf )=0 (7)
s=σ+jω (8)
式中：s为系统复特征值；σ为特征值实部，也是系统的阻尼系数；ω为特征值虚部，也是系统的自然频率。
为衡量系统某阶模态的不稳定程度，将复模态的阻尼比ζ定义为：
(9)
式(9)中的负号表示负阻尼，将模态不稳定系数γ标记为：
(10)
若系统的某阶复模态存在负阻尼，阻尼比为负数，则表示在此阶模态下，阻尼不仅不消耗能量，反而向系统中反馈新的能量，从而引发自激振动，故其为不稳定模态。实际工况下，一般用不稳定系数γ的值来区别不稳定模态，当γ>0.01时，视为不稳定模态；反之，当γ<0.01时，则视为稳定模态。
3 盘式制动器热-结构耦合模型
由于制动过程会产生大量的热，采用热-结构耦合分析法更符合真实工况。本文拟根据制动器模型在不同时刻的热流密度求得制动器在不同时刻的温度及热应力，然后通过热应力与结构应力的耦合分析，求得该模型的前30阶自然频率以及相应振型图，并根据其复特征值结果得到该系统的不稳定模态，为进一步的优化提供参考依据。
3.1 制动器摩擦热流密度
所研究摩擦片的外径为308 mm，内径为220 mm，包角为60°，制动过程中制动盘的初始速度为114 rad/s，均匀磨损状态下施加在摩擦片上的制动压力为5 MPa，不均匀磨损状态下制动压力为8 MPa，两种状态下制动时间均为2 s。假定制动过程中产生的所有热量均被制动盘和摩擦片所吸收，则摩擦接触在一个微小面积dA上产生的热量为：
dQ=ημp(t)ω(t)rdAdt (11)
式中：η为零部件得到摩擦生热量的比例；μ为摩擦系数；p(t)为零部件所受到的法向压力；ω(t)为转动盘的角速度；r为摩擦半径。
制动盘摩擦的热流密度q(r,t)为：
(12)
制动盘与摩擦片的热流分配比例kq为：
(13)
式中：qd(r,t)为制动盘的热流密度；qp(r,t)为摩擦片的热流密度；ρd、ρp分别为制动盘、摩擦片的密度；cd、cp分别为制动盘、摩擦片的比热容；λd、λp分别为制动盘、摩擦片的导热系数。
代入上述模型参数，可求得均匀磨损状态下的摩擦热流密度q1为：
q1=1.23-0.615t (14)
不均匀磨损状态下的摩擦热流密度q2为：
q2=1.48-0.74t (15)
3.2 仿真模型的分析与简化
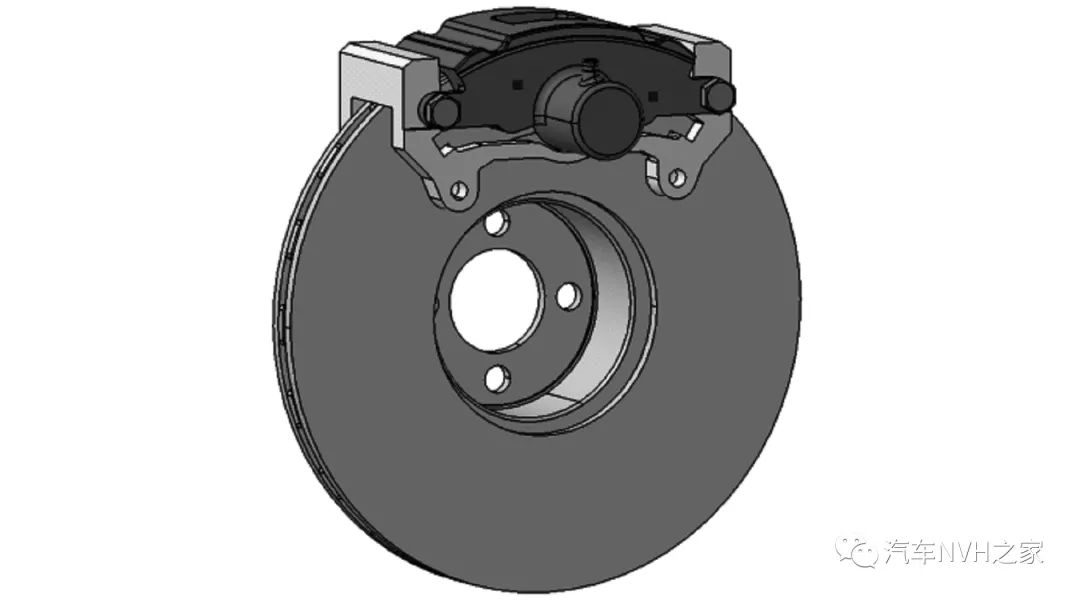
图1所示为浮钳盘式制动器的实物图，主要由制动盘、摩擦片、制动钳、液压缸与活塞等部分组成。图2 所示为制动器工作原理图。当刹车踏板被踩下时，刹车总泵受到连杆的推力作用，将液体压力通过液压缸传递到活塞，推动活塞和与其相连的摩擦衬块向刹车盘方向运动，当活塞侧摩擦衬块接触刹车盘时，刹车卡钳在液压缸内压力的作用下向活塞运动的反方向运动，从而使两块摩擦片对刹车盘形成合夹，在摩擦力的作用下使车速降低。
图1 制动器实物图
图2 制动器工作原理图
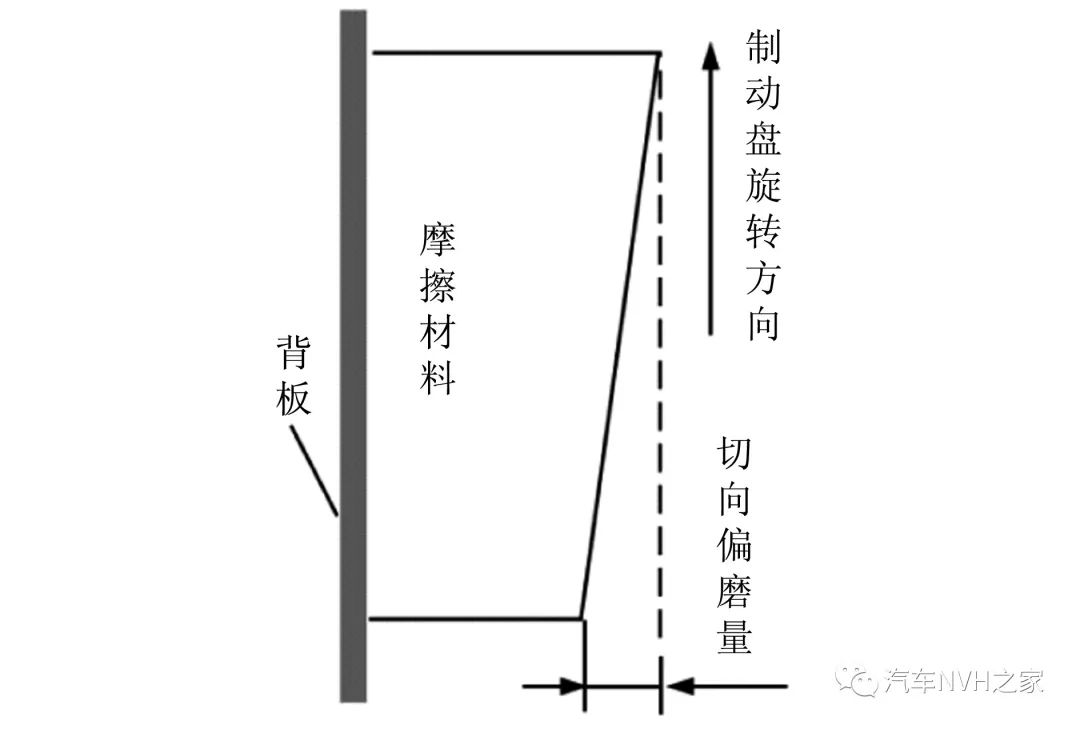
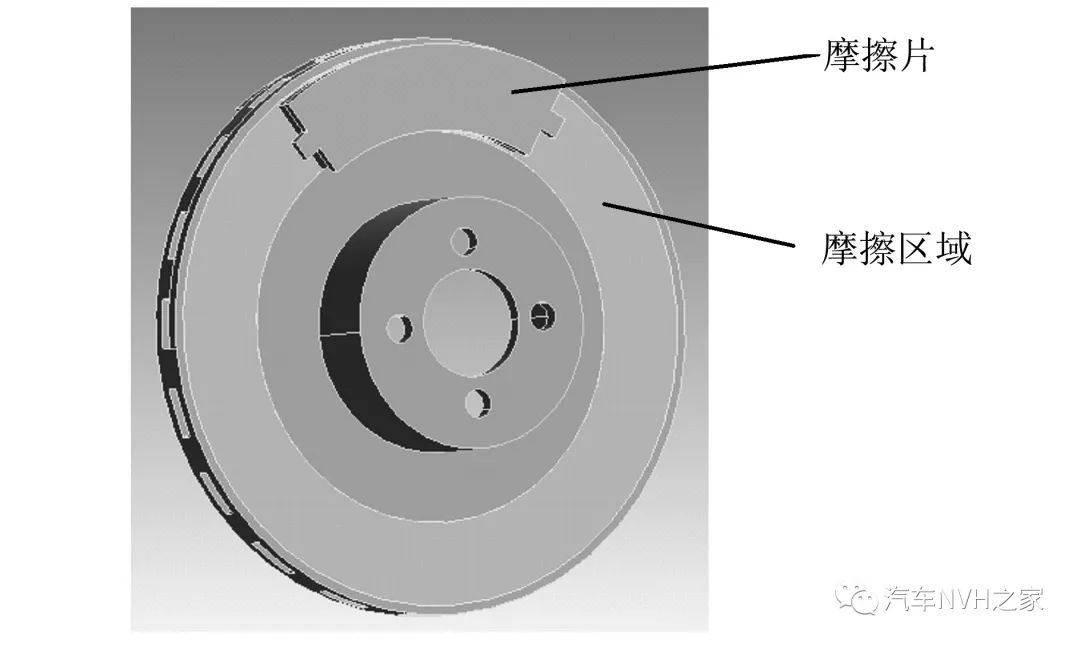
图3所示为某型号轿车制动器的三维模型。噪声主要来自于制动盘与摩擦片，为了减少计算量，提高效率，本文将装配模型简化处理，保留去掉倒角和圆角后的制动盘体和两侧摩擦片。制动盘外圆直径330 mm,内圆直径150 mm，厚24 mm。制动盘的通风孔厚8 mm，分布在制动盘轴向的中心区域，每个通风孔的包角为10°，每个加强肋的包角为8°。整个制动盘共20个通风孔与加强肋。摩擦片外侧直径为308 mm，内侧直径为220 mm，包角为60°，制动盘与摩擦片的材料物理性能分别见表1、表2和表3所示。新摩擦片的厚度为14 mm，长期使用后产生切向偏磨的摩擦片的截面形状如图4所示。为研究不同磨损状态下的制动噪声情况，设置了6组仿真工况。均匀磨损摩擦片的厚度分别为14 mm、11 mm、8 mm，不均匀磨损的偏磨量分别为在其对应的均匀磨损基础上偏磨1.5 mm。工况分组如表4所示。
图3 某型号制动器三维图
表1 制动盘材料HT250的物理性能
表2 摩擦片材料的物理性能
表3 温度对摩擦片材料性能参数的影响
图4 摩擦片切向偏磨示意图
表4 不同厚度摩擦片工况分组 单位：mm
3.3 盘式制动器典型结构的建立与网格划分
为了研究盘式制动器的热-结构耦合状态，本文采用ANSYS软件进行仿真分析，在Engineering Data中添加仿真用到的两种材料，然后将制动器的简化模型加入Geometry模块中并对其表面进行分割。图5所示圆环为制动时的摩擦区域。将制动部件划分为图6 所示的网格，且网格尺寸为6 mm，可得到82 271个网格，140 349个节点。制动盘与摩擦片为摩擦接触，均匀磨损状态下制动压力取5 MPa，不均匀磨损状态下制动压力取8 MPa。将热流密度分别赋予制动盘两侧的摩擦区域，求得制动过程中不同时刻不同位置温度场的变化，可实现热应力与结构应力的耦合分析。
图5 简化处理后的制动器模型
图6 网格结构示意图
4 磨损状态下制动噪声的分析
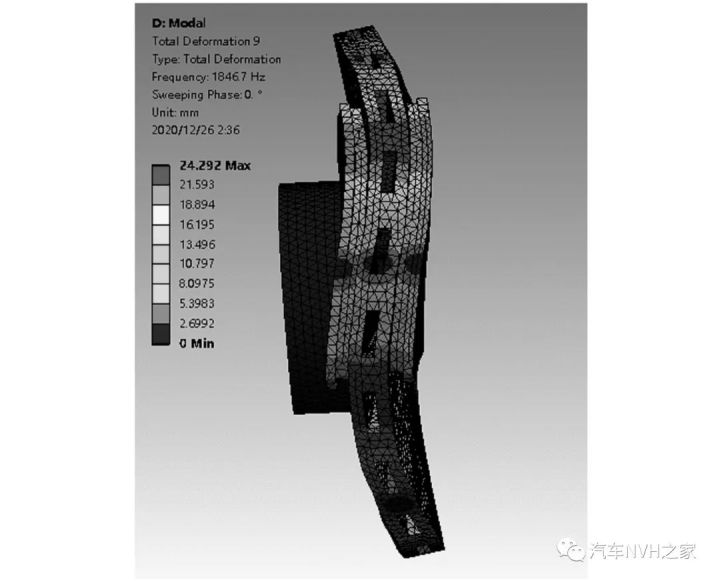
对6组工况进行仿真模拟，得到了不同磨损状态下制动器的固有频率和不稳定系数。制动器典型不稳定模态的云图如图7所示。仿真求得的各阶固有频率与不稳定系数分别如图8和图9所示。
(a) 制动器正面云图
(b) 制动器侧面云图图7 制动器典型不稳定模态仿真图
(a) 均匀磨损状态
(b) 不均匀磨损状态
图8 不同磨损状态下制动器各阶固有频率分布图
(a) 均匀磨损状态
(b) 不均匀磨损状态
图9 模态不稳定系数分布
4.1 不同磨损状态下固有频率分布
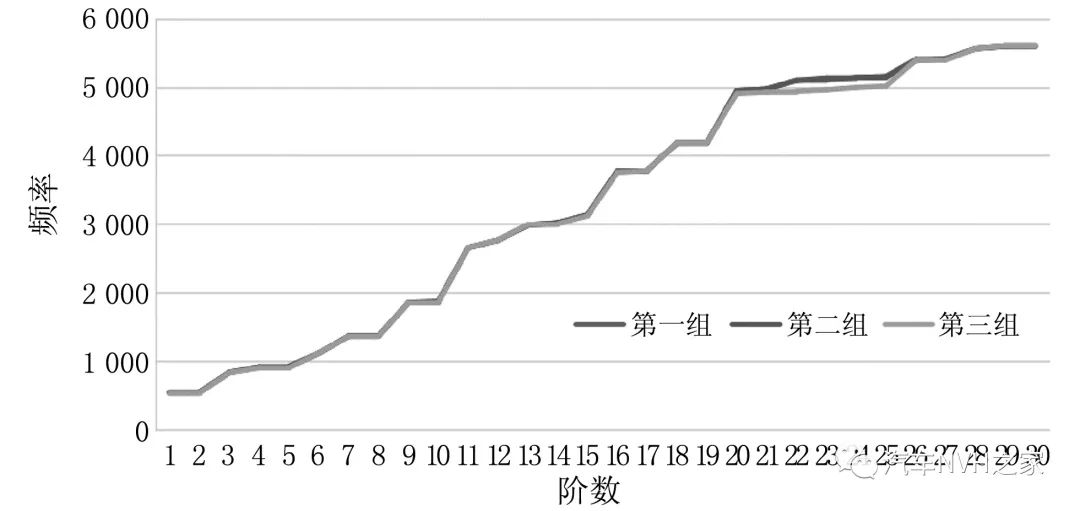
由图8(a)可看出，3组仿真值高度重合，均匀分布在500～5 700 Hz之间。第一组的各阶固有频率略大于后两组，第二组居中，第三组最小，所以随着均匀磨损的深入，摩擦片的厚度减少，固有频率也随之降低，但是磨损量的变化对制动器固有频率的影响不大。
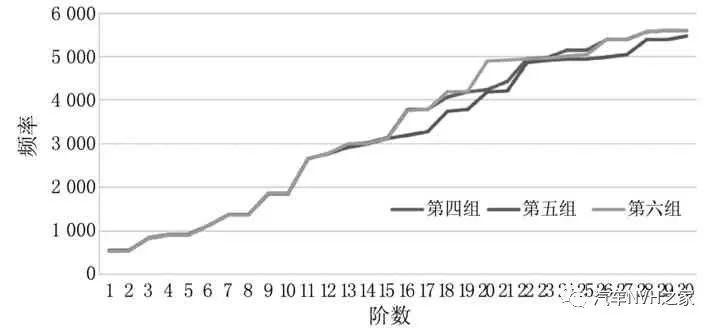
由图8(b)可看出，与前3组类似，在不均匀磨损状态下，制动器的固有频率依然均匀地分布在500～5 800 Hz之间，其前15阶频率高度重合，分布于500～3 000 Hz之间，其值随着磨损量的增加而略有减小，而后15阶频率则出现较大的波动，其中第四组和第六组明显高于第五组，当摩擦片厚度为11 mm，偏磨量为1.5 mm时，制动器的固有频率最低，3组仿真的频率在波动之后重新收敛，第30阶频率接近于5 500 Hz，相差100 Hz。因此，不均匀磨损状态下磨损量的变化对制动器固有频率的影响不大。
4.2 不同磨损状态下模态不稳定系数的分布
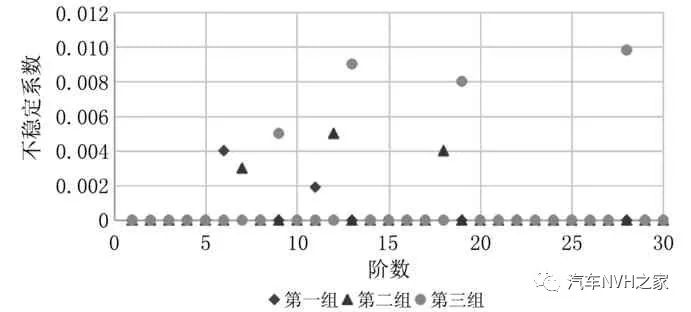
由图9(a)可看出，第一组仿真结果中出现两个不稳定系数，分别在第6阶固有频率1 114.4 Hz和第11阶固有频率2 654.3 Hz处，对应的不稳定系数分别为0.004和0.002，这两个结果都小于0.01，可认定为稳定模态。结合后两组仿真结果可以发现，随着均匀磨损量的增加，系统出现不稳定系数的模态数呈增加趋势，而且相比于新制动器，磨损后的制动器不稳定系数在高阶模态中，第三组仿真出现一个近似于0.01的结果，具有一定的发生噪声的倾向。因此，随着磨损量的增加，制动器的系统整体稳定性下降，出现制动低频尖叫声的可能性变大，但是在均匀磨损状态下，磨损量对制动器的系统稳定性影响不大。
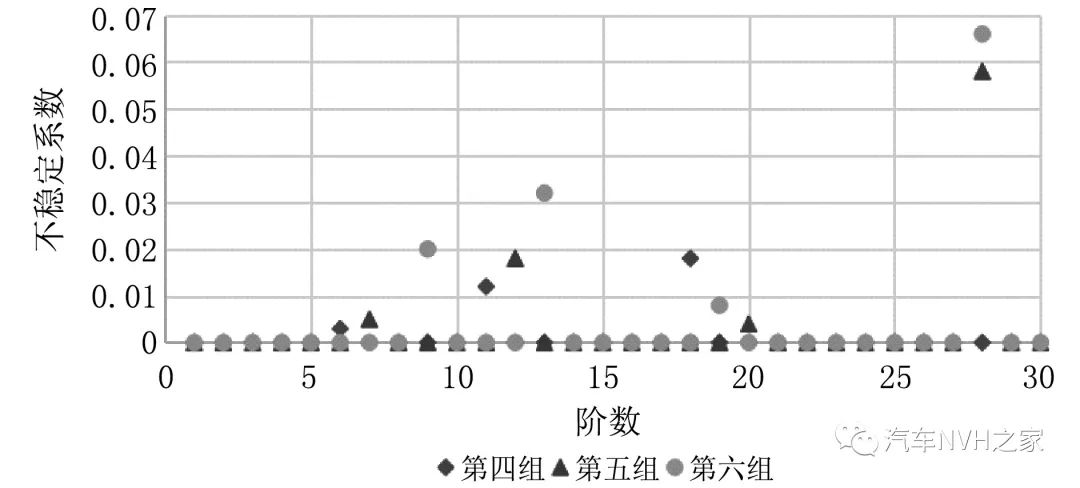
由图9(b)可看出，相对于前3组，不均匀磨损状态下的制动器出现了多个不稳定系数，其中第四组仿真工况(即摩擦片厚度为14 mm且存在1.5 mm偏磨的制动器)出现了3个存在不稳定系数的模态，第16阶模态的不稳定系数为0.003，视为稳定模态，第11阶、第18阶模态的不稳定系数均大于0.01，此时制动器在2 651.2 Hz 和4 065.7 Hz处存在两阶不稳定模态。第5组和第6组仿真各出现4个不稳定系数，其中第5组存在2 760.7 Hz和5 381.3 Hz两阶不稳定模态，而第6组则存在1 846.7 Hz、2 991.5 Hz和5 563.1 Hz三阶不稳定模态。因此，随着磨损量的增大，存在偏磨不均匀磨损状态的制动器发生制动尖叫的机率大幅提升，不均匀磨损对制动器系统的稳定性影响较大。
4.3 仿真结果分析与制动器的优化改进
通过对6组工况仿真结果的综合分析得出，制动器磨损量的大小对其系统固有频率有一定的影响。理想状态下，随着磨损量的加大，固有频率呈降低趋势，这是由于摩擦片厚度变薄后，其刚度下降，从而导致自身固有频率变低。当不均匀磨损发生后，其不稳定模态显著增多，系统稳定性下降，出现噪声的机率明显提升，与现实工况下制动器制动噪声的产生次数随着其使用时间的增加而增多的现象相吻合。
针对因温升而导致的不均匀磨损状态的制动噪声问题，可通过改变其比热容、热膨胀系数、热传导系数等性能参数来解决。采用合适的摩擦材料，通过加入适量特殊元素、调质等处理方法，增大其比热容、热传导系数，降低热膨胀系数，使其在保证制动效果的情况下，降低制动器的整体温升，并改善制动器不同部位的温差，从而改善其温度与应力不均衡的磨损特性，有效地抑制制动噪声。
5 结论
通过对制动器在两种不同磨损状态下的热-结构耦合分析，综合对比6组工况下的仿真结果，得到如下结论：
(1) 摩擦片的磨损对制动器的系统稳定性具有一定的影响，尤其是在实际工况下经常出现的不均匀磨损对其稳定性具有较大的影响。
(2) 在理想状态下，均匀磨损的制动器随着摩擦片磨损量的增加，各阶固有频率基本保持不变，虽然制动器整体稳定性有所下降，但影响不大，这时出现制动低频尖叫的可能性变大。
(3) 不均匀磨损状态下的制动器随着摩擦片磨损量的增加，出现了较多的不稳定模态，系统固有频率出现一定程度的波动，系统的稳定性显著下降，出现制动噪声的几率更大。
(4) 通过对制动器材料的特殊处理，可有效地改善其磨损特性，降低制动噪声。
作者：张雪松1,2， 王兆恒1；1.中原工学院 机电学院，2.郑州经贸学院 机械工程系
广告 
广告
最新资讯
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
-
车载无线广播收音机还需要吗？
2024-12-23 07:37
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
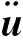
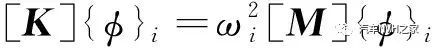
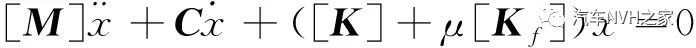
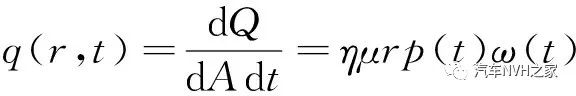
广告
广告
