广告
线控转向系统的自适应神经网络滑模控制
2021-11-04 10:30:46· 来源：焉知智能底盘
作者 | 罗玉涛 郭海文 （华南理工大学 机械与汽车工程学院, 广东 广州 ５１０6４０)汽车线控转向（SBW) 系统取消了传统的转向盘到转向执行机构之间的机械连接,
作者 | 罗玉涛 郭海文 （华南理工大学 机械与汽车工程学院, 广东 广州 ５１０6４０)
汽车线控转向（SBW) 系统取消了传统的转向盘到转向执行机构之间的机械连接, 由电控系统直接进行转向控制, 不仅有利于提高汽车的操纵稳定性和主动安全性, 而且有利于推动汽车电动化和智能化的发展, 是汽车转向技术的主要发展趋势 。针对车轮转角控制的问题, 目前已有多种控制方法应用于SBW系统, 例如PＩD反馈控制和线性二次状态反馈控制 。但考虑系统不确定性和电机力矩扰动时, 上述方法难以满足系统要求的鲁棒性。
传统滑模控制（SＭC) 具有一定的抵抗外部干扰的能力 , 但在设计传统滑模控制器时, 需要预先设定系统干扰的上界值, 而且会存在明显的抖振现象。此外, 有研究表明, 可以通过结合智能控制和滑模控制理论来设计具有良好鲁棒性和稳定性的自适应车轮转角控制器。
基于传统滑模设计了具有在线训练自适应学习算法的二阶滑模控制器, 能够实时估计系统干扰;提出了结合滑模控制和模型预测控制的容错滑模预测控制策略, 使线控转向系统具有更好的鲁棒性和容错能力; 提出了一种自适应的终端滑模控制策略, 该控制策略与传统滑模相比, 不仅能保证系统的有限时间误差收敛性, 而且对系统不确定性和力矩干扰具有更好的鲁棒性; 提出了一种自适应模糊滑模控制策略, 利用模糊理论实时估计滑模控制器的切换增益, 降低了传统滑模控制的保守性, 并减少了车轮转角的抖振现象。
本文针对一种直驱式的线控转向系统构型, 提出了基于径向基（RBF )神经网络滑模控制（RBFSＭC)的车轮转角控制方法; 通过建立SBW系统的数学模型, 分析了系统的不确定性和电机的力矩扰动, 并设计了SＭC和RBFSＭC控制器, 再通过Ｍatlab/ Simuｌink 和CarSim 的联合仿真平台来验证 RBFSＭC的控制性能。
线控转向系统的构型
一种集成了轮毂电机、悬架和转向机构的SBW 系统构型如图１所示。其实现功能的基本原理如下：转向电机输出的力矩经过减速器传递到上转向臂的主销, 上转向臂和下转向臂通过套筒连接, 将放大后的转向力矩传递给车轮轴, 实现车轮绕主销的转动; 当转向结束时, 车轮的回正力矩沿转向时的路径传递到主销, 实现车轮的回正。地面的扰动力矩则经车轮、车轮轴、下连接杆和上连接杆传递到上转向臂的主销, 实现路面的反馈; 减振阻尼、减振弹簧和支撑弹簧起到垂直方向减振缓冲的作用,上、下连接杆起到振动限位的作用, 车轮转角由传感器实时测量, 以实现车轮转角的闭环跟踪控制。
SBW系统的主要参数如下：电机额定力矩Te为1.27Ｎ·m, 电机峰值力矩Tmax为3.8Ｎ·m,电机额定功率Pe为400W, 电机力矩系数kt为0.128Ｎ·m/Ａ, 减速器减速比k为50, 主销内倾角σ为7°, 主销后倾角为２°, 电机转子转动惯量jsm为3.42*10-4kg·m,车轮转动惯量Jｗ为2.1kg·m, 电机转子粘滞系数Bsm为0.004Ｎ·m·s/rad, 车轮粘滞系数Bｗ为9Ｎ·m·s/rad。
线控转向系统的数学建模
转向电机的动力学方程可以表示为
车轮转角控制器设计
3.1 传统滑模控制器设计
由式（5）可知, 线控转向系统的动力学方程可以表示为·δ·ｗ=gu+f（δｗ，·δ ｗ )+d（t)=
式中, Δ为边界层。sat（s)的作用是：在定义的边界层内, 通过反馈控制来减小切换增益较大时滑模切换产生的抖振现象; 在边界外, 采用切换控制, 以保证系统状态快速地趋近于滑模面。
3.2 径向基神经网络滑模控制器设计
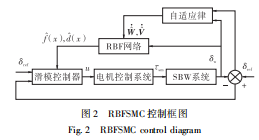
实际上, 车辆行驶时由路面变化引起的系统不确定性具有较大的波动范围, 滑模切换增益取为常数不能有效地削弱干扰的影响, 从而产生较大的转角跟踪误差, 故本文采用RBF神经网络自适应地估计系统的f（δｗ，δｗ )和d（t), 再结合滑模控制方法设计转角控制器, 以实现车轮转角的自适应控制, 其控制框图如图 ２ 所示。
联合仿真试验与结果
本文基于Matlab/ Simulink和CarSim 平台进行联合仿真, 其中选用CarSim中自带的微型轿车模型, 通过屏蔽原有的机械转向系统来实现联合, 整车模型参数如下：整车质量为800kg, 前轴距Lf为1.05m, 轴距L为1.6m, 机械拖距lc为0.018m, 气胎拖距lｐ为0.021m, 车速vCG为18km /ｈ。在车辆维持转向、连续转向和单/ 双移线工况下, 对SＭC和RBFSＭC控制器的动态响应和稳态跟踪性能进行仿真分析。采用图 ３ 所示的车辆前后轮侧偏刚度（CF、Cr)和地面摩擦力矩系数（Fs）来模拟车辆行驶 时系统不确定性引起的干扰; 基于永磁同步电机建立磁场定向矢量控制的电机控制系统模型, 以模拟电机输出的力矩扰动。
图５是维持转向工况下基于SＭC的左前轮转角的仿真结果。图５（a） 说明了车轮转角的快速响应和稳定维持的性能, 在0.3s 时车轮转角能达到期望值, 且存在-0.10°~0.25°的转角误差范围, 当系统总干扰发生变化时, 仍能够保持车轮转角维持的相对稳定。图5（b）表示由路面参数变化引起的系统不确定性和电机力矩扰动组成的系统总干扰, 验证了通过定义车轮侧偏刚度和摩擦系数, 以及建立电机控制系统模型来模拟系统总干扰的可行性。图５（c）表明, 转向电机的控制力矩存在明显的抖振波动, 不利于电机的实际控制。图5（d）表明, 控制器的滑模函数可以维持在０位置附近, 但波动范围较大。
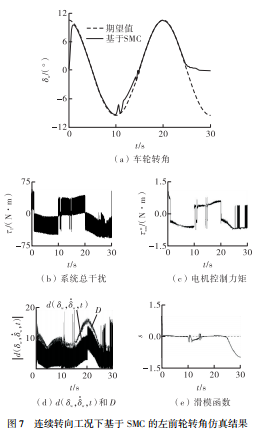
图７为连续转向工况下基于 SＭC 的左前轮转 角仿真结果。图７（a）说明了车轮转角跟踪控制的性能, 在第1.2秒时, 车轮转角达到期望值, 但第10~20秒和第20~30秒时系统干扰发生变化, 车轮转角出现较大的波动, 前者转角波动范围为-2°~0°, 后者转角明显偏离期望的车轮转角, 呈发散趋势。图7（b） 表明, 在３个时间段内呈现出不同幅值变化的系统总干扰, 符合前述参数定义的目的, 验证了通过定义车轮侧偏刚度和摩擦系数, 以及建立电机控制系统模型来模拟系统总干扰的可行性。
图7（c）表明, 在第10秒和第20秒时, 系统参数变化导致 SＭC 的转向电机控制力矩在第10~15秒和第25~30秒时产生明显的抖振现象。控制力矩的抖振会引起转向电机产生较大的力矩扰动, 使得图７（d）中某些时刻系统总干扰上界的实际值d（ δｗ ,·δ ｗ ,t)大于控制器预先给定的上界值D, 导致SＭC不满足Ｌyａｐunov稳定性条件, 从而出现图7（a）中车轮转角波动较大和控制器稳定性变差的现象。图7(e) 表明, SＭC的滑模函数s在第10~15秒和第25~30秒时出现波动和发散的趋势, 存在不满足Ｌyａｐunov 稳定要求的时间点。
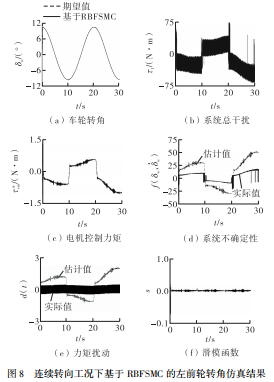
图８为连续转向工况下基于 RBFSＭC 的左前 轮转角仿真结果。图８(a）表明：在第0.3秒时 车轮转角达到期望值, 而SＭCS控制的响应时间为1.2s, 优化了约75% ; 在10秒和第20秒时, 系统总干扰变化引起了转角波动, 其波动范围为-0.23°~0.20°, 经过1s后恢复稳定, 而SＭC的转角波动范围为-2°~0°, 且存在转角控制发散的趋势, 优化了约78% , 故在车轮转角的跟踪方面RBFSＭC更具优势。
图８(c)表明, RBFSＭC较SＭC能够更好地削弱电机控制力矩的抖振现象, 间接地减小了转向电机实际输出力矩的扰动, 使电机输出力矩的控制更加平顺。图８(d)和图８(e) 表明, RBF神经网络基于系统状态x可对系统不确定性 f（δｗ ,·δｗ)和电机力矩扰动d(t)进行实时估计, 能够有效地估计实际值的变化趋势和相对大小关系。图８(f) 表明, RBFSＭC的滑模函数在0.7s 左右时到达滑模面且稳定于滑模面, 进一步验证了RBFSＭC的快速性和稳定性。
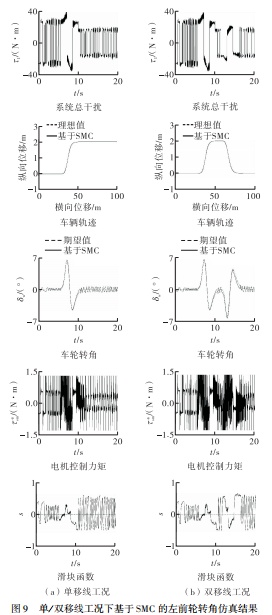
工况３为了进一步验证线控转向系统路径跟踪的性能, 在CarSim中分别建立单移线和双移线工况, 计算出理想路径跟踪时的车轮转角, 并作为对SＭC和RBFSＭC仿真时输入的期望转角。图9为单移线/ 双移线工况下基于SＭC的左前 轮转角仿真结果。
从图中可知：在单/ 双移线工况 下, SＭC可以实现良好的轨迹跟踪, 但SＭC在跟踪期望转角时具有一定的误差, 包括维持０°转角 时-1° ~1°范围的抖振和跟踪动态转角的误差; 转向电机控制力矩存在较强的抖振现象, 不利于电机的实际控制, 其原因是当系统总干扰发生变化且切换项增益η取值较大时会引起明显的抖振; SＭC的滑模函数虽然维持在滑模面的一定范围内, 但明显的抖振现象说明SＭC的稳定性较差, 这说明开发更具自适应性和稳定性车轮转角控制器的必要性。
图10为单/ 双移线工况下基于RBFSＭC的左前轮转角仿真结果。比较图9、10可知：在单/双 移线工况下, RBFSＭC和SＭC跟踪路径的性能差别不大, 但RBFSＭC的优势在于可以更稳定地维持０°车轮转角的跟踪, 且在第10秒时车轮参数变化引起的转角波动更小; RBFSＭC较SＭC削弱了转向电机控制力矩的抖振现象, 更符合电机控制的实际应用; RBFSＭC的滑模函数基本上维持在滑模面附近且较SＭC具有更小的波动范围和抖振现象, 进一步说明了RBFSＭC良好的稳定性和鲁棒性。
结论
本文基于一种直驱式的线控转向系统构型, 提出了考虑系统干扰的自适应车轮转角控制方法。该方法先基于径向基神经网络对系统不确定性和转向电机力矩扰动进行实时估计, 再结合滑模控制理论设计满足李雅普诺夫稳定性要求的车轮转角控制器。理论分析表明, RBFSＭC提高线控转向系统性能的原因在于, 采用了具有强非线性的神经网络对系统中存在的不确定性和干扰进行实时估计, 从而保证转角控制器始终满足李雅普诺夫的稳定性要求, 故较控制器参数固定的SＭC具有更好的转角控制性能和稳定性。
Mat lab/ Simu link和CarSim的联合仿真结果表明：在车辆维持转向和连续转向工况下, RBFSＭC具有比SＭC更好的转角响应和跟踪性能, 具有良好的自适应性; 在单移线/ 双移线工况下, RBFSＭC不仅能够维持０°车轮转角, 而 且能够快速稳定地跟踪动态的车轮转角。因此, RBFSＭC比SＭC能更有效地削弱干扰对系统产生的影响, 具有更好的鲁棒性和稳定性。
- 下一篇：4D毫米波雷达真的来了吗？
- 上一篇：汽车制动助力系统研究进展综述
广告
最新资讯
-
（营运）GBT 22309-2023 制动衬片剪切强度
2024-05-12 09:27
-
中国汽研破局补能焦虑，提供充电桩产品高质
2024-05-12 09:21
-
是德科技手持分析仪新增脉冲发生器选件
2024-05-11 17:38
-
整车下线检测--- 四轮定位
2024-05-11 17:31
-
通用汽车全球汽车试验场布局
2024-05-11 17:24
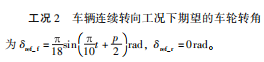
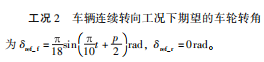
广告
广告
