广告
通过DrivAer汽车模型对比RANS与DES仿真方法
2021-11-13 18:37:02· 来源：AutoAero
摘要CFD是汽车行业十分重要的设计工具。可靠的模拟汽车周围复杂分离流动的分析是节能与降噪来的关键因素。本文比较了RANS模型与RANS-LES混合(DES)模型。使用的是
摘要
CFD是汽车行业十分重要的设计工具。可靠的模拟汽车周围复杂分离流动的分析是节能与降噪来的关键因素。本文比较了RANS模型与RANS-LES混合(DES)模型。使用的是一种公开可实现模型——DrivAer模型。
至今，限于计算资源，相比于很多学术案例，RANS-LES混合法还未在很多复杂几何外形上得到充分研究。本项工作中，对高达3亿个单元的网格分辨率进行了全面评估，并对网格度量进行了讨论。发现对于RANS模型，即使使用高级雷诺应力模型以及高质量网格，也不能捕捉到正确的流场信息。这是因为对初始分离剪切层中的湍流强度预估偏低导致的，这样会使得再循环的预估尺寸偏大。对于阻力系数以及压力分布而言，DES模型效果很好，不同车型之间的趋势于实验值非常一致，但其结果于实验并不是完全一致。最后提出了改进建议并讨论了DrivAer模型与Ahmed模型的相似性。
引入
CFD是当今汽车气动外设计的主要工具。随着计算能力发展，计算软件对于处理汽车中常见的几何外形来说已经足够精细。典型的汽车外形后部会出现一个分离流，对汽车阻力影响较大。但是在车的周围和内部有一些重要的区域，CFD模拟捕捉再循环区域的能力很大程度上取决于湍流模型的预测能力，因此本文对比了RANS和DES两种方法。RANS方法假设湍流的整个谱可以用一组模拟平均流的输运方程来近似，也是基于规范流中观察到的关键物理机制，因此会比那些假设比较少的高阶模型（如LES）以较少的代价来模拟湍流。
混合RANS-LES(本文使用的DES)在分离区维持了LES的准确性，而在边界层由于LES法需要通过各项同性网格来求解整个边界层代价较大，因此在边界层使用RANS法。
到目前位置，汽车行业大部分的湍流模型验证工作由于几何简化（Ahmed或者MIRA模型）受到限制。简化的几何与汽车外形比较类似，但是仍然与实车有很大差距。
虽然在有人全尺寸模型上评估了不同的湍流模型，但由于保密原因，这些内部研究通常不能发表，也因为几何形状和实验数据的限制不能被验证。
DrivAer 模型
DrivAer Model模型是最近提出的公开汽车几何模型，由宝马，奥迪，慕尼黑工业大学汽动与流体力学学院联合研发，有三种形式的外形用于实验研究。在风洞中测量了三种形式的阻力及表面关键部位压力。三种外形分布代表三种典型的汽车形式：直背、快背和阶背。对于每种模型研究了一些变量，包括有无后视镜，有无车轮，详细/光滑地盘。此外每种形式也进行了有、无地面模型两种状态的实验。
之前慕尼黑工业大学的仿真只采用了快背形式并且使用了单一湍流模型。他们的仿真主要精力放在了设置网格以保证收敛和几何变量的研究方面，并没有考虑湍流模型和其他两种形式车身。对于湍流模型，慕尼黑工业大学使用了k-w SST 模型，本文也使用了这种模型。慕尼黑工业大学没有求解近壁面区域，因此很难直接比较，但是一些关键流场区域（例如机舱盖与风窗相交处）的趋势也与之前的研究非常一致。虽然总阻力与实验值非常吻合，但是车身上下部压力分布与实验是有差异的，这就说明一些有些误差相互抵消了。
Ahmed模型
从诸多Ahmed车体的研究种可以得出很多结论。根据后窗倾角不同，存在不同尾部结构（图1）。在0到12°区间，气流很好的附着在后窗，直到离开车体后才发生分离。对于该种形式，大部分RANS模型都有很好的效果，简单模型与高级模型之间也没什么差异。25°形式下，因为气流受到三维分离与后窗及两侧脱落的反向涡对的复杂相互作用的影响，所有的RANS模型都不能正确的模拟出流场。这种情况对于高阶方法例如LES和混合RANS-LES法来说都是个挑战。在25°以后，尤其是35°，气流在后窗和尾部完全分离。RANS模型此时又行了，可以正确预测分离。因此对于Ahmed模型，不同湍流模型的表现与几何外形以及流场情况有关。最近Ashton等人使用同一代码和网格对RANS以及DES进行了比较，发现由于对初始剪切层的湍流剪应力预估偏低，RANS模型都不能够准确捕捉25°时的流场。预估偏低会导致湍流混合程度下降并且循环尺寸过大。如果网格分辨率够高，DES的效果比RANS方法好。如果网格质量差，同等程度的网格，DES比RANS还要差。最后还发现，即使使用最好的网格，由于湍流剪应力比试验值低的比较多，DES法也不能正确的捕捉分离区。在分离点的上游界面处使用单向嵌入式耦合DES法，给DES模型的LES区域提供合适的入流条件，注入合成湍流，这样可以克服上述问题。这可以使剪切层中湍流强度正确，并且几乎完全符合尾流中速度和湍流(以及再循环大小)的实验值。
图1 Ahmed模型
研究目标
本文研究目标包括以下几点：
-
评估DES模型对于汽车周围流场的预测能力以及该方法对于网格分辨率和模型的敏感性。
-
讨论DES模型对于真实汽车模型是否比RANS模型效果好。
-
评估Ahmed模型与DrivAer的相似性。
计算设置
网格与边界条件
研究了两种形式的DrivAer模型：直背与快背（如图2）。在研究不同湍流模型时，保证两种形式网格策略一致。采用光滑底盘使网格差异最小，这样几乎不会改变不同湍流模型的相对误差。计算域及汽车模型示意图如图3。计算域顶部施加滑移壁面条件，高度为8H，入口距离汽车4L，来流速度为40m/s(基于长度L=1.85m,Re=4.87e6),湍流粘度比是20，湍流强度是1%，k,ε,ω值可以由此得到。压力出口距离模型尾部6L，宽度是11W，两侧壁面设置为滑移壁面。地面设置为无滑移且车轮不旋转，与实验一致。这样设置可以减少轮胎旋转导致的模型误差，并且对流场影响很小。
图2 三种形式的DrivAer模型：fastback、estate、notchback
图3 计算域及模型设置
网格
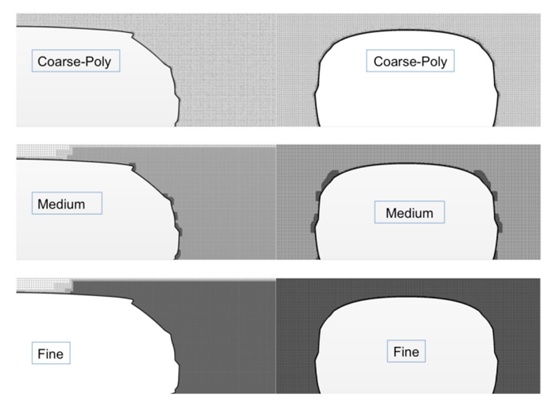
共生成6种网格，其中三个用于DES，详见表1与图4。RANS法的网格设置为多面体、棱柱层；DES法网格为六面体，棱柱层。每种网格在尾部发生分离的部分都进行了多面体/六面体和棱柱层混合细化。每种网格都在边界层进行细化来实现壁面输运方程的插值保证车表面上的无量纲壁面距离y+<1。在整个计算域后部进行了细化（除了近壁面始终是20层边界层），实现网格无关性。早期研究发现RANS模型通过细化多面体网格可以实现收敛。
表1 网格类型及分辨率
图4 用于DES模型的直背式车型网格
对于DES法使用了更多的网格，目的是研究网格敏感性而不是仅仅达到收敛。虽然还可以进一步细化，但目前以足够说明敏感性。本文还专门研究了DES中基于多面体和六面体网格的区别，因为在此类复杂应用中，很少有文献提出最优网格拓扑。
湍流模型方法
本文对几种湍流建模方法进行了评估，单方程模型，可实现k-ε模型，k-ω SST模型，混合涡粘性模型，椭圆混合雷诺应力模型以，SST和SA改进DES模型，延迟DES模型改进延迟DES模型。
混合RANS-LES方法的原理是：传统的壁面解析大涡模拟(LES)对于受近壁面效应影响的高雷诺数复杂流动计算成本太大，通过在边界层中应用RANS模型而在边界层之外使用LES模型，由于RANS模式不需要在边界层中使用精细的各项同性网格，因此可以大大减少网格总数。Frohlich等人对混合RANS-LES方法进行了全面的综述，但在本研究中使用了一种特殊的方法:分离涡模拟。由于这种方法易于实现，并且在许多应用中都表现出了良好的性能，因此它变得越来越受欢迎。
分离涡模拟
分离涡模拟(DES)可以看作是一种RANS模型，它在满足LES网格精细要求的区域使用LES亚网格尺度模型，在网格LES不够精细的区域采用标准RANS模型。
DES最初基于SA模型，其基本原理是基于求解修正湍流粘度的单方程。方程中的长度尺寸为壁面距离d，当取平均假设:产生=耗散时，我们发现:
（1）
其中S是应变率。这是相同的形式的亚网格比例模型，如斯马戈林斯基模型。
（2）
其中
（3）
∂x, ∂y, ∂z是xyz三个方向的网格距离。我们可以用与Δ成比例的长度代替(1)中的d来得到(2)。为了自动选择LES和RANS模式，这种新的长度尺度LDES是基于RANS长度尺度的最小值d和LES长度滤的波宽度， 如下式：
（4）
其中，CDES是一个经验常数，需要以类似斯马戈林斯基常数的方式进行调整，以获得正确的耗散水平。因此，对于具有SA模型的标准DES，网格参数只是决定了模型将在何处采用RANS模型，在何处采用LES亚网格比例模型。
自原始DES方法以来，已有多个改进版本，如延迟分离涡模拟(DDES)和改进延迟分离涡模拟(IDDES)。这些增加了额外的功能，以保护附加的RANS边界层免受LES模式的影响，以允许一些边界层由LES分解，并更快地过渡到可分解的湍流。
本文中，通过商业CFD求解器Star-CCM+来实现这些DES方法的几种改进，特别是使用SST和SA模型的特定版本的DDES和IDDES。
数值方法
在ANSA v14中完成 每个CAD文件的初始预处理，以确保CFD求解器使用合适的初始曲面。然后在商业有限体积代码STAR-CCM+ (v9.0411)中完成了整个模拟，该代码由CD Adapco开发。
RANS
每个RANS计算采用耦合不可压缩非结构化有限体积求解器。采用二阶迎风格式对动量和湍流方程进行离散。采用V循环的代数多重网格(AMG)方法计算动量方程，用弯曲循环方法计算湍流量。使用网格序列初始化(GSI)方法进行初始化,可以在一系列粗网格上求解一个全隐式完全牛顿解算方案算法来计算一阶非粘流解,它给计算域提供了比指定常量值更好的初始流场的速度和压力。在400个案例中，所有的模拟都一直进行到阻力和升力系数的标准偏差低于2E-5。这个准则与动量方程和湍流方程与的残差误差在1E-5以下一起使用。这两个都是用来确保流动达到完全收敛，通常会跟据湍流模型的不同再在2000-5000次迭代之后达到。
DES
所有的DES计算都使用了分离不可压缩非结构化有限体积求解器。采用混合数值格式离散动量方程的对流项，该格式在LES的区域采用有界中心差分格式(CDS)，在RANS区域采用二阶迎风格式。湍流量采用二阶迎风格式。采用代数多重网格(AMG)方法，动量方程采用V循环，湍流量采用弯曲循环。使用稳定的RANS结果初始化。粗、中、细网格的时间步长分别为ΔtU/L=1E-033、5.5E-04、4E-04。每次模拟运行5个对流单元(t=5L/U=0.23s)，然后运行20个对流单元(0.92s)进行时间平均统计。
结果
RANS
测试了5个RANS模型; 可实现的k-ε，k-ω SST,Spalart-Allmaras, B-EVM和EB-RSM。这些阻力系数的计算结果汇总在表2中。实验数据没有提供升力系数，因此本文的分析仅限于阻力系数和压力系数。可以看出，没有一个湍流模型能正确预测所有外形的汽车模型。虽然一种模型可能在一种外形下表现良好(如正面的SST)，但它也无法预测其他车型的正确阻力值。
表2 RANS模型测得的阻力系数
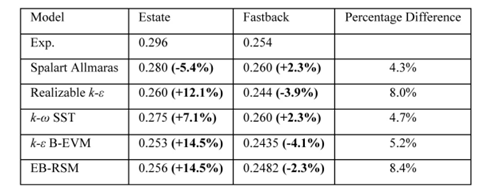
模型之间的大多数差异发生在后部分离区域，因为里是最大的分离区域。表3通过展示直背和快背式之间的阻力系数的差异为我们提供了进一步的了解。虽然所有模型都捕捉到了阻力系数降低的趋势，但它们都未能捕捉到具体数值，其中SA模型最准确，误差为52%(更差的有80.9%的误差)。通常对于工业汽车流来说，RANS模型无法捕获绝对力系数，因此它们被用来评估趋势的大小和方向。没有进一步的实验数据也就不能正确地评估这些模型为何失败,但是可以从艾哈迈德车身吸取一些经验,在25度的情况下，所有模型都对初始分离剪切层中的湍流切应力预估偏低，意味着更少的湍流混合和更长的分离区。未来PIV研究这些DrivAer模型后,将会提供进一步的线索，其中尾流中湍流动能(TKE)强度似乎表明艾哈迈德车身更适用于这种情况。
表3 不同RANS模型对于直背式和快背式的阻力系数差异
无论哪种湍流模型，都不能正确预测流动(网格细化评估高达8000万个单元)，这也是本文测试混合RANS-LES模型的主要动机。虽然不能说没有RANS模型能够正确地预测流场，但目前的模型还没有体现出可接受的效果。DES方法的使用应该可以改进后分离区域的预测，本文将评估这一差异有多大，以及这对模拟设置的敏感性有多大。
混合RANS-LES （ DES）模型
混合RANS-LES方法的一个重要研究方面是网格细化。RANS和LES区域应考虑每种模型的网格分辨率要求，即LES区域的LES分辨率和RANS区域的RANS分辨率。
我们使用了三种网格，首先是由8000万个多面体单元组成的RANS网格，其次是基于六面体“微调”网格的两种进一步细化的网格，选择这个网格是因为它产生的单元具有更结构化的排列，应该会减少梯度计算错误带来的数值耗散。
在细化研究中，每个网格都使用SST-IDDES模型，并对时间步长进行调整，以确保区域内的CFL数小于1。
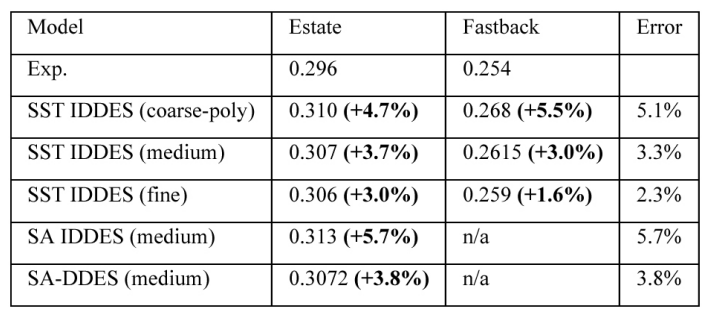
阻力系数计算结果见表4、表5，压力系数计算结果见表5、表6、表7。网格敏感性研究表明，从粗网格到细网格，Cd呈不断减小的趋势，直背形式尤其明显。值得注意的是，虽然细网格只是5个对流单元的时间平均，所以平均值可能随着进一步的时间平均略有变化。最大的变化是从粗多面体网格到中六面体网格，这表明多面体网格有额外的数值耗散(粗网格和中网格之间只有2000万网格的差异)。这些变化也可以从图5、6和7中观察到，在图5、6和7中，后窗Cp有一些变化，但这只是通过对称平面(y=0)的，所以变化不是很明显。
表4 每种DES网格得到的直背与快背平均阻力系数
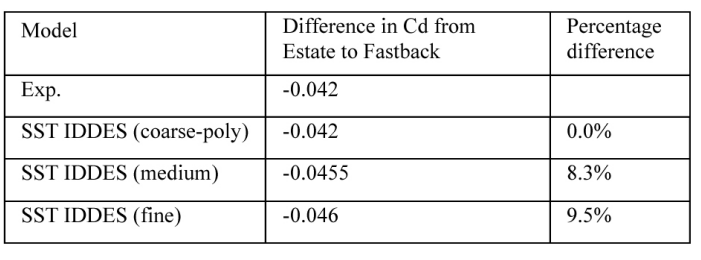
表5 不同DES网格对于直背式和快背式的阻力系数差异
图5 快背式车型使用SST IDDES 模型不同网格的车底平均压力系数
图6 快背式车型使用SST IDDES 模型不同网格的车顶平均压力系数
图7 直背式车型使用SST IDDES 模型不同网格的车顶平均压力系数
表5提供了直背和快背形式之间阻力系数的变化。与表3的RANS结果相比，可以看出，不仅趋势方向正确，而且大小也更接近，所有网格的相对偏差小于10%，而最佳RANS模型的相对偏差为52%。因此，尽管DES模型的阻力系数绝对值仍然不正确，但趋势预测得很好，这使得在工业CFD过程中使用DES比RANS模型更有吸引力。
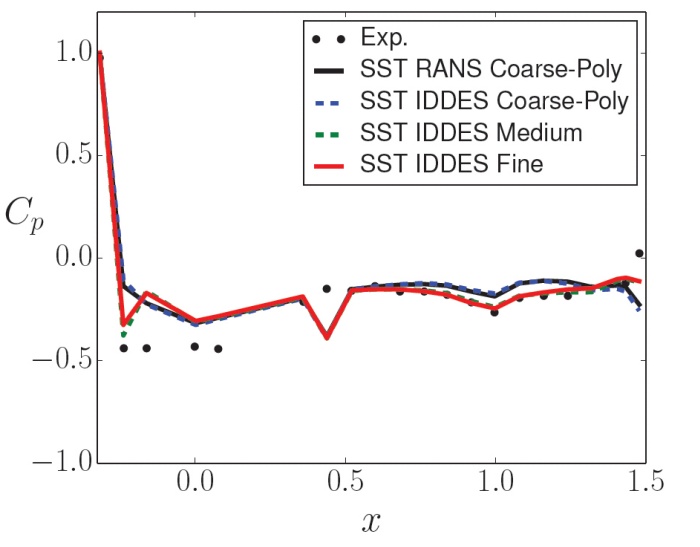
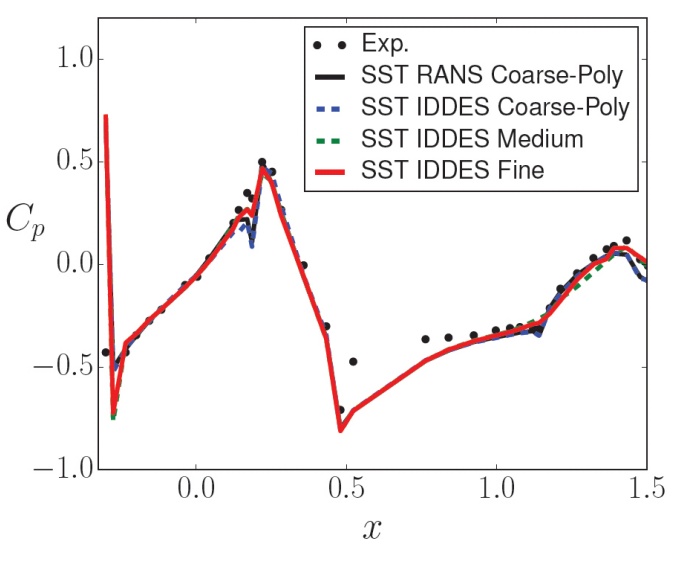
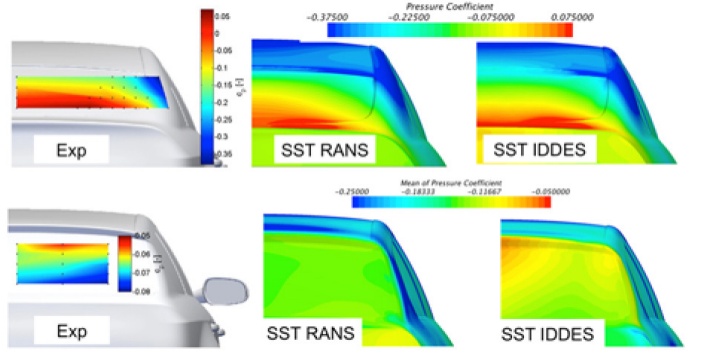
图8和图9更清楚地展示了模型之间的差异。这些图显示了实验数据在直背和快背形式的后窗上的CP分布。对于快背形式，RANS和DES方法预测的分布与实验数据相似，但都低估了压力恢复。对于直背形式，RANS和DES方法都不能捕获正确的分布。然而，由于在CFD模型中无法精确地复现风洞域，可能会有差异，从而影响压力系数。DES和RANS模型都过度预测了尾部负压，表明分离预测过大。在所有改进DES之间也有很小的差异(相对于实验和RANS结果)。不幸的是，没有来自实验的表面摩擦或油流数据，但很明显，直背形式的模拟是最具挑战性的。DES模型比RANS模型具有更好的一致性，这在阻力系数中有所反映。然而，阻力系数是一个全局量，所以它在无法确定模型在何处为何失败。
图8 直背和快背式实验与仿真（SST RANS and SST-IDDES）压力系数分布
图9 直背式实验与仿真（DES）压力系数分布
网格分辨率
我们可以从前面的所有数据中看到，首先，RANS模型都不能正确预测任何形式的阻力或Cp，虽然DES方法可以更好的预测，但它们仍然不能预测正确的流场，特别是对于直背形式而言。然而，最有趣的结论之一是，相对于RANS模型之间的大分布，网格和DES模型类型相对不敏感。图12、13、14、15显示了RANS模型或更准确的有效亚网格尺度模型(建模湍流动能(TKE))和分解流本身(分解湍流动能(TKE))的贡献。不幸的是，没有相应的实验数据，但这些量有助于评估LES模型在何处有效以及模型的相对贡献。
直背式网格敏感性
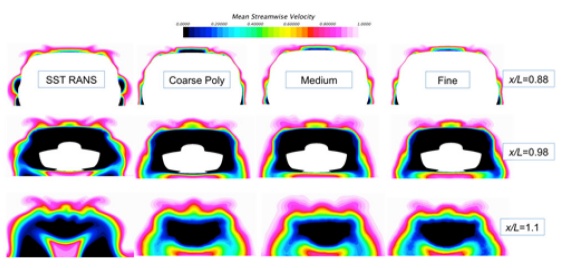
从图10中可以看出，与SST-RANS结果相比，所有DES的结果从尾部分离较少，尾迹模式不同。粗多面体网格和中等六面体网格间的流向速度差异最大。中网和细网之间差别不大(分别为80×106和300×106 单元)。图11和图12为湍动能(TKE)的求解和建模，其中:
（4）
（5）
根据边界层理论，我们可用下式获得模型的雷诺应力：
（6）
对于TKE，我们可用下式得到：
（7）
（8）
图10 用于分析的直背与快背式平面
图11 快背式SST-IDDES 和SST-RANS模型三种网格分辨率平均流速
图12 快背式SST-IDDES模型三种网格分辨率的平均湍动能
从图11和图12中可以看出，首先，与求解内容相比，建模的贡献很小(5%)，这表明模型在这些位置处于LES模式下运行。然而，这并不能告诉我们求解的湍流程度是否足够高。对于Ahmed模型，我们发现所有RANS模型与实验数据相比都低估了初始分离剪切层中的湍流程度，甚至在精细网格下的改进DES也是这样。
在图12中，可以将SST-RANS模型预测的TKE程度与DES求解的TKE进行比较。与Ahmed车身类似，可以看到RANS模型预测的TKE值低于任何改进DES模型。这解释了为什么RANS模型在图11中显示出更大的流动分离，因为降低TKE程度会导致更低的湍流混合水平和更大的再循环区域。
网格分辨率评估
使用DES(以及混合的RANS-LES模型)的一个常见挑战是评估网格分辨率是否足够。对于RANS方法，可以通过网格细化可以达到目的，即网格的进一步细化不会改变流场。对于混合的RANS-LES方法，达到网格收敛是不可能的，因为网格越细化(在LES区域)，滤波的宽度越小，湍流谱的分辨率就越高，直到达到准dns分辨率。虽然精确的网格收敛是不可能的，但应该可以达到一个网格分辨率，其中流量的数量是相对稳定的，以进一步细化网格。
这部分我们关注三个指标，如图14所示：
1. 湍流粘度比
2. 网格大小与Kolmogorov长度尺度
3. 网格大小与积分长度比例。
湍流粘度比νt/ν可以被认为是SGS(模拟湍流)对整体耗散水平贡献的度量。一个单位值将意味着模型中的湍流与分子粘度本身处于同一水平。有效地，它给出了与最小的Kolmogorov尺度相比的过滤器宽度相对位置测量，该尺寸分子粘度本身将最小的结构耗散为热量。
对于壁面分解LES，之前的研究通常旨在达到2-5的比例，但这是相对低雷诺数流动。本研究中最粗的网格在后分离区域的比例超过50(平均约为70)，而最细的网格的比例约为10，这表明网格分辨率很精细。
LES的目的是模拟较小的各向异性尺度，并解决更大的各向异性尺度。滤波宽度(DES的滤波宽度是网格大小本身)假定LES位于能谱的惯性范围内。这是描述最大尺度湍流的能量，包含尺度和定义最小尺度的Kolmogorov尺度之间的范围。在较高的雷诺数下，这个惯性范围覆盖了更大的频谱，因此你可以远离Kolmogorov尺度(更高的湍流粘度比)，但仍然在惯性范围内。
第二个度量是网格大小与Kolmogorov长度尺度的比，被定义为：
其中，ν为分子黏度，Δ为网格大小，ε为来自于RANS结果的湍流耗散率，这里ε为整个模型耗散率。当然，RANS模型中的任何错误都意味着ε的精确值可能是不正确的，但这些度量的目的是比较不同的网格，而不是确定其精确值。这个度量评估了网格分辨率与最小的湍流尺度(Kolmogorov长度尺度)的比较情况。Pope认为这个比例应该约为12，从图14中可以看出，粗网格的比例约为>150，最细网格的比例约为80。这比建议的比率要高得多，但同样，由于雷诺数更高，这只是从最小尺度的测量，所以滤波器宽度仍然可以正确地在惯性范围内。
从湍流尺度的另一方向看最后一个度量是Kolmogorov长度尺度，Kolmogorov长度尺度是定义含能范围的积分长度尺度。被定义为:
这个比例的统一值意味着网格只精细到足以解决包含能量的范围，因此没有进一步精细到足以捕捉较小的尺寸。图14所示的后窗上方最粗糙的网格值小于或等于1的区域的车身后部大约大约为5-7。之前有人研究了积分长度尺度和泰勒微尺度(定义惯性范围)之间的关系，建议理想的网格尺寸应该是积分长度尺度的十分之一，从而正确解析惯性范围，因此Lratio应该大于10。我们的细网格最接近这个值，这表明这是唯一遵循这些指标的网格，因此它与实验数据最接近。未来的工作将是将这种分析扩展到直背形式，并进一步研究得出一个新的度量来评估DES的理想网格分辨率。
图14 DES网格量度
直背形式——改进DES
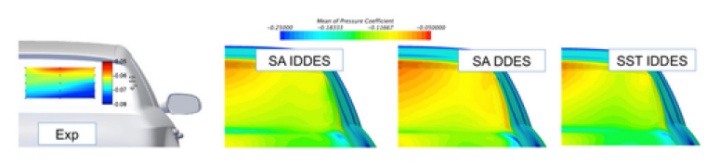
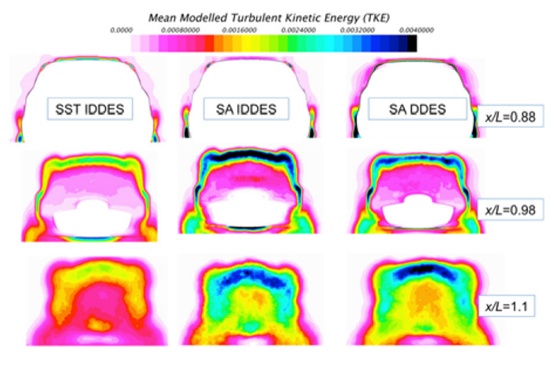
图14、15和16展示了不同改进DES的直背形式的平均流向速度、模型TKE和解析TKE。可以观察到与快背式相似的结论，RANS模型预测了较低水平的TKE，因此出现了比任何DES变体更大的再循环区域。
有趣的是，虽然纯RANS模型中的SA和SST模型在Cd和再循环区域大小上有相当大的差异，但在DES模式中，它们预测的流场形式基本相同。对于这种形式，最具挑战性的区域是后窗分离区，因此在LES中，每个模型都简化为Smagorinsky式的亚网格模式，这就可以理解为什么流动形式基本相同。然而，阻力系数中可能存在一些误差抵消，就掩盖了模型之间的差异。然而，从图14、15和16中可以看出存在相似的TKE程度和流向速度。模型中的TKE值存在一些差异，但由于这一量级仅占TKE总量的5%，这些变化似乎不会在很大程度上影响流向速度。
图15 直背式改进DES和SST RANS方法的平均流向速度
图16 直背式三种改进DES的平均RKE
图17 改进DES和SST-RANS模型的平均RKE
DES模型的整体性能
虽然已经确定改进DES(对于任何六面体网格)比RANS模型精度更好，但阻力系数和后窗Cp仍然至少有3.5%的误差。研究表明相对RANS-DES模型，DrivAer汽车表现的性能的似乎与Ahmed车体的特征类似(TKE和再循环的尺寸),因此,TKE程度和初始分离剪切层可能仍被低估，导致太大的再循环尺寸。这也与图7和图8一致，图7和图8高估了直背式的再循环。Ahmed车体的解决方案是在单向耦合嵌入DES区域注入合成湍流，从而克服了初始分离剪切层中TKE的不足。
总结
进行了基于真实汽车模型：DrivAer的RANS和DES模型的详细研究。各种RANS模型，从1方程Spalart Allmaras模型到全低雷诺数Reynolds Stress模型，都不能正确捕获流动。在三个相继加密的网格上，对两种形式的车型进行了几个改进DES的测试。结果表明，与RANS模型相比，DES模型在力系数和Cp分布以及不同车型的总体趋势方面具有明显的优势。评估了几种网格量度来评估网格分辨率，结果发现只有细网格满足LES区域的标准网格要求。尽管可能存在某种错误消除因素，掩盖了更大的差异，但是在不同的改进DES中，对底层RANS模型的敏感性并不高。
文献来源：
CITATION: Ashton, N. and Revell, A., "Comparison of RANS and DES Methods for the DrivAer Automotive Body," SAE Technical Paper 2015-01-1538, 2015, doi:10.4271/2015-01-1538.
AutoAero是吉林大学张英朝教授团队建立的专业汽车空气动力学微信公众号号，致力于普及汽车空气动力学知识，传播汽车空气动力学。推广包括流体力学基本理论，汽车空气动力学及热管理水管理等基础知识，乘用车气动造型设计，卡车气动造型设计，风洞实验技术等多方面的内容。欢迎有兴趣的专业人士阅读、关注、共享！
- 下一篇：最新！中国电动汽车现行标准
- 上一篇：纯电动汽车电机驱动系统三相线滤波磁环设计
广告
最新资讯
-
直播｜中汽中心 工程院：整车碰撞精准化仿
2024-05-21 18:24
-
R101规定的电动车辆纯电续驶里程的测试方法
2024-05-21 18:14
-
计量夯基 向新而行 | 海克斯康2024“世界计
2024-05-21 17:39
-
涡旋式汽车空调压缩机怠速异响分析与控制
2024-05-21 17:19
-
新能源汽车整车热管理标定方案
2024-05-21 15:59
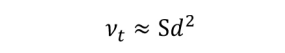
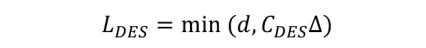
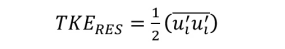
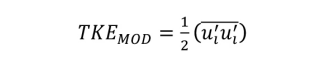
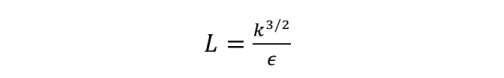
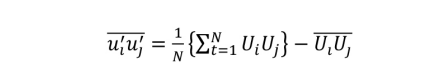
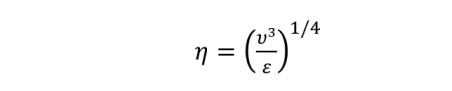
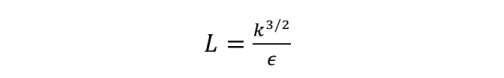
广告
广告
