寻找供应商
广告
首页 > 汽车技术 > 正文

东风汽车 | 带温度因子的锥离子电池模型研究

2021-11-13 22:52:49·  来源：电动学堂  作者：罗冬等  
　
文章来源:东风汽车集团有限公司岚图汽车科技分公司引言车用动力捚离子电池系统是电动汽车上最常见的储能装置｡准确的电池模型对于提高电池的能量利用率､延长电
文章来源:东风汽车集团有限公司岚图汽车科技分公司

引言

车用动力捚离子电池系统是电动汽车上最常见的储能装置｡准确的电池模型对于提高电池的能量利用率､延长电池系统使用寿命极为重要｡目前,电池模型包括:电化学模型､经验公式模型以及等效电路模型等｡

电化学模型是由一组描述电池内部电化学反应机理的偏微分方程构成｡从理论是上讲,电化学模型可以准确地表征电池外特性以及电池内部电化学反应过程,但是由于偏微分方程求解过程复杂､计算量大,在嵌入式系统中推广使用有一定的难度｡为了降低计算量,很多学者提出了多种简化偏微分方程组的方法,其中包括:Pade近似法､抛物线近似法等｡

经验公式模型与等效电路模型类似,不需要深入了解电池内部化学反应机理｡它通过一定的数学关系式来拟合电池外特性变化｡经验公式模型包括:Peuk方程､Shepherd模型､Unnewehr模型､Nemst模型等｡等效电路模型是通过电阻､电容､电压源等电子元器件来描述电池的非线性特性,包括:RC回路模型､四阶动态模型､PNGV模型等｡这两种模型结构简单,需要标定的参数少且容易执行,因此,在电池管理系统开发过程中得到了广泛应用｡

不管采用哪一种电池模型,其待定参数均与温度密切相关｡由于电动汽车的运行温度区间较大,为了让电池模型精确地模拟电动汽车使用过程中的电池外特性,在实际使用过程中电池模型参数通常通过查参数与SOC和温度对应关系的二维表获得｡

本文通过研究一阶RC等效电路模型中参数与温度的依存关系,建立电池模型中参数的温度因子模型,提出了一种带温度因子的电池等效电路模型,并对带温度因子的电池等效电路模型精度做了验证分析｡

1 一阶RC等效电路模型
电池RC等效电路模型可以通过增加电路中RC网络(电阻与电容所并联组成的回路)的数量来增加模型精度,然而,过多的RC网络会使计算量增加｡图1为一阶RC电池等效电路模型原理图,电压源描述电池的稳态开路电压,电路的其他部分描述电池的欧姆内阻特性和弛豫效应｡U,,为电池开路电压,U表示电池工作过程中的输出电压,R,为电池内部欧姆内阻,Ri为电池极化内阻,T为电池极化时间常数｡
假设在t→(t+Llt)时间内,电流I(t)为恒定值,则式
(1.2)可表示为:
2—阶RC等效电路模型参数辨识
 
本文以镍钴锰酸锂(NCM)电池为研究对象,在不同温度下,采用NEWARE电池单体充放电设备和恒温箱开展实验｡根据文献中提到的电压脉冲响应试验(VoltagePulseR吓ponseTest,VPRT)设计试验方案｡考虑到在纯电动汽车(ElectricalVehicle,EV)上电池系统通常采用几个单体电池并联的方式,在使用过程中单体电池的充放电电流小于lC｡为了让电池模型更准确地模拟纯电动汽车行驶过程中电池的外特性,本文对原有的VPRT试验方案进行了改进,改进后的方案如下:首先以lC倍率放电10s,接着静置40s,然后以lC充电10s,最后静置40s｡

实验步骤:工在25°C下将电池调整至满电状态;心在25°C下,采用l/3C放出5%的电池容量;在测试温度下充分静置以平衡电池内部与外部的温差;j进行一次VPRT循环,记录电池的电压､电流以及容最变化值;重复第2到第@步,以此类推,可分别获取SOC为95%､90%､85%､80%､75%一直到5%时的VPRT测试数据｡

根据VPRT实验数据离线辨识电池模型参数的流程步骤如下:
(1)确定电池的开路电压U｡将同一VPRT循环过程中的静置过程端电压均值作为该SOC点对应的开路电压｡
(2)根据由放电至静置和由充电至静置这两段电压跳变计算出放电和充电欧姆内阻,然后将二者平均确定电池的欧姆内阻Rohrn
(3)根据uoc､R0hrn以及U1可以获得电池的极化电压,然后通过离线优化得出极化内阻Ri和极化时间常数T｡

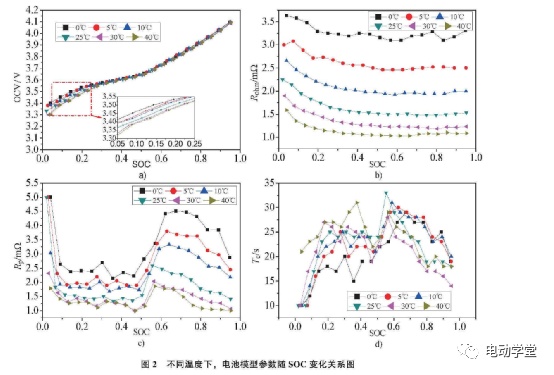
通过上述方法优化得到不同温度下电池模型的参数,如图2所示,其中图2a为ocv曲线随温度变化对比图｡从图中可以看出,在SOC大于30%的区间内,温度对OCV的影响很小,在0~30%SOC区间内,温度越高,OCV值也相应越高,但是在同一SOC点,OCV值受温度影响较小｡图2h､(､d分别为不同温度下放电时的欧姆内阻､极化内阻以及极化时间常数随SOC变化的曲线图｡从图中可以看出,随着温度升高,欧姆内阻值和极化内阻值会相应地减小,而极化时间常数值与温度高低关联性不大,大部分情况均在20~30s间波动｡

3带温度因子的电池模型建立及参数辨识

为了在电池管理系统控制算法开发过程中尽可能简沽地使用电池模型参数,本文将不同温度下的极化时间常数设为定值23s(所有极化时间常数的均值),再采用上述方法,

重新离线辨识RP,得到不同温度下的Rp值｡这种做法对电池模型精度的影响将会在文章后续章节分析｡

为了研究欧姆内阻和极化内阻随温度的变化关系,本文采用式(3.1)计算任意温度下的欧姆内阻与25°C下的欧姆内阻的比值,采用式(3.2)计算任意温度下的极化内阻与25°C下的极化内阻的比值｡

式中,T11为欧姆内阻的温度因子;兀为极化内阻的温度因子;rT为x"C对应的开氏温度值,单位为K;R,,w,(T,,SOC)表示由温度和SOC对应的欧姆内阻值｡式中类似的表达式也是相同的含义｡
人们普遍认为,温度对化学反应速率的影响遵循An如-niu寸定律[10]｡由于电池模型参数中的欧姆内阻和极化内阻从本质上讲也受到电池内部化学反应速率的影响,因此,本文假设T11和T,2的取值与温度的关系符合式(3.3)｡

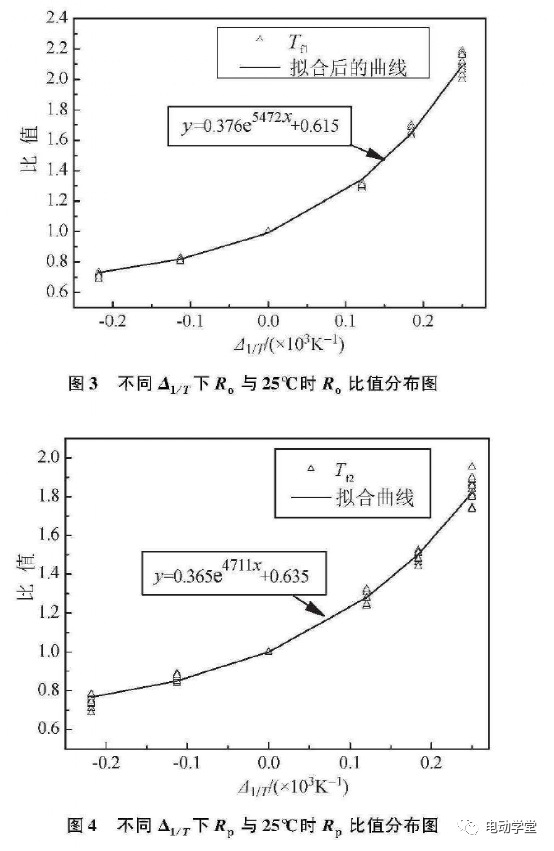
图3为任意温度下的欧姆内阻与25°C下欧姆内阻的比值以及其拟合曲线｡图4为任意温度下的极化内阻与25°C下极化内阻的比值以及其拟合仙线｡

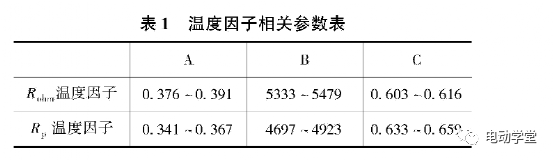
为了确定对任意温度都适用的R,h,,和Rl的温度因子函数,本文采用式(4.3)拟合根据实验以及数据处理获得的T11和T,2离散点,分别得到了确定温度因子函数需要的A､B､C的取值范围,见表l

4实验与仿真结果分析
从图2可以看出,电池内部温度越是偏离25°C,其电池模型的参数差异也越大,所以本文选取0°C､25°C和40°C,分两步验证所提出的电池建模方法的精度｡电池模型验证分析分为两步:一是在0°C､25°C和40°C时,仿真分析将极化时间常数定为23s对电池模型精度的影响;二是在40°C和0°C时,对比分析带温度因子的电池模型与传统电池模型的精度｡为了评价不同电池模型的精度,在电池模型仿真的每个时刻均求一次仿真误差的均方根,称为动态均方根误差(DynamicRootMeanSquareEn､or,DRMSE),并将NEDC工况对应的电池输出功率谱导入充放电设备开展单体电池工况测试试验｡试验过程:将单体电池恒流恒压充满,然后调整至90%soc点,按照NEDC工况的电流谱循环放电20次终止试验｡

4.1极化时间常数简化前后的电池模型参数精度验证
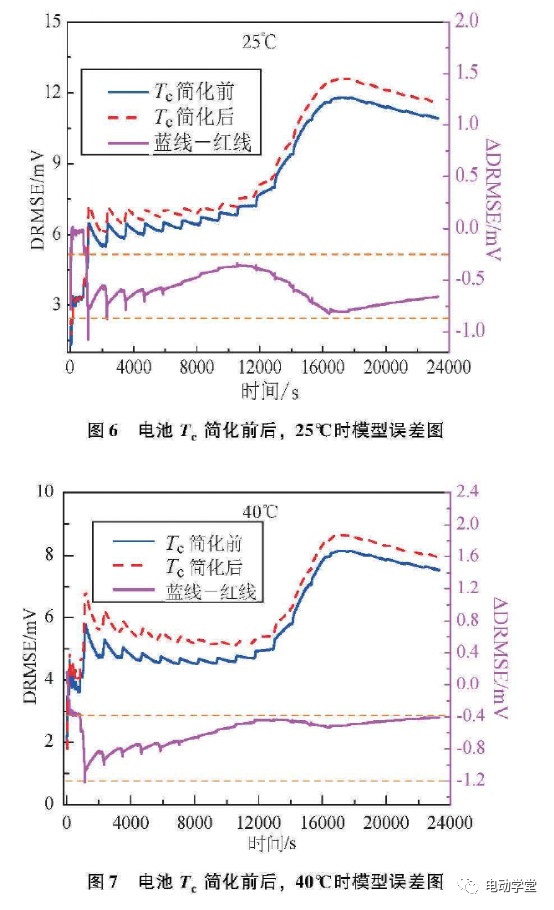
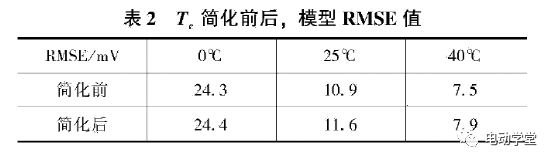
图5~图7分别为0°C､25°C以及40°C时,时间常数简化前后模型参数的DRMSE曲线｡从图中可以看出,DRMSE曲线前半段与后半段相比,波动更剧烈,这是由于前期获取到的误差点个数少,DRMSE值更容易受某一点的误差影响;在DRMSE曲线的后半段有下降的趋势,这说明后半段与中间段相比,电池模型的精度更高｡表2为不同温度下,时间常数简化前后电池模型的误差均方根值｡从表中可以看出,在不同温度下简化前后电池模型精度变化不大,DRMSE值简化前后最大的变化量小于lmV｡



4.2带温度因子的电池模型精度验证
本文将采用温度因子计算得到电池模型参数的方法称为带温度因子的电池模型,将采用辨识得到的电池模型参数的方法称为传统模型｡
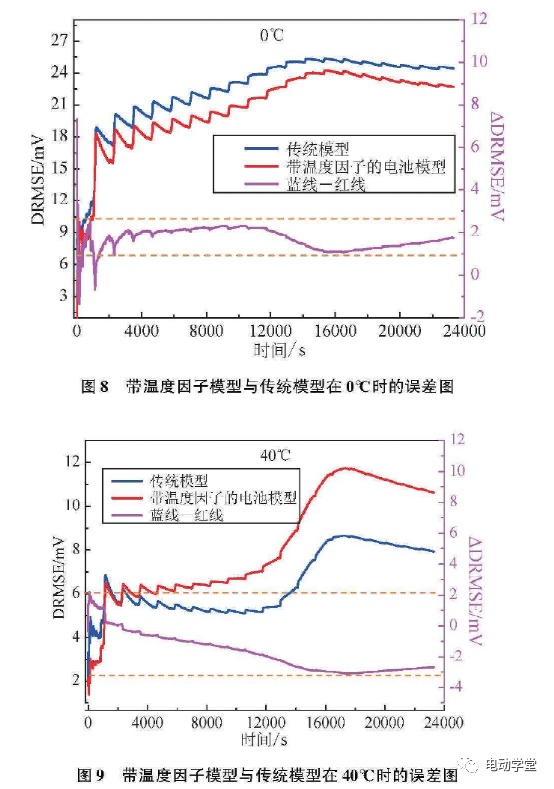
图8和图9所示分别为0°C和40°C时,采用温度因子简化前后,电池模型在NEDC工况下的仿真DRMS变化曲线｡从图8可以看出,0°C时,简化后电池模型的精度与简化前相比有所提高,这从侧面证明了采用温度因子简化电池模型参数的合理性｡从图9可以看出,40°C时,简化后电池模型精度有所下降,DRMSE值最大不超过3mV,由于40°C时简化前电池模型的精度很高(DRMSE值最大约为8111V),简化后电池模型的DRMSE值最大约为12mV｡

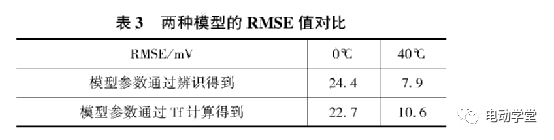
表3为整个仿真过程中传统模型与带温度因子的电池模型的仿真误差的均方根值｡从表中可以看出,0°C时,带温度因子的模型比传统模型的RMSE值要小,而在40°C时,带温度因子的模型比传统模型的RMSE值要大,但是总的来说,带温度的电池模型的误差也不是太大｡

综上所述,带温度因子的等效电路模型对NEDC工况的仿真误差RMS值小于25mV｡对于三元电池来说,SOC每变化5%,电池的开路电压就会变化约50mV,也就是说,因为带温度因子的电池模型导致的SOC估算误差小于5%,所以,带温度因子的电池模型精度能够满足工程实践对电池模型的需求｡

5结论
本章首先通过不同温度点VPRT实验测试数据辨识出了不同温度下的电池模型参数,然后再将不同温度､不同SOC点下的极化时间常数设为定值再重新辨识不同温度点下的极化内阻,最后采用温度因子对不同温度点的电池模型参数做了简化｡在MATLAB/Simulink中建立电池模型,根据不同温度下的NEDC工况测试数据,对带温度因子的电池模型展开仿真分析,得出结论如下:

(1)带温度因子模型与传统电池模型相比,在嵌入式系统中占用的计算资源更少｡
(2)在不同温度､不同SOC点下,电池模型的极化时间常数可设为定值｡极化时间常数简化前后,电池模型的均方根误差值增加量小于lmV｡
(3)带温度因子的电池模型精度较高,对SOC估算造成的误差较小｡在0°C时,带温度因子的电池模型的精度与传统模型的仿真误差的RMS值分别为24.4mV和22.7mV,带温度因子电池模型的精度更高;在40°C时,带温度因子电池模型的精度与传统模型的仿真误差的RMS值分别为10.6111V和7.9mV,虽然带温度因子电池模型的精度稍差,但是其精度依然较高(仅为10.6111V),对SOC估算造成的误差较小,可以满足工程实践对电池模型精度的要求｡
分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 区域化配电的技术及趋势 • 汽车制动踏板感匹配方法探讨
• 电动汽车动力电池碰撞安全性及建模仿真 • 欧盟2023年温室气体排放下降8.3%，交通运输脱碳需奋起直追
• 详解！续航2900公里的康明斯燃料电池卡车-H2Rescue • 电动汽车轮胎的特点和创新要突出的技术亮点
• 大众PEP开发流程详解 • 一文讲清全球定位系统GPS
• 中国汽研携手东盟MIROS成立“商用车测评国际联合研究中心 • 重型商用车油耗新标准颁布
0 条相关评论
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25