广告
优化思想及KKT原理在换道决策中的应用
2021-11-23 10:43:13· 来源：智能运载装备研究所
在车辆的实际避障过程中，决策规划是自动驾驶最重要的部分之一。决策规划系统在融合多传感器信息之后，在基于车辆动力学的同时结合驾驶需求进行车辆行为的实时决
在车辆的实际避障过程中，决策规划是自动驾驶最重要的部分之一。决策规划系统在融合多传感器信息之后，在基于车辆动力学的同时结合驾驶需求进行车辆行为的实时决策规划，主要分为行为决策和运动规划两部分，行为决策在满足交通规则、行驶安全性等约束条件的前提下求解最优的驾驶行为意图；而运动规划主要是根据车辆运动状态和已知的环境信息，在考虑多重复杂约束条件下，实时规划车辆的期望运动轨迹，以保证车辆的安全性和舒适性。本文主要以换道决策为例，对其中的优化问题展开描述，以求加深对优化建模与KKT原理的理解。
图1 决策规划-分层体系结构图
采用横纵向非解耦五次多项式方程来描述换道路径：
其中，
即
其中，x代表纵向位移，y代表横向位移，ai表示多项式拟合系数，以开始换道避障时刻建立相对坐标系如下图所示：
图2 换道避障过程示意图
图中(x0,y0)即为原点(0,0)，xend和yend分别表示换道完成时刻的纵横向位移，其中在行为决策过程中，假设横纵向位移未知，本文将设计关于行为决策层和运动控制的紧急转向避障系统。
假设换道过程的边界约束条件为：
其中，K表示曲率即
则边界约束为
求解可得多项式系数为
则换道路径为
考虑在紧急避障过程中，轮胎极有可能会出现高饱和并开始侧滑的现象，因此需要在紧急转向避障过程中保证车辆的稳定性。因此，在行为决策时必须考虑车辆动力学约束条件，设计一个动态风险评估模型，用来持续评估碰撞与车辆稳定性的相关风险。
车辆质心处的横向加速度为：
其中，
其中，vx为纵向速度，vy为横向速度，γ为车身横摆角速度，β为车身侧偏角。则车辆横向加速度为
横向加速度受轮胎与路面之间附着系数的约束，它们之间的关系为：
其中，
其中，μ是路面与轮胎之间的附着系数，g是重力加速度。假设
其中，k是一个动态系数。则
根据车辆运动学，车辆横摆角速度为
结合换道路径的五次多项式方程，可得横摆角速度为
其中，
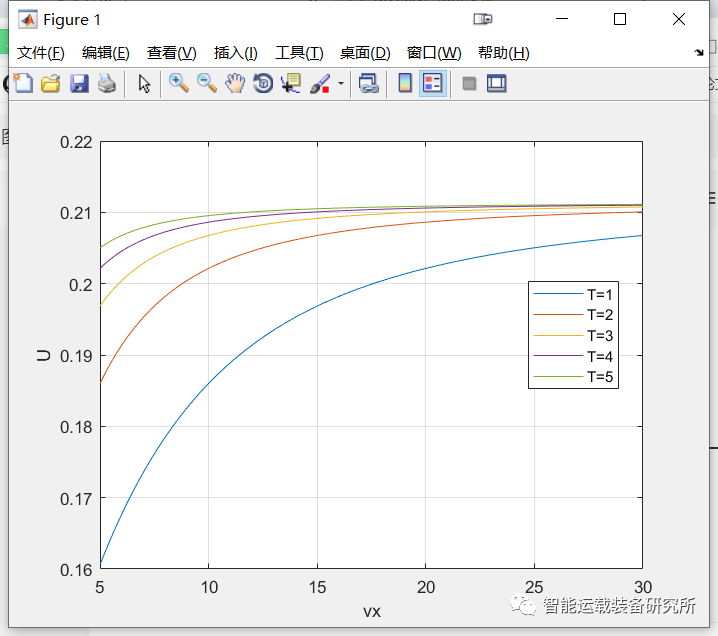
显然0≤U≤1，车辆横摆角速度γd与U的取值有关，为了保证车辆的横向稳定性，其横摆角速度不能太大，需要对最大的横摆角速度进行约束。现在就考虑横摆角速度γd=f(U)的最大值问题。根据KKT原理，最大值将出现在极值点或者边界点。当U=0或者U=1时，车辆横摆角速度γd=0，因此，换道过程中最大的横摆角速度肯定出现在极值点。对横摆角速度γd=f(U)求导可得极值点满足方程
令
则-1/4≤z≤0，且极值点方程被转化成一元五次方程
可以先求解该方程得到z后再求解极值点U。通过分析发现，该方程的解与中间变量a的取值有关，那我们就借助MATLAB工具仿真分析一下该极值点与a取值的关系，程序如下。
clear,clc
T=1:5;%换道时距
vx=linspace(5,30);%车速
U=zeros(5,10);
yend=3.5;
%%
for i=1:5
for j=1:100
xend=T(i)*vx(j)+2;
a=(30*yend/xend)^2;
z=roots([18*a 5*a 0 0 -6 -1]);
index=find(z<=0&z>=-0.25&imag(z)==0);
U(i,j)=min(roots([1 -1 -z(index)]));
end
end
figure
plot(vx,U')
grid on
xlabel('vx');ylabel('U')
legend('T=1','T=2','T=3','T=4','T=5')
%%
u=linspace(min(min(U)),max(max(U)));
fu=u.*(u-1).*(2*u-1)./(1+a*u.^4.*(u-1).^4).^1.5;
figure
plot(u,fu)
grid on
xlabel('U');ylabel('fU')
求解结果如下。可见，当U=0.21时，车辆横摆角速度γd最大。
图3 仿真求解结果
当U=0.21时，最大的横摆角速度为
其中，p=60U(U-1)(2U-1)=5.77，q=900U^4*(U-1)^4=0.68。
因此最大的横摆角速度必须满足车辆动力学限制条件即：
定义风险评估函数为
在实际的车辆避障过程中，为更加有效地评估风险，从而进一步探索安全换道距离的极限位置所在，本文采用了跟随车辆和前车的实时距离。
假设紧急避障的极限安全距离满足如下关系式：
其中，M和N为比例系数。
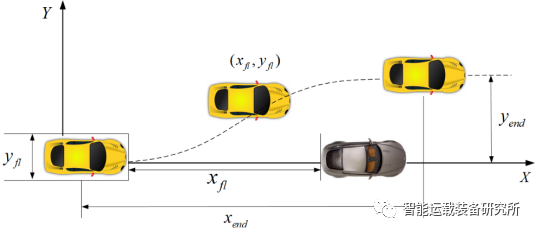
如图4所示的紧急转向避障，其中，xfl为车载传感器（雷达或摄像头）探测到距离前车的纵向距离，yfl是当行驶距离为xfl时的横向位移。
图4 紧急转向避障
假设(xfl,yfl)是无碰撞换道轨迹上的一个点，根据换道轨迹的公式可得M和N之间满足关系式
将其带入风险评估函数中得到改进后的风险评估函数
安全换道过程的风险评估函数需满足F≤0，其对应的极限安全位置恰好对应F=0。此时，本车与障碍物车辆间的纵向距离xfl是自变量N的函数，即F=0相当于隐函数F(xfl,N)=0，换道的极限安全位置是xfl取最小值时，该问题就变成了求解隐函数的极值点N使得纵向距离xfl最小。通过隐函数求导可得其极值点为N=2.2，取N=2，则M=2。则简化后的风险评估函数为
根据F=0可得动态因子为
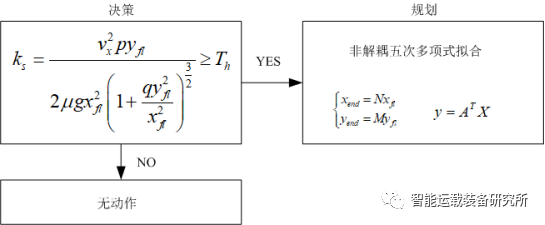
当车辆紧急换道避障时，假设车宽为1.7m，横向安全阈值取0.5m，则yfl=2.2m。根据实际的纵向距离xfl和行驶速度vx实时计算动态因子ks，当Thmin≤ks≤Thmax时即可换道避障，否则存在碰撞或者横向失稳的风险。行为决策过程如下图所示。
图5 行为决策过程示意图
参考文献：Emergency steering control of autonomous vehicle for
collision avoidance and stabilisation
广告
广告
编辑推荐
最新资讯
-
小米4大顶尖技术发布！雷军亲自演示，比亚
2024-11-15 11:43
-
汽车动力性试验实例
2024-11-15 10:52
-
汽车滑行阻力试验综述
2024-11-15 10:52
-
重磅新车抢先看！懂车帝广州车展举办独家新
2024-11-15 10:30
-
MathWorks和恩智浦（NXP）推出基于模型的BM
2024-11-15 09:42
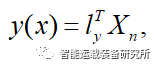
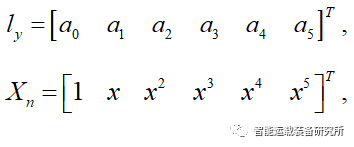
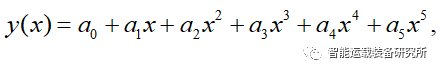
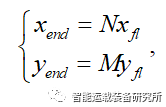
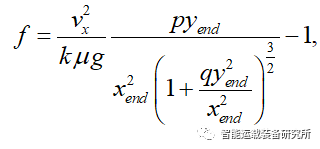
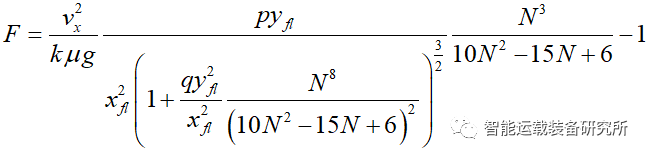
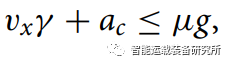
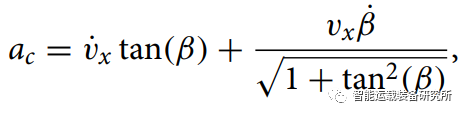
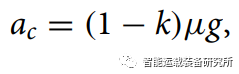
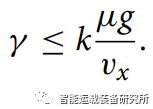
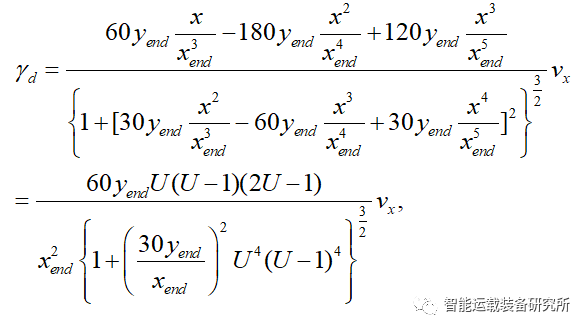
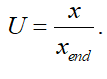
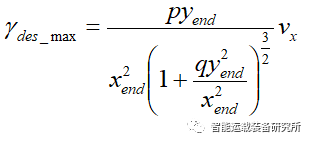
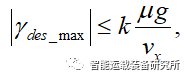
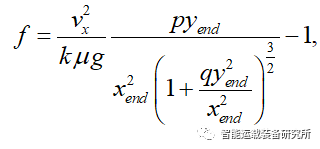
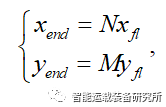
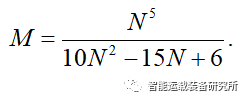
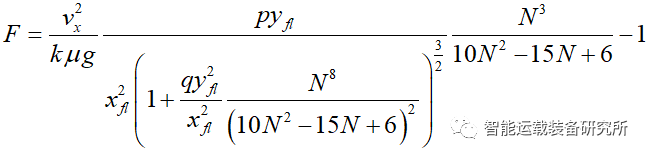
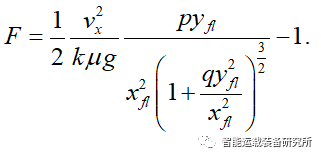
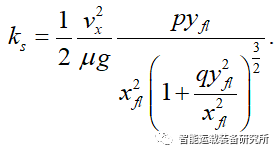
广告
广告
