广告
某车型悬置紧固件断裂问题分析及紧固参数设定研究
2021-11-29 09:43:18· 来源：汽车NVH云讲堂
摘 要：对某款车型悬置紧固件断裂进行分析, 从故障件的宏观及微观角度分析确定了紧固件的断裂模式。建立了悬置支架贴合面滑移量的CAE 分析模型, 经分析现有紧固
摘 要：对某款车型悬置紧固件断裂进行分析, 从故障件的宏观及微观角度分析确定了紧固件的断裂模式。建立了悬置支架贴合面滑移量的CAE 分析模型, 经分析现有紧固参数下存在贴合面滑动风险。结合紧固工艺及实测紧固曲线重新调整紧固参数并通过滑移CAE 模型验证了紧固可靠性，最后通过道路试验证及残余扭矩测试验证了紧固的可靠性。
关键词：悬置 紧固件 断裂 滑移
1 引言
悬置为连接动力总成与车身的零件，其承受由动力总成传递到车身的载荷及由路面冲击引起从车身传递到动力总成的载荷。这些载荷值较大且为交变复杂载荷，其对悬置紧固件的紧固可靠性提出了较高的要求。
随着汽车工业的发展，大扭矩成为高性能车型的重要指标之一，同时混合动力、纯电动等车型可在瞬间输出很大的扭矩，大扭矩便会对悬置连接件产生较大的冲击，同时混合动力总成由于电机的加入其整体重量也有较大增加。扭矩及重量的增加都对悬置紧固效果提出了更高的要求。
悬置紧固件通过施加一定的扭矩从而产生夹紧力，由夹紧力来克服各种冲击力，理论上可以通过载荷计算出所需的夹紧力及扭矩，但由于载荷的复杂性、力传递过程的复杂性、难以准确获取摩擦系数等参数以及拧紧工艺的不稳定性使得计算的难度较大、计算的准确性较低。
本文针对某款车型悬置螺栓断裂故障，从故障件的宏观及微观角度分析确定了紧固件的断裂模式。建立了悬置支架贴合面滑移量的CAE 分析模型, 经分析现有紧固参数下存在贴合面滑动风险。结合紧固工艺及实测紧固曲线重新调整紧固参数并通过滑移CAE模型验证了紧固可靠性，并通过路试验证及残余扭矩测试验证了紧固的可靠性
2 断裂紧固件分析
某车型在道路试验过程中发生悬置紧固件断裂如图1，断裂紧固件包含两颗双头螺柱及1 颗螺栓，其中1# 螺柱、2# 螺栓、3#螺柱分别对应1#、2#、3# 安装孔。
2.1 宏观分析
由图2 可以看出支架与紧固件贴合边缘有明显摩擦痕迹，3 个安装孔内均有螺纹挤压痕迹，因此可以判断紧固件在断裂前已发生了松动，由图1 可见3 个紧固件断口均平齐未见明显质量缺陷，端口呈典型的疲劳断口形貌，由此可初步判断紧固件松动后发生了疲劳断裂。
2.2 微观分析
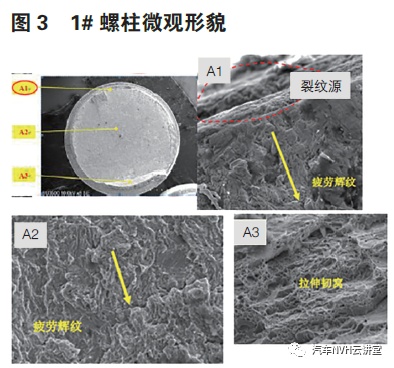
对1# 螺柱断口分进行微观观察，分为A1、A2、A3 3 个区域进行观察发现A1 区域为疲劳源，逐步扩展到A2 区域，最后在A3区域发生了瞬间断裂。
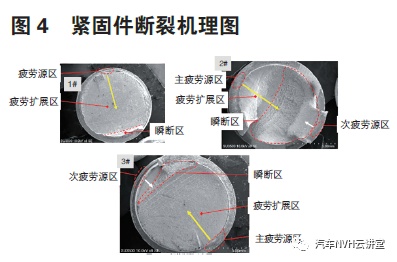
同理对2# 螺栓及3# 螺柱进行分析整理出1#、2#、3# 紧固件的断裂机理如图4，可见1# 螺柱的瞬断面积最小、3# 次之、2# 瞬断区最大，由此可以判断1# 首先发生了疲劳断裂，3# 随后发生了疲劳断裂，2#最后发生疲劳断裂。
3 滑移分析
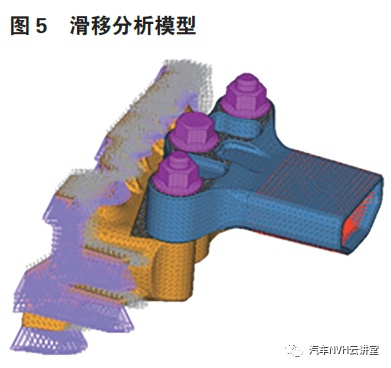
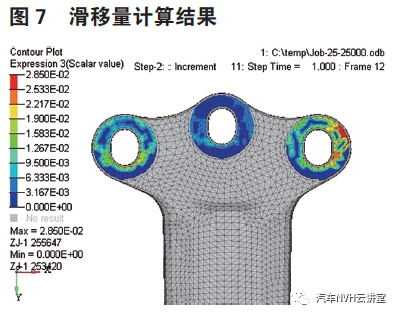
建立悬置支架、紧固件滑移CAE 模型如图5，建立了悬置支架与支架间的接触模型，通过该模型可计算出两个金属支架的相对滑移量从而判断紧固件的夹紧力是否足够，该模型需输入载荷及紧固件预紧力。
3.1 悬置载荷获取
本文采用悬置系统设计校核的常用载荷，即悬置系统28 工况力作为输入力，经计算其中第25 工况力为最易引起滑移的工况，以下计算以第25 工况力作为输入力，力值如表1所示。
3.2 夹紧力获取
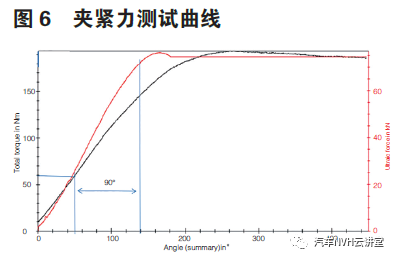
该车型采用的拧紧方式为扭矩法，设定扭矩值为110+/-10N.m，可根据以下公式得到对应的夹紧力，也可根据夹紧力实测曲线如图6 得到，为使夹紧力更贴合实际，本为采用实测曲线进行计算。
其中F0- 夹紧力
T- 扭矩 N.m
K- 拧紧力矩系数
d- 螺纹公称直径，mm
考虑到实际装配后的扭力衰减及统计数据选取扭力值的70% 作为最终扭力，通过图6试验曲线可得出其对应的夹紧力为25KN。
3.3 滑移量计算
将第25 工况力及2.2 得到的夹紧力带入到CAE 模型可计算出滑移量为0.28，滑移值大于目标值0.2，因此现有紧固件扭矩值存在滑移风险。
4 紧固参数设定及验证
根据滑移CAE 模型计算，如需滑移量小于0.2，夹紧力需大于32.5KN，在不更换紧固件及改变连接方式的情况下，现有扭矩法无法实现该夹紧力。
拧紧方式最常用的有扭矩法及扭矩+ 转角法两种，对于扭矩法，为确保紧固件不被损坏，紧固件需工作在弹性区域同时最终夹紧力受摩擦因素影响较大。因此扭矩法存在以下两个特点：1、所提供的夹紧力比较有限；2、受摩擦因素等影响较大导致最终夹紧力散差较大，夹紧力的稳定性不足。
对于扭矩+ 转角法，控制转角实质为控制紧固件的伸长量，因此该方法螺栓可工作在屈服段，同时受摩擦因素的影响较小。因此扭矩+ 转角法存在以下特点：1、相对于扭矩法可以提供更大的夹紧力；2、夹紧力的稳定性较扭矩法更好。
4.1 紧固参数设定
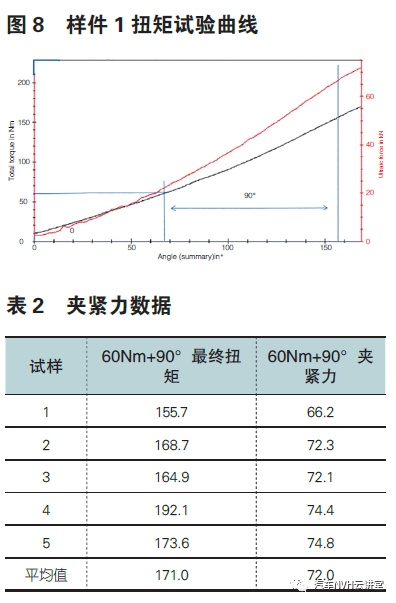
结合图6 夹紧力实测曲线及夹紧力需大于32.5KN, 同时考虑装配工艺的要求设定初始扭矩为60N.m, 转角为90° , 初始扭矩的设定主要考虑支架贴合面要充分贴合, 转角90°为在没有自动设备的情况下也便于控制的角度。对于初步设定扭矩参数60N.M+90°进行5 组扭力试验，样件1 扭矩试验曲线如图8，5 组试验数据见表2。
4.2 紧固参数校核及验证
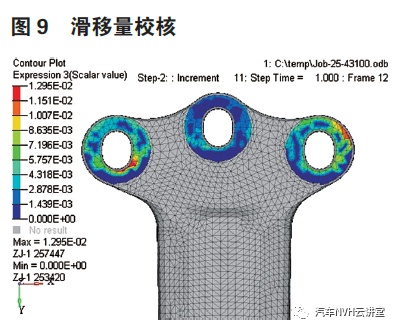
由表2 可知60Nm+90°拧紧参数对应的最小夹紧力为66.2KN，考虑到扭矩及夹紧力的衰减，经统计衰减后的最小夹紧力为43KN,43KN 对应的滑移量如图9，滑移量为0.12 满足小于0.2 的目标值要求。
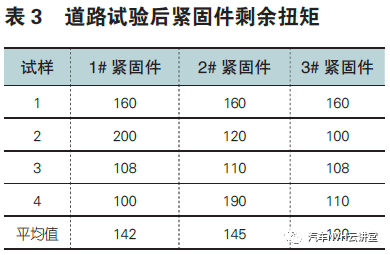
采用60Nm+90°拧紧参数，选取4 台车进行道路试验验证，试验完成未发生紧固件松动及断裂故障，各紧固件的残余扭矩如表3 所。
5 结论
本文从宏观及微观的角度对紧固件断裂故障进行了分析，找出了故障模式，并采用滑移量计算的CAE 模型验证了滑移风险的存在，然后采用理论计算与扭矩实测相结合的方法确定了新的扭矩参数，再次通过滑移CAE 模型验证了新扭矩参数的可靠性，最后通过道路试验对紧固可行进行验证，验证结果表明新的紧固方案紧固可靠。
作者：李聪 张帆 杨玉玲 覃臻 覃丽霜 蒋斌文
作者单位：上汽通用五菱汽车股份有限公司 广西柳州市 545007
来源：时代汽车
- 下一篇：聊聊自动驾驶—高精度地图
- 上一篇：高低压电气架构的发展状态和演变趋势
广告
广告
编辑推荐
最新资讯
-
产品升级 | 全新发动机排放测试系统 一体化
2024-11-06 15:06
-
产品升级 | 全新发动机全流稀释定容采样系
2024-11-06 15:04
-
全新便携式排放测试系统 实际驾驶排放测试
2024-11-06 15:04
-
关于公司名称变更的通知：湖北锐意自控系统
2024-11-06 14:43
-
攻坚气体传感器核心部件国产化，四方光电：
2024-11-06 14:42
广告
广告
