广告
锂离子电池动态加载刚度强化机理研究
2021-12-08 17:01:48· 来源：汽车安全与轻量化 作者：邢伯斌
锂离子动力电池在剧烈碰撞中受到动态挤压失效，现有研究指出锂离子电池在动/静态载荷下的力学特性存在较大差异，然而锂离子电池在高速碰撞下力学行为的主导机制仍不明确。麻省理工学院机械系的朱俊儿博士与清华大学车辆安全与轻量化团队合作研究了锂离子电池的动态加载强化机制。通过试验验证，解析模型分析和有限元仿真验证等手段，证实了黏性电解液在固体骨架的流动造成额外的能量耗散强化了软包电池在动态加载中的结构刚度。该研究为锂离子电池的碰撞安全设计提供了重要理论依据。相关工作已被International Journal of Impact Engineering收录。
前期研究表明[1]，受到动态挤压作用时，正常的锂离子电池相比处于贫液状态的电池获得了更高的结构刚度和更小断裂位移。锂离子电池在不同加载速率下力学响应的差异存在两个潜在来源：一方面，组分材料所展现的应变率效应潜在影响单体的力学特性；另一方面，动态载荷驱动下电解液在固体骨架内流动可能造成额外的能量耗散。理解锂离子电池的动态效应对于提高电池的碰撞安全性能，改善碰撞保护设计十分重要。电池单体在动态挤压中的力学特性变化的主导影响因素仍不明确。
挤压加载过程中单体结构主要受到压缩载荷。本团队基于图1中所展示试验流程开展了电池单体的挤压测试和不同状态的叠层样品的动/静态压缩试验。叠层样品从电池单体中直接裁剪获得，随后通过塑封袋进行封装，确保了叠层样品内部结构充分浸润在电解液环境内。干燥的叠层样品需要充分静置等待电解液完全挥发后，再用于测试。
图1 电池单体动/静态挤压试验测试及叠层样品动态压缩试验示意
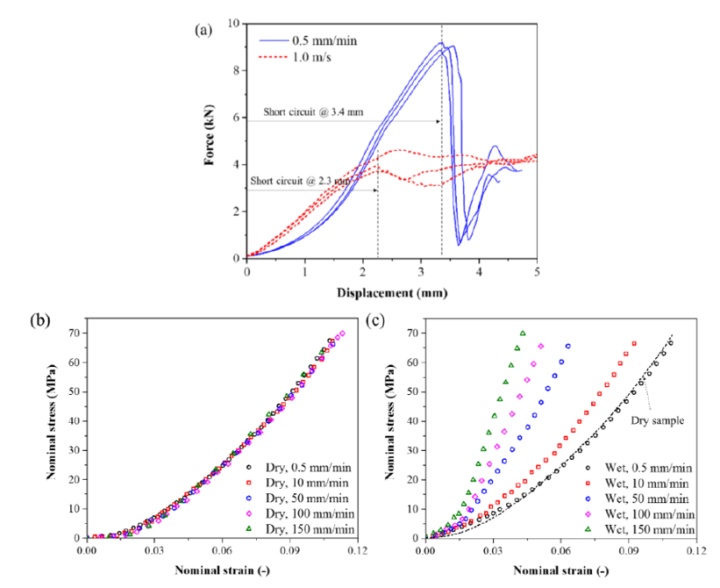
可以看到，电池单体具有比较显著的动态效应，而叠层样品的动态效应完全取决于电解液状态（图2）。干燥的叠层样品几乎不体现出任何的动态效应，所有加载速度下的名义应力-应变曲线几乎重合。充分浸润在电解液环境下的叠层样品在不同加载速率下的压缩测试中展现出了随速度提升逐渐增强的结构刚度，这与单体层级试验中所观察的现象保持一致。富含电解液的叠层样品在0.5 mm/min挤压速度下所展现的响应与干燥叠层样品的压缩机械响应处于相同水平。这些试验结果证实，电解液与固体骨架的流固耦合效应是造成电池单体动态效应的主导因素。
图2 软包电池单体的动态效应试验验证：(a) 电池单体挤压试验，(b) 干燥叠层样品的压缩响应，(c) 富含电解液的叠层样品的压缩响应
通过比较不同电解液状态的层叠样品在不同压缩速率下的力学响应差异，电解液是影响软包电池动态响应的关键要素。由于黏性液体的存在，电池单体的单向压缩过程是一个典型的流固耦合问题：结构变形驱动黏性液体流动，产生额外的能量耗散。基于液体黏性耗散的机理，我们建立了电池结构刚度动态增强效应的解析模型(图3)。平面压缩过程中，叠层样品的体积以恒定速率被压缩，试件内部孔隙率减小驱使电解液向外溢出(图3(a)); 当黏性液体（电解液）流过隔膜材料与活性涂层等多孔材料的微孔隙时，液体黏性耗散需要消耗一部分能量，作为宏观结构响应的压缩应力会大幅增加。
图3 电池单体动态效应解析模型：(a) 平面压缩状态电池结构响应，(b) 电解液-固体骨架基本结构
充分浸润的孔隙结构的整体结构响应是孔隙骨架与电解液的贡献之和，孔隙结构中任意一点的应力通过式(1)描述
其中σij为应力张量，σij*为固体骨架的应力张量，b为毕渥数(biot coefficient)，pf为电解液孔隙压力，δij为克罗内克函数。毕渥数b通过多孔骨架与非多孔颗粒的体积模量决定。固体骨架的力学特性可以借助本团队所使用的Drucker-Prager/Cap模型较好的描述[2]。电解液的孔隙压力通过Darcy定律描述，实现了压力梯度与电解液流速之间的关联。考虑到测量活性涂层孔隙率渗透率较为困难，流体渗透率与多孔结构中孔隙率关系按Kozeny-Carman经验公式估算。详细的公式推导和所使用的材料参数可以参考论文内容。
随后基于一系列假设，单向压缩状态下电池结构的流固耦合解析模型可直接被求解：
(1) 电池结构的塑性泊松比几乎为0
(2) 电解液仅仅存在于多孔隔膜和活性涂层材料区域
(3) 次级颗粒为不可压缩
(4) 电解液材料特性在所研究的加载速度范围内保持不变
(5) 基于一维变形假设，压缩方向的压力可以直接由式(1)简化为式(2)
考虑到流体孔隙压强随半径变化，压缩方向上的宏观载荷平衡关系可以由式(3)表达：
综合考虑如上假设条件后，平均压缩应力可以写为
式（4）对于所研究的加载速度范围内的动态加载响应均给出了较为合理的预测值，证实了解析模型以及液体黏性耗散机理的正确性（图4）。根据解析模型可知，电解液导致的额外压缩载荷与压缩速率成正比。因此，当压缩速率较小时（0.5 mm/min），电解液耗散导致的额外压缩载荷几乎可以忽略，湿状态样品与干状态样品的压缩响应基本一致。
图4平面压缩工况中解析模型预测与实际响应对比
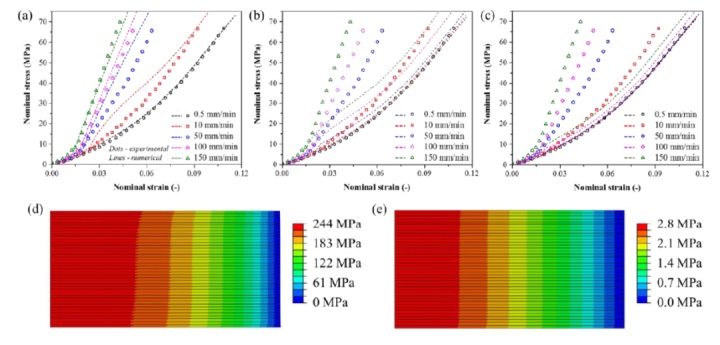
此外，我们在Abaqus/Soils软件中同样建立了满足孔隙力学原理的有限元模型，用于表征电池单体的动态加载结构刚度强化效应。该有限元模型的数值结果由于孔隙介质的渗透率κ的取值确定，而渗透率主要由颗粒直径Dp决定[3]。作为多层结构的正极活性涂层次级颗粒尺寸一般在10 μm, 初次粒子的尺寸一般在1 μm。相似的，负极活性涂层次级颗粒往往是由0.5 μm大小的初级颗粒组成的。图5(a-c)比较了不同颗粒尺寸的孔隙介质有限元模型对于不同加载速度的单向压缩仿真结果。当正极颗粒尺寸为1.0 μm和负极颗粒尺寸为0.5 μm时，仿真模型可以获得较好的仿测对比结果。使用较大的颗粒尺寸时（正极颗粒尺寸10.0 μm和负极颗粒尺寸5.0 μm），动态加载中电解液的黏性能量耗散较为有限，导致电池结构的动态效应不太明显。这与之前的解析模型预测结果有一定出入。解析模型和仿真模型的差异主要在于解析模型简化了电解液流速在各个多孔组分材料内的分布情况。在仿真模型中电解液的流动导致了压缩方向上实际存在孔隙压力梯度。如图5(d-e)所示，相比起0.5 mm/min加载速度，高速加载（150 mm/min）在电池结构内部造成了较大的压强梯度。考虑到精细化模型自身的复杂性，我们可以认为现有的仿真模型已经捕捉到可以满意的动态加载刚度增强效应。
图5 电池单体的孔隙力学仿真模型描述动态效应：(a) 使用初级颗粒尺寸的名义应力-应变响应，(b) 使用中等颗粒尺寸的名义应力-应变响应，(c) 使用次级颗粒尺寸的名义应力-应变响应，(d) 使用初级颗粒尺寸时，0.5 mm/min加载速度对应的孔隙压力，(e) 使用初级颗粒尺寸时，150 mm/min加载速度对应的孔隙压力
Zhu J.*, Luo H., Li W., Gao T., Xia Y.*, Wierzbicki T. Mechanism of strengthening of battery resistance under dynamic loading. International Journal of Impact Engineering. 2019, 131, 78-84
参考文献：
[1] T. Kisters, E. Sahraei, T. Wierzbicki. (2017). Dynamic impact tests on lithium-ion cells. International Journal of Impact Engineering, 108: 205-216.
[2] J. Zhu, W. Li, T. Wierzbicki, Y. Xia and J. Harding. (2019). Deformation and failure of lithium-ion batteries treated as a discrete layered structure. nternational Journal of Plasticity, 121: 293-311.
[3] B. Wu, W. Lu. (2016). Mechanical-Electrochemical Modeling of Agglomerate Particles in Lithium-Ion Battery Electrodes. J Electrochem Soc, 163(14).
广告 
广告
编辑推荐
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
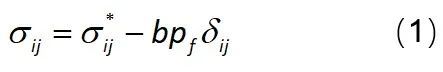
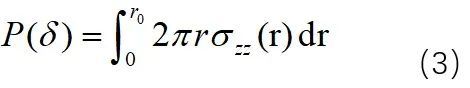
广告
广告
