广告
后缘锯齿对天窗抖振降噪的数值研究
2021-12-10 19:56:15· 来源：AutoAero
摘要本文对天窗降噪进行研究。抑制噪声的策略之一是将撞击天窗后缘的强涡流分解为较小的涡流。这篇文章研究了锯齿天窗尾缘与正弦轮廓波长对抖振降噪的效果。采用
摘要
本文对天窗降噪进行研究。抑制噪声的策略之一是将撞击天窗后缘的强涡流分解为较小的涡流。这篇文章研究了锯齿天窗尾缘与正弦轮廓波长对抖振降噪的效果。采用一系列波长和振幅的正弦曲线组合以研究尾缘锯齿对降噪的影响 ，本研究采用通用汽车模型，以直后缘为基线。结果表明，后缘锯齿对车内声压级有显著影响，对抖振频率的影响可使声压级降低10~15 dB。此外，瞬态流场可视化和涡量等值线证实了锯齿尾缘将大脱落涡分解为小涡流。因此，舱内的声压级得以降低。此外，本文还研究了尾缘锯齿在不同流速下的有效性。结果表明，后缘锯齿策略是降低汽车天窗抖振噪声的有效方法。
引言
天窗噪声是一种非常重要的空气动力噪声源。天窗上方的强剪切层、前缘产生的涡流撞击天窗后缘是与噪声产生有关的主要原因。抖振噪声是天窗噪声中最常见的噪音问题。它通常发生在天窗上方剪切层的瞬态特性能够激发车厢的亥姆霍兹模态，导致剪切层的自持续振荡时。经过多年的数值、实验和理论研究，抖振现象具有低频、高强度的特点。然而，在获得车辆的物理模型之前，很难准确预测特定车辆的抖振噪声有多严重。为了避免进入的气流直接冲击后缘并减弱抖振噪声，许多汽车制造商通常在天窗前缘上游采用一种被称为偏转板的被动控制装置作为最常用的策略。它有效地降低了低频噪声，但在从导流板顶部边缘脱落的分离剪切层中产生了高压波动。当车辆高速行驶时，这样一个额外的偏转板会造成严重的宽带噪声问题，当车辆倾斜时，也会导致更高的阻力。
从以往的文献中可以看出，大部分的被动控制策略都是在天窗的前端采用的。而抖振噪声主要产生在天窗后缘附近区域。本文设计了一种锯齿形天窗后缘结构，以克服在天窗前缘附近设置偏转板以减少抖振噪声的缺点。事实上，边缘锯齿在降噪中的作用已经被许多研究者研究过了。Narayanan等人使用锯齿型翼型前缘来减少翼型前缘与撞击湍流之间的相互作用。他们发现，前缘振幅对提高在平板和翼型降噪水平有很大影响。Hersh等还观察到，前缘的锯齿形成涡旋，减少后缘附近周期性波动力产生的噪声，使速度波动由周期性变为随机。这些研究表明，车顶边缘锯齿可以作为一种有效的减少车顶抖振和宽带噪声的方法。
随着高速计算机技术的快速发展，CFD技术已成为预测汽车模型的气动和声学性能的一种基本有效的方法。精确估计抖振和宽带噪声需要精确预测复杂的瞬态行为(例如，在天窗上方的剪切层中涡旋的形成、脱落和破裂)。在本研究中,当气流冲击天窗的下游边缘时,研究了后缘的锯齿形正弦曲线,其波长(λ)和振幅(h)有三种组合,用于降噪。并进行分离涡模拟(DES)，为全面分析提供详细的流场。
数值方法
1.汽车计算模型
图 1.汽车计算模型示意图
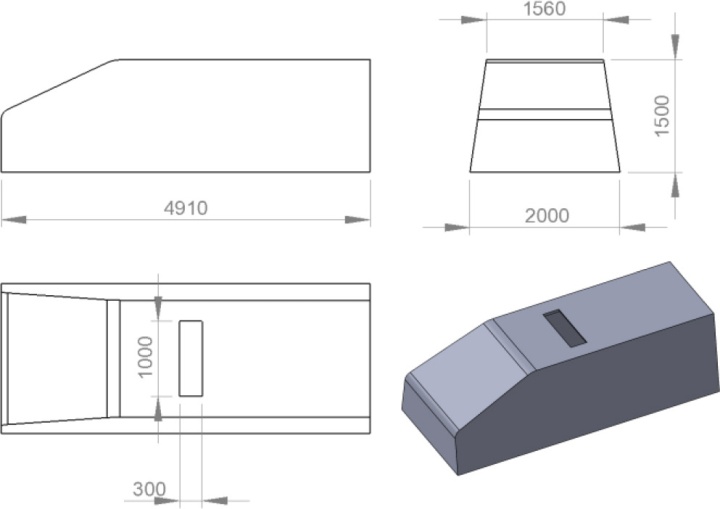
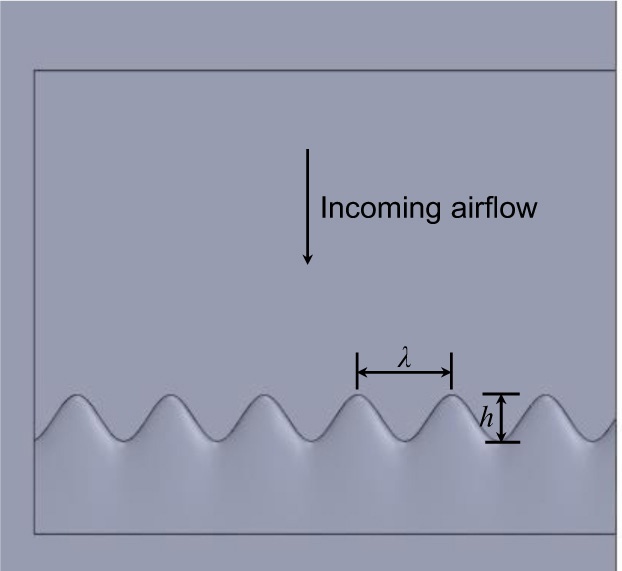
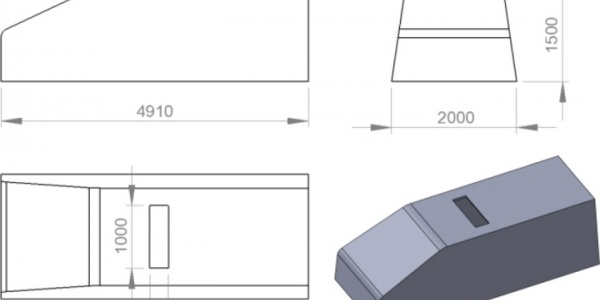
由于实际车辆设计非常复杂，本计算研究采用如图1所示的简单车辆模型。该计算车辆模型的车身长度(L)为4910 mm，高度(H)为1500 mm，顶部宽度(W)为1560 mm，底部宽度为2000mm。目前仿真中没有侧镜，模型与地面之间也没有间隙。图2显示了在形状设计中使用的正弦锯齿的示意图，其中h表示波幅，λ是波长。在本研究中，波幅值(h)保持不变，并构造了h=0.5λ、h=λ和h=2λ三种组合来计算波长变化的影响。
图2. 在天窗后缘上使用的正弦锯齿示意图
2.计算设置
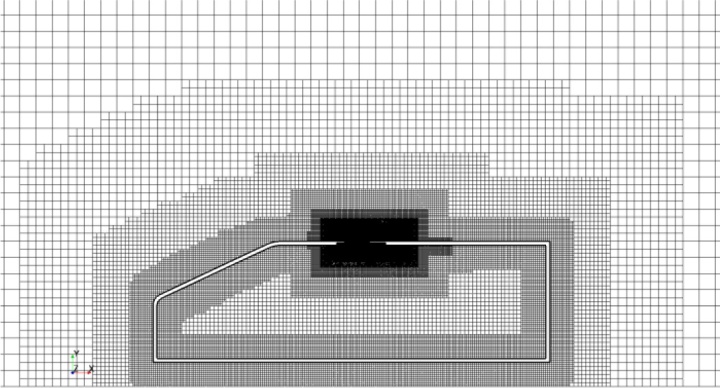
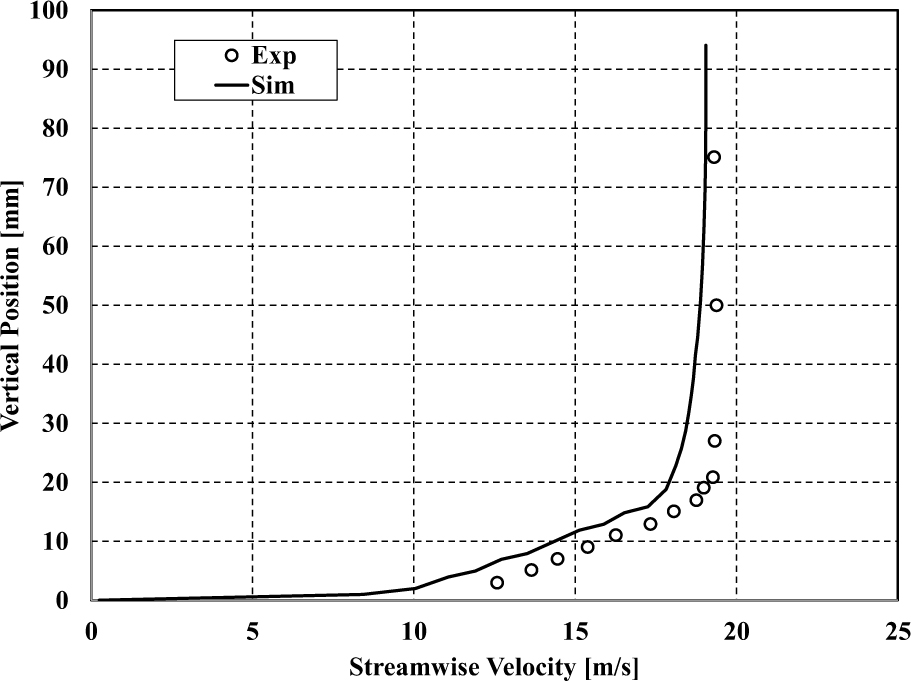
本研究使用了一个结构差异较小但计算设置相同的汽车模型来验证Huco[8]的实验。使用商业CFD代码Star-CCM+生成网格，模拟车辆模型上的流动。这里的气动声学分析是通过非定常计算进行的，因此需要优化网格和设置，以捕获仅在本研究中相关的噪声源和频率。由于车辆几何结构在展向上是对称的，为了减少网格尺寸，避免长时间计算，在计算模型中选择了半车辆模型。一个由大约68.3x10^6个结构单元组成的计算网格被生成以获得所需的分辨率。在开放腔周围区域采用带有2mmx2mmx2mm的网格，以确保捕获频率高达3kHz的湍流噪声源和传播声学高达8.5kHz的精度。从车辆表面以1.3的生长比率生成10个棱柱层，以捕捉边界层的流动特性。所有计算单元在车辆表面的正常分辨率低于y+=1。图3展示了中间对称平面上的计算网格。
图3. 中间对称面上的网格示意图
入口边界延伸至车辆前表面上游4 L。进入气流的速度有两种:20 m / s和30 m / s,分别代表在城市和高速公路上行驶的车辆。下游压力出口位于距车背面约8 L处。为避免反射效应(累积误差），在侧面和顶面远场边界上采用对称边界条件。
本模拟研究采用两种方法。虽然雷诺平均Navier-Stokes (RANS)模拟已经成功地应用于预测车辆周围的许多部分流动，但其捕捉噪声能力有限。因此，本研究采用SST k-ω DES，其结合了边界层RANS模型和非定常分离区域大涡模拟(Large Eddy Simulation, LES)模型的特点，以获得流场中更重要的特性。稳定的RANS结果为DES计算提供了一个完整的初始流场。为了计算气动声学特性采用Ffowcs Williams-Hawkings (FWH)模型获得了指定位置的舱室噪声声压级谱。
结果和讨论
1.计算模型验证
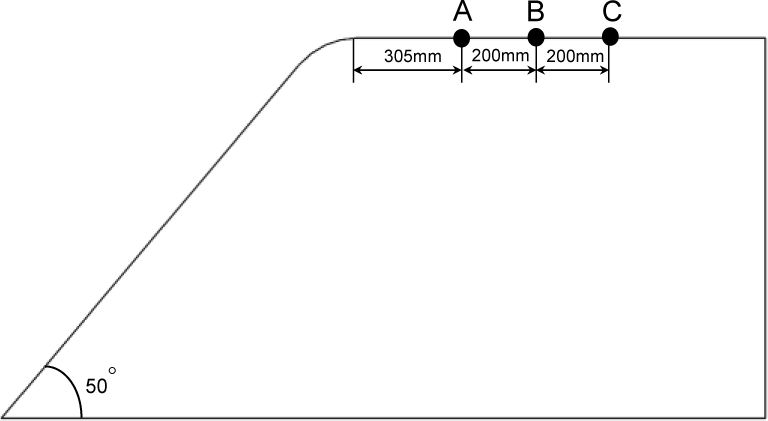
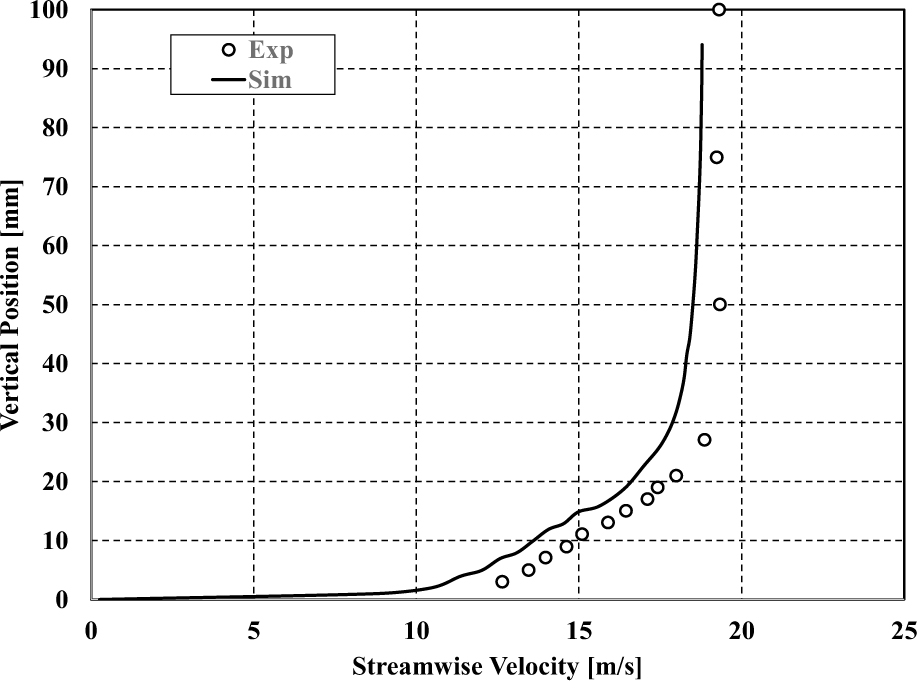
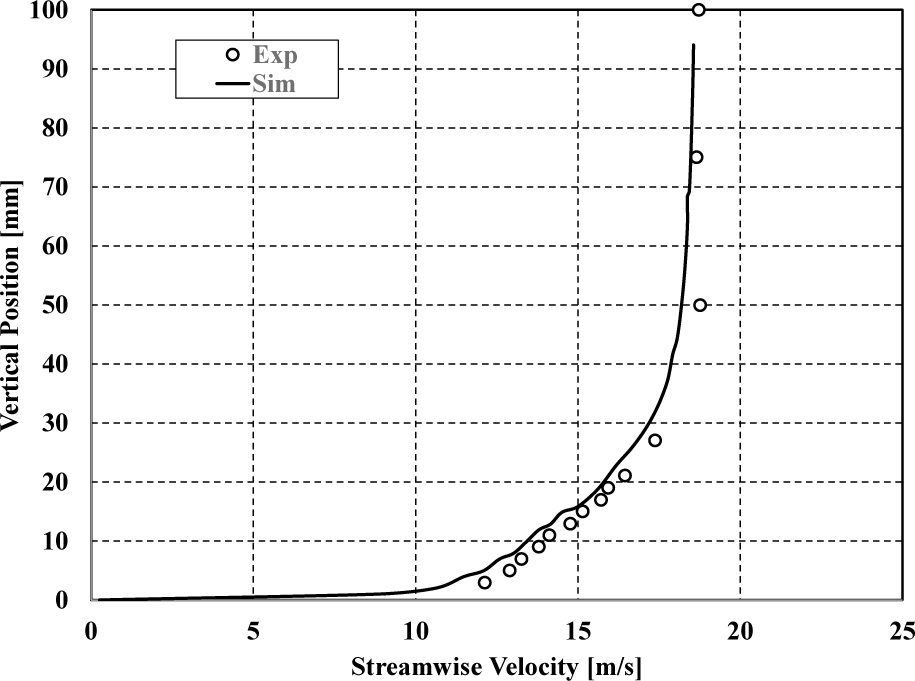
在用于验证的实验测试中，在车辆顶部表面的三个探头位置(探头A，探头B和探头C)测量了流向速度剖面，如图4所示。应该指出的是，试验中使用的入口速度为60公里/小时，天窗为测量而关闭，车辆形状与本次模拟中使用的车辆模型具有类似的配置。速度剖面计算是基于在当前数值模拟中相同位置的时均DES数据。图5显示了模拟结果与实验测量结果的对比。x轴表示绝对流速度和y轴表示距离车辆顶部壁面。结果表明，边界层和外核心区的流动速度分布与各测点的实验结果吻合较好。这确保了该计算研究中的网格足够捕捉详细的流动特征。
图 4.速度剖面的测量点位置
a. A点速度剖面
b. B点速度剖面
c. C点速度剖面
图 5. 监测点位置流速对比
3.结果和分析
当风速为30m/s时
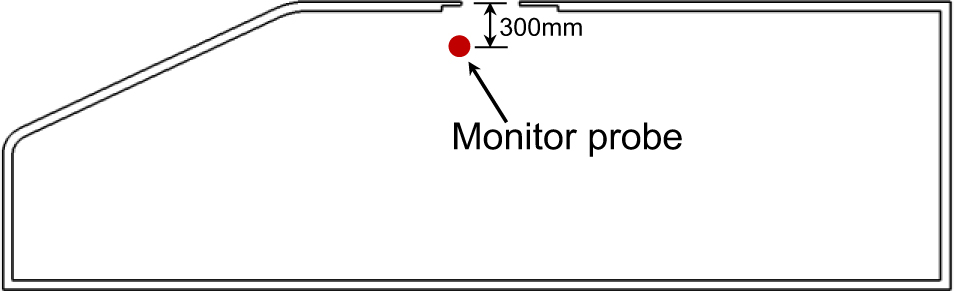
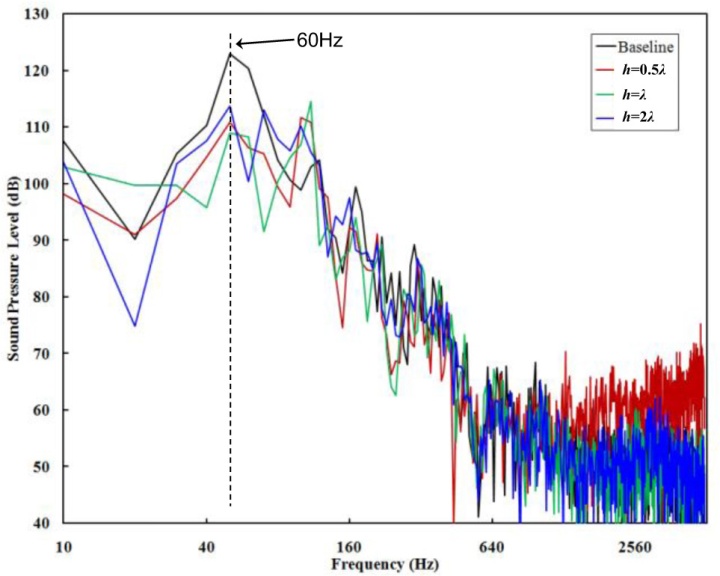
根据Kumar和Mendonca的研究，天窗抖振的峰值频率主要取决于风速和车辆内部几何形状。为了捕捉抖振频率，如图6所示的监测探头放置在天窗前缘下方，对应驾驶员右耳在客舱的位置，获取声学数据。图7给出了在30m/s入射速度下，计算得到的不同车辆设计的声谱，抖振噪声的峰值频率在60Hz左右，且观察到尾缘锯齿的设计至少衰减与基线情况相比，峰值频率为10dB。如上所述，边缘的锯齿几何形状有利于将大涡流分解为小涡流，因此在这些改进的设计中发现了几个较小的峰值，而不是在基线模型中只存在一个峰值频率。除抖振峰值频率外，在频率为25Hz时，h=2λ时的声压级降低约15dB。 在所有修正模型中，具有h=2λ边缘锯齿的设计具有最好的效果。虽然h=0.5λ的情况下的噪声水平在抖振频率具有相似的幅度，但在高频情况下，它的噪声水平高于其他两种情况(f >1000赫兹)。
图 6. 监测探头的位置
图 7. 不同后缘在监测探头位置的声压级对比
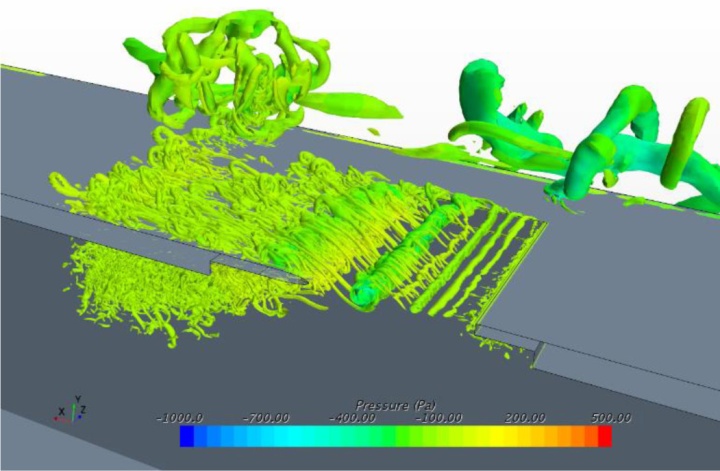
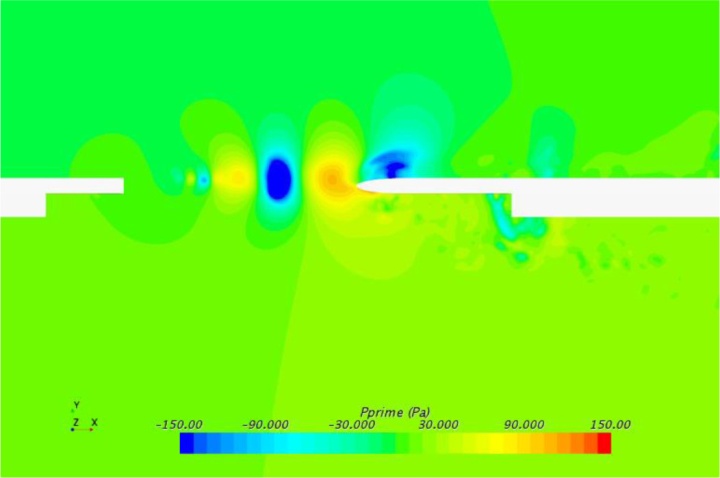
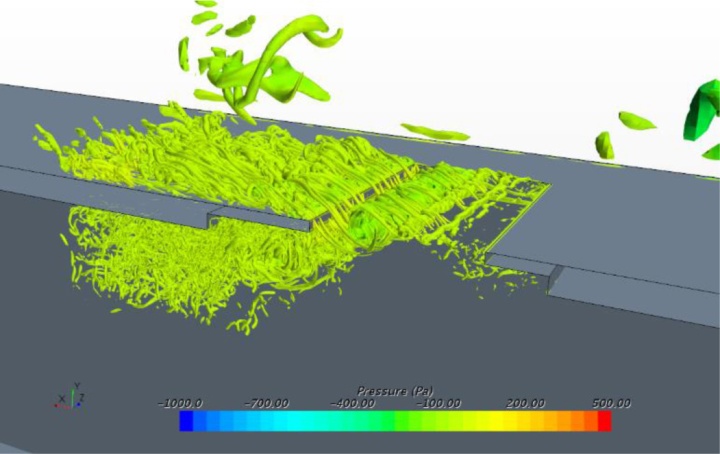
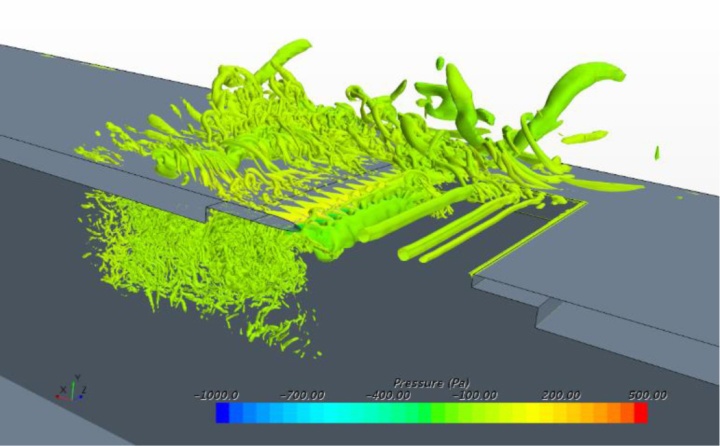
为了找到可以用来降低噪声水平的边缘锯齿背后的原因，需要仔细检查详细的流场。图8显示了Q准则的三维流体结构，其用识别旋涡核心的一个标量着色，即流动压力（hydrodynamic pressure)。虽然在接近天窗前缘的区域可以发现基线情况和修改情况之间的微小差异，但在接近天窗后缘的区域可以发现显著的偏差。从天窗脱落的大涡流冲击后缘，然后分解成一系列小涡流。它们被后缘分成两部分:1)上旋涡随着主流在车外移动，2)下旋涡核心留在车内。在改进的设计中，从上游前缘脱落的涡流被这些锯齿状的后缘分解成更小的涡流结构。在h = 0.5λ和h = 2λ的情况下，上层涡明显受到抑制，而在h = λ的车辆模型中，下层涡明显受到抑制。在基线情况的舱室内涡芯中观察到较高的流动压力。
a. 基线
b. h = 0.5λ
c. h = λ
d. h = 2λ
图 8. 压力Q准则等值面
由于噪声本质上是由压力波动产生的，因此研究压力波动与天窗噪声产生的关系非常重要。压力波动(p ')可定义为 ：
其中p为流动压力，N为快照次数。
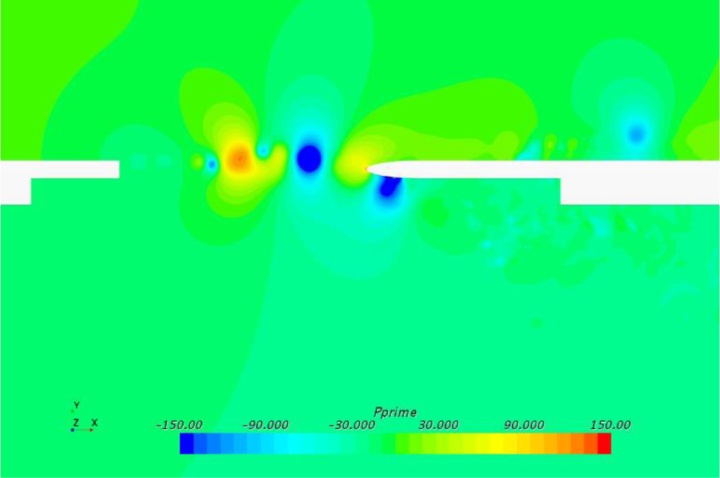
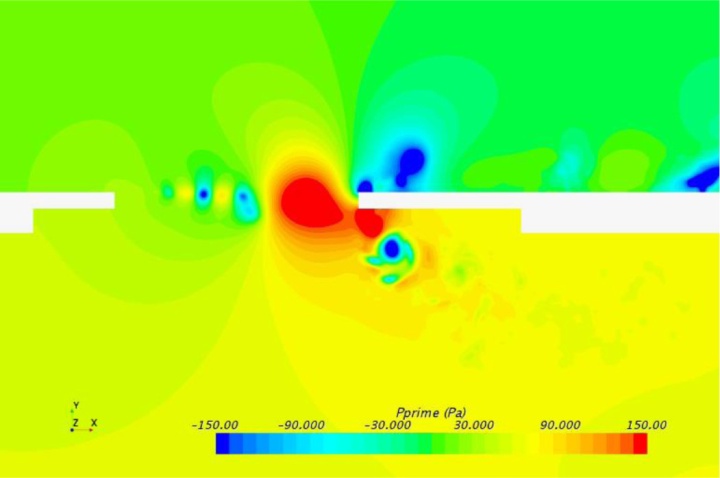
图9显示了天窗附近区域的压力波动。需要注意的是，该非定常脉动压力只包含流动压力，不包含声学信息。在基线情况下，在天窗后缘附近和舱内观察到较大的压力波动。当使用锯齿形天窗后缘时，这种波动得到了抑制，尤其是在车辆客舱内。
a. 基线
b. h = 0.5λ
c. h = λ
d. h = 2λ
图 9. 天窗附近区域的压力波动
当风速为20m/s时
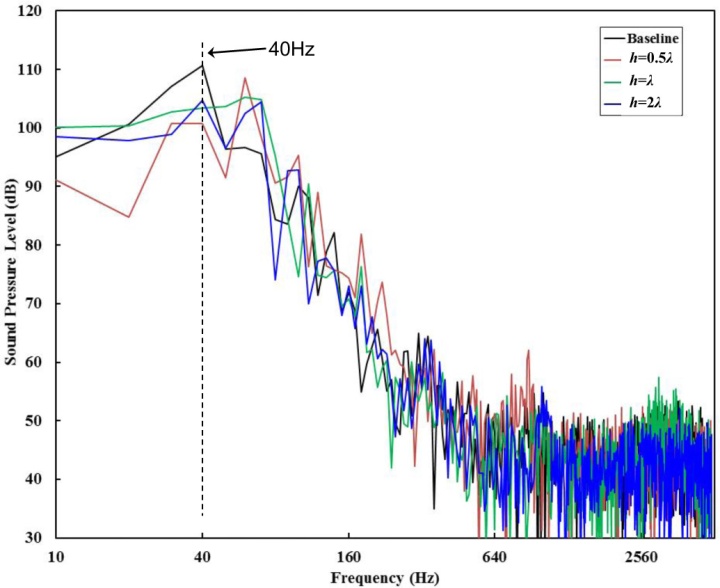
为了研究尾缘锯齿在低速下的影响，将进气道的自由流速度减小到20m/s。 图10给出了图6所示的同一监测探头在频域的计算声压级。如前所述，抖振峰值频率会随着来流风速的减小而逐渐减小，基线情况下20m/s自由流的峰值频率在40Hz左右，即比自由流速度为30m/s时低20Hz。后缘锯齿车辆模型的抖振声压级振幅也低于基线情况。装备 h = λ和h = 2λ的锯齿形状的汽车模型可以降噪6分贝。虽然h = λ的情况下的噪声水平在抖振频率有10dB的降低，但在60Hz左右的频率有比其他两种配置更高的声压级。综合考虑，h = λ的锯齿形是三种构型中最佳的选择。此外，可以看到，随着自由流速度的降低，基线与修正模型之间的声压级差异逐渐减小。
图 10. 不同后缘在监测探头位置的声压级对比
图11为自由流速度为20m/s时，压力Q准则的等值面。这些图中所示的涡流结构与图8所示的模式相似，但由于来流速度的减小，涡流强度比前面所示的要弱。在基线情况下，直尾缘会产生更多的涡流，这将会导致更高水平的噪声产生。
a. 基线
b. h = 0.5λ
c. h = λ
d. h = 2 λ
图 11. 压力Q准则等值面
总结和结论
本文在一个简单的汽车模型上，在天窗后缘采用三种锯齿形状来减少抖振噪声的产生。为了获得准确的流场和声场，进行了全面的DES和气动声学研究。
结果表明，所提出的边缘锯齿设计能有效地降低抖振噪声。当车顶边缘锯齿形为h = λ时，在30m/s的自由流速度下，抖振峰值频率的最大声压级降低幅度可达10 dB以上，在20m/s的自由流速度下，抖振峰值频率的最大声压级衰减约为6dB。研究发现，与基线车辆相比，这些经过修改的算例舱内的压力波动明显减弱。当气流撞击锯齿状后缘时，湍流旋涡被显著抑制。此外，随着自由流速度的降低，抖振峰值频率降低，基准情况与修正模型之间的声压级差也会减小。将后缘修改为锯齿形后，天窗周围涡强度显著降低，表明后缘锯齿形可以有效降低天窗抖振噪声。
文献来源：Wang Zhenyu,Zhuang Mei. A Numerical Study of Trailing Edge Serrations on Sunroof Buffeting Noise Reduction[J]. SAE International Journal of Vehicle Dynamics, Stability, and NVH,2017,1(2): 112-118.
AutoAero是吉林大学张英朝教授团队建立的专业汽车空气动力学微信公众号号，致力于普及汽车空气动力学知识，传播汽车空气动力学。推广包括流体力学基本理论，汽车空气动力学及热管理水管理等基础知识，乘用车气动造型设计，卡车气动造型设计，风洞实验技术等多方面的内容。欢迎有兴趣的专业人士阅读、关注、共享！
广告 
广告
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
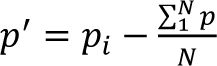
广告
广告
