广告
浅谈汽车电子振动相关理论
2021-12-15 23:23:38· 来源：汽车测试网
一：共振的相关概念振动试验对很多工程应用人员来说，既熟悉又陌生！熟悉是因为我们的产品经常需要做振动试验，可谓是天天见；然而虽然天天见，但是其中的原理和
一：共振的相关概念
振动试验对很多工程应用人员来说，既熟悉又陌生！熟悉是因为我们的产品经常需要做振动试验，可谓是天天见；然而虽然天天见，但是其中的原理和背后的数学物理理论又让人感觉晦涩难懂，极为抽象，难以把握其精髓。下面笔者就这些尝试做深入浅出的探讨，以期帮助每一位工程应用人员具象理解这些。
首先谈几个概念。
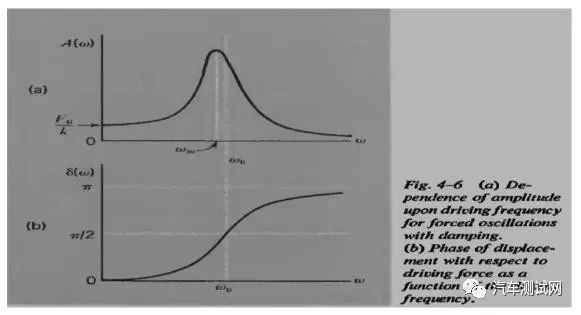
共振和共振频率：激励力施加在一个系统上，激励力的激励频率接近系统的固有频率时，即使这个激励力的量值很小，也能导致系统振动的幅值非常大，这就是所谓的共振现象。下图是当激励频率达到系统固有频率时，发生共振的幅值和相位图示。这时这个发生共振时的频率称之为共振频率。
【幅值相位图】
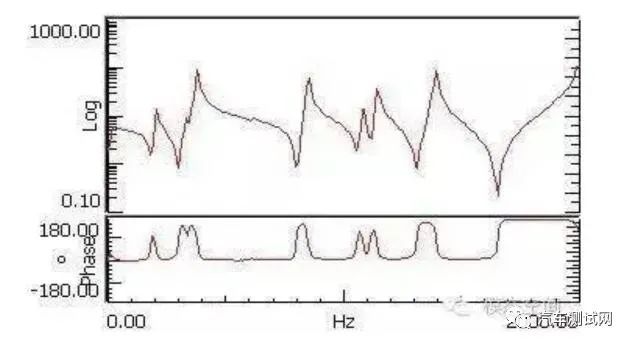
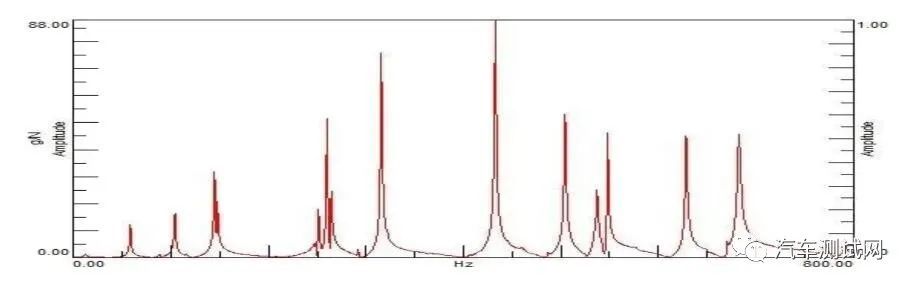
共振峰和反共振峰：在频响函数曲线中，共振频率所对应的峰值称之为共振峰，在这个峰值处，对结构施加很小的激励能量，结构就会产生非常大的振动。当以 dB 形式显示频响函数时，会发现 FRF 曲线中有向下的峰值，这些峰值称为反共振峰。如下图所示：
【共振峰和反共振峰】
频响函数：Frequency Response Function(FRF)是结构的输出响应和输入激励力之比。同时测量激励力和由该激励力引起的结构响应（这个响应可能是位移、速度或加速度）将测量的时域数据通过快速傅里叶变换（FFT）从时域变换到频域，频响函数最终呈现为复数形式，包括实部和虚部。或者是幅值和相位。
【频响曲线】
固有频率：结构系统在受到外界激励产生运动时，将接近特定的频率发生自然振动，这个特定的频率被称之为结构的固有频率，通常一个结构有很多个固有频率。固有频率和外界的激励没有关系，是结构的一种固有属性，不管外界有没有对结构进行激励，固有频率都是存在的。
固有频率又分为无阻尼固有频率和有阻尼固有频率。通常一般系统的阻尼比小于 10%，所以阻尼对结构的固有频率影响不大。
固有频率的阶：结构的固有频率有很多阶，“阶“跟什么有关系呢？在理解阶之前，要先理解与’’“阶”紧密相连的名词“自由度”。自由度是指用于确定结构空间运动位置所需要的最小、独立的坐标个数。空间上的质点有三个自由度，分别为三个方向的平动自由度；空间上的刚体有六个自由度，分别为三个平动、三个转动自由度。一个连续体上实际有无穷多个自由度。有限元分析时将连续的无穷多个自由度问题离散成为离散的有限多个自由度问题，此时结构的自由度也就有限了。因此，一个自由度对应一阶固有频率。
【多阶固有频率】
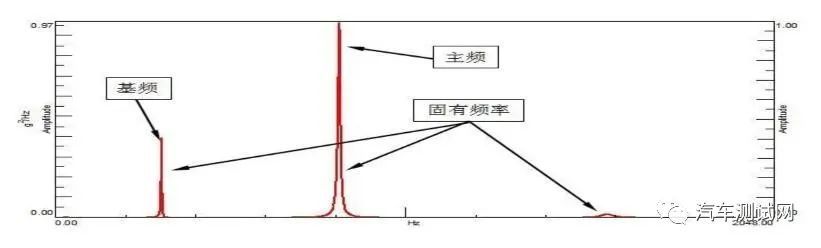
最低阶固有频率：通常称之为基频。跟结构和材质有关。材料的质量或密度越大，结构的基频越低。现实当中，越低阶固有频率越容易被外界激励起来。因而，虽然结构有无穷多阶固有频率，但很多情况下只关心结构一些较低阶固有频率。
主频：结构发生共振时，通常不会以某一个频率振动，而是有多个振动频率，在这些振动频率中，能量最大的振动频率称为主频。
【主频，基频图示】
避免共振，激励频率需要远离固有频率多远？
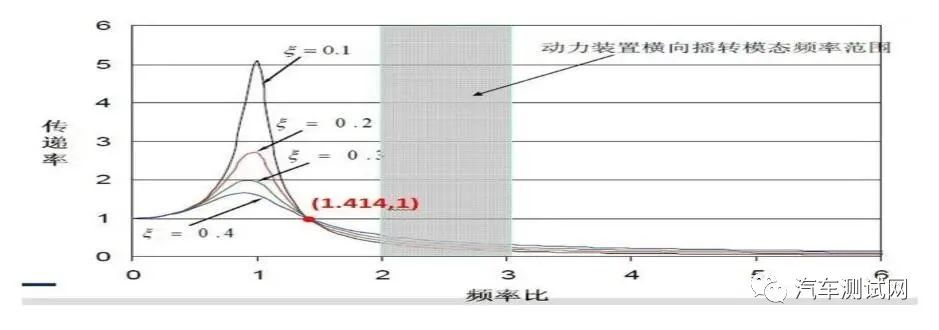
参考下图，纵轴为传递率，横轴为激励频率与固有频率之比。从图中可以看出，传递率等于 1时，对应的激励频率与固有频率之比为 1.414.因此，只有当激励频率远离固有频率 40%以上时才能起到避免共振的作用。但是很多情况下，以考虑 40%以上的频率间隔，似乎是不现实的，因此很难给出一定具体的数字来确定到底应该远离固有频率多远的距离。
二、随机振动相关概念
振动这一物理概念其实在高中的时候就有学习过，但是这些转化成周期性的或者不确定性的信号论时，用到大学课程中那些信号与系统，自动化控制理论中的各种变换时，很多小伙伴们就会觉得摸不着头脑，下面笔者就尝试从一些角度帮助大家理解这些内在的逻辑。
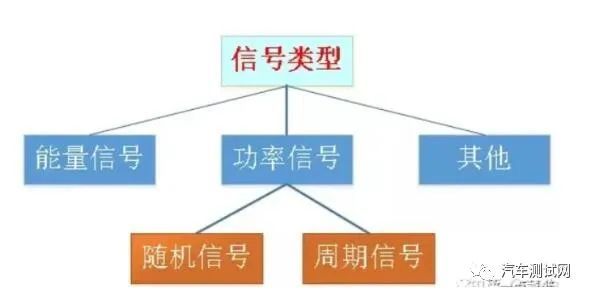
在正式介绍之前先说下信号的分类：在日常工程实践和应用中，使用的信号分类可以大致分为
以下几种：
能量信号：能量有限信号。顾名思义，它是指在负无穷到正无穷时间上总能量不为零且有限的信号。典型例子：脉冲信号。
功率信号：功率有限信号。它是指在在负无穷到正无穷时间上功率不为零且有限的信号。典型例子：正弦波信号，噪声信号。功率信号还可以细分为周期信号（如正弦波信号）和随机信号（如噪声信号）。
对能量信号和周期信号，其傅里叶变换收敛，因此可以用频谱（Spectrum）来描述；对于随机信号（实际的信号基本上是随机信号），傅里叶变换不收敛，因此不能用频谱来描述，而应当使用功率谱密度（PSD）。说到这里大家就应该比较明白了，通常我们的振动控制软件上，为什么正弦振动的时候可以用频响传递函数幅值比和相位谱来分析正弦振动了，而随机却只能用功率谱密度来定义随机振动了。
关于随机振动这里再插入一段描述帮助我们理解这个随机信号：生活中，我们看到太阳光照射会产生热量，其实太阳光就是各种不同波长频率的电磁波混合而成，如果我们用一个三棱镜就可以很清晰的把太阳光分解成不同成分的电磁波了，这些电磁波的能量会对体做功(电磁波激励物体分子震荡)，使物体发热。
有了上面的背景介绍后，我们对随机信号大致有个直观的认识了，下面就再深入讨论随机振动。
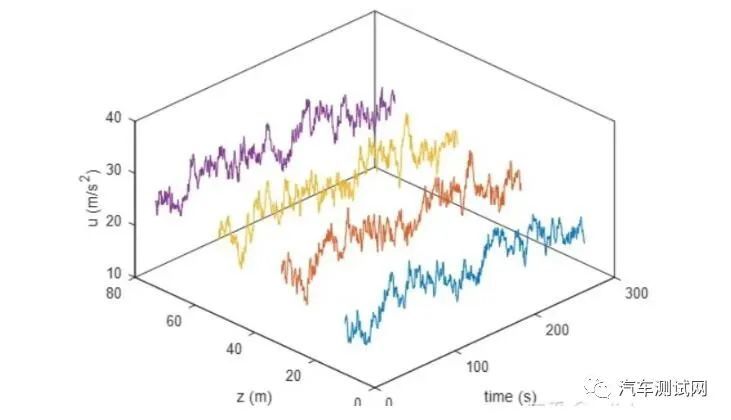
随机振动：是因为振动源是随机信号，顾名思议，就是信号的发生带有随机性，无法用一个明确的函数把它表达出来，一个典型的随机信号大概长这个样子：那这样一个随机杂乱无章的信号我们要怎么来描述它呢？
随机信号和正态分布有什么关系？
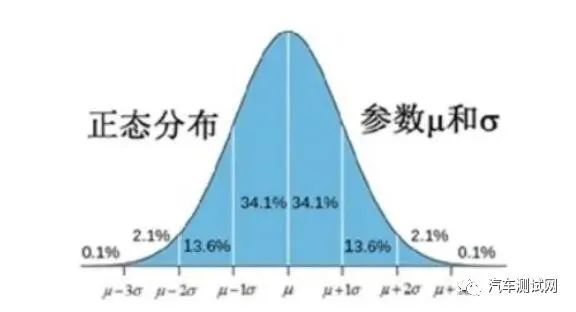
经过多名科学家们的验证，这里只给出结论：大量相互独立的随机变量，其平均值正态分布；也就是说：在一定条件下，各种随意形状概率分布生成的随机变量，它们加在一起的总效应，是符合正态分布的。对于平稳的随机过程而言，其分布也是趋于正态的。
决定正态分布的两个参数：平均值 u 基本为零（不为零时，直流分量也很容易处理），唯一能表征随机信号的就剩均方值（ u=0 时等于方差）σ^2 ，也就是平均功率了。再具体一点，对于平稳随机信号而言，描述 x(t) 是没有意义的，描述平均功率才有意义。
如何才能描述平均功率呢？
帕斯瓦定理：那就是信号的能量（或者平均功率）无论在时域看，还是在频域看，都是一样的。
平稳随机信号 x(t)的幅值是呈现正太分布的，其平均值接近为零（或去除直流分量后），均方值或方差（也就是平均功率）是固定的，既然平均功率（或能量）在时域和频域是守恒的，而在时域 x(t) 是随机的，不可描述，那我们可以换到频域去啊：
其中：
，表示了信号的平均功率（或能量）在频域上的分布，即单位频带的功率随频率变化的情况，故称之为信号的自功率谱密度函数，简称自功率谱或自谱。
与 f 轴包围的面积等于信号 X(t)的平均功率，即 X(t) 的幅值分布的方差或均方值。同时可以看出，当 X(t) 表示加速度时（单位为 g），
的单位就变成了 g^2/Hz.
自相关又是什么概念？
简单理解：就是一个信号在不同时间段的区别。
对于随机信号：时间趋于无穷大时，自相关趋于 0，当时间趋于 0 时，自相关最大，等于平均值，也就是平均功率；
对于周期信号：自相关函数可以把随机信号中的周期成份检测出来，这是因为任何周期信号在所有的时移上都有一定形状的自相关函数图形。简单点来说：自相关函数能够检测出信号内部蕴藏的周期组分，而过滤掉了周期组分的相位信息。
明确以上背景后，那麽自相关函数和频域分析有什么关系？
前面我们分析了，信号的功率在时域和频域都是满足守恒定律的。而功率被定义成幅值的平方的时间平均分量，而这个过程，也可以看成是去除频域谐波分量的相位信息的过程，因为本质来说，一个简谐信号的相位是不影响其功率的。而自相关函数，也具有去除信号相位的功能，那自相关函数和功率密度谱是不是有什么深刻的联系呢？答案是肯定的，那就是维纳-辛钦定理（Wiener–Khinchin theorem），这个定理表明：信号的自相关函数与功率密度谱是一对傅里叶变换对。
也就是说：一个信号的功率密度谱，就是其自相关函数的傅里叶变换。
说到这里可以大致做个总结了：对于一个随机信号而言，时域信息是杂乱无章的，唯一的确定性信息但是在统计意义下得到的，即幅值呈正太分布，均方值也就是平均功率是固定的。根据帕斯瓦定理，信号的平均功率在时域和频域是守恒的，按道理说直接对时域信号进行傅里叶变换再取平方就可以。但不幸的事，随机信号的不满足傅里叶变换绝对值可积的条件，严格意义傅里叶变换不存在，于是发明了自相关函数的概念，将信号的蕴含的周期信号识别出来，并将相位信息去掉（相位不影响平均功率），于是就出现了最终形式维纳-辛钦定理：一个信号的功率密度谱，就是其自相关函数的傅里叶变换。提炼一下就是：随机信号→幅值正太分布→均方值（平均功率）→帕斯瓦定理（功率守恒）→自相关函数（去除相位信息）→维纳-辛钦定理（最终形式）。
三：夹具验收的一般要求
前面我们系统的介绍了有关共振相关的概念，那么这些参数概念怎么运用到我们的实际工作—夹具验收当中呢？下面我们就一起来看下。
夹具的主要功能需求如下：
1. 满足试件的固定安装；
2. 保证振动试验的目标能量既无损失也无额外增加的传递到试件上去；
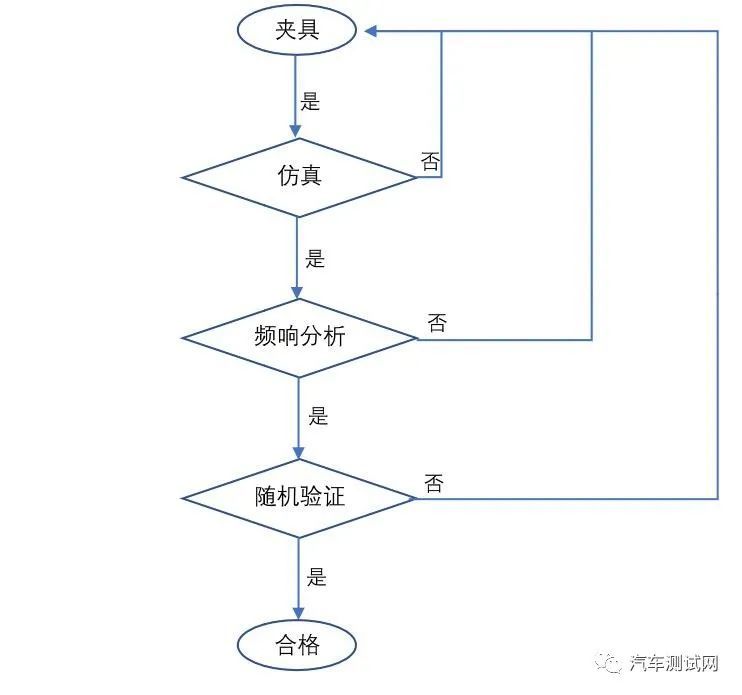
对于第一点通过机械结构设计很容易实现，但是对于第二点在实际应用中需要通过哪些方法去评估呢？参考下面流程可作为评估夹具的基本方式：
一．仿真：通过对夹具的数模进行有限元分析，可以初步看出夹具设计的薄弱环节。
仿真要实现的目标：
1. 得出夹具的不同阶的固有频率，通过不断优化结构，以尽可能达到一阶固有频率在工作频率范围之外；
2. 模拟出夹具不同的结构处的位移量大小，进行结构优化加强；
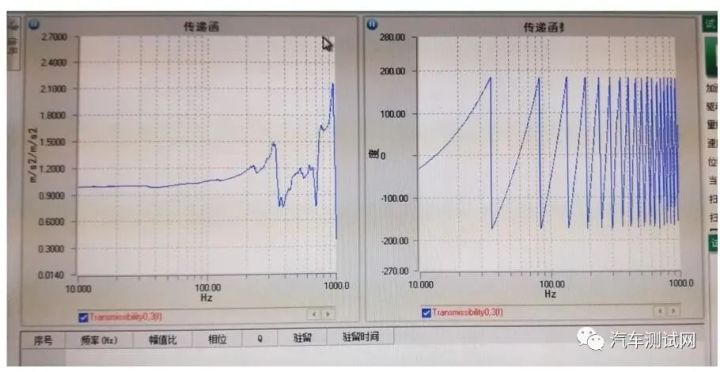
二．频响分析：通过模态实际振动分析，对夹具的实际频响特性进行分析，以定性分析夹具的共振影响水平。实际做法是：用定加速度的正弦振动去激励夹具，得出夹具的频响结果。
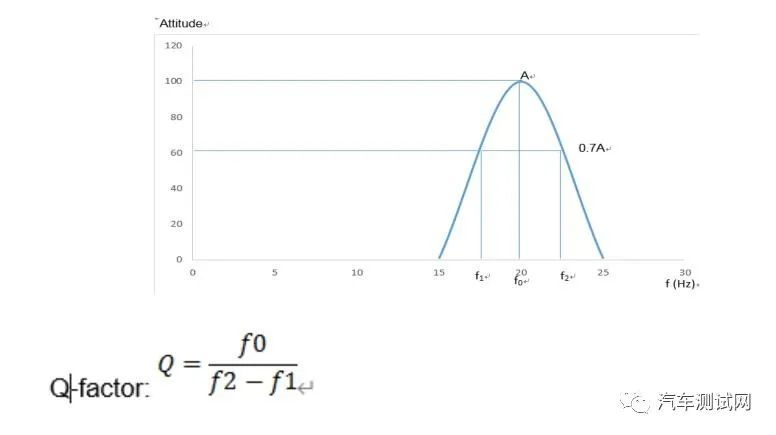
1. 通过结果：可以得出夹具频响的幅值比，相位变化，品质因数，共振频率等关键参数。他们之间的关系阐述如下：
2. 一般判定存在共振的条件是：幅值比大于 2，相位变化在不大于π/2。这两个条件满足，基本判定该频率点即为共振频率点。
3. 满足共振频率点的条件后，还要通过品质因数来判定该共振响应会产生多大影响。下面这个表格是摘自《环境与试验技术》一书中关于夹具验收标准的一般推荐参考：
半功率带宽：以上表格中的 Q 值(品质因数)和 3dB 带宽的数学关系如下：
【振动程序中频响函数】
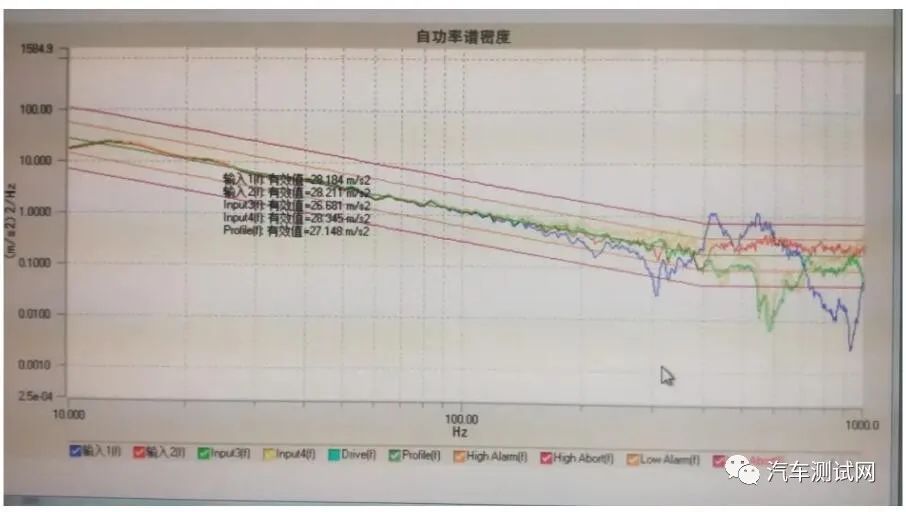
三．随机振动验证：当前各大主机厂的试验标准中关于振动要求，对于内饰件来说基本都是随机振动。夹具完成以上两个环节的定性分析后，可以再按照标准要求的随机振动的参数对夹具进行试振，监控每个样件固定点位置的响应频谱曲线，得出等效加速度值是否满足要求。
GMW3172 标准中对随机监控响应有明确的 tolerance 要求，即
1. 各个点监控的等效加速度值满足在+/- 20%的范围内；
2. 各个振动交越频率点的功率谱密度满足在+/- 20%的范围内。
【GWM3172 标准夹具判定描述】
【随机监控谱图：等效加速度】
值得注意的是：GMW3172 标准中 2015 版本后，将频响特性——共振扫寻的要求给remove 掉了，只对夹具实际的随机振动响应提出了明确的要求。笔者理解这样做的目的可能是因为对于夹具共振的验收标准，目前国内国际都没有明确统一的标准要求！夹具的重量不同、产品不同、结构不同其要求都是不一样的。这就需要产品的设计者结合设计的产品、实际的夹具定性定量分析的结果自行评估夹具的可接受性。
来源：汽车测试网，作者：王杰
投稿邮箱：marketing@auto-testing.net
- 下一篇：电驱动两挡箱的技术应用情况
- 上一篇：测量振动 | 解密关于振动测量的基本概念
广告
广告
编辑推荐
最新资讯
-
氢燃料电池卡车创企“冰河时代”！HVS命悬
2024-11-17 09:45
-
小米端到端大模型：智能驾驶的“新大脑”
2024-11-17 09:44
-
阿斯顿马丁推出新款 F1 模拟器
2024-11-17 09:43
-
汽车动力电池系统试验综述
2024-11-16 08:25
-
汽车可靠性前沿技术研讨会在重庆成功召开
2024-11-16 07:33
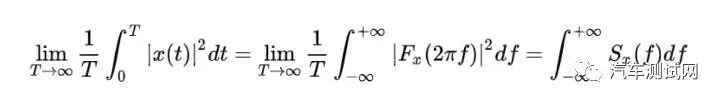
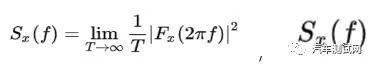
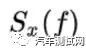
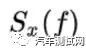
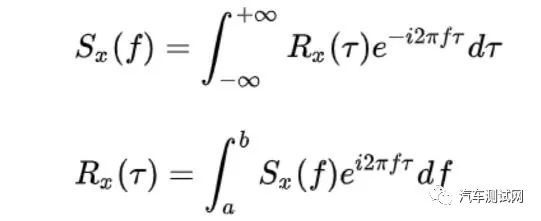
广告
广告
