广告
无人驾驶控制算法之MPC控制
2021-12-22 22:10:20· 来源：智能运载装备研究所
模型预测控制（MPC）可在考虑控制约束、非线性等前提下实现系统性能的最优控制，因而是无人驾驶车辆动力学控制算法中应用较多也是最重要的一种方法。因此，本文
模型预测控制（MPC）可在考虑控制约束、非线性等前提下实现系统性能的最优控制，因而是无人驾驶车辆动力学控制算法中应用较多也是最重要的一种方法。因此，本文就针对MPC的工作原理、算法结构开展讨论，介绍了MPC与LQR、PID的优缺点，最后基于无人驾驶车辆运动学模型设计了MPC控制器，然后将线性化的MPC问题转化为标准二次规划问题，最后，在文章的末尾还给出了相关的仿真代码供大家交流讨论。
一.MPC简介
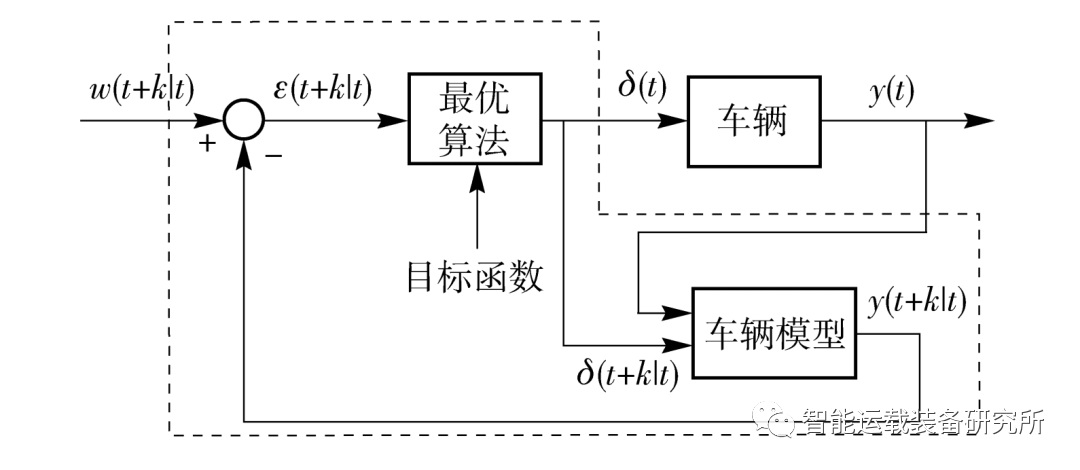
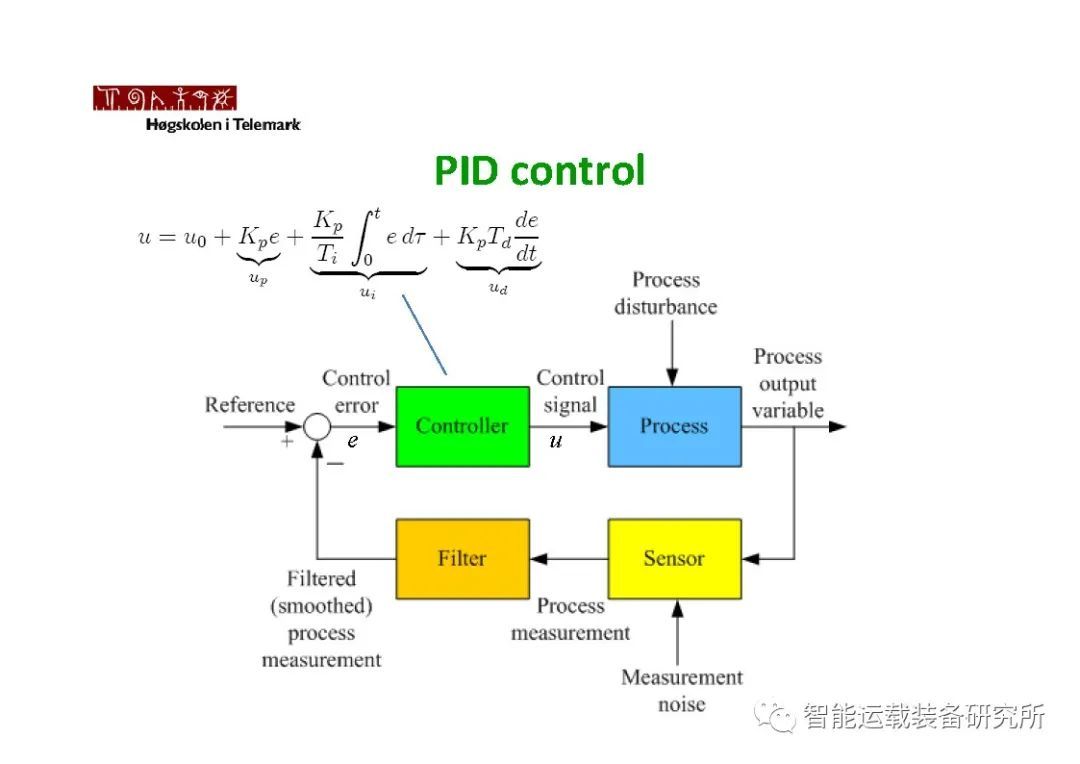
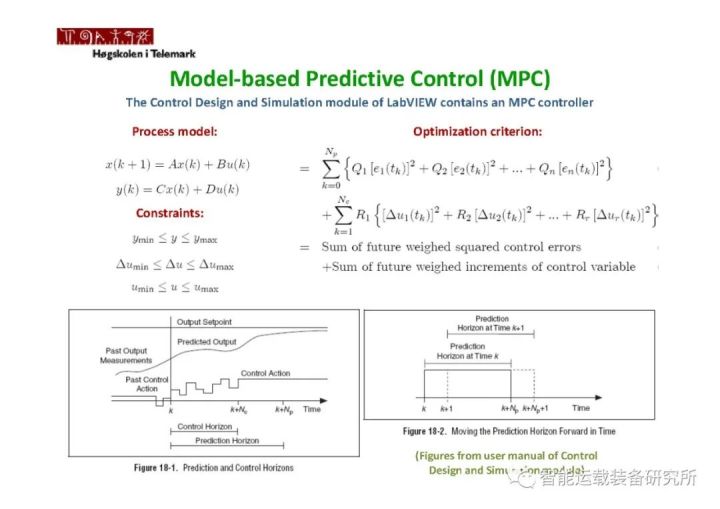
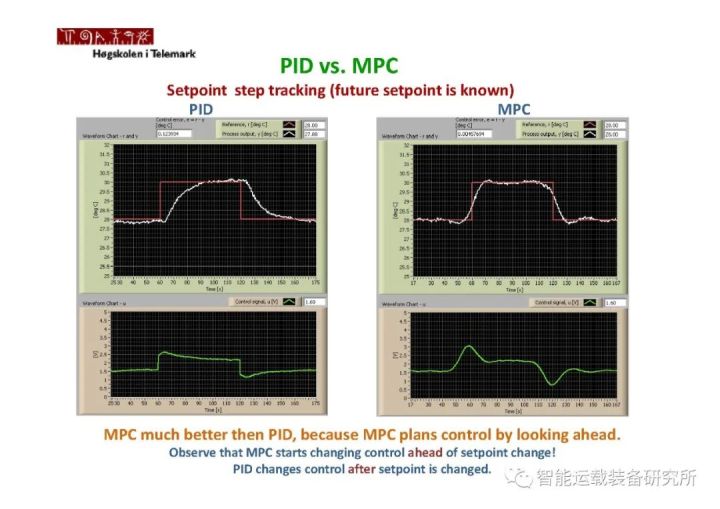
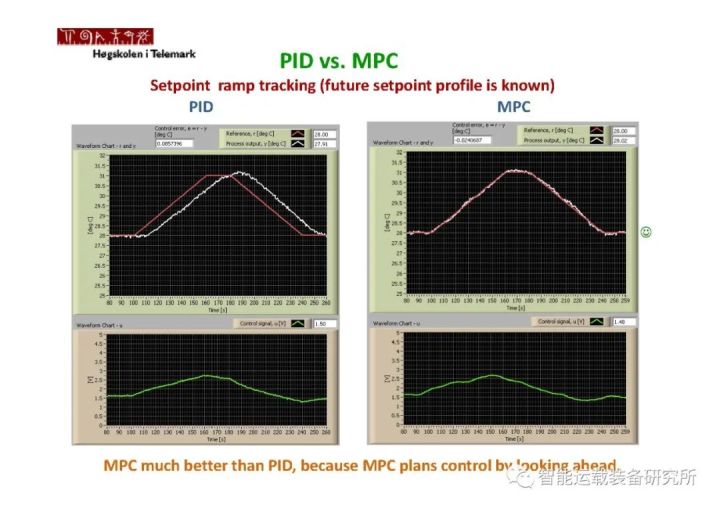
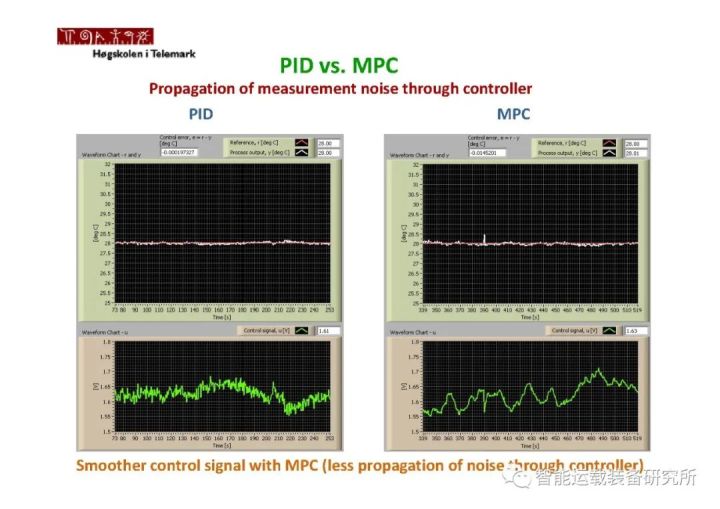
如下图所示，MPC是一种多变量控制策略，其中涉及了：参考轨迹，过程内部动态模型即车辆模型，控制量的历史数值，在预测区间上的一个代价函数方程J。最优控制量可由以上各量求出。MPC最大的特点在于，相对于LQR控制而言，MPC可以考虑状态变量、输出变量和控制变量的各种复杂约束，而LQR、PID等控制只能够考虑输入输出变量的各种约束，甚至难以求解考虑约束的优化问题。MPC可应用于各类线性和非线性系统。有关PID相关理论可阅读公众号文章：无人驾驶控制算法之PID控制、PID控制原理及参数调节，有关LQR相关理论可阅读公众号文章：无人驾驶控制算法之LQR控制。
二.作用原理
MPC在每个采样时刻，根据获得的当前测量信息，在线求解一个有限时间带约束的最优化问题，并将得到的控制序列的第一个元素作用于被控系统。在下ー个采样时刻，重复上述过程：用新的测量值作为此时预测系统未来动态的初始条件，迭代更新优化问题并重新求解。如需详细了解MPC的作用原理，可观看如下视频内容帮助理解MPC。
已关注
关注
重播 分享 赞
智能运载装备研究所
已同步到看一看写下你的想法
0 / 0
00:00 / 04:55
转载
,
无人驾驶控制算法之MPC控制
智能运载装备研究所
已同步到看一看写下你的想法
进度条，百分之0
播放
00:00
/
04:55
04:55
全屏
倍速播放中
0.5倍
0.75倍
1.0倍
1.5倍
2.0倍
超清
高清
流畅
您的浏览器不支持 video 标签
继续观看
无人驾驶控制算法之MPC控制
视频详情
综上，MPC算法包括三个步骤：
（1）根据系统状态方程预测系统未来动态；
（2）求解带约束的优化问题；
（3）将最优解的第一个元素作用于被控系统。
这三步是在每个采样时刻重复迭代进行的，且无论采用什么样的模型，每个采样时刻得到的测量值都作为当前时刻预测系统未来动态的初始条件，在线求解优化问题获得优化序列是MPC和传统控制方法的主要区别，因为后者通常是离线求解一个反馈控制律，并将得到的反馈控制律一直作用于系统，而MPC是根据实际测量结果实时在线优化得到的最优反馈控制律，且考虑了系统的各类约束条件，所得的控制策略更合理。
在这里给出两点说明：
（1）MPC是反馈控制策略，每次求解优化问题后都将得到的控制序列中的第一个元素作用于被控对象，在下一个采样周期时的测量值又被使用上了，用下一时刻的测量值求解下一时刻的控制值。故这是一个在线实时反馈最优控制策略。
（2）当系统模型是线性时，MPC问题最后都可以转化为二次规划（QP）问题，转化成QP问题更便于实时求解，有关QP相关理论可参考公众号文章：无人驾驶控制算法之QP算法。
关于MPC的控制原理可参考下列幻灯片内容。
三.MPC结构
MPC主要包含三部分：模型预测、滚动优化和反馈校正。如需详细了解MPC的算法结构，可观看如下视频内容，视频里面详细讲解了MPC的算法逻辑与编程仿真。
已关注
关注
重播 分享 赞
智能运载装备研究所
已同步到看一看写下你的想法
0 / 0
00:00 / 16:09
转载
,
无人驾驶控制算法之MPC控制
智能运载装备研究所
已同步到看一看写下你的想法
进度条，百分之0
播放
00:00
/
16:09
16:09
全屏
倍速播放中
0.5倍
0.75倍
1.0倍
1.5倍
2.0倍
超清
高清
流畅
您的浏览器不支持 video 标签
继续观看
无人驾驶控制算法之MPC控制
视频详情
1.模型预测
在MPC算法中，需要一个描述对象动态行为的模型，这个模型的作用是预测系统未来的动态，即能够根据系统k时刻的状态和k时刻的控制输入，预测到k+1时刻的输出。在这里k时刻的输入正是用来控制系统k+1时间的输出，使其最大限度的接近k+1时刻的期望值。故我们强调的是该模型的预测作用，而不是模型的形式。
2.滚动优化
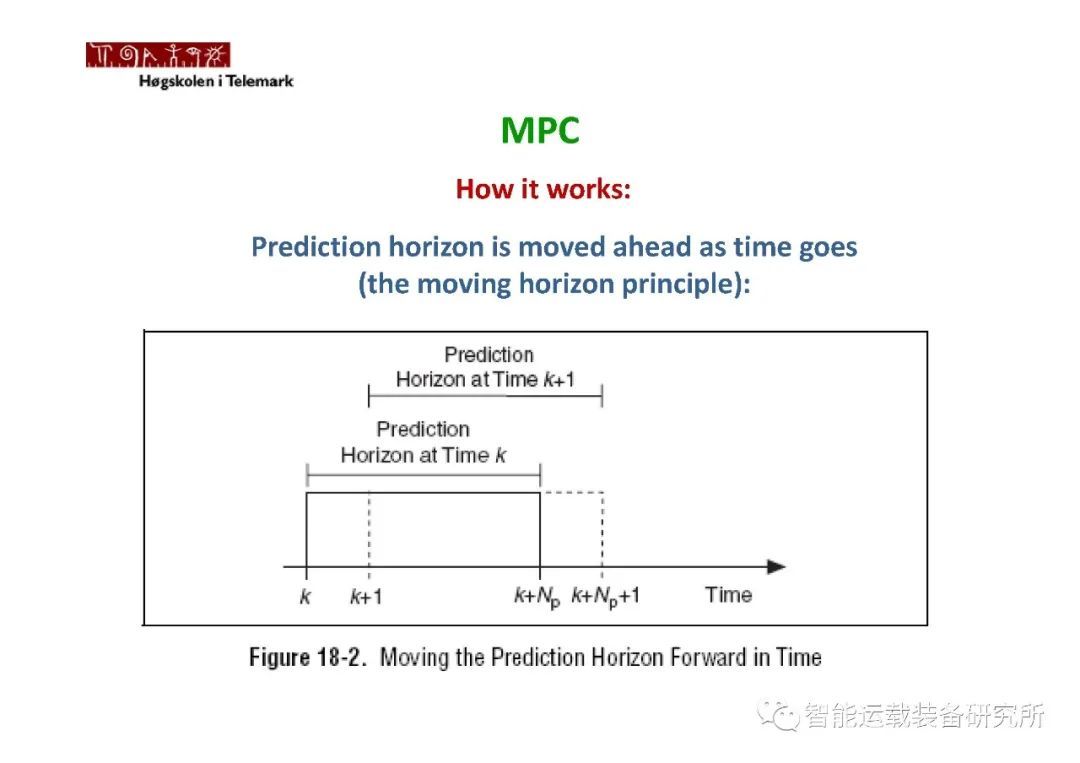
因为外部干扰和模型失配的影响，系统的预测输出和实际输出存在着偏差，如果测量值能測到这个偏差，那么在下一时刻能根据这个测量到偏差的测量值在线求解下一时刻的控制输入，即优化掉了这个偏差值。若将求解的控制输出的全部序列作用于系统，那么k+1时刻的测量值不能影响控制动作，也就是说测量值所包括的外部干抗或模型误差信息得不到有效利用。故我们将每个采样时刻的优化解的第一个分量作用于系统，在下ー个采用时刻，根据新得到的测量值为初始条件重新预测系统的未来输出并求解优化解，继续讲这个时刻的优化解的第个分量作用于系统,这样重复至无穷。故预测控制不是采用一个不变的全局优化目标，而是采用时间向前滚动式的有限时域优化策略。这也就是意味着优化过程不是一次离线进行，而是反复在线进行的。
3.反馈校正
到下一个采样时间点根据新的状态重新进行模型预测和滚动优化。
四.无人驾驶控制算法仿真实例分析
1.车辆运动学建模
无人驾驶车辆运动规划与控制需要通过对车辆运动学或者动力学系统的控制来实现。建立合理的车辆系统模型不仅是设计MPC的前提，也是实现车辆道路跟踪功能的基础。因此，在建立MPC时，必须根据无人驾驶车辆的具体行驶工况，通过选取合适的控制变量，建立能够准确描述无人驾驶车辆运动关系约束的运动学模型。实际上，车辆在地面运动的动力学过程是非常复杂的，为了尽量描述车辆运动，需要建立复杂的微分方程组，并用多个状态变量来描述其运动。用于MPC的模型只要能够表现出车辆运动学与动力学约束，就可以使MPC实现轨迹跟踪控制目的。因此，首先通过建立能够尽量准确反映车辆运动特性，并且有利于MPC设计的简化车辆运动学模型。
车辆运动学模型如下图所示，在惯性坐标系OXY下，(
- 下一篇：发动机主动控制原理与应用
- 上一篇：纬湃科技-48V高功率电驱动系统的设计与开发
广告 
广告
编辑推荐
最新资讯
-
车载通信框架 --- 智能汽车车载通信架构浅
2024-12-23 08:40
-
全国首例！武汉车网智联公司完成智能网联测
2024-12-23 08:39
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
-
车载无线广播收音机还需要吗？
2024-12-23 07:37
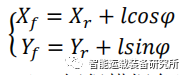
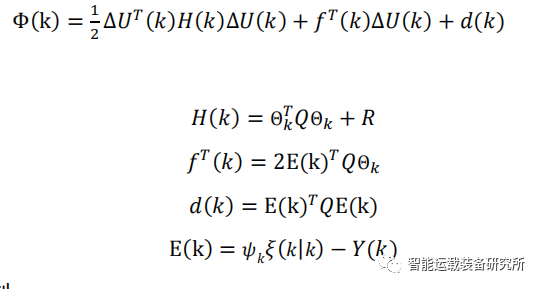
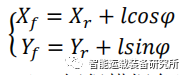
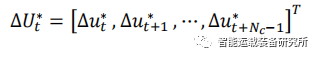
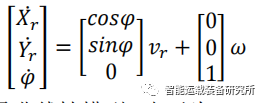
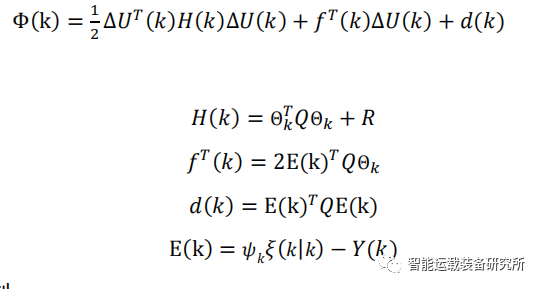
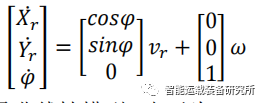
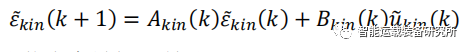
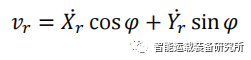
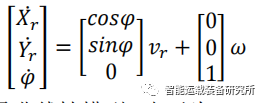
广告
广告
