连续系统与离散系统LQR问题求解:以车辆二自由度模型为例

















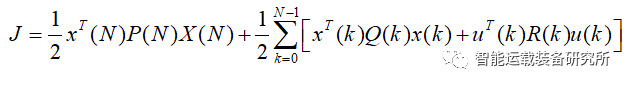
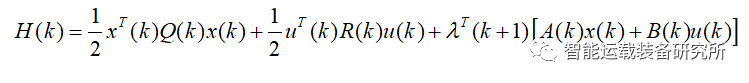




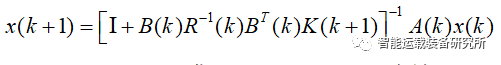










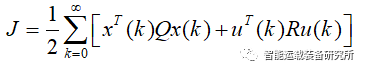



编辑推荐
最新资讯
-
大卓智能端到端直播实测,16公里复杂路段挑
2025-04-25 17:16
-
《汽车轮胎耐撞击性能试验方法-车辆法》等
2025-04-25 11:45
-
“真实”而精确的能量流测试:电动汽车能效
2025-04-25 11:44
-
GRAS助力中国高校科研升级
2025-04-25 10:25
-
梅赛德斯-AMG使用VI-CarRealTime开发其控制
2025-04-25 10:21





 广告
广告





























































