广告
几种常见的路径跟踪算法
2022-01-03 17:25:28· 来源：智能运载装备研究所 作者：杜二磊
一.路径跟踪简介在路径跟踪过程中，参考轨迹曲线与时间参数无关，跟踪轨迹时可以假设无人车以当前速度匀速行驶，以一定的代价规则形成行驶路径趋近于参考路径；
一.路径跟踪简介
在路径跟踪过程中，参考轨迹曲线与时间参数无关，跟踪轨迹时可以假设无人车以当前速度匀速行驶，以一定的代价规则形成行驶路径趋近于参考路径；而轨迹跟踪，其参考路径曲线与时间和空间均相关，并且要求无人车在规定时间内达到某一预设好的参考路径点。
图1 智能车路径跟踪问题
路径跟踪一般是通过控制转向角度，实时对预测轨迹的跟踪。不仅仅要求跟踪效果的准确性，从而保证智能车的行驶安全，还要求跟踪过程中车辆的稳定性和安全性。现有路径跟踪控制方法包括：
（1）基于道路几何原理的路径跟踪控制，如纯跟踪控制、Stanley控制等；
（2）基于经典控制理论路径跟踪控制，如PID控制、线性反馈控制等；
（3）基于现代控制理论路径跟踪控制，如模型预测控制、最优控制等。
本文在分析现有路径跟踪控制方法的基础之上，选择基于经典控制理论的PID控制、基于道路几何的Stanley控制以及基于现代控制理论的最优控制三种方法完成智能车路径跟踪控制器设计。并针对设计的控制算法进行仿真分析，对比三种控制算法的优缺点，为路径跟踪控制进一步研究提供一定的参考与借鉴意义。
二.基于PID控制算法的路径跟踪
1.PID算法简介
首先进行期望值输入，然后和实际值进行偏差计算。所得到的偏差的比例kp、ki、kd的线性组合构成控制量，在传递给被控对象，被控对象输出实际值，详细可参考公众号文章：无人驾驶控制算法之PID控制和PID控制原理及参数调节。
图2 PID算法原理
PID控制器为：
其中，u(t)为控制器控制量，Kp为控制器比例项系数，Kd为控制器微分项系数，Ki为控制器积分项系数，e(t)代表期望值与实际值之间的偏差。
2.车辆-道路相对位置关系
假设车辆预瞄前方道路上一点A，它在惯性坐标系下的坐标为，到点A参考路径曲线的切线方向与车辆坐标系x轴夹角为，车辆质心位置为，车辆坐标系x轴线与X轴夹角为，如图所示。
图3 车辆道路相对位置关系
在车辆坐标系xoy下，可得到点A与车辆质心的位置偏差及方向偏差，其相对位置几何关系有：
其中上式中le为预瞄距离；de为车辆坐标系下xoy车辆质心与预瞄点A的横向距离偏差；φe为车辆坐标系xoy下车辆质心与预瞄点A的航向偏差。
利用PID，车辆路径跟踪转向过程中可通过计算横向距离偏差与航向偏差从而得到前轮转角：
上式Kpde、Kdde、Kide代表横向偏差的比例、微分和积分因子；Kpφe、Kdφe、Kiφe代表航向偏差的比例、微分和积分因子；de表示车辆质心与参考点之间的横向偏差；φe为航向偏差。
三.基于Stanley控制算法路径跟踪
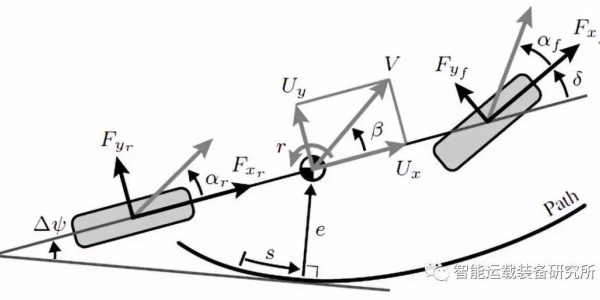
Stanley控制算法是一种基于横向偏差的非线性反馈函数，并且能实现横向偏差指数收敛于0。如图4所示，横向偏差de是车辆前轮到给定最近轨迹点p的距离；δe是给定轨迹上切线方向与车身航向之间的夹角；φe是前轮线速度与车身航向之间的夹角。
图4 Stanley控制算法示意图
在不考虑横向误差的情况之下，需要车辆跟随期望轨迹运动，需要前轮转角时刻保持与期望轨迹上点的切线方向一致，即前轮转角为φe。
在不考虑航向误差的情况之下，需要车辆跟随期望轨迹运动，则前轮转角需要消除横向偏差，即前轮转角为δe。
因此同时考虑横向偏差和航向偏差，前轮转角为：
根据Stanley示意图可得：
其中，
所以，
当横向偏差很小时，
趋近于0。则
由k>0可见，横向偏差de指数收敛于0，收敛速度取决于参数k。因此，
则前轮转角为
四.基于LQR控制算法的路径跟踪
1.车辆运动学模型
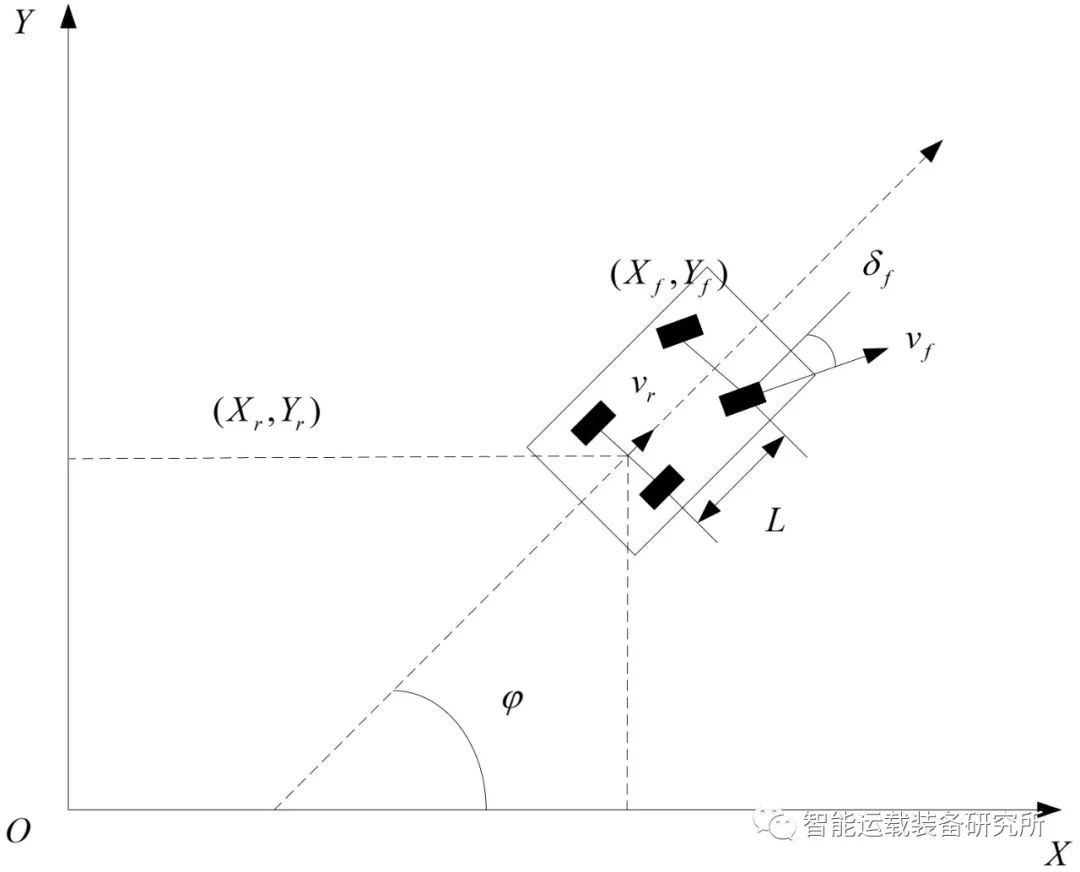
车辆运动学模型如图5所示。在惯性坐标系XOY下，(Xf,Yf)和(Xr,Yr)分别是车辆前轴和后轴的轴心坐标，φ为车辆的横摆角，δf为前轮转角，vr为车辆的后轴中心速度，L为汽车轴距。
图5 车辆运动学模型
车辆运动学模型为
2.运动学状态空间模型
根据车辆运动学方程，将车辆运动状态系统看作一个输入u=[v,δ]^T以及状态参数X=[x,y,φ]^T的控制系统。可表示为：
在车辆控制系统中，期望轨迹可表示为：
上式中
将车辆运动学非线性模型在期望点(Xc,uc)处进行泰勒式展开，忽略高阶项，可得：
记
可得：
即
可得线性化之后的路径跟踪误差模型，将其离散化可得：
其中，T=0.01s为采样时间，系统矩阵为
3.LQR控制器设计
LQR推导过程本文不做详细赘述，具体可参考公众号文章：无人驾驶控制算法之LQR控制和连续系统与离散系统LQR问题求解：以车辆二自由度模型为例。在建立车辆运动学模型之后，可得车辆的运动状态空间方程，给定权重矩阵Q和R后进而可以求得其LQR控制器。
五.对比分析
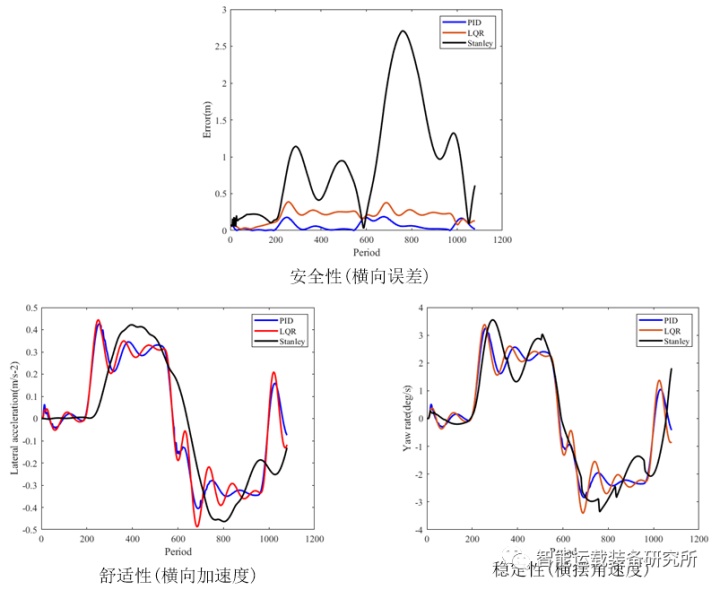
从安全性、舒适性、稳定性三个方面来评价PID、Stanley、LQR三种控制算法，验证三种控制方法的有效性及优缺点。
图6 三种控制算法效果对比图
评价结果如下表1所示。可见，基于线性化运动学模型的LQR所得结果综合性能优于其他两种方法。
表1 三种控制算法评价结果
广告
最新资讯
-
E-NCAP将发布全球首个重卡安全评级计划
2024-04-25 17:26
-
中国保险汽车安全指数新能源汽车测评规程框
2024-04-25 16:44
-
地平线发布征程6和高阶城区智驾样板间，以
2024-04-25 09:58
-
充电桩GB/T-2023设计要点
2024-04-25 09:49
-
中国汽车工程学会汽车大数据应用分会筹备会
2024-04-25 09:46
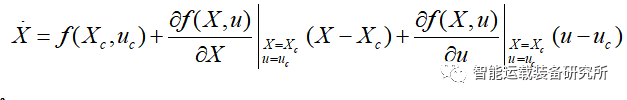
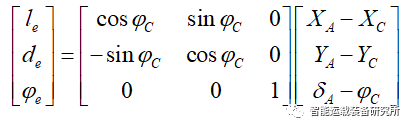
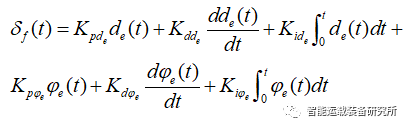
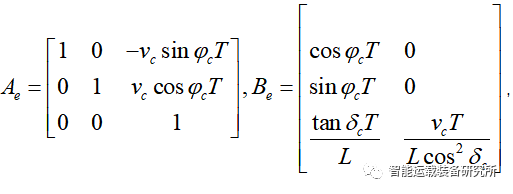
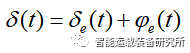
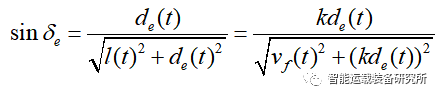
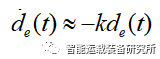
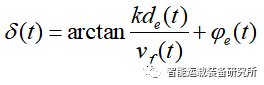
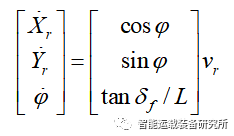
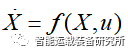
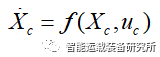
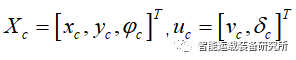
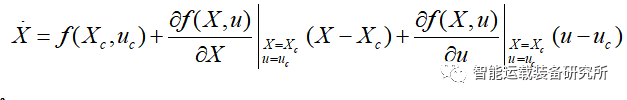
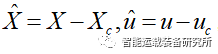
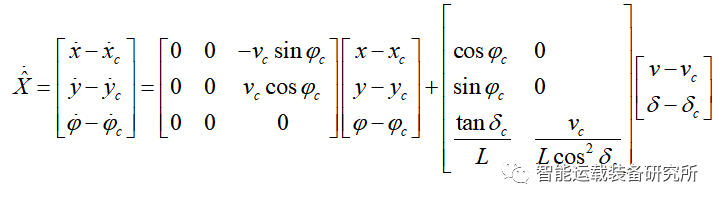
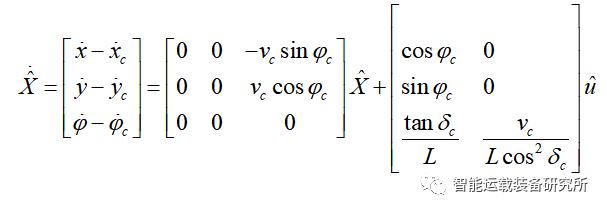
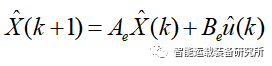
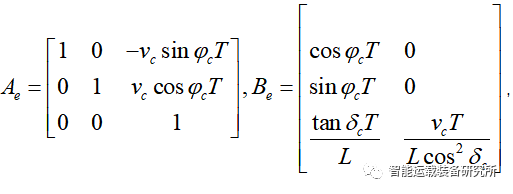
广告
广告
