寻找供应商
广告
首页 > 汽车技术 > 正文

基于MPC的设施保持系统设计

2022-01-08 11:45:13·  来源：智能运载装备研究所  作者：杜志彬  
　
一、车辆动力学模型不同程度保持（LKA）算法将车辆的横向动力进行解耦，在考虑横向周期时，确定模型的速度为常态，并基于模型自由度进行建模，在如下情况中控制
一、车辆动力学模型
不同程度保持（LKA）算法将车辆的横向动力进行解耦，在考虑横向周期时，确定模型的速度为常态，并基于模型自由度进行建模， 在如下情况中控制的应用，则车辆所呈现的状态方程：




设置期望的横摆角速度为rdes，构造增广系统




为最后的 LKA 功能，利用其车载检测检测线信息，假设输出 1 和 E2 分别为车辆检测与设备中心线的偏差及侧面检测模型，则传感器检测模型


其中，rho为曲率半径。将其写入成状态空间模型





将系统增广可得新的状态空间模型





MPC是一种离散量算法，因此，首先需要将其离散化，化验可参考公众号：文章二自由度动力学模型模型及其离散化应用，离散化后的系统为：



其中，Ak=A3*T+I，Bk=B4*T，其中，T=0.1s为时间。
二.MPC控制器设计
模型预测控制（MPC）包括三大部分，分别是模型预测、滚动优化及反馈校正，关于MPC的详细知识可参考公众号文章：无人驾驶控制算法之MPC控制、基于二自由度模型的MPC在车辆横向控制中的应用、模型预测控制系统总结。首先建立性能指标函数：




考虑车辆的物理约束（硬约束），前轮转角被限制在[-0.5,0.5] rad/s。由上述可得最终的MPC问题模型如下所示：



为了求解上述MPC问题，构造增广的状态向量为



则得到一个增广的状态空间模型



其中，系统矩阵为



则模型预测结果为


新的状态空间方程的系统输出量如下：


为了使得上述关系表述的更加明确，将系统未来时刻的输出以矩阵的形式表达，具体如下：



其中，


在预测时域内的状态量和输出量都可以通过系统当前的状态量
和控制时域内的状态增量
计算得到，这也就是MPC中的预测功能的实现。
定义参考输出向量为


令
，将其代入性能指标函数，得：


其中最后三项为常数，在优化求解时可以忽略不计，则性能评价函数可以进一步表示为：



令



则性能指标函数可写成如下形式


至此，MPC问题转化为一个二次规划问题。进而可以使用Matlab中提供的QP问题求解器quadprog进行求解，从而得到在控制时域内的一系列控制输入增量，具体表示如下：



将QP求解的最优控制序列的第一个元素
作为实际的控制输入增量作用于线控转向系统，即


系统执行这一控制量直到下一时刻。在新的时刻，系统根据状态信息重新预测下一段时域的输出，通过优化过程得到一个新的控制增量序列。如此将预测域和控制域依次向下一个时刻进行滚动优化，如下图所示。



三.程序概述
%% Lane Keeping Assist System Using Model Predictive Control
% This example shows how to use the block in
% Simulink(R) and demonstrates the control objectives and constraints of
% this block.
% Add example file folder to MATLAB(R) path.
addpath(fullfile(matlabroot,'examples','mpc','main'));
%% Lane Keeping Assist System
% A vehicle (ego car) equipped with a lane-keeping assist (LKA) system has
% a sensor, such as camera, that measures the lateral deviation and
% relative yaw angle between the centerline of a lane and the ego car. The
% sensor also measures the current lane curvature and curvature derivative.
% Depending on the curve length that the sensor can view, the curvature in
% front of the ego car can be calculated from the current curvature and
% curvature derivative.
%带有LKA功能的车辆配备有传感器，如摄像头，用以测量本车与车道中心线的横向偏差及相
%对横摆角（偏航角）。该传感器还可测量当前位置的曲率及曲率的变化率。基于传感器可
%视的车道范围，位于本车前方的曲率可以通过当前位置的曲率及曲率变化率计算得到。
%%
% The LKA system keeps the ego car travelling along the centerline of the
% lanes on the road by adjusting the front steering angle of the ego car.
% The goal for lane keeping control is to drive both lateral deviation and
% relative yaw angle close to zero.
%通过调整本车的前轮转角，LKA系统可以让本车沿着车道中心线行驶。车道保持控制的目标
%是使得横向偏差及偏航角趋近于零。
%% Simulink Model for Ego Car
% The dynamics for ego car are modeled in Simulink. Open the Simulink model.
mdl = 'mpcLKAsystem';
open_system(mdl)
% Define the sample time, |Ts|, and simulation duration, |T|, in seconds.
Ts = 0.1;
T = 15;
% To describe the lateral vehicle dynamics, this example uses a _bicycle
% model_ with the following parameters:
%为了描述车辆的横向动力学特性，本算法使用了车辆的二自由度（单车）模型，具体参数
%如下所示：
% * |m| is the total vehicle mass (kg)
% * |Iz| is the yaw moment of inertia of the vehicle (mNs^2).
% * |lf| is the longitudinal distance from the center of gravity to the
% front tires (m).
% * |lr| is the longitudinal distance from center of gravity to the rear
% tires (m).
% * |Cf| is the cornering stiffness of the front tires (N/rad).
% * |Cr| is the cornering stiffness of the rear tires (N/rad).
m = 1575;
Iz = 2875;
lf = 1.2;
lr = 1.6;
Cf = 19000;
Cr = 33000;
% You can represent the lateral vehicle dynamics using a linear
% time-invariant (LTI) system with the following state, input, and output
% variables. The initial conditions for the state variables are assumed to
% be zero.
%车辆的横向动力学特性可以使用LTI系统来表示，系统的状态、输入及输出变量在上面有
%具体说明。状态变量的初始条件假定为零。
% * State variables: Lateral velocity $V_y$ and yaw angle rate $r$
% * Input variable: Front steering angle $\delta$
% * Output variables: Same as state variables
%%
%状态变量：横向速度Vy、横摆角速度r
%输入变量：前轮转角δ
%输出变量：横向速度Vy、横摆角速度r
% In this example, the longitudinal vehicle dynamics are separated from the
% lateral vehicle dynamics. Therefore, the longitudinal velocity is assumed
% to be constant. In practice, the longitudinal velocity can vary and the
% Lane Keeping Assist System Block uses adaptive MPC to adjust the model of
% the lateral dynamics accordingly.
%在本算法中，将车辆纵向动力学与横向动力学解耦。因此，纵向车速假定为常数。实际上
%来说，车辆的纵向速度是可以变化的，LKA系统模块将使用自适应模型预测控制来相应得调
%整车辆的横向动力学模型。
% Specify the longitudinal velocity in m/s.
Vx = 15;
%确定纵向车速的：Vx = 15m/s
% Specify a state-space model, |G(s)|, of the lateral vehicle dynamics.
A = [-(2*Cf+2*Cr)/m/Vx, -Vx-(2*Cf*lf-2*Cr*lr)/m/Vx;...
-(2*Cf*lf-2*Cr*lr)/Iz/Vx, -(2*Cf*lf^2+2*Cr*lr^2)/Iz/Vx];
B = [2*Cf/m, 2*Cf*lf/Iz]';
C = eye(2);
G = ss(A,B,C,0);
%% Sensor Dynamics and Curvature Previewer
% In this example, the Sensor Dynamics block outputs the lateral deviation
% and relative yaw angle. The dynamics for relative yaw angle are
% $$\dot{e}_2 = r-V_x\rho$, where $\rho$ denotes the curvature. The
% dynamics for lateral deviation are $\dot{e}_1 = V_x e_2+V_y$.
%传感器动力学及曲率预瞄
%在本算法中，传感器动力学模块输出横向偏差e1及角度偏差（偏航角）e2。
%rho为曲率半径。其中e1和e2满足动力学方程




% The Curvature Previewer block outputs the previewed curvature with a
% look-ahead time one second. Therefore, given a sample time $Ts = 0.1$,
% the prediction horizon |10| steps. The curvature used in this example is
% calculated based on trajectories for a double lane change maneuver.
%曲率预瞄模块输出前视时间为1s的预测曲率。因此，给定的采样时间为Ts=0.1，
%预测域为10步。本算法所使用的曲率是基于双移线工况的轨迹计算所得。
% Specify the prediction horizon and obtain the previewed curvature.
PredictionHorizon = 10;
time = 0:0.1:15;
md = getCurvature(Vx,time);
%% Configuration of the Lane Keeping Assist System Block
% The LKA system is modeled in Simulink using the Lane Keeping Assist
% System block. The inputs to the LKA system block are:
% * Previewed curvature (from lane detections)
% * Ego longitudinal velocity
% * Lateral deviation (from lane detections)
% * Relative yaw angle (from lane detections)
%the Lane Keeping Assist System模块的结构
%LKA系统在simulink中的建模是使用了the Lane Keeping Assist System block。该模块的
%输入如下：
%预瞄曲率、本车纵向速度、横向偏差及相对横摆角（偏航角）
% The output of the LKA system is the front steering angle of the ego car.
% Considering the physical limitations of the ego car, the steering angle
% is constrained to the range [-0.5,0.5] rad/s.
u_min = -0.5;
u_max = 0.5;
%该LKA系统的输出是本车的前轮转角。考虑到本车的物理约束（硬约束），前轮转角被限制
%在[-0.5,0.5] rad/s。
% 对于这个例子，车道保持辅助的默认参数
% 系统块匹配仿真参数。如果你的模拟
% 参数与默认值不同，然后更新块
% 参数。
%对于本算法， 车道保持辅助系统模块的默认参数即为仿真参数。如果你的
%仿真参数与默认值参数，因此请相应地对相关进行更新。
%% 模拟分析
% 运行模型。
模拟（MDL）
% 绘制模拟结果。
mpcLKAplot（注销）
% 横向偏差和相对偏航角都收敛到零。
% 即ego汽车根据预览图紧跟道路
% 曲率。
% 从 MATLAB 路径中删除示例文件夹，并关闭 Simulink 模型。
rmpath(fullfile(matlabroot, 'examples' , 'mpc' , 'main' ));
bdclose(mdl) 
分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• L2和L3级智能驾驶车辆驾驶员的角色转变研究 • 产业专利分析—智能座舱之人机交互技术
• 区域化配电的技术及趋势 • 汽车制动踏板感匹配方法探讨
• 电动汽车动力电池碰撞安全性及建模仿真 • 欧盟2023年温室气体排放下降8.3%，交通运输脱碳需奋起直追
• 详解！续航2900公里的康明斯燃料电池卡车-H2Rescue • 电动汽车轮胎的特点和创新要突出的技术亮点
• 大众PEP开发流程详解 • 一文讲清全球定位系统GPS
0 条相关评论
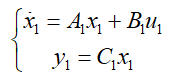
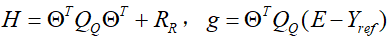
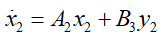
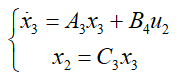
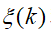
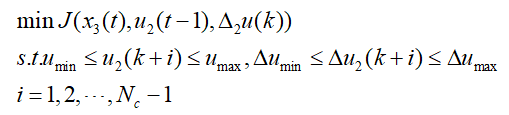
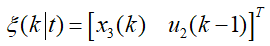
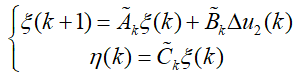
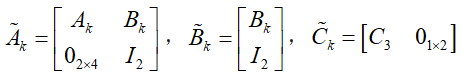
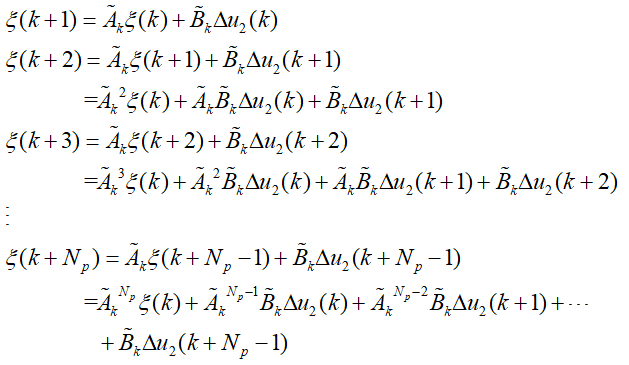
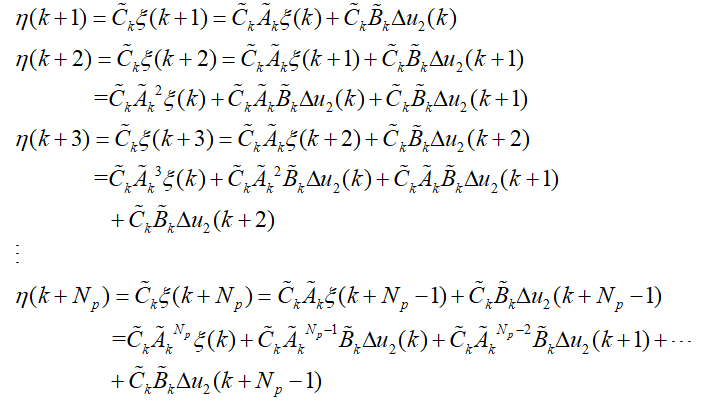
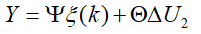
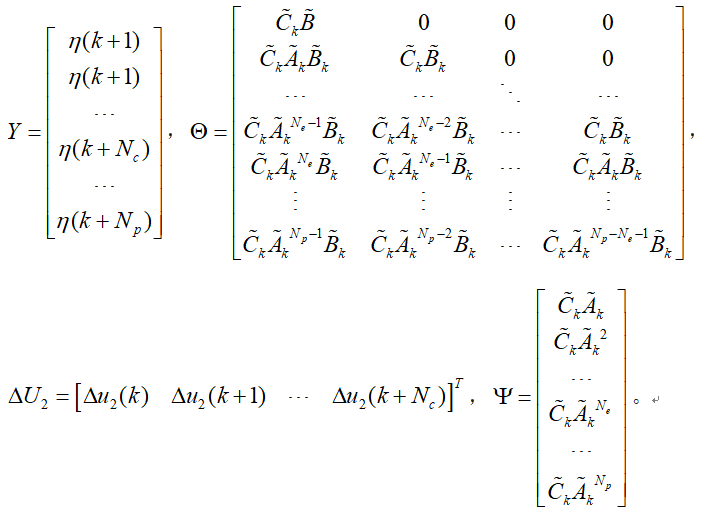
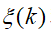
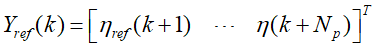
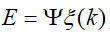
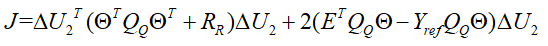
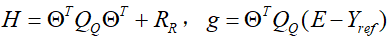
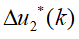
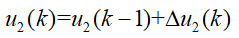
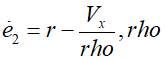
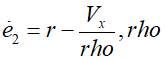
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25