广告
汽车可靠性试验中的置信度概念
2022-01-09 21:15:40· 来源：模态空间 作者：王朋波
01、概述在汽车开发过程中，需要进行整车及部件的可靠性试验。所谓可靠性，指的是零件或系统在在规定条件下和规定时间内，完成（或保持）规定功能的能力。可靠性
01、概述
在汽车开发过程中，需要进行整车及部件的可靠性试验。所谓可靠性，指的是零件或系统在在规定条件下和规定时间内，完成（或保持）规定功能的能力。
可靠性试验中经常遇到的一个问题是，如何在样本容量和试验时间（试验成本）之间进行平衡。即便是同种零件，它们之间仍然不会完全一致。我们无法对所有的零件都进行试验，只能从总体中抽取出一定容量的样本进行测试。为了从有限容量样本的信息中提取出总体参数，需要使用统计学领域的一些理论。
利用统计学方法进行总体估计通常有两种方法。一种叫做点估计，即使用单个数值来表示总体参数的估计值。另一种叫做区间估计，即利用样本数据来确定总体参数的一个估值区间，这个区间叫做置信区间，置信区间包含总体参数真值的概率就叫做置信度。
汽车行业常用的可靠性指标有平均寿命、可靠度、故障率等等。平均寿命是最常见的指标，它是一种总体均值；故障率则是一种总体比例。我们也经常用可靠度的概念来量化零件或系统的可靠性，可靠度指的是零件或系统在规定条件下和规定时间里能完成规定功能的概率，一般用 来表示。可靠度 通常随时间递减，将时间 作为变量，则有可靠度函数 。
如果我们要根据样本的平均寿命和可靠度来估算总体的平均寿命和可靠度，就需要与置信度建立关联。
02、抽样分布与总体参数估计
我们通常关心的是总体参数，例如总体的均值、方差和比例等等。但是可靠性试验不可能覆盖所有的零件，只能从总体 个零件中抽取 个零件作为样本，利用样本提供的信息来推断总体特征。重复选取容量为 的样本时，由每一个样本算出的统计量数值的概率分布，称为样本统计量的抽样分布。
从均值为 μ 、方差为 σ 的正态或非正态总体中，抽取样本量为 的随机样本，当 充分大时（通常要求大于30），样本均值 的分布近似服从数学期望为 μ ，方差为 σ 的正态分布。这就是统计学中著名的中心极限定理，可表示为下式
μσ 需要注意的是，如果总体不是正态分布，当 为小样本时，样本均值并不服从正态分布。
在研究总体特征时，不仅有均值估计，也有比例估计，即用样本比例计算总体比例。所谓比例，指的是总体（或样本）具有某种属性的零件数目与总体（或样本）所有零件数目之比。可靠度指的是在规定条件下和规定时间里能够完成规定功能的零件在总体所有零件中的占比，所以可靠度实质也是一种比例。
样本比例所有可能取值的概率分布就叫做样本比例的抽样分布。当样本量足够大时（对于样本比例 ，当 大于5，即可认为样本量足够大），样本比例f的抽样分布可近似为正态分布。样本比例f的数学期望就等于总体比例 π ， 的方差为 σππ 。即
πππ
03、区间估计与置信度
我们用样本统计量去估算总体参数，例如用样本均值去估算总体均值，用样本比例去估算总体比例，用样本方差去估算总体方差，通常用样本统计量加减抽样误差来给出总体参数的一个估值范围，这就叫做总体参数的区间估计。
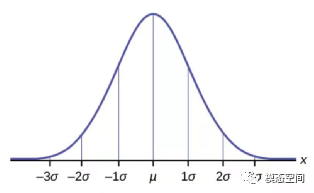
我们以总体均值的区间估计为例来讨论。对于样本量足够大的随机样本，样本均值 的数学期望为总体均值 μ ，样本均值的标准误差为 σσ ，服从正态分布，如图1。根据正态分布的基本特征可得出 落在 μ 两侧任何倍数标准误差范围内的概率。例如， 落在 μ 两侧各 σ 范围内的概率为95.45%。
图1 样本均值的正态分布
实际操作时情况恰好相反，我们知道 但不知道 μ 。好在 和 μ 的距离对称，如果 落在 μ 两侧各 σ 范围内，则 μ 也就落在 两侧各 σ 范围内。也就是说，用样本均值构造的两侧各 σ 的区间中（可以有无穷多个样本均值，构造出无穷多个区间），有95.45%的区间是包含总体均值的，其它区间不包含总体均值。
图2 总体均值区间估计示意
这样我们就得到了置信区间和置信度的定义：
-
由样本统计量所构造的总体参数的估计区间，称为置信区间，区间的最小值和最大值分别叫做置信下限和置信上限。
-
重复多次构造置信区间，置信区间中包含总体参数真值的次数所占的比率，称为置信度，也叫做置信水平。
-
置信水平一般用 来表示，其中 叫做显著性水平。例如置信水平为90%时，显著性水平 。
04、假设检验与显著水平
我们在进行可靠性试验时，不仅要对总体特征进行区间估计，有时还需要进行假设检验。所谓假设检验，就是首先提出一个对总体参数的假设，然后根据样本观察值对这个假设进行判断，决定是接受还是拒绝原假设。
例如某种零件的技术指标要求其平均寿命达到100小时（原假设）。我们随机抽取一批零件构造一个样本，寿命测试发现样本每个零件的寿命都不到10小时，与指标要求相距太远，就认为该种零件寿命未达到指标要求（即拒绝原假设）。
假设检验的基本思想是统计学的小概率反证法，即认为小概率事件在一次试验中不应当发生。因此首先假定原假设 成立，然后基于此假定来计算出现当前样本观察值的概率是多少。如果计算出的概率很小，就认为出现了小概率事件，因此拒绝原假设 。
在上面的关于零件平均寿命的例子中，我们拒绝了原假设。实际上也有存着这么一种可能：零件总体平均寿命已经达到100小时，只是我们凑巧选取了寿命最低的那一批零件作为样本，因此样本中各零件的寿命都不到10小时，导致我们做出了错误的判断。
我们是依据一个样本做出的判断，在 为真时，我们仍然可能做出拒绝 的判断，这叫做弃真错误。出现弃真错误的概率表示为
拒绝为真
我们无法完全排除弃真错误，但是我们会要求将犯错概率控制在一个很小的数值 之内，即
拒绝为真
上式中的 为显著性水平， 就是我们做出的拒绝 这个判断的置信度。
指定了显著性水平 ，就意味着出现弃真错误的概率最大为 ，这样我们可以计算出一个观察值（检验统计量）的取值区间，当观察值在这个区间内时，我们就拒绝原假设。这个取值区间叫做拒绝域。有关拒绝域的详细讲解可参考数理统计领域的资料，本文不再赘述。
我们不仅可以根据拒绝域进行决策，也可以利用 值进行决策。式(4)中的 值可以理解为当原假设正确时，得到所观测数据的概率。我们计算出 值，然后跟显著性水平 进行比较，当 ，即拒绝原假设 ，否则就不拒绝原假设 。
利用拒绝域进行决策，我们只是确认了犯弃真错误的概率小于 ，但并未确认犯错的概率究竟有多少，而 值则给出了我们犯错的实际概率。因此 值方法目前基本上取代了传统的拒绝域方法。
05、零件可靠度的二项检验法
我们在验证零件的可靠度时，就是利用 值进行决策。零件的可靠度检验经常采用二项检验法，每个零件只有“成功/失效”两种检验结果，零件达到了最低指标要求就是成功的，否则就是失效的。
如果零件的可靠度为 ，一共检验了 个零件。则指定的 个零件失效，其它 个零件成功的概率为 。考虑到这样的指定方式共有 种，则可知试验中出现 个零件失效的概率为
进一步可知试验中出现的零件失效数目 的概率为
我们设定一个假设 ：零件的可靠度 。我们认为在可靠度小于 的条件下，不应该只有 个零件失效，因此试图否定原假设 。
如果假设 为真，即零件的可靠度 ，则根据式（6）可知，零件失败数目 的概率即我们犯弃真错误的概率为
对于预先指定的显著性水平 或置信度 ，只要满足
则必然有 ，我们就可以拒绝原假设，即得出零件的可靠度 的结论。
对于没有发生失效 的特殊情况，式（8）变为
如果我们要验证置信度为 时某种零件是否具有R可靠性，可以根据式（9）计算无失效时的样本容量 。我们抽取了 个零件都未发生失效，才可认为该种零件在置信度为 时具有 可靠性。
06、小结
1)在可靠性试验中，我们关心零件或系统的总体参数，但是可靠性试验不可能覆盖所有的零件，只能从总体 个零件中抽取 个零件作为样本，利用样本提供的信息来推断总体特征。
2)通常用样本统计量加减抽样误差来给出总体参数的一个估值范围，这就叫做总体参数的区间估计。由样本统计量所构造的总体参数的估计区间，称为置信区间。
3)重复多次构造置信区间，置信区间中包含总体参数真值的次数所占的比率，称为置信度，也叫做置信水平。置信水平一般用 来表示，其中 叫做显著性水平。
4)我们在进行可靠性试验，有时需要进行假设检验。所谓假设检验，就是首先提出一个对总体参数的假设，然后根据样本观察值对中这个假设进行判断，决定是接受还是拒绝原假设。假设检验的基本思想是统计学的小概率反证法。
5)对于假设检验，显著性水平和置信水平的定义略有变化。此时显著性水平指的是在原假设为真时，我们作出了拒绝原假设判断的概率的预设上限值。即弃真错误概率预设上限。
6)对于假设检验结果，我们不仅可以根据拒绝域进行决策，也可以利用P值进行决策。P值方法能够给出犯错实际概率，目前基本上取代了传统的拒绝域方法。
7)零件的可靠度检验一般采用二项检验法，零件的检验结果服从二项分布，我们可以建立可靠度、样本容量、置信水平和失效次数之间的关联。
作者简介
王朋波，清华大学力学博士，汽车结构CAE分析专家。重庆市科协成员、《计算机辅助工程》期刊审稿人、交通运输部项目评审专家。专业领域为整车疲劳耐久/NVH/碰撞安全性能开发与仿真计算，车体结构优化与轻量化，CAE分析流程自动化等。
最新资讯
-
中汽中心工程院能量流测试设备上线全新专家
2025-04-03 08:46
-
上新｜AutoHawk Extreme 横空出世-新一代实
2025-04-03 08:42
-
「智能座椅」东风日产N7为何敢称“百万级大
2025-04-03 08:31
-
基于加速度计补偿的俯仰角和路面坡度角估计
2025-04-03 08:30
-
《北京市自动驾驶汽车条例》正式实施 L3级
2025-04-02 20:23
