广告
高速永磁同步电动机铁耗分析
2022-01-27 23:45:25· 来源：EDC电驱未来
作者：戈宝军， 罗前通丨哈尔滨理工大学摘 要:为分析高速永磁同步电动机定子各区域的铁耗分布情况，研究一个周期内各个区域径向磁密和切向磁密的变化规律，采用
作者：戈宝军， 罗前通丨哈尔滨理工大学
摘 要:
为分析高速永磁同步电动机定子各区域的铁耗分布情况，研究一个周期内各个区域径向磁密和切向磁密的变化规律，采用不同的铁耗计算模型计算出定子铁心各区域铁耗的分布特性，将定子铁耗计算结果与有限元计算结果相比较，并进一步分析高速永磁同步电机的铁耗密度分布特点。计算结果表明，高速永磁同步电机稳定运行在较高的频率时，定子铁心中的涡流损耗占总铁心损耗的比重最大，附加损耗占比最小。当考虑旋转磁场和谐波分量的影响时，定子铁心损耗的大小明显高于仅考虑交变磁场影响时的损耗，更接近有限元计算结果。虽然定子齿顶的铁耗最小，但该区域的损耗密度最大，此外，定子铁心的各个区域还存在大量的谐波铁耗。
0 引 言
高速永磁同步电机功率密度高，效率高，体积小，重量轻，可靠性好。因此，高速永磁同步电机在运动控制和驱动系统等领域得到广泛应用。高速永磁同步电机应用在空气循环制冷系统、离心机、高速飞轮储能系统、轨道交通及航天等领域中，将会有良好的前景。
高速永磁同步电机有两个主要特点。一是转子的速度非常高，其转速一般在12 000 r/min以上。二是定子电枢绕组电流和定子铁心中磁通密度具有较高的频率。因此，导致定子铁耗、绕组铜耗和转子表面的涡流损耗大幅增加，由于高速永磁同步电机体积小，热源密度大，其散热比常规电机困难，可能导致永磁体不可逆退磁，还有可能导致电机内的温升过高，从而损坏电机内的绝缘。
高速永磁同步电机属于紧凑型电机，因此，在电机的设计阶段对各种损耗的精确计算是有必要的。在高频供电方式下，定子铁心损耗较高，因此研究高速永磁同步电机的定子铁心损耗是非常必要的。
在本文中，根据高速永磁同步电机的设计方案，建立了其二维有限元分析模型，并对电机的定子铁心区域进行划分，分析了各个区域中典型位置径向磁密和切向磁密的变化规律，考虑了谐波及旋转磁化的影响，分析了各区域的损耗分布规律并将计算结果与使用传统的三项式模型的计算结果进行了比较。
1 高速永磁同步电机有限元模型的建立
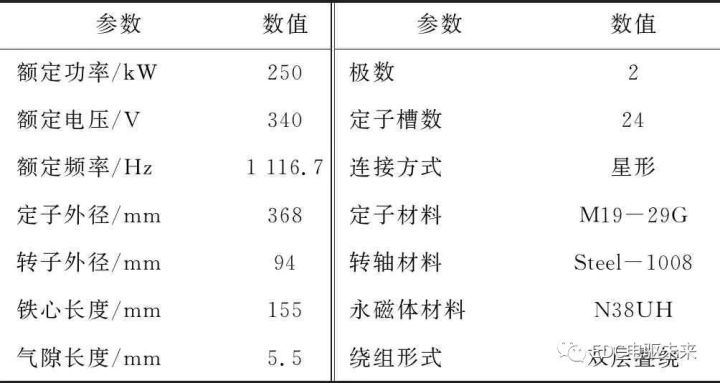
本文以一台额定输出功率为250 kW的2极24槽高速永磁同步电机为例，其额定转速为67 002 r/min。建立高速永磁同步电动机的二维有限元模型。该电机的基本参数如表1所示。
在高速永磁同步电机内电磁分布比较复杂，确立一些适当的假设条件，不仅不会影响计算结果的准确性，还会大大提高计算速度，节省计算资源。本文在建模过程中，对高速永磁同步电机做出如下假设：
1)假设该电机内的电磁场在轴向上保持恒定，因此，将电机的有限元模型简化为二维模型；
2)简化电机的端部效应，将其等效为电感和电阻的形式，并计入定子电枢绕组中；
3)电机内电磁场是似稳场，忽略位移电流；
4)由于实际中电机铁心外部磁场占比较小，本文忽略电机铁心外部的磁场，假设定子外圆理想磁绝缘。
表1 高速永磁同步电机的基本参数
Table 1 Basic parameters of high-speed permanent magnet synchronous motor
基于以上假设条件，为了对高速永磁同步电机的瞬态磁场进行求解，取该电机定子外圆所包含的部分作为求解域，可以建立该电机的二维有限元计算模型，如图1所示。由于高速永磁同步电机的温升问题一直是学术界研究的难题，本设计方案为了更好地加强电机的散热效果，定子槽型采用“棒槌槽”。
图1 高速永磁同步电机有限元计算模型
Fig.1 Finite element calculation model of high-speedpermanent magnet synchronous motor
在对高速永磁同步电机进行有限元计算时，需要对求解域施加边界条件。在求解区域内，采用矢量磁位求解，矢量磁位Az满足方程：
(1)式中：Az为矢量磁位的z轴分量；S1为定子外边界；Jz为源电流密度；μ为材料的磁导率；σ为材料的电导率。
2 高速永磁同步电机定子铁耗计算
2.1 高速永磁同步电机定子铁耗计算模型
准确计算高速永磁同步电机定子铁心损耗对电机性能和温度场分析非常重要。高速永磁同步电机在工作时，定子铁心各点磁通密度的波形是非正弦和非线性的，且磁密谐波含量较大。通常旋转电机铁心包含交变磁场和旋转磁场，因此，难以准确计算定子铁耗。
为了准确地计算定子铁耗，国内外的许多学者已进行了大量的研究，并提出了多种铁耗的计算模型。
1）在课程教学中不断进行反思，即在课程教学进行的每个节段反思理论知识是否讲解明确，与工程实践的联系是否紧密，是否提高了学生的学习兴趣，是否满足教学计划，等等。通过在教学过程中不断反思，不断修正后续课程教学内容，使教学效果不断优化。
PFe=Ph+Pc+Pe=
(2)式中：PFe为铁心损耗；Ph为磁滞损耗；Pc为涡流损耗； Pe为附加损耗； Bm为铁心磁通密度幅值； f为频率；kh、x为磁滞损耗系数；kc涡流损耗系数； ke为附加损耗系数。
由于上述Bertotti铁耗分立计算模型仅考虑交变磁场的影响，没有考虑谐波和旋转磁场的影响，因此，在计算高速永磁同步电机的铁耗时往往会导致很大误差。为了准确地计算高速永磁同步电机的铁耗，可以根据谐波分析原理，电机中任意一点磁密波形傅里叶展开后都可以分解为基波和一系列的谐波分量，此时，铁心损耗等于铁心磁密基波和铁心磁密各次谐波分量产生的铁耗之和。当考虑铁心中旋转磁场的影响时，由于铁心磁密中的每一个k次谐波分量的旋转磁场是椭圆形，因此，可以将椭圆形旋转磁场分解为2个相互正交的交变磁场，所以，椭圆形旋转磁场的总铁耗就等于径向和切向上的交变磁场产生的铁耗之和。因此，定子铁心磁滞损耗计算模型的表达式为
(3)定子铁心涡流损耗计算模型的表达式为
(4)定子铁心附加损耗计算模型的表达式为
(5)式中Brk、Btk分别为铁心径向和切向磁通密度的第k次谐波分量的幅值。
由上述所建立的铁耗计算模型的表达式可知，铁耗主要取决于铁心材料的损耗系数、铁心磁通密度及频率。其中，损耗系数kh、x、kc和ke可由铁心材料的损耗曲线拟合得到。
2.2 定子铁心磁通密度的有限元分析
永磁同步电机定子铁心各部位磁通密度的幅值和磁通密度的变化规律是不同的，如果在计算定子铁耗时，带入定子铁心的平均磁通密度会影响计算结果的精度。理论上为了能准确地计算定子铁耗需要确定定子铁心内各部位磁通密度的分布及变化规律，因此需要在定子铁心上取几个典型位置并分别求解各位置的磁通密度及变化规律。
为了准确地计算定子铁耗需要对定子铁心进行区域划分，如图2所示，则定子铁耗为各区域铁耗之和。由于定子槽型采用的并非传统的槽型，其定子齿的长度较大，需要对齿部进行细化分析，因此，在图2中将定子铁心分为齿顶、通风沟齿、电枢绕组齿、齿部和轭部的交界处、轭部5个区域，并分别在这5个区域中取点A、B、C、D、E，通过分析选取点A、B、C、D、E的磁通密度来等效其所在区域的磁通密度。
图2 定子铁心区域划分
Fig.2 Region division of stator core
当电机在额定转速下稳定运行时，定子铁心5个不同位置径向磁密与切向磁密随电角度变化的波形及磁通密度轨迹如图3所示，其中，径向磁密用 Br表示，切向磁密用Bt表示。
图3 定子铁心不同位置磁密波形及磁密轨迹
Fig.3 Magnetic flux density waveform and trackat different positions of stator core
由图3可知，高速永磁同步电机定子齿的齿顶部位的磁化方式主要受交变磁场的影响，旋转磁场对齿顶的磁化方式影响较小。B点和C点磁密轨迹近似为一条直线，因此，B点、C点磁化方式主要以交变磁化为主，且几乎不受旋转磁场的影响，所以，定子齿身的磁化方式可近似的认为是交变磁化方式。D点磁密轨迹为一个近似的椭圆形，因此齿部和轭部的交界处受旋转磁场的影响较大。E点的磁化方式虽受旋转磁场和交变磁场共同影响，但由于该点切向磁密分量远大于径向磁密，说明定子铁心轭部主要受交变磁场的影响。
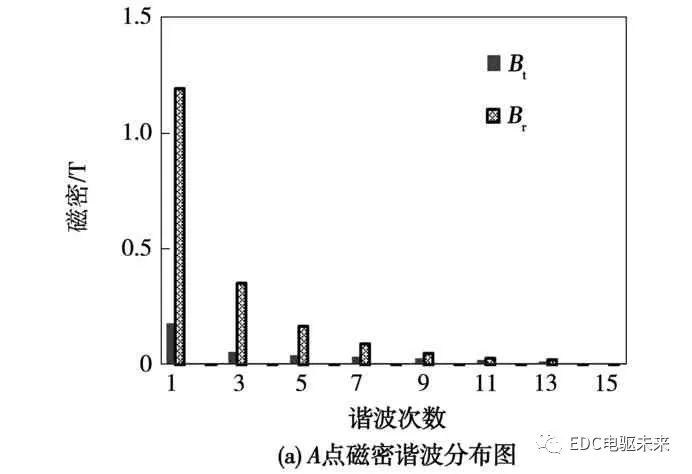
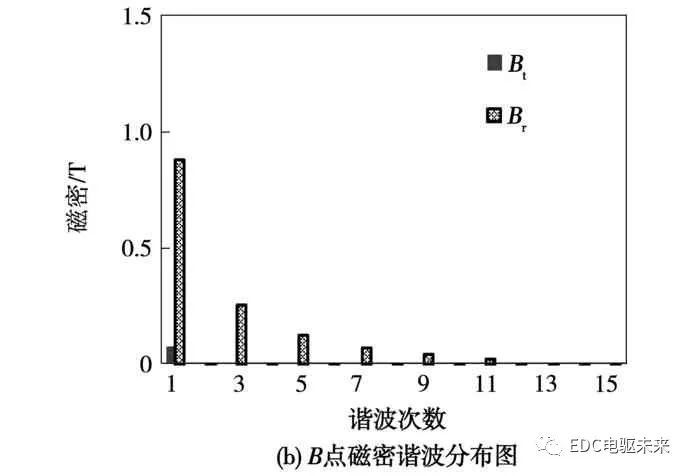
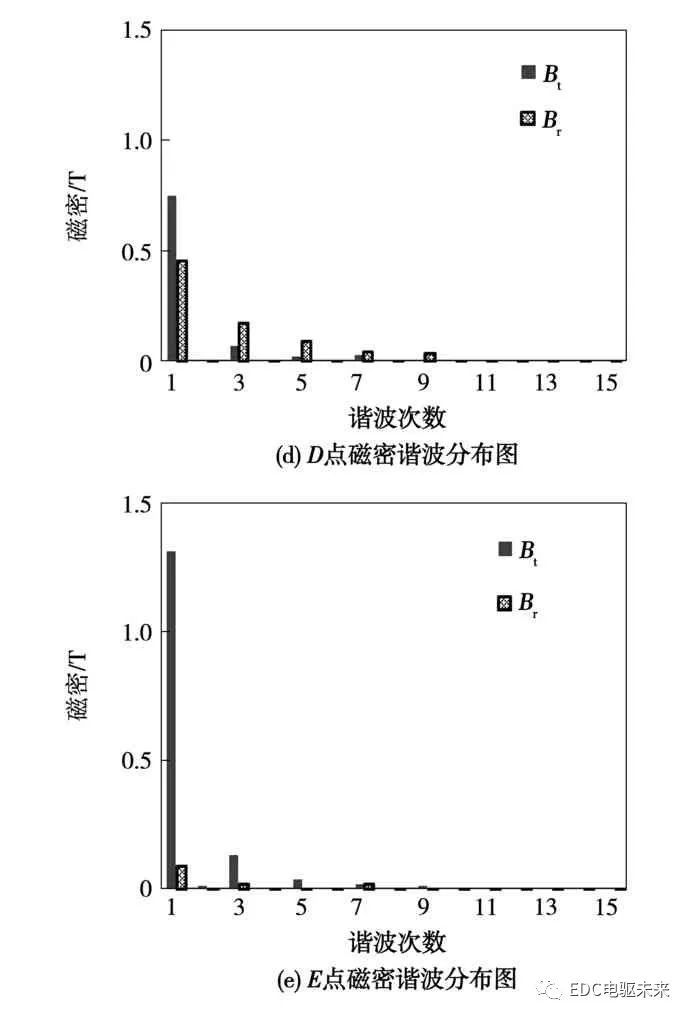
由图3可知，A、B、C、D、E各点的径向磁通密度与切向磁通密度在一个周期内呈非正弦分布，因此各点的磁通密度中含有一定的谐波分量，因此需要将各点的径向磁密与切向磁密进行谐波分解。各点的径向磁密与切向磁密的基波和各次谐波幅值的变化规律如图4所示。
从图4中可以看出，A点径向磁密的基波幅值最大，最大值为1.19 T；E点径向磁密的基波幅值最小，最小值为0.09 T；E点切向磁密的基波幅值最大，最大值为1.3 T；C点切向磁密的基波幅值最小，最小值为0.04 T。此外，A、B、C三点的径向磁密的基波幅值明显大于其对应切向磁密的基波幅值。D、E两点的切向磁密的基波幅值大于其对应径向磁密的基波幅值。同时，由计算结果可知各点磁密中3、5、7次谐波含量较大。因此，在计算高速永磁同步电机的定子铁心损耗时不仅要计算交变磁场产生的铁耗，还应考虑谐波与旋转磁场对铁耗的影响。
图4 定子铁心不同位置磁密谐波分布图
Fig.4 Magnetic flux density harmonic distribution atdifferent positions of stator core
3 不同方案下铁耗结果分析
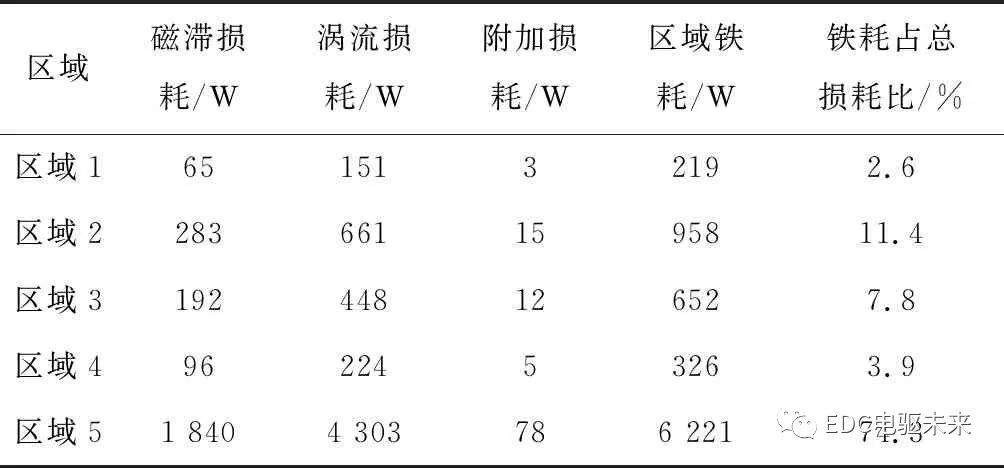
本文采用3种方案计算高速永磁同步电机在额定负载时的定子铁耗。方案1是只计算定子铁心中交变磁场产生的铁耗，并根据式(2)求出该方案下的铁耗；方案2是不仅计算定子铁心中交变磁场产生的铁耗还计算定子铁心中谐波和旋转磁场产生的铁耗，并根据式(3)～式(5)求出该方案下的铁耗；方案3是基于时步有限元理论计算铁耗，并利用有限元仿真计算该方案下的铁耗。计算结果如表2～表5所示。表2～表4中各区域的“铁耗占总损耗比”指定子各区域铁心损耗占定子铁耗的比重。
表2 方案1定子铁耗计算结果
Table 2 Solution 1 calculation results of stator iron loss
由3种方案的铁耗计算结果可知，高速永磁同步电机稳定运行在较高的频率时，定子铁心中的涡流损耗占总铁心损耗的比重最大，附加损耗占比最小。此外，对比分析方案1与方案2铁耗计算结果可得，采用方案2计算的各区域磁滞损耗、涡流损耗、附加铁耗明显大于采用方案1计算的各区域对应铁耗。因此，当考虑旋转磁场和谐波分量对定子铁心损耗的影响时，定子损耗的计算结果明显高于仅考虑交变磁场影响时的计算结果。由表2与表3中的数据还可看出，方案1中各区域铁耗占总铁耗的比例与方案2中相对应的铁耗比例是不同的，方案1中定子轭部的铁耗比例大于方案2定子轭部的铁耗比例，而方案1定子铁心其它区域的铁耗比例则小于方案2相应区域的铁耗比例。这是因为定子轭部磁密分量主要以切向磁密分量为主且切向磁密分量中谐波含量较低，而其它区域中的磁密谐波含量较大。因此，当考虑谐波磁通与旋转极化时，定子铁心轭部的铁耗比例减小。通过对表3与表4中的数据分析可得，采用方案2与方案3所得的定子轭部铁心损耗在总损耗所占比例均为最大，分别是58.7%、56.6%，且2种方案下的所占比例相近。而定子齿顶铁心损耗在总损耗所占比例均为最小，分别是3.3%、4.4%，且2种方案下的所占比例相近。同时，在方案2中，其它各区域的铁心损耗在总损耗中所占比例与方案3的计算结果相近。
表3 方案2定子铁耗计算结果
Table 3 Solution 2 calculation results of stator iron loss
表4 方案3定子铁耗计算结果
Table 4 Solution 3 calculation results of stator iron loss
表5 高速永磁同步电机铁耗计算结果比较
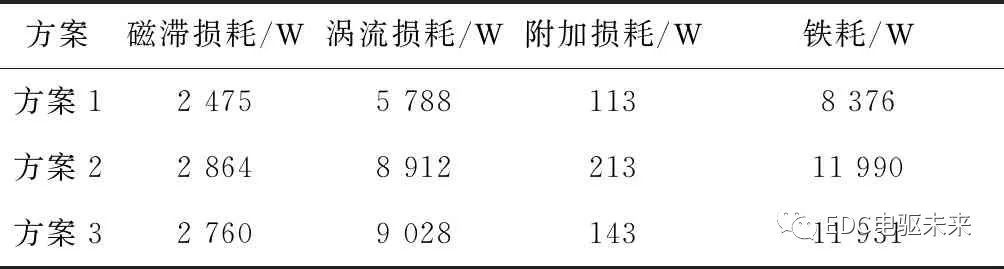
Table 5 Comparison of calculation results of iron loss in high-speed permanent magnet synchronous motor
通过表5分析得出，采用方案1计算的定子铁心磁滞损耗、涡流损耗、附加损耗与有限元计算相应损耗的差值较大，精度较低。而方案2的磁滞损耗、涡流损耗、铁心损耗的计算结果接近于有限元计算对应损耗的计算结果，精度较高。因此，在计算定子铁心损耗时不仅要计算交变磁场产生的铁耗还计算定子铁心中谐波和旋转磁场产生的铁耗。
4 定子铁心不同区域铁耗密度分析
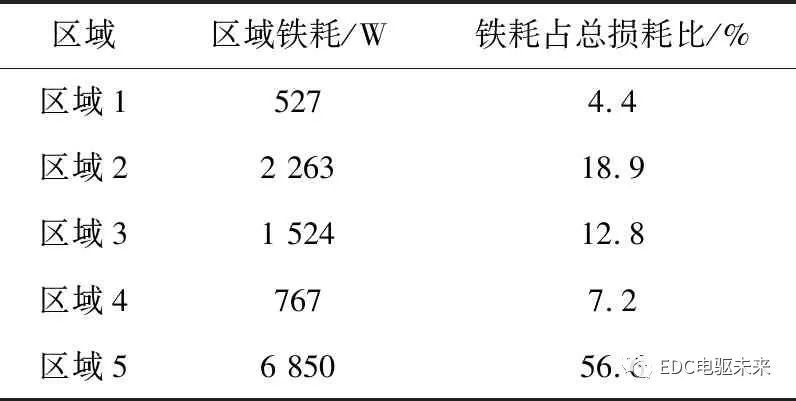
由文献[8]可知，异步电机定子齿顶的铁耗密度最大，对于高速永磁同步电机铁耗密度的分布，国内学者研究较少，因此有必要进一步研究高速永磁同步电机铁耗密度分布，为后续高速永磁同步电机设计提供依据。各区域铁耗密度分布如表6所示。
表6 定子铁心不同区域铁耗分布
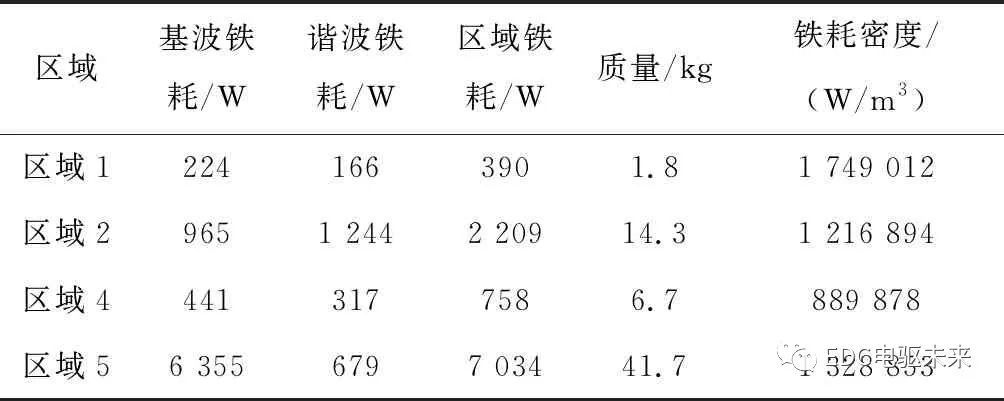
Table 6 Iron losses distribution in different regions of stator core
由表6的数据可以看出，高速永磁同步电机定子铁心各区域铁耗分布由小到大依次为区域1、区域4、区域3、区域2及区域5，分别对应于图2定子齿顶、齿部和轭部的交界处、电枢绕组齿、通风沟齿、定子轭部。虽然定子齿顶的铁耗最小，仅占总铁耗的3.3%，但定子齿顶的铁心重量为1.8 kg，占定子铁心总质量的2.1%，因此，该区域的损耗密度最大，约为整个定子铁心平均损耗密度的2.25倍。由于区域3的铁心质量为20.4 kg，占定子铁心总质量的24%，且该区域的铁心损耗为758 W，占总铁耗的6.3%，故该区域的铁耗密度最小。此外，从表6中的数据还可看出，定子铁心的各个区域存在大量的谐波铁耗。因此，在对高速永磁同步电机设计时，应当抑制定子铁心中谐波磁通的产生，从而减少谐波铁耗的产生，这对降低电机温升是很有意义的。此外，本文阐述的3种方法计算铁心损耗的结果主要取决于各区域的磁密和电机的结构，与运行特点无关。不仅适用于高速永磁同步电机，对其他电磁原理的旋转电机同样适用。
5 结 论
本文以一台额定功率为250 kW，额定转速为67 002 r/min的高速永磁同步电机为例，建立了其二维有限元计算模型，并将不同铁耗模型的计算结果进行了比较，同时，分析了各区域的损耗分布规律，并得出以下结论：
1)通过对高速永磁同步电机的定子铁心中磁密的有限元分析可知，定子铁心中的磁密波形非常复杂，铁心磁密含有一定的谐波分量。定子铁心各个区域的磁化方式各不相同，定子齿顶部位的磁化方式主要以交变磁化为主；定子齿身的磁化方式可近似的认为是交变磁化方式；定子齿部和轭部交界处的磁化方式受旋转磁场的影响较大；定子铁心轭部的磁化方式主要受交变磁场的影响。
2)高速永磁同步电机稳定运行在较高的频率时，定子铁心中的涡流损耗占总铁心损耗的比重最大，附加损耗占比最小。
3)当考虑旋转磁场和谐波分量对定子铁心损耗的影响时，定子铁耗的计算结果明显高于仅考虑交变磁场影响时的计算结果，更接近有限元计算结果。因此，在计算定子铁心损耗时不仅要计算交变磁场产生的铁耗还要计算定子铁心中谐波和旋转磁场产生的铁耗。
4)高速永磁同步电机定子铁心各区域铁耗分布由小到大依次定子齿顶、齿部和轭部的交界处、电枢绕组齿、通风沟齿、定子轭部，受谐波磁通的影响，虽然定子齿顶的铁耗最小，但该区域的损耗密度最大。此外，定子铁心的各个区域存在大量的谐波铁耗。
本文摘自《电机与控制学报》
广告 
广告
编辑推荐
最新资讯
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
-
车载无线广播收音机还需要吗？
2024-12-23 07:37
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
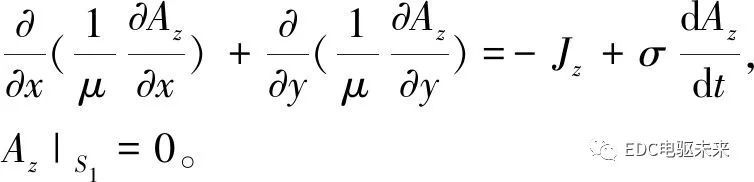
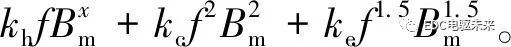
广告
广告
