广告
行星轮系的杠杆分析法介绍
2022-02-03 21:20:14· 来源：汽车动力总成
一、杠杆分析法的产生背景行星齿轮机构是AT自动变速箱中的常用元件，通过控制不同行星齿轮排间的元件的连接和分离，可以实现变速箱的不同传动比。由于行星齿轮机
一、杠杆分析法的产生背景
行星齿轮机构是AT自动变速箱中的常用元件，通过控制不同行星齿轮排间的元件的连接和分离，可以实现变速箱的不同传动比。由于行星齿轮机构可以在极紧凑的空间内实现非常大的传动比，因此还被广泛的使用在诸如E-CVT变速箱和EV的减速机构中。
图1 AT自动变速箱中的行星齿轮机构
图2 GKN开发的EV用第三代eAxle中使用了行星轮系
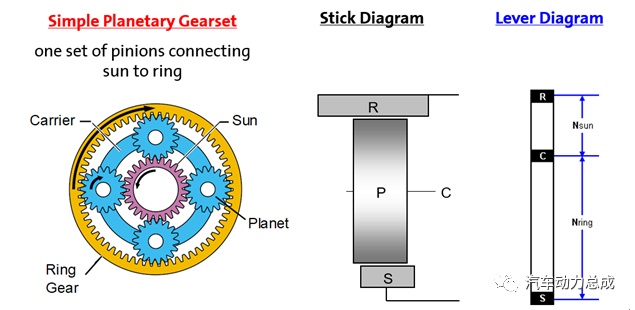
一个典型的行星排包括太阳轮、行星架、行星轮和齿圈，其中行星轮固定在行星架上，可以围绕行星架上的固定轴做自转运动，还可以绕太阳轮或齿圈做周转运动的同时。进行运动学和动力学分析时，常针对太阳轮、行星架、和齿圈三个元件。在行星排中，第三个元件的转动状态决定于另外两个元件的转动状态。在进行运动分析时，主体思路是利用牵连运动将周转运动转化为定轴轮系，使用解析法进行计算。
图4 单行星轮的行星排和双行星轮的行星排
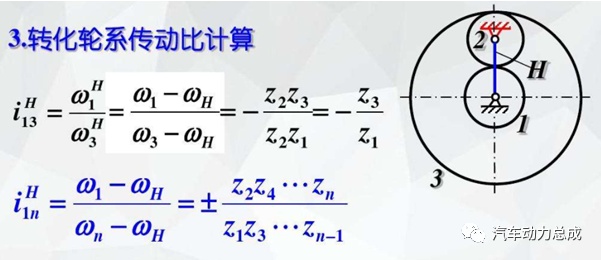
解析法需要将整个行星轮系参考行星架的运动假设进行转化，然后计算出所需的传动关系。随着自动变速箱内部行星齿轮排数量的增加，和组合方式复杂程度的不断提高，尤其是单向离合器或可选单向离合器的增加，用传统的解析法来计算扭矩和转速，存在繁琐、易出错, 不直观等问题, 很难让人们对行星齿轮组建立清晰的概念。下图展示了传统的解析法计算过程。
图5 传统的行星轮系解析法计算过程
GM在80年代就已经意识到这个问题，并开发了杠杆法对行星轮系机构进行转化和分析，可以通过杠杆分析法进行变速箱行星轮系机构的设计，分析和优化，还可以利用此方法对离合器的布置和控制方案进行优化选型。这个方法简单易用，目前已经被广泛应用于多行星轮系机构的设计开发中。杠杆法，简单来说就是将复杂的旋转运动转化为人们熟悉的直线运动。用杠杆来进行模拟和转化，可以对行星轮系机构进行更加直观的观察和分析。
二、行星轮系与杠杆之间的转化
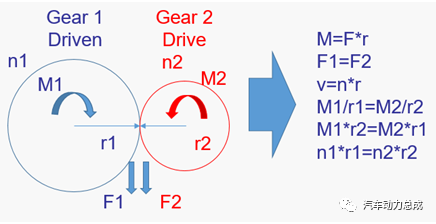
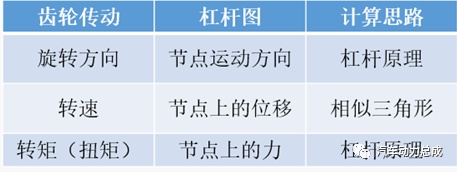
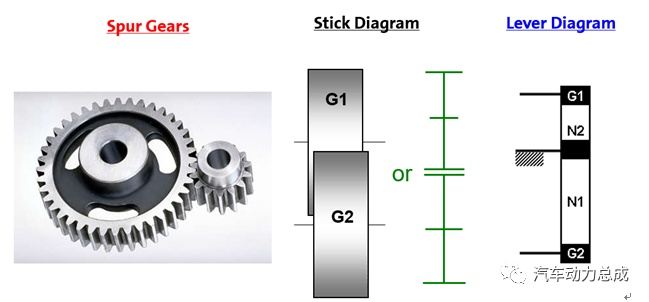
首先将外啮合定轴轮系齿轮传动的运动关系和受力关系罗列如下。
图6 传统的行星轮系解析法计算过程
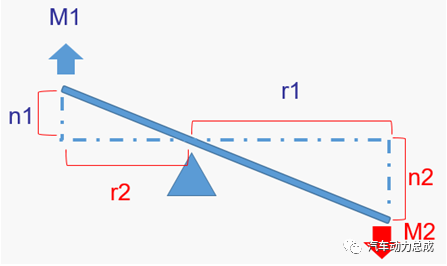
可以得到M1*r2=M2*r1和n1*r1=n2*r2两个公式，而且可以发现，M1、M2、r1、r2四个参数的关系恰好与杠杆运动中杠杆左右两端的力和位移及力臂之间的关系相似。因此，可以将上述定轴轮系中的各个参数位置按照如下关系带入到一个杠杆模型中，得到一个同时满足上述定轴轮系运动学和力学公式关系的杠杆。
图7 定轴外啮合齿轮副转化为杠杆
在这个杠杆中，原作用在主动和从动齿轮上的扭矩M1和M2被放置在杠杆的两侧作为力，由于外啮合齿轮的主从动齿轮力矩方向是相反的，所以力的方向也是相反的；利用齿轮的分度圆半径来绘制杠杆的左右端（力臂），其中r2作为M1的力臂，r1作为M2的力臂；杠杆两端的位移使用原主动和从动齿轮的转速进行等效替代；如果考虑到时间因素，也可以把这杠杆两段的位移等效为主从动齿轮转动的圈数。
根据杠杆的原理，利用相似三角形的计算规则，在左右力臂关系已知的情况下（由于齿轮齿数关系或传动比大小已知），通过杠杆一端的施力方向和大小可以计算出杠杆的另一端的受力大小和方向，也就是等效为待计算齿轮上的扭矩大小的转动或受力方向。
如上所述，可以得到定轴轮系和杠杆之间的转化关系表如下。
图8 定轴轮系和杠杆之间的转化关系
外啮合齿轮副转化为杠杆的过程
图9 外啮合齿轮副转化为杠杆的过程
单行星轮行星排转化为杠杆的过程
图10 单行星轮行星排转化为杠杆的过程
双行星轮行星排转化为杠杆的过程
图11 双行星轮行星排转化为杠杆的过程
由两个行星排组成的行星轮系转化为杠杆的过程
图12 两个行星排组成的行星轮系转化为杠杆的过程
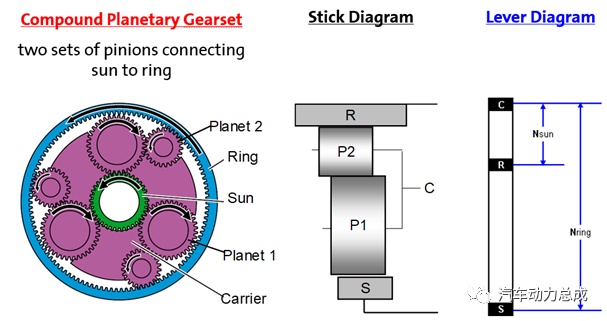
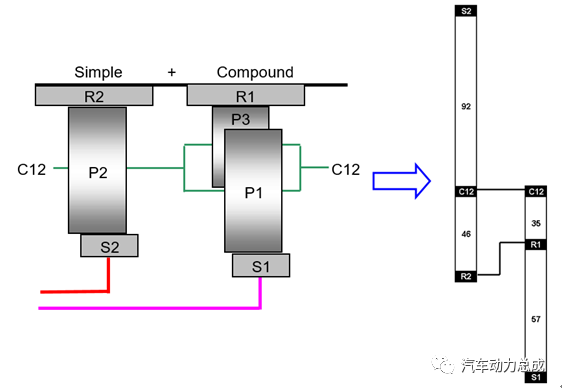
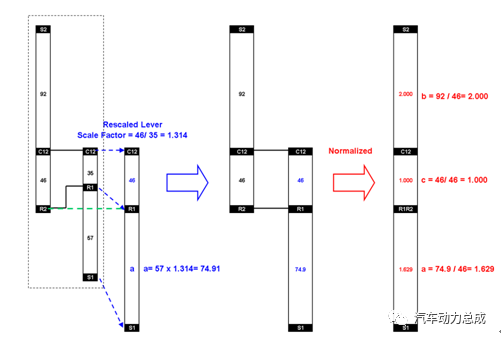
由于同一个行星排中，可以用齿轮的齿数来替代齿轮的半径或分度圆之间的比例关系，所以在对由两个行星排组成的行星轮系进行杠杆转化的过程中，可以先将两个行星排按照各自的齿轮齿数关系分别进行杠杆的转化，然后将存在硬连接的元件用实线连接起来（实线表示被连接的元件的受力和运动状态都是一致的）。由于代表两个行星排的力臂的齿轮齿数并不可能恰好一致，因此还需要通过等比放大的原则进行转化，才能让完整杠杆机构的比例关系正确；同时，如果相邻两个杠杆上存在两个实线连接的元件，则可以将这个两个杠杆进行合并，最终得到下图右侧的综合杠杆。
最终将最初复杂的双行星排轮系转化成为一个简单的杠杆。大大简化了复杂行星轮系的分析过程。
图13 两个行星排组成的行星轮系转化为杠杆的过程
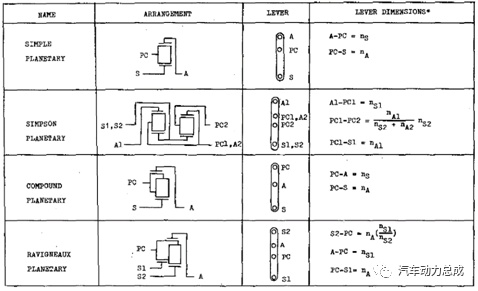
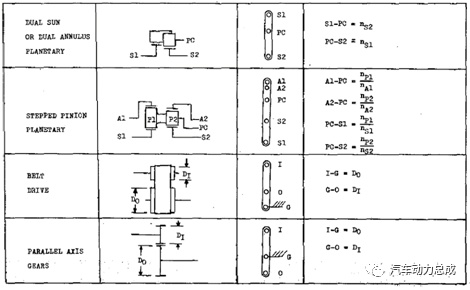
根据上述转化原理和关系，可以将常见的行星排模块与杠杆之间的转化关系汇总如下表所示。同时，通过这些基本模块之间的组合，可以实现各种复杂轮系向杠杆的转化。
图14 常见行星排模块与杠杆之间的转化
三、使用杠杆法对典型自动变速箱进行机构转化
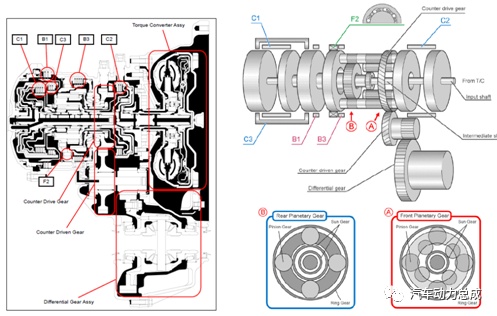
下图是一款4AT自动变速箱的剖面图和结构图，变速箱的行星轮系由前后两个行星排组成，采用典型的拉维娜式结构设计，特点是结构紧凑、齿轮接触面积较大，可以由太阳轮、行星架或齿圈作为输出元件。其中A行星排是双行星轮结构，B行星是单行星轮结构，两个行星排有各自单独的太阳轮，公用齿圈，且B行星排的行星轮是A行星排的行星轮之一。拉维娜式行星齿轮机构及其变形被广泛的使用在各类自动变速箱中。
图15 某4AT自动变速箱的结构简图
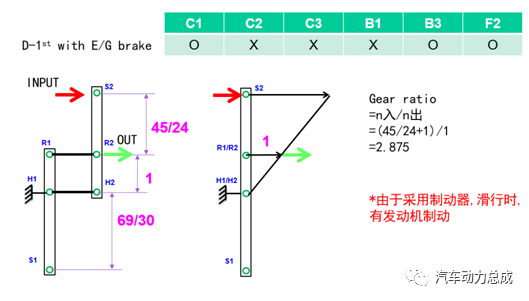
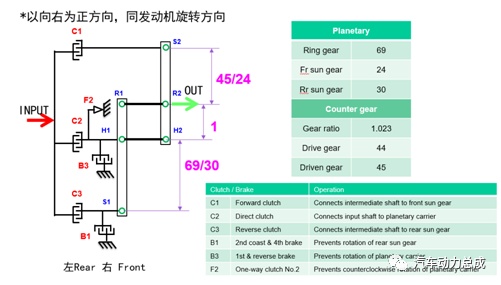
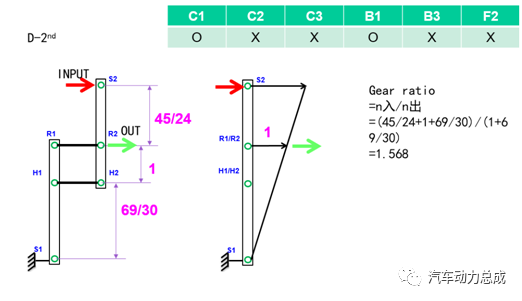
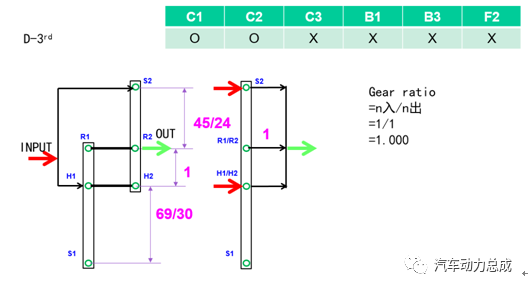
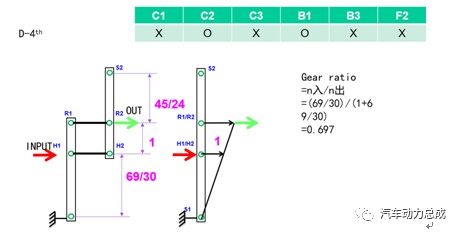
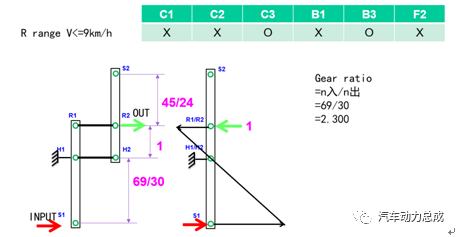
定义杠杆向右为正方向，与发动机的旋转方向相同，根据A/B行星排齿轮的齿数和元件之间的连接关系，以及离合器的布置位置，绘制杠杆图如下。
图16 根据齿轮齿数信息和离合器布置位置绘制杠杆图
四、使用杠杆法进行挡位分析和速比计算
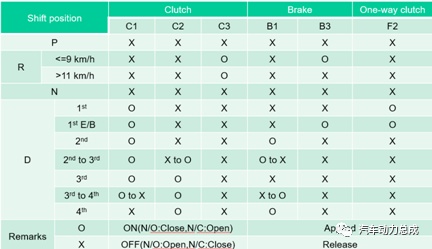
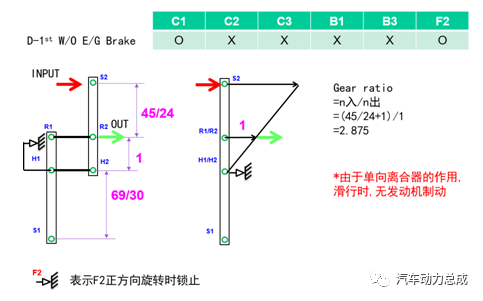
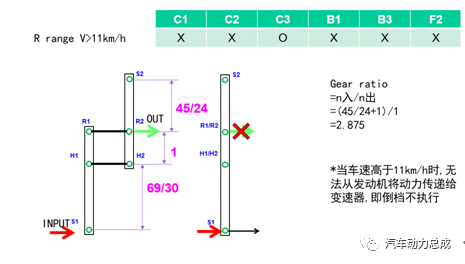
该变速箱的挡位逻辑图如下（由于P/N挡较简单，不单独绘制杠杆图）
图17 某4AT自动变速箱挡位逻辑图
1挡无发动机制动时的运动状态和速比
1挡有发动机制动时的运动状态和速比
2挡时的运动状态和速比
3挡时的运动状态和速比
挡时的运动状态和速比
R挡时的运动状态和速比，车速低于9km/h时
R挡时的运动状态和速比，车速高于11km/h时
五、总结使用杠杆法进行挡位分析和速比计算
杠杆法是一种高效的行星轮系的等效计算方法, 它可以将复杂的行星轮系转化成等效的杠杆图, 使行星轮系中各个元件的受力分析和运动简单直观，可以快速地对自动变速箱的工作状态进行分析, 有助于深入地了解自动变速箱的工作原理以及进行新的行星轮系传动机构的开发。
广告 
广告
编辑推荐
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
广告
广告
