广告
减振器支柱总成衬套对整车NVH性能影响的研究
2022-02-08 22:03:53· 来源：ATC汽车底盘
摘要：悬架总成中的橡胶衬套作为悬架系统各构件的连接元件，对悬架及整车的NVH 性能有很大影响。建立含减振器支柱总成橡胶衬套及不含相应衬套的整车振动系统数学
摘要：
悬架总成中的橡胶衬套作为悬架系统各构件的连接元件，对悬架及整车的NVH 性能有很大影响。建立含减振器支柱总成橡胶衬套及不含相应衬套的整车振动系统数学模型，求解得到，橡胶衬套可有效地改善整车的NVH 性能；基于ADAMS/CAR 建立整车平顺性仿真模型，仿真结果验证了数学模型及分析结果的准确性；基于该数学模型采用灵敏度分析方式研究不同连接处衬套刚度对整车振动响应的影响并进行优化设计，结果表明，优化衬套刚度可进一步提升整车的NVH 性能。研究结果对整车NVH 性能的优化设计具有一定的参考意义。
引言
汽车悬架作为底盘系统的关键部件，起着衰减路面激励的重要作用，其性能的好坏决定着整车的操纵稳定性、平顺性及NVH（Noise、Vibration、Harshness）性能。影响悬架性能的因素很多，橡胶衬套作为悬架系统各构件的连接元件，是影响悬架性能的重要因素之一。橡胶衬套主要是用于约束悬架构件间的相对运动、缓冲各构件之间的振动冲击以及弥补装配制造误差等。
因此，研究悬架衬套对整车及悬架性能的影响，对提高车辆的NVH 性能有着重要的实际意义。以某款开发中的车型为研究对象，建立包含减振器支柱总成各连接衬套（减振器连接车身衬套、弹簧连接车身衬套、减振器底部衬套）的整车数学理论模型，通过整车动力学仿真验证理论模型的正确性，并在此基础上优化相关衬套刚度，提升该车型的NVH 性能。
多自由度整车理论模型的建立与求解
整车数学模型的建立
当前，对于橡胶衬套力学特性的研究主要有Kelvin-Voigt 理论、三参数 Maxwell 理论，BERG 理论、DZIERZEK 理论等四种半经验理论，综合分析各种理论模型的特点，基于其与整车振动分析模型结合的简洁性及有效性，选取刚度、阻尼相并联的Kelvin-Voigt 模型，建立考虑相应连接衬套的整车振动模型。所研车型前悬架为麦弗逊悬架，其减振器、弹簧及连接衬套组成减振器支柱总成，后悬架为多连杆悬架，弹簧独立于减振器安装在H 控制臂处。根据所研车辆的实际结构，建立包含减振器支柱总成各连接衬套的整车振动模型，如图1 所示。
图1 含衬套的整车振动模型
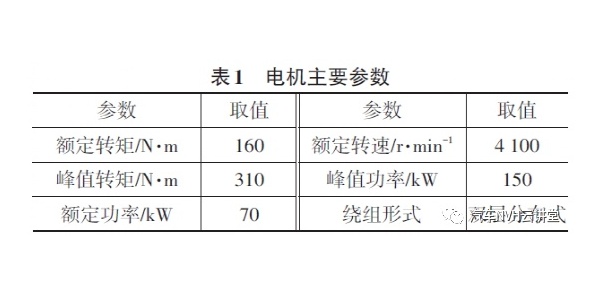
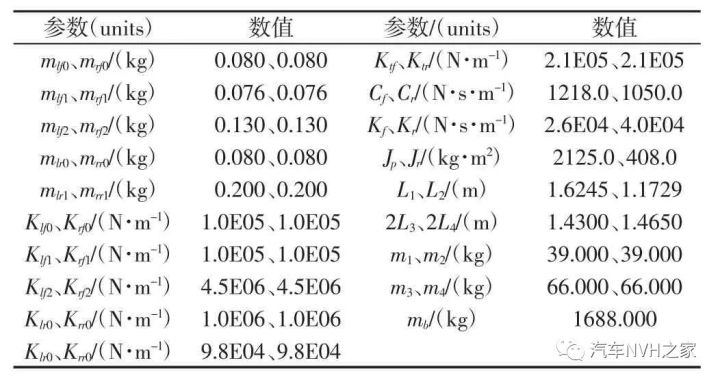
图中：X1、X2、X3、X4—与各车轮相对应的非簧载质量的垂向运动；Xb—车身垂向运动；Xp—车身前后俯仰运动；Xr—车身左右侧倾运动；Xlf0（Xrf0）、Xlf1（Xrf1）、Xlf2（Xrf2）—左（右）前弹簧连接车身衬套、前减振器连接车身衬套、前减振器底部连接衬套的垂向运动；Xlr0（Xrr0）、Xlr1（Xrr1）—左（右）后弹簧连接车身衬套、后减振器连接衬套的垂向运动；mlf0（mrf0）、mlf1（mrf1）、mlf2（mrf2）、mlr0（mrr0）、mlr1（mrr1）—左（右）前弹簧连接车身衬套质量、前减振器连接车身衬套质量、前减振器下端衬套质量、后弹簧连接衬套等效质量、后减振器连接衬套等效质量；m1（m2）、m3（m4）—左（右）前、后悬架的非簧载质量；mb—簧载质 量 ；Klf0（Krf0）、Klf1（Krf1）、Klf2（Krf2）、Klr0（Krr0）、Klr0（Krr0）—左（右）前弹簧连接车身衬套刚度、前减振器连接车身衬套刚度、前减振器下端衬套刚度、后弹簧连接衬套等效刚度、后减振器连接衬套等效刚度；Ktf、Ktf—前后轮胎的刚度；Cf、Cr—前后悬架阻尼系数；Kf、Kr—考虑了除减振器总成连接衬套外的其它衬套的前、后悬架等效刚度；Jp、Jr—俯仰、侧倾转动惯量；L1、L2—质心到前、后轴的距离；L3、L4—1/2 倍的前、后轮距；q1（t）、q2（t）、q3（t）、q4（t）—四个车轮所受的路面激励。整车模型中的参数值，如表1 所示。
表1 车辆模型参数
由于轮胎的阻尼相对于刚度对车辆性能的影响较小，在此模型中忽略不计，模型中所有衬套的阻尼参考相关文献[7]，一般取值为500N·m-1，则含橡胶衬套的整车振动模型可由以下微分方程矩阵形式来表示：
式中：M—质量矩阵；C—阻尼矩阵；K—刚度矩阵；—系统的固有特征矩阵，可分别由表1 中的质量参数、阻尼参数、刚度参数表示；X—位移矩阵；F—激励系数矩阵；q（t）—激励向量，其具体形式如下：
整车模型的求解
目前，对于路面激励的研究已经很成熟，在时域内对其有多种计算方法，采用滤波白噪声法来模拟路面不平度模型。
路面不平度对单个车轮产生的激励q（t）表示为：
式中：Gq（n0）—汽车行驶路面不平度系数，m2；n0—参考空间频率，为0.1m-1；n1—道路空间截止频率，为0.011m-1；v—跨界车行驶速度，m/s；w（t）—单位白噪声激励。
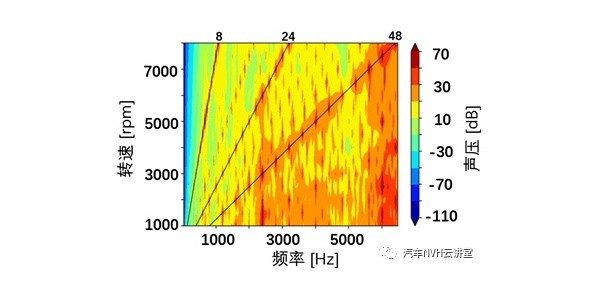
在汽车行驶的过程中，汽车左右轮存在相关性，前后轮存在延时性，具体关系见文献。选取B 级随机路面激励与v=60km/h作为输入条件，联立式（1），对考虑减振器支柱总成橡胶衬套的整车模型与不考虑相应衬套的整车模型进行求解，得到车身垂向加速度时频曲线，如图2 所示。
图2 车身振动加速度
在相同的路面激励下，含相应连接衬套的整车数学模型与不含各衬套的整车数学模型相比，车身垂向振动响应趋势基本一致，振动幅值有所降低，如图2（a）所示。通过计算两模型车身垂向加速度的均方根值，得含衬套与不含衬套模型的车身垂向振动响应均方根值分别为0.538m/s2、0.560m/s2，相对减小了3.93%；由图2（b）可以看出，两模型均在2Hz 附近（车身共振处）与12Hz 附近（车轮共振处）出现振动峰值，这与所研车辆的实际情况一致；从图中还可以看出，在（1～10）Hz 的低频段内两模型的垂向加速度功率谱密度基本一致，当频率大于 10Hz，主要在（50～90）Hz 的中高频率段内，含衬套模型的车身垂向振动明显低于不含衬套模型的车身垂向振动，说明减振器支柱总成衬套对衰减由路面激励产生的振动起着关键的作用，尤其对高速行驶车辆的中高频振动衰减作用更显著，这主要是因为减振器不容易衰减由路面产生的中高频激励，使较多的中高频振动能量传递至橡胶衬套，衬套通过自身的变形可吸收较多的能量达到衰减振动的效果，提升车辆高速行驶的平顺性和NVH 性能。
整车动力学仿真
为验证理论分析的正确性，利用ADAMS/CAR 软件建立整车的虚拟样机模型，进行整车平顺性仿真。所研究的车型，前悬架采用的是麦弗逊式悬架，后悬架采用的是H 臂型多连杆独立悬架，根据车辆部件的实际结构及相关硬点坐标，在ADAMS/CAR中分别建立前、后悬架仿真模型。由于需要分析含相应连接衬套与不含相应连接衬套的整车仿真模型，建立悬架模型时，在各连接处建立了刚性连接（在Attachments 模块下选择joint 选项，再根据不同连接处需要的运动副建立旋转福、hooke 副、圆柱副、球副等）与衬套连接（在Attachments 模块下选择bushing 选项，根据各衬套的属性设置参数，并设置衬套的激活状态，never 表示始终处于激活状态，kinematic mode 表示在运动学模式下处于抑制状态）。
采用机械式转向结构及F-tire 轮胎模型，车身参数由表1获得，建立各部件系统并选择ADAMS/CAR Ride 模块中的四立柱实验平台进行装配，得整车仿真虚拟样机模型，如图3 所示。
图3 整车平顺性仿真虚拟样机模型
当进行仿真时，可通过ADAMS/CAR 中Adjust 模块来调节选择刚性连接或衬套连接，即相应连接处是否含衬套。选取与理论计算一致的路面激励与速度进行整车的平顺性仿真，可得到与理论分析结果对应的车身垂向振动时频图。含衬套及不含衬套的车身垂向加速度时频响应曲线，如图4 所示。
图4 车身垂向加速度响应曲线
通过对比图4 与图2 的时频曲线，可以看出两模型的仿真时频图与理论时频图基本一致，均表明含衬套模型相较于不含衬套模型的车身垂向振动有所降低。
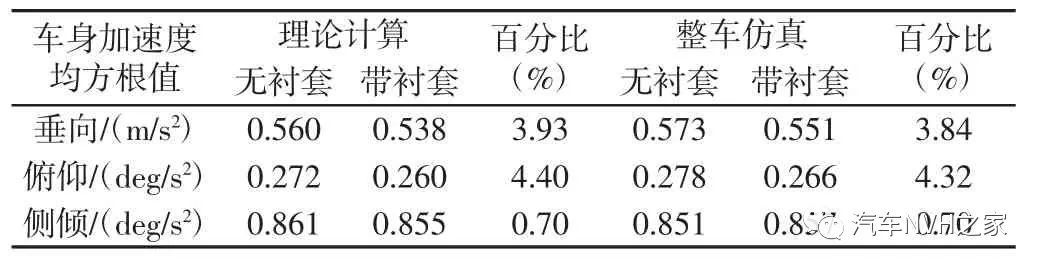
为了进一步验证理论模型的正确性，分别计算由仿真与理论得到的车身垂向、俯仰及侧倾加速度均方根值结果，如表2 所示。
表2 仿真与理论结果
由表2 可以看出，有、无衬套模型的理论计算与仿真分析结果的相关参数的均方根值及变化的百分比基本一致，表明所建立的考虑减振器支柱总成衬套的整车理论模型是正确可靠的，可用其进行衬套的优化设计研究，以提升整车NVH 性能。
衬套力学特性对整车NVH 影响的研究及优化
衬套力学特性对整车NVH 影响的研究
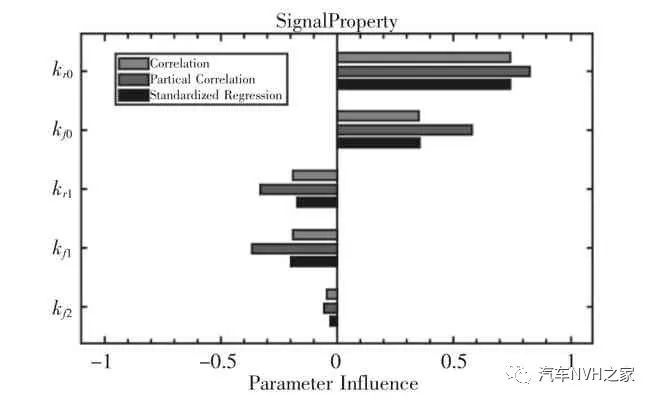
基于上述正确的整车模型，研究相关衬套参数变化对整车平顺性的影响，衬套的力学特性参数主要有阻尼特性和刚度特性，由于衬套阻尼的改变对车身参数几乎无影响，此处不作讨论。为了直观地观察衬套刚度变化对车辆平顺性的影响，此处基于Simulink 自带的优化工具箱，以车身垂向加速度均方根值最小为设计要求，以衬套刚度Kf0、Kf1、Kf2、Kr0、Kr0（Kf0=Klf0=Krf0，其余刚度类似）为设计变量进行灵敏度分析，考虑衬套刚度对平顺性与操纵性影响的矛盾性，其不能取太大与太小，此处取各衬套刚度的0.2 倍与5 倍作为设计变量的最小值与最大值，在每个刚度区间内通过随样抽样法产生100 个样本，计算结果，如图5 所示。
图5 衬套刚度对车辆平顺性的影响
图5 给出了由相关系数（Correlation）、偏相关系数（Partial Correlation）与标准回归系数（Standardized Regression）评价得到的灵敏度结果。相关系数绝对值越接近1，说明自变量对设计要求的影响越大，偏相关系数与相关系数的差别在于不考虑各变量间的相互作用，标准回归系数主要用于评价呈线性关系的自变量与因变量的影响关系，绝对值越大，自变量的改变对因变量的影响越大。结合三种评价结果，从图5 可以看出，前减振器底部衬套刚度kf2 对车身垂向振动影响很小，增大（减小）前、后弹簧连接刚度 kf0、kr0，车身垂向振动相应增大（减小）；增大（减小）前、后减振器连接刚度kf1、kr1，车身垂向振动相应减小（增大）。
衬套刚度的优化
由上述衬套刚度灵敏度的分析结果可知选取适当的衬套刚度，可改善车辆的NVH 性能。此处基于遗传算法，以Kf0、Kf1、Kr0、Kr0 为优化变量，以车身加权加速度均方根值最小为优化目标，由于衬套刚度不仅影响车辆的平顺性，也对车辆的操纵稳定性起着关键的作用，而且一般来说平顺性与操纵稳定性是相互矛盾的，为了在得到较好平顺性的同时保证车辆的操纵稳定性与安全性，以动挠度、动行程、侧倾角与俯仰角满足式（3）作为约束条件，对衬套刚度进行优化。
式中：σfd—悬架动挠度的均方根值；
［fd］—悬架的限位行程，m；
σFd/G—车轮相对动载（动载与静载之比）的均方根值；
φ—车身俯仰角，deg；
φ—车身侧倾角，deg。
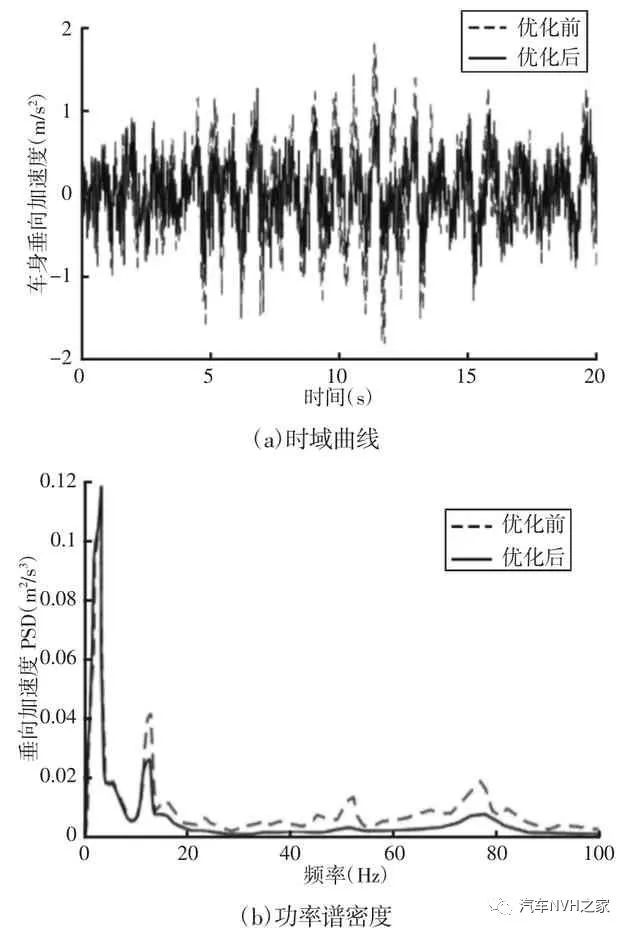
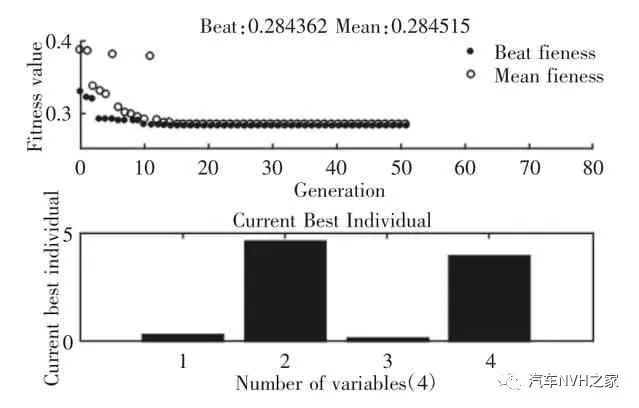
优化变量的上下限分别设置为原衬套刚度的0.2 倍5 倍，通过外惩罚函数将以上不等式约束求解变为无约束求解，收敛精度设置为1e-03，迭代次数设置为80 次，实际迭代51 次达到精度而停止，基于遗传算法的优化迭代过程，如图6 所示。根据以上优化结果计算优化后的车身垂向振动，优化前后的车身垂向振动的时频响应曲线，如图7 所示。图7 显示优化后的减振器垂向振动相比优化前的明显降低了，说明衬套刚度的优化可有效改善车辆的NVH 性能。
图6 衬套刚度优化迭代过程
图7 优化前后车身垂向加速度
结论
针对当前整车振动模型研究的不足之处，建立了综合考虑减振器支柱总成各衬套的整车振动模型，通过理论与仿真相结合的方式，就衬套对整车NVH 的影响进行了一定的研究，取得了以下成果：
（1）根据所研车型建立了含减振器支柱总成各连接衬套的整车振动理论数学模型，并基于随机路面激励模型进行了整车振动模型的求解分析。
（2）通过ADAMS/CAR 的虚拟样机仿真验证了理论模型的正确性，理论与仿真结果均表明减振器支柱总成各衬套可有效改善整车的NVH 性能。
（3）基于Simulink 灵敏度分析的方法研究了各衬套刚度对车辆平顺性的影响，并基于此对衬套刚度进行了优化设计，结果表明，适当选取衬套刚度可以进一步有效改善整车的NVH 性能，研究结果可以为整车性能的优化设计提供一定的参考。
本文作者徐劲力，郭园园，褚金丽，著作权归作者所有，文中观点仅代表作者观点。
广告 
广告
最新资讯
-
《rFpro汽车仿真测试应用系列：智能大灯测
2024-12-04 15:38
-
2025年HBK线下培训课程计划
2024-12-04 11:46
-
欧盟委员会拨款46亿欧元，推动净零技术、电
2024-12-04 11:45
-
曼恩能源解决方案，全尺寸二冲程氨发动机开
2024-12-04 11:44
-
大众汽车“主动弹出式引擎盖”技术
2024-12-04 11:42
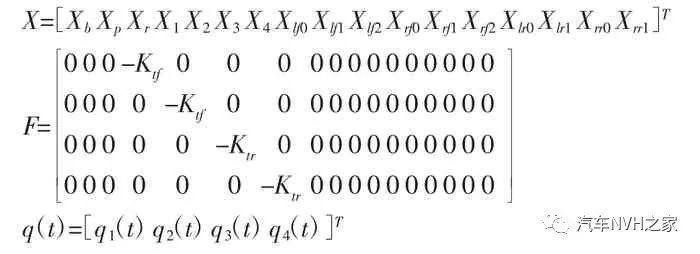
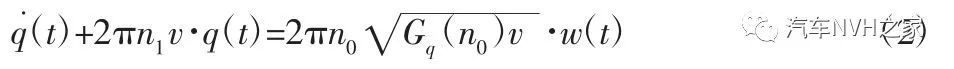
广告
广告
