机器学习最全知识点汇总
主成分分析
线性判别分析
流形学习中的拉普拉斯特征映射
隐马尔科夫模型
5.凸优化
数值优化算法面临两个方面的问题:局部极值,鞍点。前者是梯度为0的点,也是极值点,但不是全局极小值;后者连局部极值都不是,在鞍点处Hessian矩阵不定,即既非正定,也非负定。
凸优化通过对目标函数,优化变量的可行域进行限定,可以保证不会遇到上面两个问题。凸优化是一类特殊的优化问题,它要求:
优化变量的可行域是一个凸集
目标函数是一个凸函数
凸优化最好的一个性质是:所有局部最优解一定是全局最优解。机器学习中典型的凸优化问题有:
线性回归
岭回归
LASSO回归
Logistic回归
支持向量机
Softamx回归
6.拉格朗日对偶
对偶是最优化方法里的一种方法,它将一个最优化问题转换成另外一个问题,二者是等价的。拉格朗日对偶是其中的典型例子。对于如下带等式约束和不等式约束的优化问题:
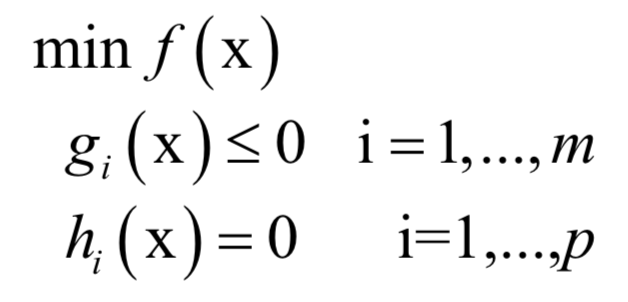
与拉格朗日乘数法类似,构造广义拉格朗日函数:
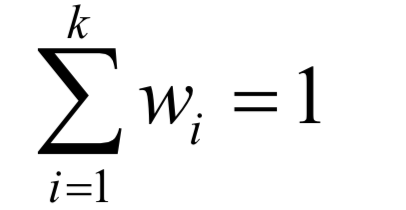
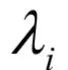
必须满足
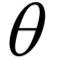
的约束。原问题为:
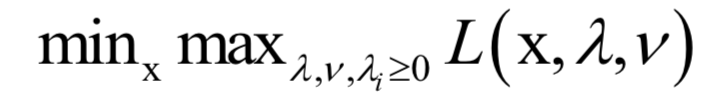
即先固定住x,调整拉格朗日乘子变量,让函数L取极大值;然后控制变量x,让目标函数取极小值。原问题与我们要优化的原始问题是等价的。
对偶问题为:
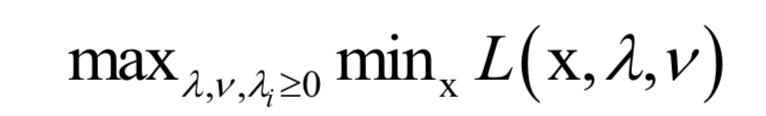
和原问题相反,这里是先控制变量x,让函数L取极小值;然后控制拉格朗日乘子变量,让函数取极大值。
一般情况下,原问题的最优解大于等于对偶问题的最优解,这称为弱对偶。在某些情况下,原问题的最优解和对偶问题的最优解相等,这称为强对偶。
强对偶成立的一种条件是Slater条件:一个凸优化问题如果存在一个候选x使得所有不等式约束都是严格满足的,即对于所有的i都有gi (x)<0,不等式不取等号,则强对偶成立,原问题与对偶问题等价。注意,Slater条件是强对偶成立的充分条件而非必要条件。
拉格朗日对偶在机器学习中的典型应用是支持向量机。
7.KKT条件
KKT条件是拉格朗日乘数法的推广,用于求解既带有等式约束,又带有不等式约束的函数极值。对于如下优化问题:
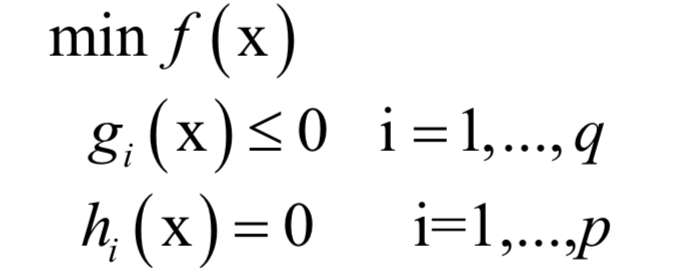
和拉格朗日对偶的做法类似,KKT条件构如下乘子函数:
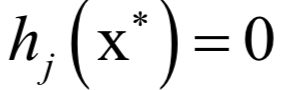
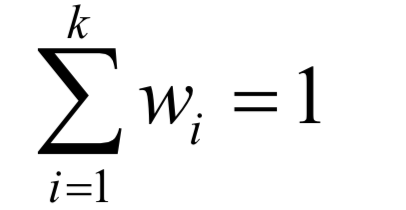
和
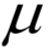
称为KKT乘子。在最优解处
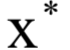
应该满足如下条件:
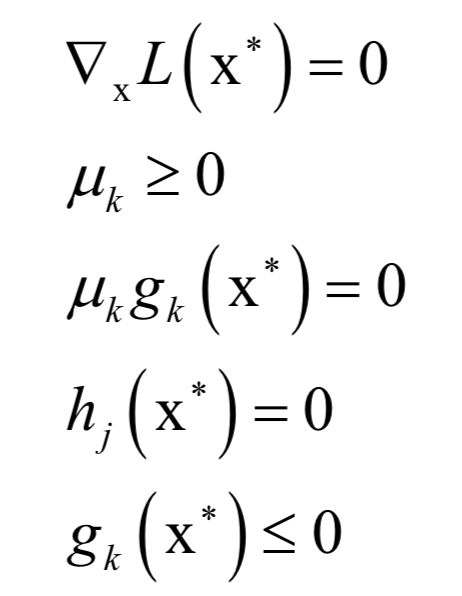
等式约束
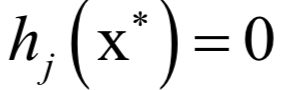
和不等式约束
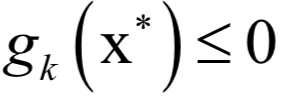
是本身应该满足的约束,
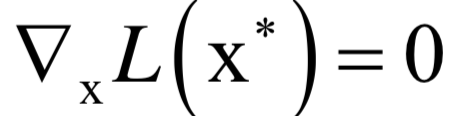
和之前的拉格朗日乘数法一样。唯一多了关于gi (x)的条件:
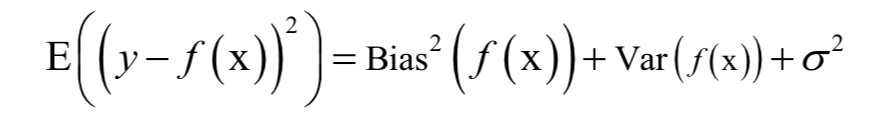
KKT条件只是取得极值的必要条件而不是充分条件。
8.特征值与特征向量
对于一个n阶矩阵A,如果存在一个数
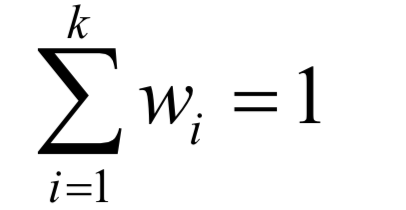
和一个非0向量X,满足:
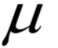
则称
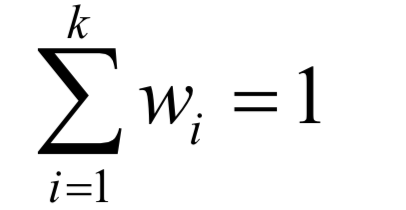
为矩阵A的特征值,X为该特征值对应的特征向量。根据上面的定义有下面线性方程组成立:
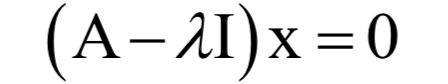
上式左边的多项式称为矩阵的特征多项式。矩阵的迹定义为主对角线元素之和:
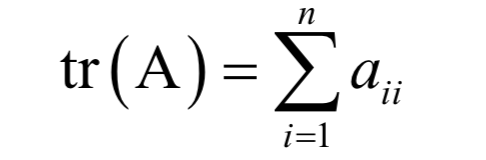
根据韦达定理,矩阵所有特征值的和为矩阵的迹:
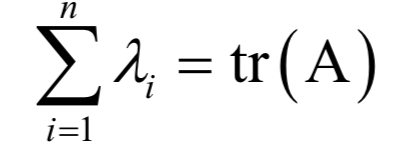
同样可以证明,矩阵所有特征值的积为矩阵的行列式:
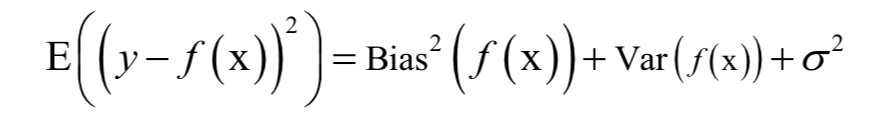
利用特征值和特征向量,可以将矩阵对角化,即用正交变换将矩阵化为对角阵。实对称矩阵一定可以对角化,半正定矩阵的特征值都大于等于0,在机器学习中,很多矩阵都满足这些条件。特征值和特征向量在机器学习中的应用包括:正态贝叶斯分类器、主成分分析,流形学习,线性判别分析,谱聚类等。
9.奇异值分解
矩阵对角化只适用于方阵,如果不是方阵也可以进行类似的分解,这就是奇异值分解,简称SVD。假设A是一个m x n的矩阵,则存在如下分解:
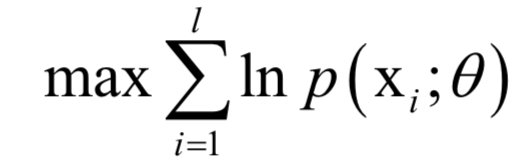
其中U为m x m的正交矩阵,其列称为矩阵A的左奇异向量;
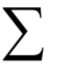
为m x n的对角矩阵,除了主对角线
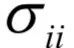
以外,其他元素都是0;V为n x n的正交矩阵,其行称为矩阵A的右奇异向量。U的列为AAT的特征向量,V的列为AT A的特征向量。
10.最大似然估计
- 下一篇:新能源乘用车产业现状及发展趋势
- 上一篇:量产主控芯片的网络安全设计
编辑推荐
最新资讯
-
中汽中心工程院能量流测试设备上线全新专家
2025-04-03 08:46
-
上新|AutoHawk Extreme 横空出世-新一代实
2025-04-03 08:42
-
「智能座椅」东风日产N7为何敢称“百万级大
2025-04-03 08:31
-
基于加速度计补偿的俯仰角和路面坡度角估计
2025-04-03 08:30
-
《北京市自动驾驶汽车条例》正式实施 L3级
2025-04-02 20:23





 广告
广告





























































