汽车结构疲劳分析基础——材料S-N曲线的构建

01、概述

从19世纪中叶开始，工程界开始引入疲劳的概念，当时的分析和设计都是以应力为基础，这种方法称为应力法。应力法一般用于高周疲劳工况，疲劳失效时的循环次数高，加载过程中材料不发生屈服或者只出现很小的塑性应变。

应力法将循环应力作为疲劳失效的控制参数。进行疲劳寿命计算时必须输入反映材料抗疲劳性能的强度-寿命曲线，这种曲线以达到失效时的加载循环数目N为横坐标，以应力幅值S为纵坐标，叫做应力-寿命，即S-N曲线。

材料S-N曲线的测试，至今仍然沿用Wohler在19世纪50年代提出试验方案，即将一定特征的恒定幅值应力循环施加到特定试样，根据试验结果绘制出曲线。

在试验测试时，我们不可能真正加载无限长时间，也不可能测试无限多个试样。实际测试时必须遵守一定的限制条件和规则，才可能通过少量试样和有限加载次数来得到满足工程精度的S-N曲线。

02、高周疲劳试验试样和设备

材料S-N曲线表达的是名义应力S和加载次数N之间的关系，使用何种应力取决于加载方式。常见的加载方式有弯曲、轴向和扭转三种，分别对应旋转弯曲试验、拉压试验和扭转试验。

可使用传统的弹性力学公式将试验载荷与应力联系起来，如下：

①旋转弯曲疲劳试验—弯曲S-N曲线：  

②拉压疲劳试验—拉压S-N曲线：  

③扭转疲劳试验—扭转S-N曲线：  

2.1 试样的制备

材料S-N曲线通过高周疲劳试验测定，通常使用结构简单、造价低廉的标准试样。不同加载方式需采用不同形状的试样。

常规测试使用光滑试样；为了研究缺口敏感度会采用缺口式样；研究焊点焊缝的S-N曲线时，需要使用专门的焊接接头试样。如图1所示。

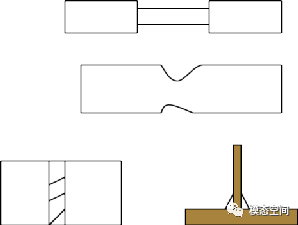
图1 光滑试样、缺口试样与焊接接头试样

旋转弯曲试样

旋转弯曲标准试样为圆形截面试样，国标GB/T4337-2015中推荐了其形状，如图2。推荐尺寸见表格1。

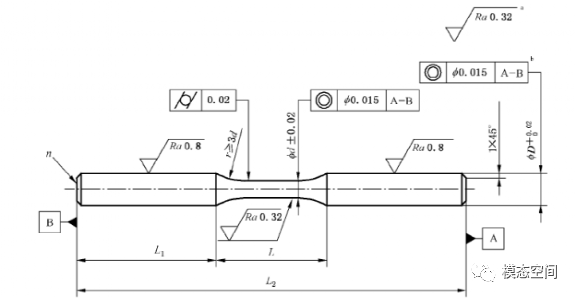
图2 弯曲加载试样的形状

表格1 弯曲加载试样的推荐尺寸

标距段直径d

d的公差

圆角r

长度L

6mm/7.5mm/9mm

 ±0.02mm

 ≥3d

40mm

 ≥1.5

轴向加载试样

轴向加载试样理论上对于横截面形状和标距长度没有限制，只要满足以下几个条件：

1. 提供均匀的标距部分

2. 减少压缩时的屈曲风险，避免在过渡半径处发生失效。

3. 整个标距段提供均匀的应力或者应变分布。

国标GB/T3075-2020中推荐了轴向加载圆形或矩形截面标准试样的形状，如图3和图4。

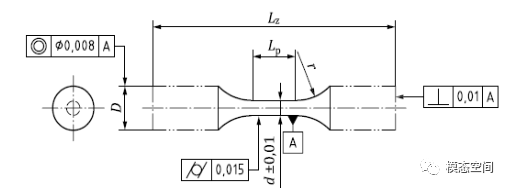
图3 轴向加载圆形截面试样

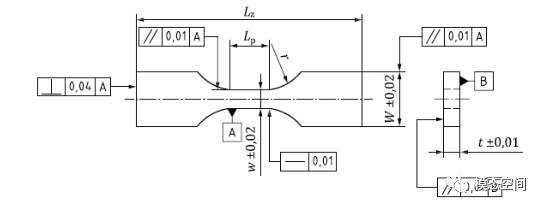
图4 轴向加载矩形截面试样

对于轴向加载，应尽量使用圆形截面试样，因为矩形试样难以获得较小的表面粗糙度，而且在矩形横截面的拐角容易提前萌生疲劳裂纹。

圆形截面轴向加载试样的尺寸定义如表格2。如果轴向加载仅有拉伸载荷，长度L建议尽量大一些。如果轴向加载包含压缩载荷，为避免发生压缩失稳，应使L<4d。

表格2 轴向加载试样的推荐尺寸

参数
尺寸
圆柱形测量部分的直径
5mm≤d≤10mm平行长度
Lp≥2d过渡弧（从平行部分到夹持端）
r≥2d外部直径（夹持端）
D≥2d减缩部分长度
Lz≤8d

扭转加载试样

扭转加载疲劳试样通常采用与旋转弯曲试样类似的形状，只是试样夹持部分需加工出防止加载时试样滑动的平台，如图5。

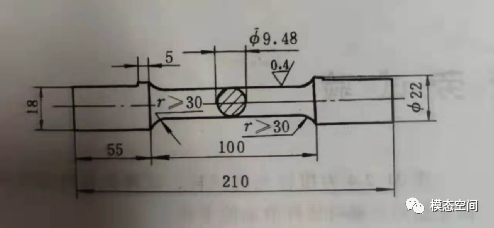
图5 扭转加载试样

漏斗形试样

高应力高加载频率的弯曲和轴向疲劳试验都可能引起试样在试验过程中过热，此时可考虑采用漏斗形的试样，如图6。

漏斗形试样的特点是夹持端与圆形试样的最小直径处（或者矩形截面试样的最小宽度处）有一个连续的半径，它没有一个均匀的标距段，在最小横截面上的应力分布并不是完全均匀的，所以它的S-N曲线与常规试样得到的曲线会有一定差异。

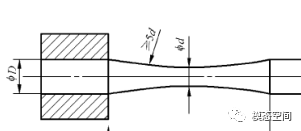
图 6 漏斗形试样

2.2 高周疲劳测试设备

旋转弯曲疲劳试验机

试样受铅垂力作用而承受纯弯矩，当电机驱动试样高速旋转时，试样上的应力值发生拉压对称交变，使材料承受对称应力。这种方法由Wohler在19世纪50年代提出，因为具有设备低廉、操作简单、测试时间短的优点，至今仍在广泛应用，一般只用于弯曲S-N曲线的测定。

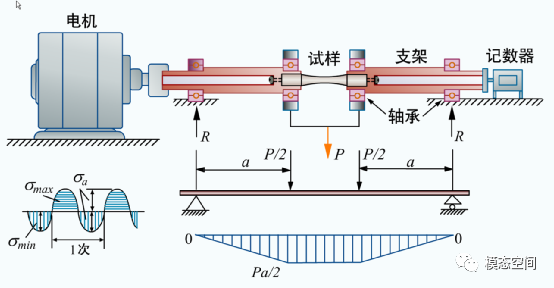
图7 弯曲疲劳试验机原理示意

电磁谐振式高频疲劳实验机

谐振式高频疲劳试验机靠共振特性对试样加力，应力交变频率高，能够在短时间内实现多次加载循环，对于减少测试时间相当有效。可进行拉压疲劳、弯曲疲劳、扭转疲劳试验，对称循环与非对称循环均可实现。因其共振工作特性，不能进行橡胶、塑料等非线性材料的疲劳试验；也不能进行进入塑性范围的金属疲劳实验。

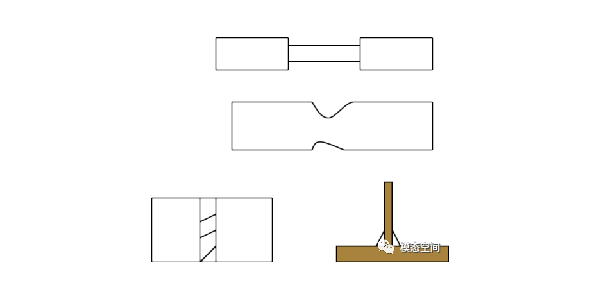
图8 电磁谐振式高频试验机

电液伺服疲劳试验机。

电液伺服疲劳试验机可以实现精确、连续的压力控制，可精确地控制输出最小试验负荷和最大试验负荷。不仅能瞬时输出尖端脉冲，而且可以由计算机控制其输出正弦波、三角波或方波，不但可以做动态疲劳试验，还可以做试件的静态性能试验。

图9 电液伺服疲劳试验机

03、材料SN曲线的测试方法

测试S-N曲线的高周疲劳试验方案，通常有常规试验法、成组试验法和升降法三种。

3.1 常规试验法

常规试验法一般需制备十个以上的相同的试样，一个用于测定静载强度，7-8个用于疲劳试验，剩下的1-2个做备用。

试验中根据静载强度  对试验应力幅值进行分级，至少分为7级。高应力水平低的间隔可以大些，低应力水平的间隔要相应减小。最高应力水平可先尝试使用0.6-0.7  。

确定疲劳极限时，要求至少有两个试样达到循环基数而不发生失效，这样才能保证疲劳极限结果的可靠度。

得到各级应力水平下的循环次数和疲劳极限后，在图上绘制出数据点，进而得到S-N曲线。

3.2 成组试验法

试件的疲劳寿命实际有相当大的离散性，常规试验法在每个应力水平下只测一个试样，这样得到的S-N曲线精度很差。对于汽车结构的耐久可靠性设计，我们要考虑疲劳寿命的概率分布，需要给出P-S-N曲线，即指定存活率下的S-N曲线。此时在有限寿命段需要进行成组试验法，也就是在每个应力水平上使用一组试样来试验。

为了保证足够精度，每组试样数目不应小于6。增大试样数目有利于提升精度，但实践证明每组试样数目超过14时，精度的提升已不明显。所以通常建议每组试样为6-10个，高应力水平组采用6个试样，低应力水平组可增加到10个。

根据成组测试结果，可以得到指定存活率P下每级应力水平  所对应的疲劳寿命  ，从而得到曲线图上的一个数据点  。

将各数据点数据点顺序连接即为指定存活率下的S-N曲线。实际绘制曲线时一般不会逐点直接连接，而是建立一条光滑的曲线，让曲线两侧的数据点与曲线的偏离大致相等，如图10；或者是假定S-N曲线在双对数坐标下为直线段，采用最小二乘法确定出最佳的拟合直线。

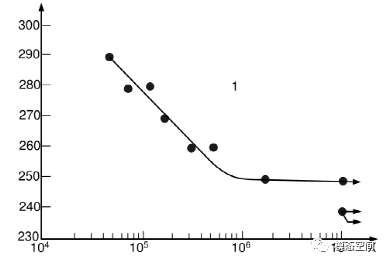
图10 根据数据点绘制光滑曲线

3.3 升降法试验

升降法主要用于长寿命区，可以比较精确地得到疲劳极限。在指定寿命  下（对于钢材可取10E7），预估该寿命对应的疲劳极限，第一个试样采用高于疲劳极限的应力水平进行加载。如果第一个试样在未达到  时发生破坏，下一个试样的试验就在低一级的应力水平下进行。如果试样在当前应力水平下达到  次循环仍未破坏，即发生越出，则下一个试样就在高一级应力水平下进行，如图11。

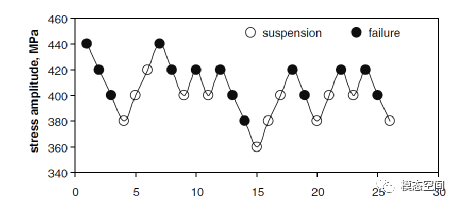
图11

升降法求疲劳极限

把所有临近出现相反结果（即一个越出一个破坏）的数据点配成对，共n个数据对，每对应力求平均值，得到的n个平均值再求出均值，就可以作为疲劳极限的精确值。

如图12所示，金属在双对数坐标下的S-N曲线可分为两类，一类有水平线，如合金钢，由斜线到水平线拐点的应力值即为疲劳极限。一类无水平线， 没有拐点，如灰铸铁，理论上只能定义条件寿命下的疲劳强度，即条件疲劳极限。无论是疲劳极限还是条件疲劳极限，采用升降法都能得到比较精确的结果。

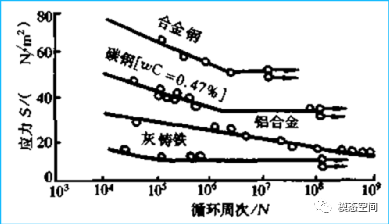
图12 带拐点和不带拐点的S-N曲线

升降法测定的疲劳极限或者条件疲劳极限，与成组试验法测定的寿命数据合并后，就得到了涵盖有限寿命区和无限寿命区的P-S-N曲线。

3.4 小样本中值S-N曲线测试

如果我们只要求得到P-S-N曲线的中值，即存活率50%的S-N曲线，成组试验的每组试样数可以减少到3-5个。

文献中记载了一种中值S-N曲线测试法，每组试样数进一步减少到2个，有限寿命段仅有四种应力水平，这样在有限寿命区域仅需要8个试样。该方法仍采用升降法确定疲劳极限，需要再使用6个试样。这样测定一条完整的中值S-N曲线一共只需要14个试样。该方法假定有限寿命段在双对数坐标中为线性，采用最小二乘法拟合，如图13。

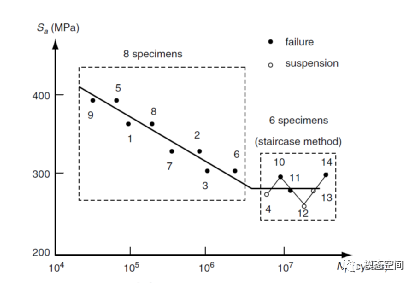
图13 小样本中值S-N曲线测试方案

04、材料疲劳极限和SN曲线的估算方法

测定某种材料的S-N曲线和疲劳极限需要多个试样，需要进行上千万次的加载，时间和费用消耗极大。而汽车结构涉及上百种材料，通常很难对每种材料都进行高周疲劳测试。因此研究人员发展了一些简单的方法，根据材料硬度、延伸率、拉伸极限等常见参数来估计疲劳极限和S-N曲线。

材料疲劳极限的估算

可以根据极限强度  近似估计对称加载（R=-1）时的疲劳极限  。一般情况下，极限强度  取为材料拉伸极限   ；也有文献认为对于脆性材料取拉伸极限，对于韧性材料则应取屈服极限。本文更倾向于对于脆性和韧性材料都使用拉伸极限

对于旋转弯曲： 

在疲劳仿真分析中，我们最常用的是轴向加载的疲劳极限，对于轴向拉压工况， 

试验数据表明，大部分常规钢材的拉压疲劳极限在0.3-0.45   之间，印证了上式的的合理性。

扭转载荷作用下的疲劳极限可估计为： 

试验数据表明，大部分常规钢材的扭转疲劳极限在0.25-0.3  之间。

无试验数据时S-N曲线的估计

假定1：寿命 N=1000时，有 

弯曲工况拉压工况扭转工况假定2：寿命N=1E6时，有  ，其中  用式(1)(2)(3)来确定。这样就确定了S-N曲线的两个点  和(  )。将双对数形式的S-N曲线简化考虑为斜线+水平线形式，第二个点即为拐点，第一点和第二点的连线即为斜线段，如图14。

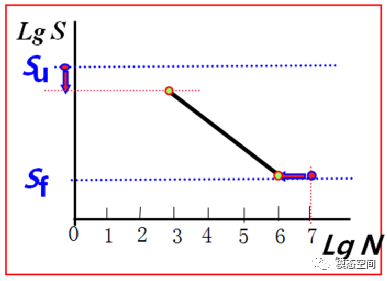
图14  材料S-N曲线的估算方法

作者简介

王朋波，清华大学力学博士，汽车结构CAE分析专家。重庆市科协成员、《计算机辅助工程》期刊审稿人、交通运输部项目评审专家。专业领域为整车疲劳耐久/NVH/碰撞安全性能开发与仿真计算，车体结构优化与轻量化，CAE分析流程自动化等。