广告
换道避障时的路径规划
车道变换是车辆从一个车道变换到另一个车道的行为，是车辆运动过程中最常见的运动之一。当自由换道时，可以根据边界条件通过求解横向和纵向五次多项式确定换道轨迹；当换道过程中遇到障碍物时，还需要考虑换道过程中可能出现的碰撞问题以及相应的碰撞检测，本文以完全符合车辆形状的矩形对换道车辆和障碍物车辆包裹进行碰撞检测，并根据起始与终止状态的边界条件及运动学限制最终得到合理的换道轨迹。
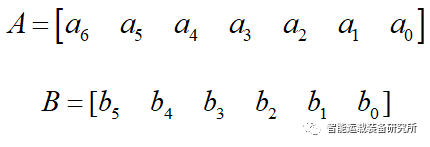
图1 单障碍物情况下车辆换道
图1描述的超车行为中，C0为换道车辆，O1为车道中存在的障碍车辆，C0由初始车道经过时间t变换到目标车道，完成对障碍车辆O1的超越，同时保证在整个过程中与O1不发生碰撞。这种情况下需要增加换道轨迹的约束条件。考虑车辆在实际换道过程中纵向速度的变化范围要比横向速度大得多，其调整的自由度更大，因此，通常通过增加纵向多项式的次数来实现避撞，车辆的横纵向轨迹方程可以表示为：
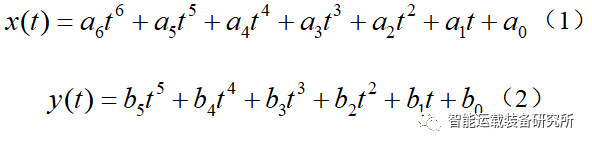
求换道轨迹即求取轨迹方程中的系数矩阵
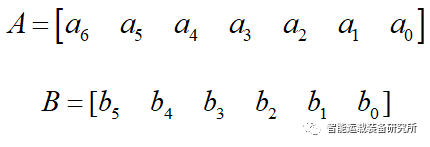
对x(t)和y(t)分别求一阶和二阶导数，就可以得到纵向、横向速度和加速度方程。
速度方程：
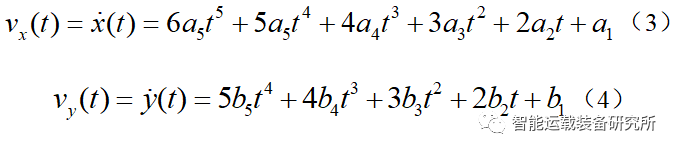
加速度方程：
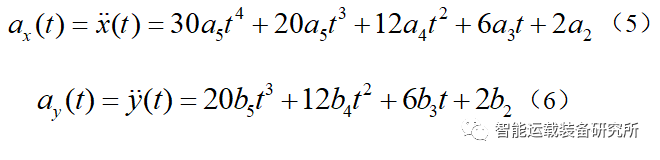
假设车辆换道的初始状态和目标状态分别为：
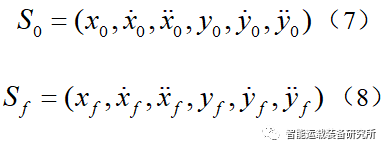
则可得
整理可得
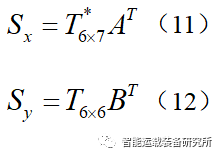
在对换道的初始状态和目标状态进行赋值时通常做如下假设：在换道过程中目标车辆与道路方向夹角为0，即换道过程中车辆呈平动状态。在实际换道过程中，车辆运行方向与道路方向的夹角不为0，即车辆的偏航角不为0，否则无法完成换道行为，但考虑到该偏航角较小，同时换道行为车辆产生的纵向位移远大于横向位移，因此忽略换道车辆运动过程中的偏航角这一假设是合理的。将换道车辆与障碍物进行矩形包裹，如下图所示。
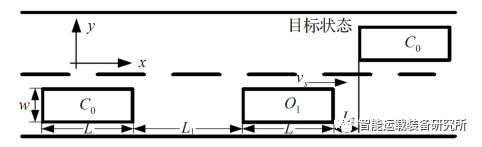
图2 车辆换道矩形表示
C0车与O1车的长、宽相同，分别为L与W，在换道初始时刻t=t0时C0落后O1距离L1，当换道结束t=tf时C0超越O1，在整个运动过程中O1以速度Vs匀速直线行驶。定义delta=tf-t0，即在delta时间段内换道车辆完成了超车、换道操作。
首先式（12）可以根据边界条件求出矩阵系数B，得到横向换道轨迹函数；假设在t=tc时刻C0的车头到达O1车尾位置，如下图所示，称tc为碰撞时间。
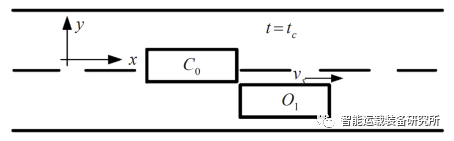
图3 到达碰撞点时t=tc两车的位置
换道轨迹函数y(t)为单调递增函数，因此结合假设可以得到结论：当y(tc)>W时，C0与O1不会相撞。
结论的意义为：若两车在换道过程中不发生碰撞，那么在碰撞时刻t=tc换道车辆C0已经向目标车道方向至少产生一个整车宽度W的位移，等号成立的情况为临界碰撞状态。在图3所示的换道过程中，对C0车的下边缘与前边缘和O1车的后边缘与上边缘做碰撞检测，由此可得到x方向参数矩阵A中a6的参数族。得到了a6值外加边界条件便可以求得x方向参数矩阵，这样就将寻求换道轨迹问题转化为寻找一个合适的a6值的问题。
采用以上提出的轨迹规划算法可以快速地获得换道轨迹，但此时得到的换道轨迹并没有考虑其受车辆动力学特性的约束，车辆在实际运动过程中产生的纵向及横向加速度受到发动机、轮胎、地面摩擦力等多方面限制，同时为了保证换道过程中乘坐的舒适性也要对换道过程产生的最大纵向及侧向加速度进行约束，取换道产生的纵向及横向加速度应满足：
式（13）、（14）定义了换道轨迹的舒适性范围，即生成的路径轨迹性能参数不应超出此范围。如果计算得到的路径轨迹性能指标超出了该范围，需要调整换道车辆的边界条件以及换道时间delta，重新进行路径规划以使其满足乘坐舒适性要求。一般来说y方向加速度限制容易得到满足，由于y方向系数矩阵B的计算与x方向系数矩阵A相独立，因此若计算得到的换道轨迹不满足式（14），那么仅需要调整参数delta直到满足最大横向加速度限制即可。前面已将复杂路况下的换道轨迹规划问题转化为寻求合适的x方向系数矩阵参数a6的问题，因此这里提到的车辆动力学限制问题同样归结于a6值的选取问题。
广告
广告
编辑推荐
最新资讯
-
厂商要多努力，才能让用户听起来毫不费力？
2024-11-22 17:10
-
TOP30！海克斯康入选2024福布斯中国数字科
2024-11-22 15:25
-
揭秘国产装备制造厂商的成功秘籍：好耐电子
2024-11-22 15:24
-
一文详解安全分析方法STPA：以自动紧急制动
2024-11-22 15:20
-
选对涉氢压力表：守护涉氢场所安全的关键一
2024-11-22 15:19
广告
广告
