基于快速终端滑模的汽车底盘集成控制

摘 要：针对汽车主动前轮转向子系统和直接横摆力矩控制子系统的集成控制问题，基于快速终端滑模控制理论设计一种标定参数少和动态响应速度快的鲁棒集成控制器.首先，基于达朗贝尔原理建立包含车身侧向和横摆运动自由度的汽车动力学模型作为底盘集成控制模型.随后，基于快速终端滑模控制理论分别设计主动前轮转向控制律和直接横摆力矩控制律，并且通过汽车质心侧偏角相平面定义的平滑切换因子建立二者的切换规则，实现主动前轮转向子系统和直接横摆力矩控制子系统的平滑切换控制，并且将主动前轮转向子系统和直接横摆力矩控制子系统的主要工作区域分别控制在轮胎的线性区域和非线性区域.最后，结合车辆动力学仿真软件对所提出的鲁棒集成控制器的可行性和有效性进行验证，结果表明：所提出的底盘集成控制器可以同时兼顾汽车操纵稳定性和乘坐舒适性.

关键词：车辆工程；底盘集成控制；主动前轮转向；直接横摆力矩控制；快速终端滑模控制；平滑切换控制

随着自动驾驶汽车的飞速发展，智能化电动底盘引起了国内外汽车厂商和众多学者的广泛关注.主动前轮转向（Active Front Steering，AFS）子系统和直接横摆力矩控制（Direct Yaw moment Control，DYC）子系统是智能化电动底盘实现汽车侧向稳定控制的关键执行机构，深入研究二者的集成控制问题对于提高自动驾驶汽车的操纵性和稳定性具有重要的意义.

主动前轮转向子系统和直接横摆力矩控制子系统分别通过主动调节前轮侧向力和四个车轮纵向力来提高自动驾驶汽车的操纵性和稳定性，并且轮胎侧向力和纵向力具有较强的非线性和耦合特性，从而使得AFS 子系统和DYC 子系统在协同工作时呈现出较强的非线性和耦合特性.针对这一问题，许多学者采用线性鲁棒控制方法设计AFS 子系统和DYC 子系统的集成控制器.文献[1]将车速信息作为调度参数，建立了线性时变参数底盘集成控制模型，并设计了底盘集成控制器，实现了AFS 子系统和DYC 子系统的协调控制.文献[2]基于线性二自由度汽车动力学模型设计了AFS 子系统和DYC 子系统的自适应集成控制器，并采用轮胎侧偏刚度自适应律抑制线性二自由度汽车动力学模型与实际汽车动力学特性的偏差对集成控制性能的影响.文献[3]将包含参数摄动的汽车线性二自由度动力学模型作为控制模型，并利用鲁棒L2-L∞/H∞混合控制方法设计了AFS 子系统和DYC 子系统的集成控制器.文献[4]将AFS 子系统和DYC 子系统的集成控制问题分解成主环路控制层和从环路分配层，并采用序列二次优化方法重点设计了从环路分配层.文献[5]基于线性分段轮胎模型建立了汽车底盘集成控制模型，并结合线性二次型优化控制方法和模糊逻辑控制方法设计了AFS 子系统和DYC 子系统的多模型集成切换控制器.上述研究成果均以线性二自由度汽车动力学模型为基础构建AFS 子系统和DYC 子系统的集成控制模型，得到的集成控制器结构形式简洁、计算效率高，但是在汽车极限行驶工况下呈现出较大的保守性.

为了提高AFS 子系统和DYC 子系统在汽车极限行驶工况下的集成控制性能，降低其保守性，许多学者采用非线性鲁棒控制方法解决AFS 子系统和DYC 子系统的集成控制问题.文献[6]采用滑模控制方法实现了AFS 子系统和DYC 子系统的集成控制.文献[7]分别基于六自由度汽车动力学模型和十自由度汽车动力学模型独立设计了AFS 子系统和DYC子系统的模型预测集成控制器，仿真对比结果表明：集成控制模型精度越高，所设计的AFS 子系统和DYC 子系统的模型预测集成控制器的性能越好，但是计算效率越低.文献[8]将AFS 子系统和DYC 子系统的集成控制问题转化为状态独立的黎卡提方程的求解问题，由此得到了对模型参数摄动具有强鲁棒性的AFS 子系统和DYC 子系统的集成控制器.文献[9]通过李雅普诺夫稳定性理论推导出了AFS 子系统和DYC 子系统的非线性鲁棒集成控制器，并且在集成控制器中引入参数自适应律，进一步降低了系统的保守性.文献[10]以提高汽车的操纵性和稳定性为控制目标，采用滑模控制方法计算广义校正横摆力矩，并通过模糊逻辑控制方法将广义校正横摆力矩转化为AFS 子系统和DYC 子系统的控制指令.文献[11]基于滑模变结构控制方法设计了AFS 子系统和电液复合制动子系统的集成控制器，并且通过仿真验证了所设计的集成控制器可以有效提高汽车的主动安全性并兼顾制动能量回收.文献[12]基于动态逆控制方法设计了AFS 子系统和DYC 子系统的集成控制器，并采用期望动态模型在线补偿系统的复合干扰，从而消除了系统的复合干扰对集成控制性能的影响.上述研究成果较好地解决了AFS 子系统和DYC 子系统在协同工作时呈现出较强的非线性和耦合特性，并且在汽车极限行驶工况下的保守性更低，但是存在标定参数多、计算效率低等问题.

鉴于此，本文基于快速终端滑模控制理论设计一种具有标定参数少、动态响应速度快和鲁棒性强的AFS 子系统和DYC 子系统的集成控制器.首先，基于达朗贝尔原理建立包含车身横摆和侧向运动自由度的汽车动力学模型作为底盘集成控制模型，并通过线性二自由汽车模型推导出驾驶员期望的横摆角速度和质心侧偏角.随后，基于快速终端滑模控制理论分别设计主动前轮转向控制律和直接横摆力矩控制律，并且通过汽车质心侧偏角相平面定义的平滑切换因子建立主动前轮转向控制律和直接横摆力矩控制律的切换规则，实现AFS 子系统主要工作在轮胎线性区域，DYC 子系统主要工作在轮胎非线性区域，以及平滑切换AFS 子系统和DYC 子系统.最后，结合车辆动力学仿真软件对所提出的AFS 子系统和DYC 子系统的集成控制器的可行性和有效性进行仿真验证.

1 数学模型

1.1 控制模型

简洁、准确的汽车动力学模型是汽车底盘集成控制策略设计的重要基础.如图1 所示，定义固结于地面的坐标系Oxyz 和固结于车身的坐标系Bxyz，基于达朗贝尔原理建立包含车身纵向、横摆和侧向运动自由度的汽车动力学模型[13].

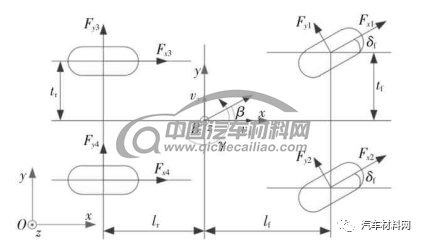
图1 汽车底盘集成控制模型
Fig.1 Integrated vehicle chassis control model

式中：m 和Iz分别为整车质量和汽车绕通过质心的垂直轴的转动惯量；vx、vy和γ 分别为汽车纵向速度、侧向速度和横摆角速度；δf为前轮转向角；Fx1、Fx2、Fx3和Fx4分别为左前、右前、左后和右后轮胎纵向力；lf、lr、tf和tr分别为汽车质心到前轴的距离、汽车质心到后轴的距离、1/2 前轮轮距和1/2 后轮轮距；Fy1和Fy2分别为左前和右前轮胎侧向力；Fyf和Fyr分别为前、后轮胎侧向力的均值，可表示为

式中：Fy3和Fy4分别为左后和右后轮胎侧向力.

汽车侧向和横摆运动是描述其操纵稳定性的核心要素，为了使基于模型设计的汽车底盘集成控制策略简单有效，并且对系统的不确定性具有较强鲁棒性，需要对式（1）描述的汽车动力学模型进一步简化，即：忽略式（1）中描述车身纵向运动自由度动力学方程以及忽略tf（Fy1-Fy2）sin δf项对式（1）中描述车身横摆运动自由度动力学方程的影响，由汽车质心侧偏角的定义β=arctan（vy/vx）≈vy/vx，可将式（1）简化为以汽车质心侧偏角和横摆角速度为状态变量的汽车底盘集成控制模型.

1.2 参考模型

在驾驶员转向操纵过程中，通常认为轮胎侧向力与轮胎侧偏角呈现线性关系是驾驶员期望的汽车响应特性.因此，本文采用线性二自由度汽车模型来描述汽车的期望横摆角速度和质心侧偏角.如图2所示，其动力学方程可以表示为

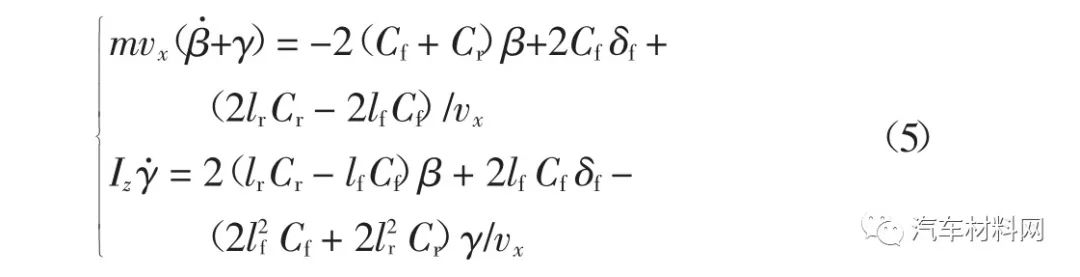
式中：Cf和Cr分别为前、后轮胎等效侧偏刚度.

忽略线性二自由度汽车模型动力学方程的高阶项，将其简化成两个独立的一阶惯性系统，则汽车的期望横摆角速度和质心侧偏角可以表示为

式中：Kγ、Kβ、Tγ和Tβ分别为期望横摆角速度和质心侧偏角的稳态增益和响应时间，可表示为

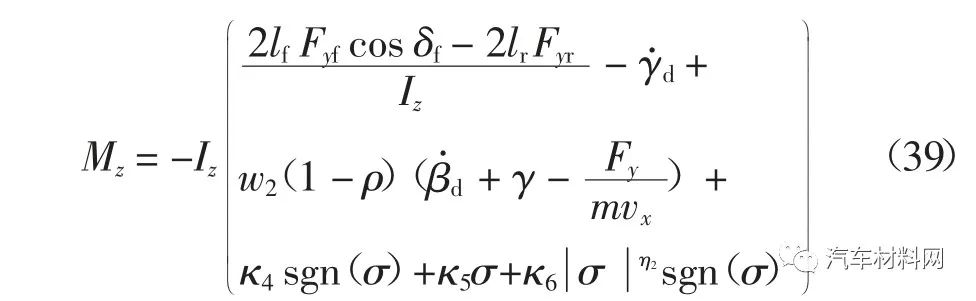
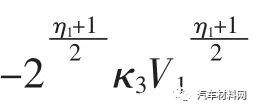
图2 线性二自由度汽车模型
Fig.2 Linear two degree of freedom vehicle model

考虑轮胎-地面附着极限，汽车侧向加速度的绝对值有如下约束[14].

忽略

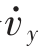
/vx的影响，式（11）可以转化为如下的期望横摆角速度约束.

式中：ζ 为约束修正因子，本文取ζ=0.85.

同时，较大的汽车质心侧偏角容易使驾驶员产生恐慌.因此，期望质心侧偏角的绝对值有如下约束[13].

2 汽车底盘集成控制策略设计

2.1 系统总体架构

汽车底盘集成控制策略总体架构如图3 所示，包括参考模型、主动前轮转向控制律、直接横摆力矩控制律、切换规则和映射模块.主动前轮转向控制律和直接横摆力矩控制律将汽车横摆角速度偏差和质心侧偏角偏差作为输入，分别计算输出校正前轮侧向力增量ΔFAFS和校正横摆力矩增量ΔMDYC.由于AFS 子系统主要工作在轮胎线性区域，而DYC 子系统通常工作在轮胎非线性区域，因此，采用平滑切换因子建立主动前轮转向控制律和直接横摆力矩控制律的切换规则，并且通过切换规则将主动前轮转向控制律和直接横摆力矩控制律的输出修正为

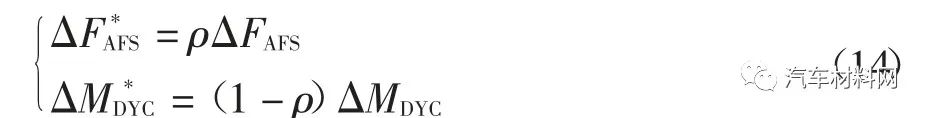
式中：ρ 为平滑切换因子，可表示为

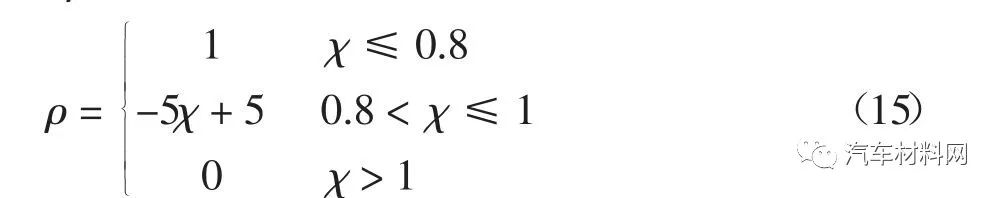
式中：χ 为汽车稳定性因子，可表示为[15]

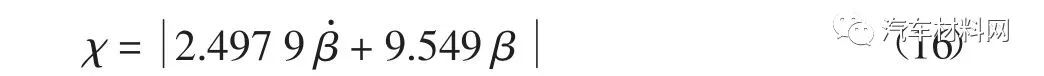
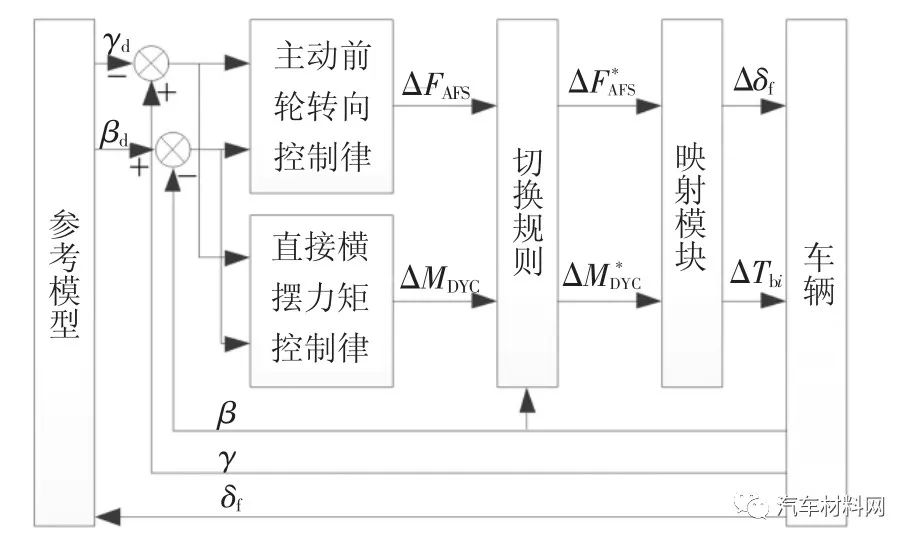
图3 系统总体架构
Fig.3 System overall architecture

由于AFS 子系统主要工作在轮胎线性区域，可以认为轮胎侧向力与轮胎侧偏角之间呈线性关系.因此，修正的校正前轮侧向力增量可以转化为前轮转向角增量[16].

当汽车前轮转向角为正且呈现不足转向，或者汽车前轮转向角为负且呈现过多转向时，修正的校正横摆力矩增量通过制动左前轮和左后轮实现.

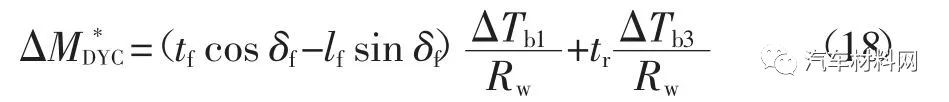
式中：Rw为车轮有效滚动半径；ΔTb1和ΔTb3分别为左前轮和左后轮的制动力矩.

为了充分利用左前轮和左后轮的制动力，建立如下的左前轮和左后轮制动力矩的关系.

式中：μ1和μ3分别为左前轮和左后轮的地面附着系数峰值；Fz1和Fz3分别为左前轮和左后轮的垂向载荷.

将式（19）代入式（18），可得

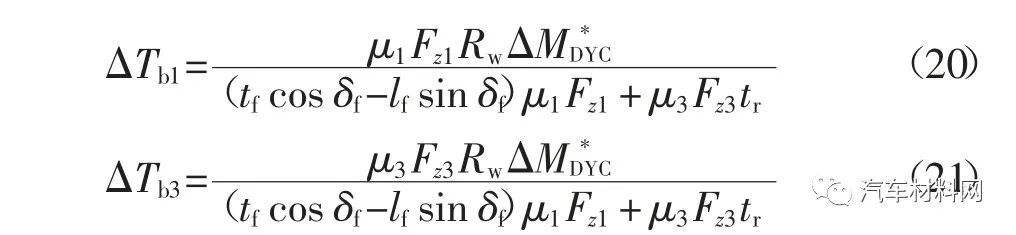
当汽车前轮转向角为正且呈现过多转向，或者汽车前轮转向角为负且呈现不足转向时，修正的校正横摆力矩增量通过制动右前轮和右后轮实现.

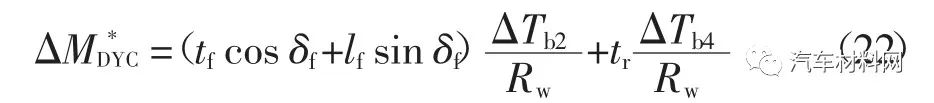
式中：ΔTb2和ΔTb4分别为右前轮和右后轮的制动力矩.

为了充分利用右前轮和右后轮的制动力，建立如下的右前轮和右后轮制动力矩的关系.

式中：μ2和μ4分别为右前轮和右后轮的地面附着系数峰值；Fz2和Fz4分别为右前轮和右后轮的垂向载荷.

将式（23）代入式（22），可得

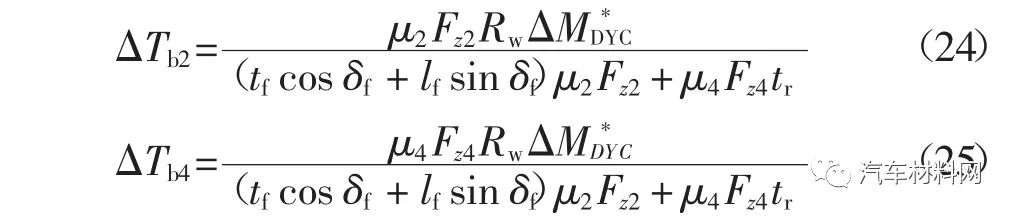
2.2 主动前轮转向控制律设计

AFS 子系统主要工作在轮胎线性区域，通过主动调节前轮侧向力来提高汽车的操纵性.由图1 可知，在式（4）基础上附加校正前轮侧向力增量ΔFAFS可建立如下形式的主动前轮转向控制模型.

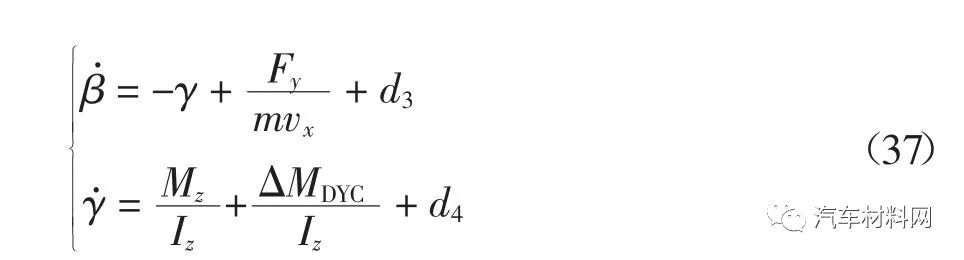
式中：d1和d2分别表示校正前轮侧向力增量对Fy和Mz的加性不确定性，满足

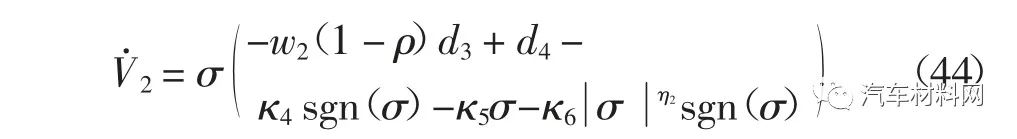
和Mz表示为

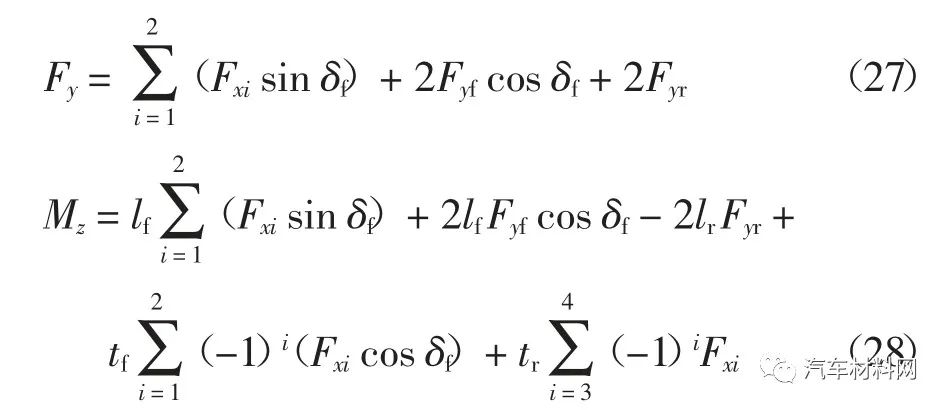
AFS 子系统的控制目标是在汽车稳定行驶前提下，使其横摆角速度快速、稳定的跟踪期望值.因此，定义如下滑模面

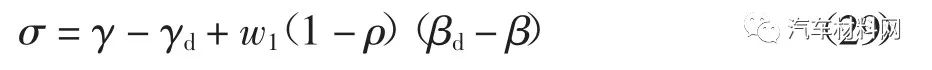
式中：w1为权重系数.

基于式（29）定义的滑模面，采用快速终端滑模控制理论设计主动前轮转向控制律，由此得到定理1.

定理1 考虑式（26）描述的主动前轮转向控制模型，设计如下主动前轮转向控制律

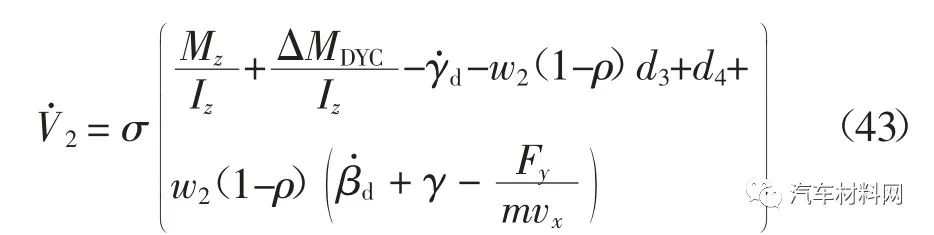
式中：κ1＞0、κ2＞0、κ3＞0 和η1＞1 为主动前轮转向控制律的设计参数.若设计参数κ1满足

则闭环系统的平衡点是渐近稳定的.

证 选取李雅普诺夫候选函数为

对式（32）沿着系统（26）的状态轨迹求导，可得

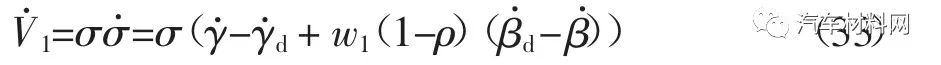
将式（26）代入式（33），可得

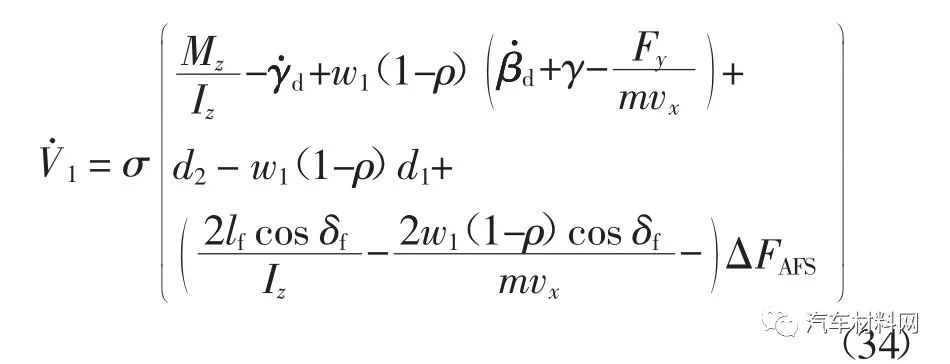
将式（30）描述的主动前轮转向控制律代入式（34），可得

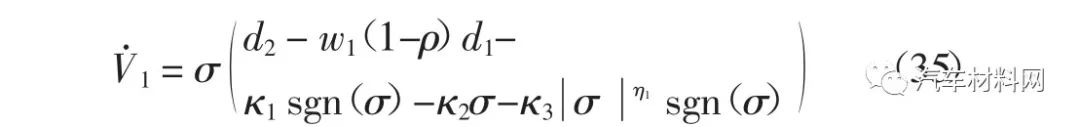
将不等式（31）代入式（35），可得

由不等式（36）可知，当李雅普诺夫候选函数V1＞1 时，不等式（36）右端的第二项

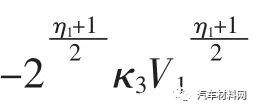
起主导作用，驱动李雅普诺夫候选函数在有限时间内收敛到V1=1，缩短闭环系统状态轨迹的收敛时间；当李雅普诺夫候选函数V1＜1 时，不等式（36）右端的第一项-2κ2V1起主导作用，驱动李雅普诺夫候选函数渐近收敛到零，避免闭环系统的状态轨迹在其平衡点附近产生“振荡”现象.因此，闭环系统的平衡点是渐近稳定的.同时，由上述分析可知，式（30）描述的主动前轮转向控制律包含的设计参数作用明显，便于标定.

2.3 直接横摆力矩控制律设计

DYC 子系统通常工作在轮胎非线性区域，通过主动调节四个车轮纵向力来提高汽车的操纵稳定性.由图1 可知，在式（4）基础上附加校正横摆力矩增量ΔMDYC可建立如下形式的直接横摆力矩控制模型.

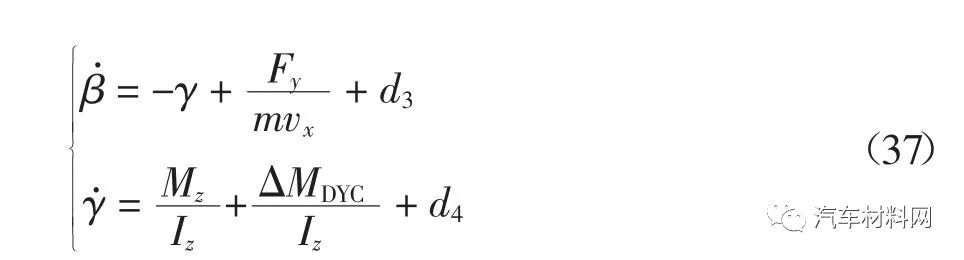
式中：d3和d4分别表示校正横摆力矩增量对Fy和Mz的加性不确定性，满足

DYC 子系统的控制目标是保证汽车稳定的行驶，并且使其横摆角速度快速、稳定的跟踪期望值.因此，定义如下滑模面

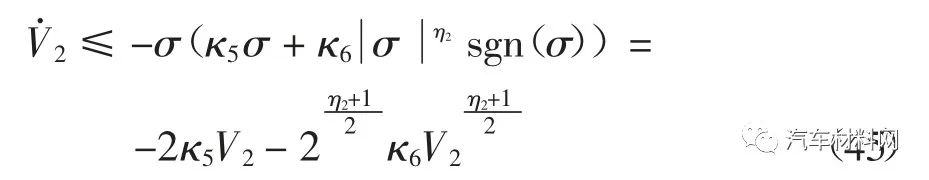
式中：w2为权重系数.

基于式（38）定义的滑模面，采用快速终端滑模控制理论设计直接横摆力矩控制律，由此得到定理2.

定理2 考虑式（37）描述的直接横摆力矩控制模型，设计如下直接横摆力矩控制律

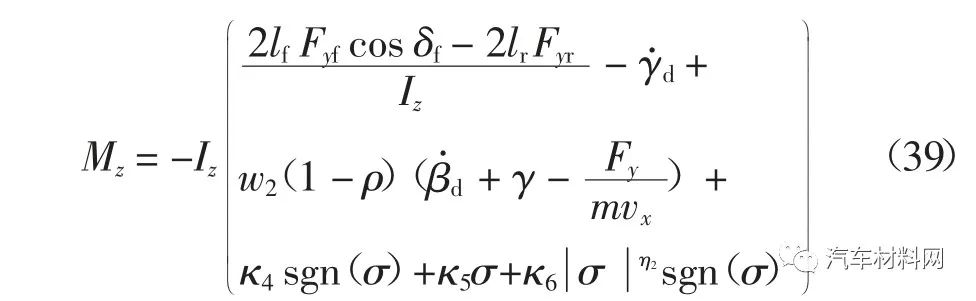
式中，κ4＞0、κ5＞0、κ6＞0 和η2＞1 为直接横摆力矩控制律的设计参数.若设计参数κ4满足

则闭环系统的平衡点是渐近稳定的.

证 选取李雅普诺夫候选函数为

对式（41）沿着系统（37）的状态轨迹求导，可得

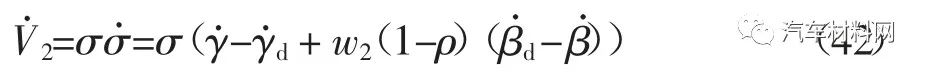
将式（37）代入式（42），可得

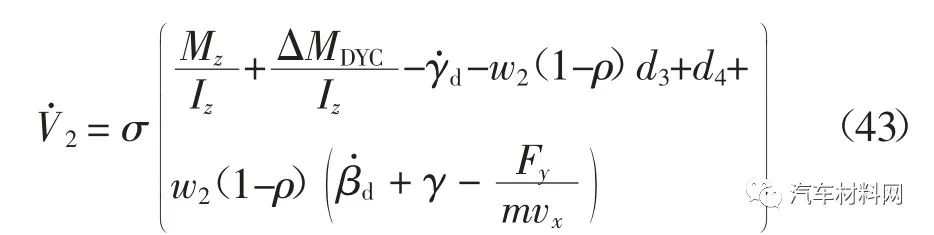
将式（39）描述的直接横摆力矩控制律代入式（43），可得

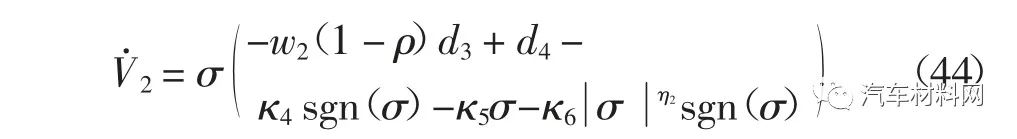
将不等式（40）代入式（44），可得

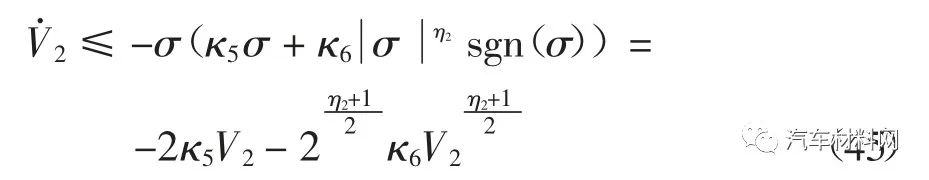
由不等式（45）可知，当李雅普诺夫候选函数V2＞1 时，不等式（45）右端的第二项

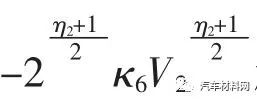
起主导作用，驱动李雅普诺夫候选函数在有限时间内收敛到V2=1，缩短闭环系统状态轨迹的收敛时间；当李雅普诺夫候选函数V2＜1 时，不等式（45）右端的第一项-2κ5V2起主导作用，驱动李雅普诺夫候选函数渐近收敛到零，避免闭环系统的状态轨迹在其平衡点附近产生“振荡”现象.因此，闭环系统的平衡点是渐近稳定的.同时，由上述分析可知，式（39）描述的直接横摆力矩控制律包含的设计参数作用明显，便于标定.

3 仿真结果及分析

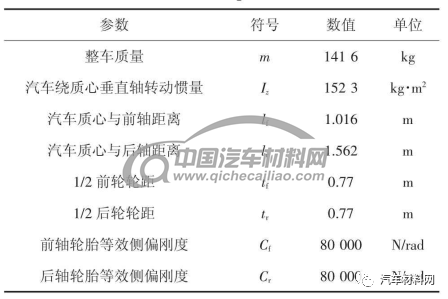
本节采用车辆动力学仿真软件CarSim 对所提出的AFS 子系统和DYC 子系统集成控制器的可行性和有效性进行仿真验证.仿真过程中，集成控制器的参数设置为κ1=20、κ2=300、κ3=100、η1=2.5、w1=0.3、κ4=35、κ5=350、κ6=120、η2=3.5 和w2=2.车辆参数如表1 所示.

表1 车辆参数
Tab.1 Vehicle parameters

3.1 调幅正弦转向工况

在干沥青路面上，将初始车速设置为100 km/h，采用图4（a）所示的前轮转向角作为调幅正弦转向工况的输入，得到的未施加控制、DYC 控制和集成控制的仿真结果如图4（b）-（g）所示.

如图4（b）-（c）所示，汽车期望横摆角速度随着前轮转向角输入增加而增大，DYC 控制和集成控制的汽车均可以快速、稳定地跟踪期望横摆角速度，而未施加控制的汽车呈现不足转向，无法跟踪幅值逐渐增大的期望横摆角速度.如图4（d）-（g）所示，当前轮转向角输入按照正弦信号波动增加时，汽车轮胎在线性工作区与非线性工作区之间切换，使得集成控制的AFS 子系统和DYC 子系统执行切换控制.同时，相对于仅依靠车轮制动力矩来提高汽车操纵稳定性的DYC 控制，集成控制的汽车通过协调AFS 子系统和DYC 子系统来减小对车轮制动力矩的需求，使得集成控制的汽车对纵向速度的影响更小.因此，本文提出的集成控制器可以同时兼顾到汽车操纵稳定性和乘坐舒适性.

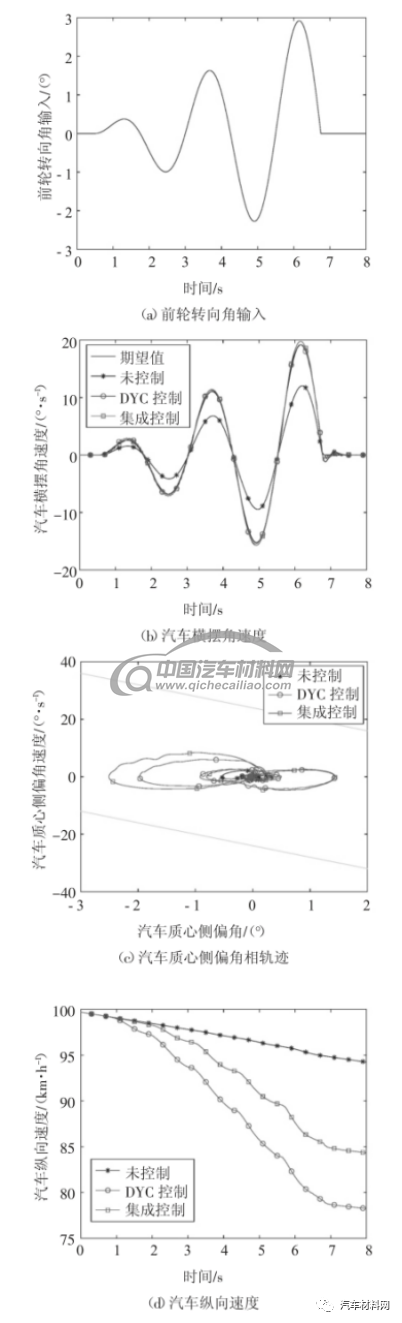
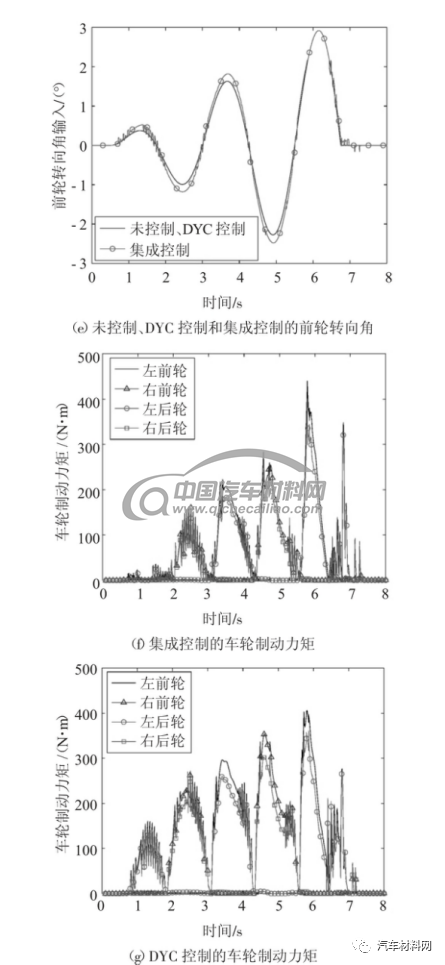
图4 调幅正弦转向工况仿真结果
Fig4 Simulation results of sine with increasing amplitude maneuver

3.2 正弦转向工况

在干沥青路面上，将初始车速设置为120 km/h，采用图5（a）所示的前轮转向角作为正弦转向工况的输入，得到的未施加控制、DYC 控制和集成控制的仿真结果如图5（b）-（g）所示.

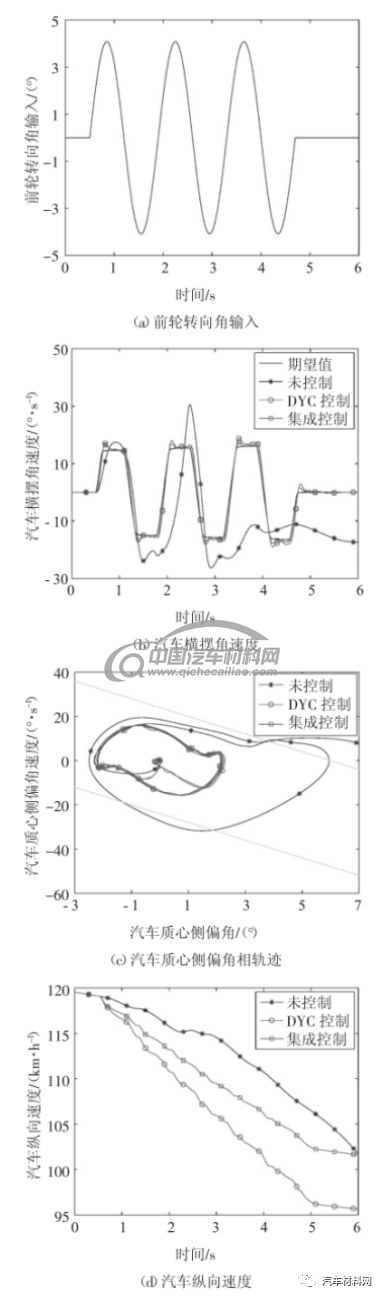
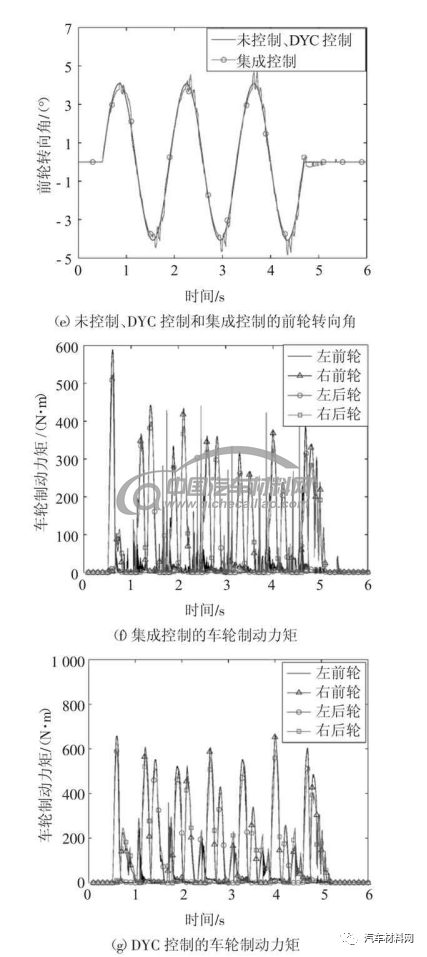
图5 正弦转向工况仿真结果
Fig.5 Simulation results of sine maneuver

如图5（b）-（c）所示，DYC 控制和集成控制的汽车在高速行驶时依然可以准确、稳定的跟踪幅值较大且快速变化的期望横摆角速度，未施加控制的汽车则无法保持稳定行驶而呈现过多转向.同时，相对于DYC 控制的汽车，集成控制的汽车对期望横摆角速度的跟踪精度更高.如图5（d）-（g）所示，相对于仅依靠车轮制动力矩来提高汽车操纵稳定性的DYC控制，集成控制的汽车通过协调AFS 子系统和DYC子系统来减小对车轮制动力矩的需求，使得集成控制的汽车对纵向速度的影响更小.因此，本文提出的集成控制器可以同时兼顾到汽车操纵稳定性和乘坐舒适性.

4 结论

1）基于达朗贝尔原理建立了包含车身侧向和横摆运动自由度的汽车动力学模型作为底盘集成控制模型，并基于快速终端滑模控制理论分别设计了具有标定参数少、动态响应速度快特点的主动前轮转向控制律和直接横摆力矩控制律.

2）通过汽车质心侧偏角相平面定义的平滑切换因子建立了主动前轮转向子系统和直接横摆力矩控制子系统的切换规则，实现了二者的平滑切换控制，并且将二者的主要工作区域分别控制在轮胎的线性区域和非线性区域.

3）采用车辆动力学仿真软件对所提出的汽车主动前轮转向子系统和直接横摆力矩控制子系统的集成控制器的可行性和有效性进行仿真验证，结果表明：所设计的集成控制器可以实现主动前轮转向子系统和直接横摆力矩控制子系统的平滑切换控制，并且可以同时兼顾到汽车操纵稳定性和乘坐舒适性.