简谐载荷下的盘式制动器振动噪声分析及试验

摘 要：以某电动汽车盘式制动器为研究对象，通过CATIA建立制动器三维模型，在Workbench平台上改变制动器的阻尼比，对该模型进行谐响应分析，得到不同阻尼比的制动盘与制动块振幅随频率的分布情况。以制动块消音片为优化目标，用Dynamometer-GIANT 8600惯性实验台分别对无消音片、传统消音片和夹心式消音片的制动器进行振动噪声试验。结果表明：通过改变制动器的阻尼比，能减少制动盘与制动块之间的共振，从而降低振动噪声；夹心式消音片相对于传统的消音片在冷态试验阶段性能表现更好，振动噪声相对传统的消音片降低了约50%。

随着汽车工业4.0的飞速发展与电动汽车的不断普及，人们对车辆各方面的性能提出了更高的要求，其中由车辆制动导致的振动与噪声一直是各大汽车制造商及消费者持续关注并不断改进的问题之一。由于制动的振动与噪声涉及的学科非常广泛，影响因素也很多，国内外学者迟迟找不到一个准确有效的解决措施。

文献[1]分别用求解复模态和时-频域耦合仿真对制动器进行噪声分析，对比指出时-频域耦合法与试验测试结果更为接近，可较为准确地预测制动噪音的频率分布情况。文献[2]利用摩擦学中的随机粗糙面生成法对9组不同的摩擦衬片进行复特征值分析，指出衬片变薄会导致摩擦因数降低，并研究了摩擦衬片的表面特征对制动尖叫的影响情况。文献[3]分析了材料属性、结构参数及制动工况对制动NVH的影响因素，并提出了蒙特卡洛抽样的参数化优化算法，最后通过制动惯量试验台做了相应的验证。文献[4]利用ABAQUS求解了盘式制动器复模态，基于贝叶斯理论推理获得制动啸叫的概率，并通过LMS Virtual.Lab软件对辐射噪声做了仿真分析。

然而由于专业试验设备的欠缺，大多数学者只是停留在软件模拟与小样试验阶段，很少通过专业的试验对其理论进行验证。本文主要以某轿车盘式制动器为研究对象，用CATIA软件建立制动器简化模型，运用Workbench平台对该模型进行谐响应分析，通过改变制动器的阻尼比，得到制动盘与制动块在不同阻尼比的情况下振幅随频率的变化关系；对制动块消音片进行结构改进，用Dynamometer-GIANT 8600惯性实验台以国际通用SAE J2521标准为试验规范对该制动器改进前后模型进行试验分析及验证。

01盘式制动器谐波载荷下的简化模型

汽车盘式制动器制动系统工作时，来自制动主缸的油压通过制动活塞将制动力作用于制动块背板上，两制动块互相挤压制动盘至制动盘停下实现汽车制动[5]。从物理学角度来看，假设在某一时刻下，制动盘相对于制动块向右运动，制动盘旋转的驱动力可转化为向右的牵引力，该牵引力可视为阻尼器和刚度元件[6]。制动块与制动盘之间互相摩擦导致磨屑脱落、挤压引起的不平顺性可通过简谐载荷模型进行模拟。假设制动盘初速度为v0，激励时系统初相位为0，存在系统阻尼，制动块以FN的力压向制动盘，制动盘与制动块之间的摩擦阻力为Ffric，制动器简化模型与物理模型如图1所示。

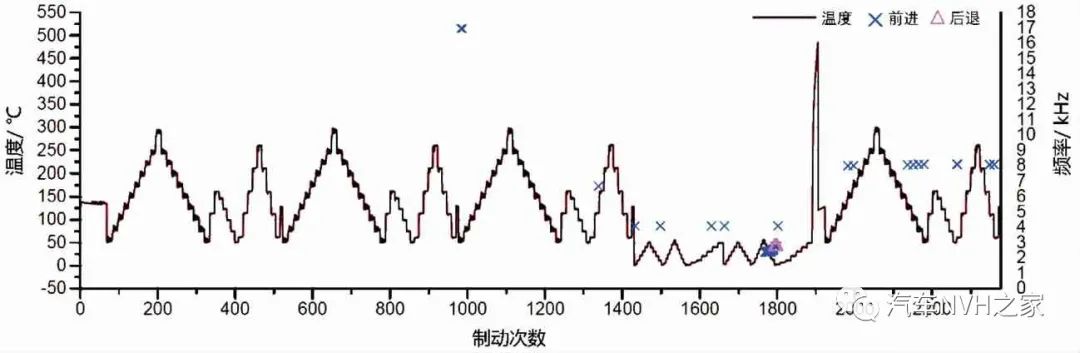
图1 制动器简化模型及其物理模型

假设制动盘质量为m，根据达朗贝尔原理，建立相应的动力学方程[7]

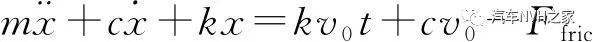
(1)

式中：Ffric为滑动摩擦阻力；c为阻尼系数；k为刚度系数。

假设制动块表面不平度为

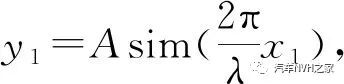
则可通过施加谐波激励进行模拟[8]。令制动块的正压力FN为时间t的周期函数，频率为系统固有频率ω0，F1<<F0，则：

FN=F0+F1cos(ω0t+φ)

(2)

v=v0+v1cosω0t

(3)

式中：F0为理想状态下正压力；F1为简谐载荷下的波动力；v0为理想状态下的初速度；v1为简谐载荷下的波动速度。

由于滑动摩擦因数μ与滑动速度v有关，即μ=μ(v)，因此系统摩擦阻力为

Ffric=FNμ(v)

(4)

假设实测速度与正压力成正比关系，比例系数为ξ，则

FN=ξv

(5)

此时动力学方程为

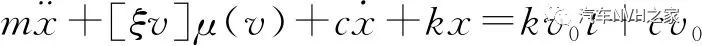
(6)

方程有稳态解：

x=x0+v0t

(7)

线性化方程得：

(8)

为使系统保持稳定状态，阻尼值应为正值，可见系统阻尼的变化将影响系统稳定。

02盘式制动器谐响应分析

2.1 车型相关参数

本文以某电动汽车浮钳盘式制动器为研究对象，目标车型前置前驱，其整车及制动器关键参数如表1所示。

表1 某轿车整车及制动器关键参数

2.2 有限元模型及前处理

基于上述理论分析，以该汽车前制动盘为例，运用三维制图软件CATIA，在不影响分析精度的情况下建立制动器的简化几何模型，并将三维模型文件导入Workbench中进行网格划分。网格划分采用Automatic自动网格划分方式，生成符合质量的模型有限元网格，节点数75 283个，总单元数35 206个。

模型前处理需定义材料和单元类型、接触对与接触条件、载荷与边界条件，最后进行分析及求解控制[9]。简化的制动器主要分3个模块：制动盘、制动块与钢背，其对应的详细材料参数如表2所示。

表2 制动器模型材料参数

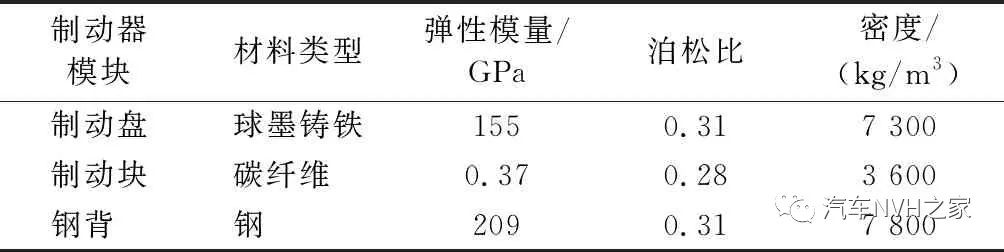
接触对之间采用面与面接触。制动盘与制动块之间的接触面定义为摩擦接触，摩擦因数μ设定为0.35，非对称接触行为。高级选项设置为非线性的收敛并采用增强拉格朗日算法，接触面调整为初始接触，每次迭代更新刚度并设置弹球区域半径R为2 mm。制动块与钢背之间的接触设定为绑定接触，采用对称接触行为并定义为多点约束的Multi-point Constraints(MPC)算法。

本文首先采用非线性静力学进行结构分析，定义载荷与约束，选择两钢背的外表面的圆形区域(活塞压缩区域)，施加0.5 MPa的压力载荷(制动活塞的初始压力)，定义制动块与钢背的表面位移约束：Y和Z轴方向位移为0，X轴方向为自由。然后将分析结果导入Model模块进行模态求解，采用非线性摄动法进行模态分析，用不对称法提取前200阶模态，求解频率范围为0～12 kHz。最后将模态结果导入谐响应分析模块，选定制动盘与制动快的X方向为研究对象，求解各阶频率下相应的振幅。

2.3 不同阻尼比的盘式制动器谐响应分析

制动器振动噪声与频率和幅值大小有着直接的关系[10]。本文通过Workbench谐响应模块分析不同阻尼比的盘式制动器振幅随频率的变化趋势，指出部件在某些频率下发生噪声的可能性，进而对相应的部件做出针对性的改进。

由于金属材料的阻尼比特别低，约在0.001以内，合金材料阻尼比通常在0.05～0.2之间，而粘弹性材料如橡胶，阻尼比可达0.1～5[11]。现在汽车盘式制动器通常采用制动块背板处加贴消音片(即阻尼片)的方式改变系统的阻尼比。本文取阻尼比为0～0.2的范围进行求解分析。对于任何结构方程，阻尼都存在多样性，谐响应模块可在设置中调整部件阻尼比的大小。本文从系统无阻尼开始，对比不同阻尼比(0、0.05、0.1、0.15、0.2)状态下制动盘和制动片的幅值随频率的波动关系，提取得到的不同阻尼比的制动器X轴方向的振幅如图2所示。

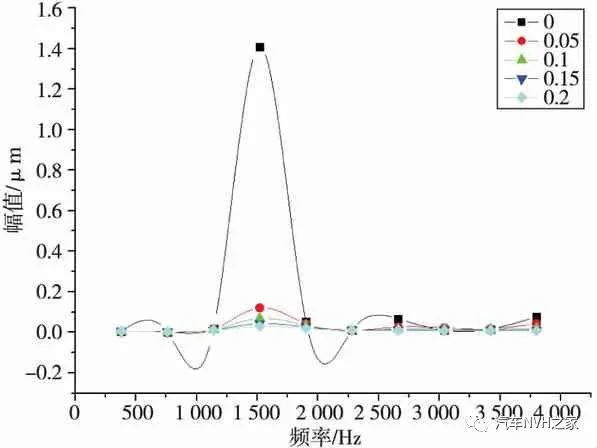
(a) 制动盘振幅随频率波动曲线

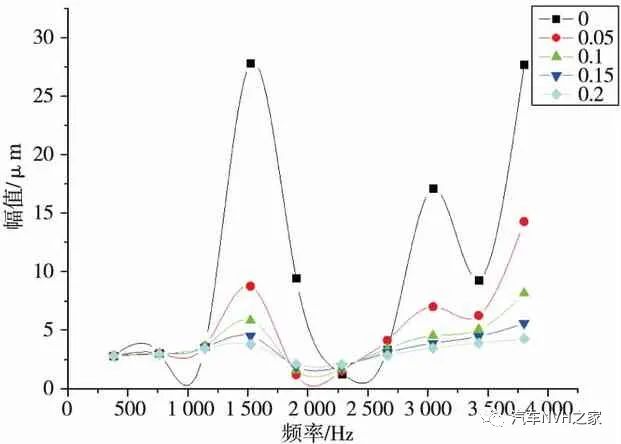
(b)刹车片振幅随频率波动曲线

图2 不同阻尼比的制动器振幅随频率波动曲线

由图2(a)可知，盘式制动器制动盘在零阻尼的情况下X方向振动幅值波动较大，其中频率在1 500 Hz时，幅值陡然上升，达1.4 μm，而其他频率下振动较为稳定。由图2(b)可知：制动块在不同阻尼比下振动幅值都相对较大，和制动盘一样，零阻尼状态的制动块幅值波动最大，分别在1 500 Hz和3 800 Hz时达到最大值28 μm；随着阻尼比的增大，制动块的振幅波动逐渐下降，阻尼比在0.2时幅值能基本稳定在5 μm以内。综合图2(a)和(b)可知，制动器在零阻尼比的情况下，频率在1 500 Hz时制动盘和刹车片振幅都出现最大值，此频率下两部件极易产生共振，引发制动噪音。

03盘式制动器振动噪声试验及结构改进

3.1 制动器制动噪声性能试验

盘式制动器噪声性能试验采用Dynamometer-GIANT 8600惯性制动试验台。该试验台具有密闭双层舱结构，可测量制动器在不同速度、温度及压力下的制动性能[12]。通过改变试验舱内温度、湿度及风速等参数，以模拟汽车在实际路面行驶过程中的工作环境，试验结果与真实结果较为接近。本试验以国际通用SAE J2521标准为试验规范。该标准主要分3个阶段，分别是常规制动阶段(0～1 430次)、冷态制动阶段(1 431～1 890次)和衰退后制动阶段(1 891～2 377次)[13]。本试验分前进和后退两个基本制动工况，按权重确定相应的试验次数，其中前进制动2 197次，后退制动198次。噪声采集装置简易图如图3所示，噪声采集器置于制动盘中心水平方向100 mm，垂直距离500 mm处，用噪音发生度(声压级SPL大于70 dB)来统计噪声出现的频率[14]。由于设备本身原因，该装置能采集的频率范围为2～17 kHz。未贴有消音片的制动器噪声声压级随频率的分布情况及不同制动阶段下噪声的分布情况如图4、5所示。

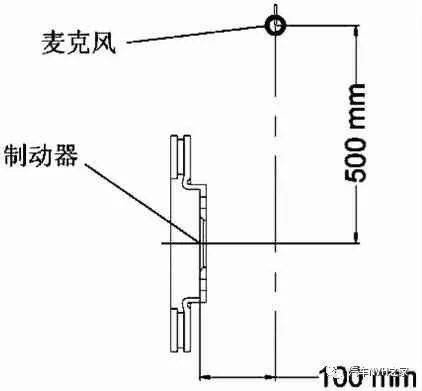
图3 噪声采集装置简易图

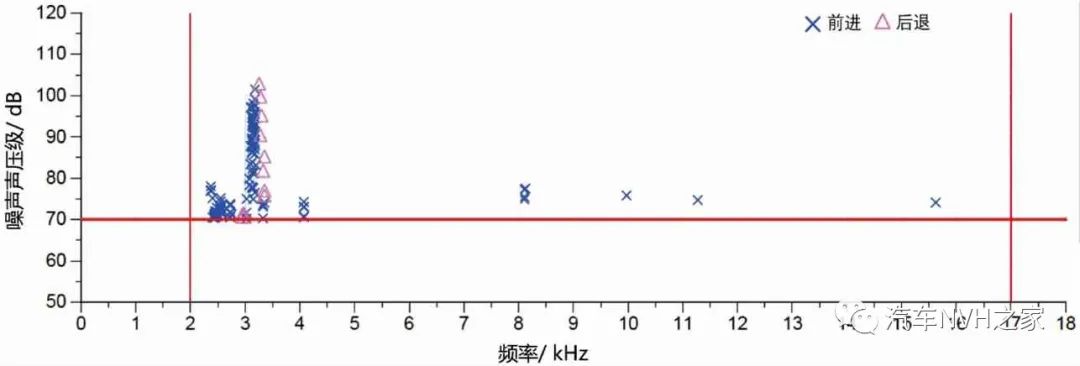
图4 未贴有消音片的制动噪声声压级随频率的分布情况

由图4可知：未贴有消音片的制动器制动噪声主要分布在振动频率为2～4 kHz，其中频率3 kHz左右时噪声最为密集，且声压级也较高，最大的达到105分贝；从前进和倒退的角度看，前进制动共出现119次，占总前进制动的5.5%，后退制动11次，占总后退制动的5.6%。图5显示了不同制动阶段下噪声的分布情况，折线代表了不同制动工况下制动盘表面的温度情况。可以看出，不管是前进还是后退制动工况，制动噪声大部分分布在冷态制动阶段，共出现122次，占总冷态制动的26.5%，远远超过了国内外汽车主机厂商对噪音发生度(SPL>70 dB)不大于5%的标准。

3.2 制动块消音片结构的改进

基于上述理论及仿真分析，改变制动器的阻尼比能降低部件的振幅，减少部件间的共振，从而达到降低制动噪声的目的。本文主要通过在钢背面粘贴消音片的方法来改变部件阻尼比，如图6所示，(a)为改进前未粘贴消音片的制动块，(b)为改进后粘有消音片的制动块。然而，目前市场上常见的消音片结构比较单一，单独的钢片或者钢片上附加一层橡胶的结构[15]。传统的消音片在常态工况下有一定的效果，但是在一些冷态工况或高温后常常表现不出多大的作用。本文主要以奥利奥为原型，提出一种夹心式消音片，其结构从钢背起，由胶水-钢片-橡胶-钢片复合组成，并进行热处理。经测量，该复合结构的消音片厚度约为2 mm，用LabVIEW通过自由衰减法测得该阻尼比约为0.2，由于橡胶在两钢片层中间，在增加阻尼比的同时又能保证消音片在不同环境温度下材料的稳定性。

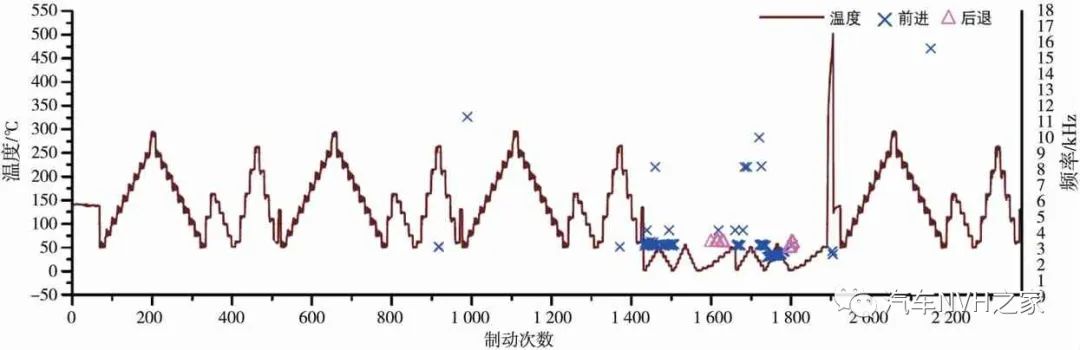
图5 未贴有消音片的制动器在不同制动阶段下噪声分布情况

图6 改进前后制动块实物图

3.3 消音片结构改进前后试验分析

在Dynamometer-GIANT 8600惯性试验台上分别对传统的消音片和夹心式消音片的制动块进行噪声测试试验，改进前后各工况下噪声发生度试验结果如表3所示，噪声与振动频率及其分布情况如图7—10所示。

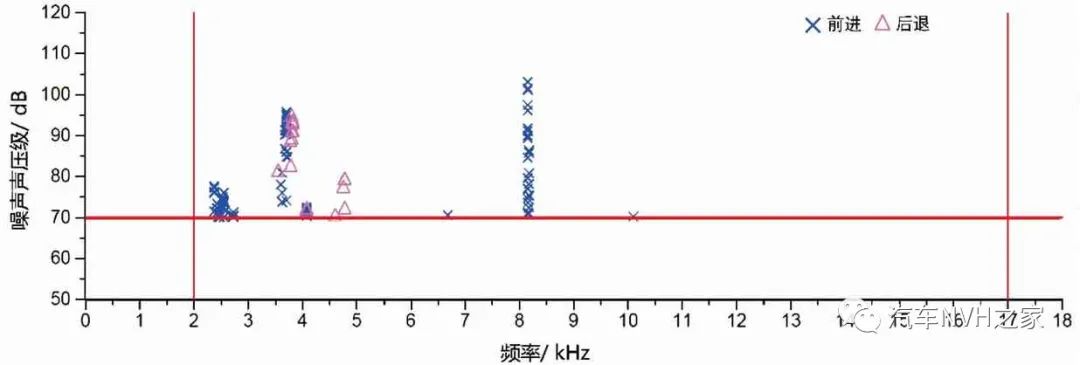
图7 传统消音片的制动噪声声压级随频率的分布情况

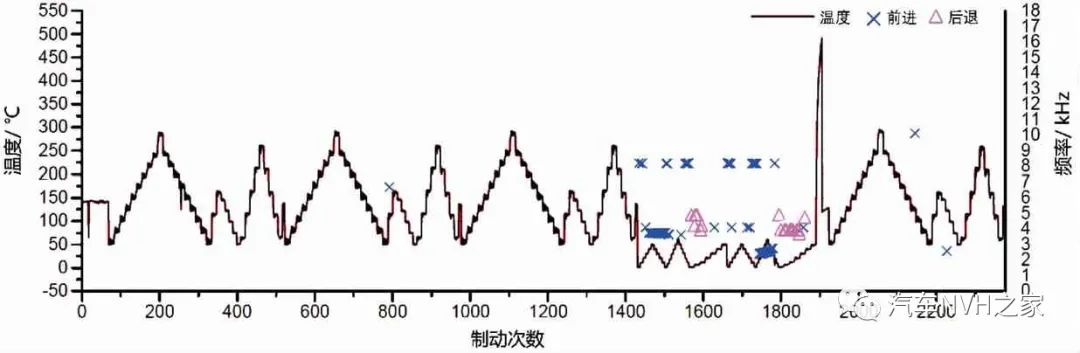
图8 传统消音片的制动器在不同制动阶段下噪声分布情况

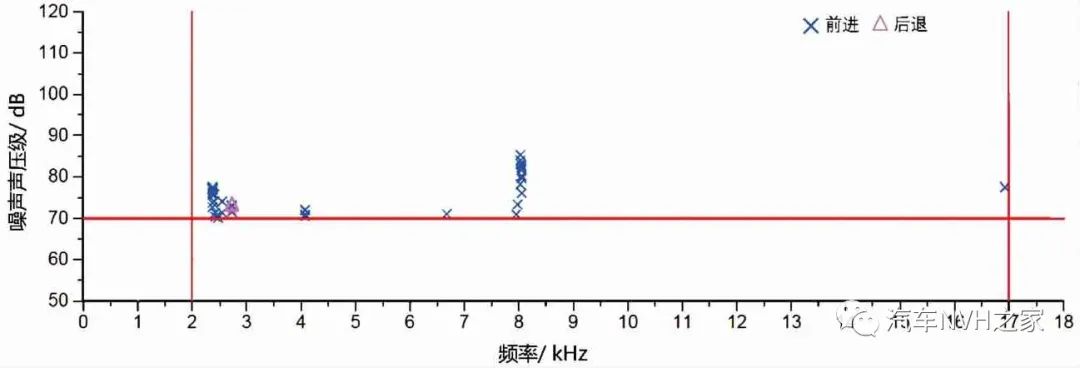
图9 夹心式消音片的制动噪声声压级随频率的分布情况

图10 夹心式消音片的制动器在不同制动阶段下噪声分布情况

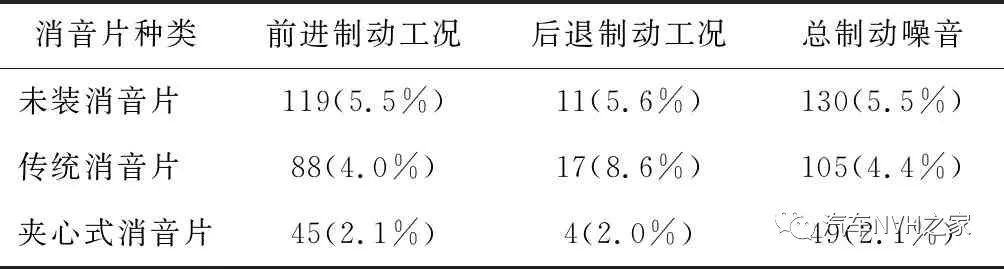
由表3可知：未安装消音片的制动器在测试过程中总的制动噪音共出现130次，占比5.5%；而安装了传统的消音片，即钢背和橡胶双层结构的消音片，测试中产生的振动噪音有所下降，前进制动工况噪音共出现88次，后退制动工况出现17次，总的制动噪音占比4.4%，比未安装消音片的制动块降低了1.1%。同样，从表3可看出夹心式消音片对制动噪声的影响更为明显，无论前进还是后退制动工况，制动噪声都降到了2.0%左右，相对传统的消音片噪声减少了一半。

表3 消音片对制动噪声影响情况

由图7可看出：传统消音片制动噪音主要分布在频率为2.5、3.6 和8.2 kHz左右，前进制动噪声频率分布得较为分散，而后退工况主要集中在3.5～5 kHz之间；制动的最大声压级相对无消音片的制动块没有降低，最大也超过了100 dB。图8显示了传统消音片在不同制动阶段的噪音分布情况。可以看出传统消音片的制动块制动噪音还是主要分布在冷态试验阶段。由图9可知，装有夹心式消音片的制动器制动噪声明显减少，且声压级也明显降低，最高只有86 dB。图10可看出夹心式消音片在冷态制动阶段的制动噪声相对传统的消音片降低了很多。虽然在衰退后制动阶段有些许的噪声，可能由于消音片的橡胶层在高温烧蚀后，两钢片间的轻微摩擦所致[16]，但总的来说，相对于传统的消音片，装有夹心式消音片的制动器制动噪声降低了50%左右。

04结论

1)盘式制动器制动噪声与制动器的阻尼比有关，阻尼比越大，制动盘与制动块的幅值波动越小，部件间共振的可能性降低，系统相对越稳定。

2)未安装消音片的制动器在冷态试验阶段振动噪声较为密集，约占总试验次数的26.5%，且主要集中在频率为3 kHz左右。

3)钢-橡胶-钢结构的夹心式消音片相对于市场上传统的消音片制动时产生的振动噪声在冷态试验阶段有明显改善，出现噪声的频率约占总制动次数的2%左右，整体性能相对传统的消音片提高50%左右。