在试验模态（二）中我们基于单自由度系统，说明了频响函数峰值频率与固有频率的关系，以及用半功率带宽法进行阻尼识别的精度和误差，内容主要涉及模态频率和模态阻尼这两个参数。今天，我们将介绍一个与模态振型相关的概念——“留数”。

—— 1#老枪
留数的英文单词是residue，首先请大家留意和模态分析中带宽外的上下残余项（residual term）区分开。residue和residual两个单词中文虽然都是“剩余”的意思（前者是名词，后者是形容词），但留数和上下残余项在模态分析中是两个完全不同的概念，二者没有任何关系。 在模态相关的书籍中，在动力学方程推导后，都会直接给出传函的极点（λ）和留数（A）的表达形式（公式1），从而给出结构响应是各阶模态线性叠加的结论，但很少说明极点和留数这两个概念的由来。                                                                          

 
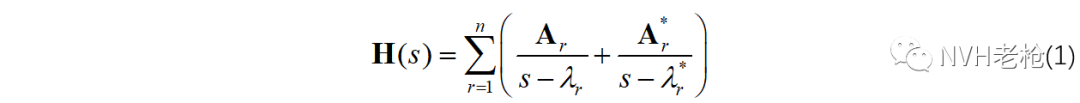
对于没学过《复变函数》的人而言，极点和留数是两个陌生的概念。此外，“留数”的本来应用是复变函数的积分运算，而模态分析理论中好像并没有明显涉及这个应用。因此，本篇文章将试图就极点和留数这两个概念的由来，以及在结构模态领域的应用进行简单阐述，可作为一般模态理论书籍这方面数学理论基础的一个补充。如果读者希望更详细了解复变函数相关的数学理论背景，可参阅参考文献[1]。
这篇文章偏理论，凡牵涉理论，尽管作者想尽量用通俗的语言表述，但鉴于数学概念的严格性，总是阅读起来会显得晦涩难懂，读者通常都容易半途放弃阅读。先打个预防针，建议感兴趣的朋友留出足够的时间（≥0.5小时），在电脑上阅读，甚至反复阅读。

1

模态理论的不同应用

首先，因为模态理论涉及的数学方程、公式比较多，因此我们有必要先从整体上理清一下模态理论在不同场合的应用。

 我们先说说CAE仿真计算所牵涉的模态理论。对于结构动力学仿真，常见的有两种分析： 1）模态分析：对于材料参数及几何参数已知的结构，通过有限元建模，可以构建出其质量矩阵、刚度矩阵，从而得到多自由度系统的自由运动方程。有限元模态的求解实际上就是通过矩阵运算对自由运动方程求解。求解完成后，即得到模态频率和模态向量。 2）动力学响应分析（直接求解）：基于运动方程，通过质量矩阵、刚度矩阵、阻尼矩阵以及力向量的矩阵运算，在每个分析频率步长下求解运动方程，依次计算得到结构的位移响应； 3）动力学响应分析（模态叠加法）：基于各阶模态参数及输入的模态阻尼信息，基于模态线性叠加理论，先得到各输入自由度到输出自由度的频响函数，而后再计算出输入力引起的结构振动响应。模态叠加法实际上并不依赖于有限元，不牵涉复杂的矩阵运算，所以计算速度非常快；此外，模态叠加法可以直接基于试验模态结果进行，只是试验模态中的自由度个数相对有限。 下面，我们再来说说通过试验获取模态参数的过程。首先对于试验模态而言，结构的质量、刚度、阻尼特性都是未知的，因此不可能构建出结构的运动学方程，也就不可能通过求解运动学方程来求取模态参数。 试验模态的数据基础只有通过试验获取到的输入到输出的频响函数。那么怎么通过频响函数去识别极点（模态频率/模态阻尼）、模态振型等参数呢？ 这就需要把频响函数表示为一个包含这些待求参数的数学模型。这个数学模型当然不是随意构建的，它必须能够真实反映频响函数的相关特性。实际上，在下文中我们将看到，频域试验模态参数识别方法，通常就是将传递函数的有理函数形式作为其数学模型；而时域模态参数识别方法，则是将极点留数形式的单位脉冲响应函数作为数学模型。 利用试验获得的频响函数（或转化为单位脉冲响应函数）的各频谱（采样点）数据，根据包含代求参量（模态极点、留数/振型向量）的数学模型，逐一列出方程，然后进行方程组求解，从而确定出各阶的模态参数。这个过程，很多书上称之为曲线拟合（Curve Fitting）。 极点留数概念是模态线性叠加理论的根源，更是试验模态分析中传递函数数学模型的基础，是模态理论中的关键概念，值得我们深入了解。

2

留数概念从何而来？

留数概念来源于数学理论，最早由法国数学家柯西在研究复变函数积分理论时所提出。所谓复变函数就是以复数为变量的函数。在模态分析理论中，通过对运动方程进行Laplace变换，得到以复频率为变量的传递函数，显然就属于复变函数。 对于一个复变函数，在其孤立奇点λ（对有理函数而言就是极点）的去心邻域内，可以用洛朗级数进行展开，如公式(2)所示。

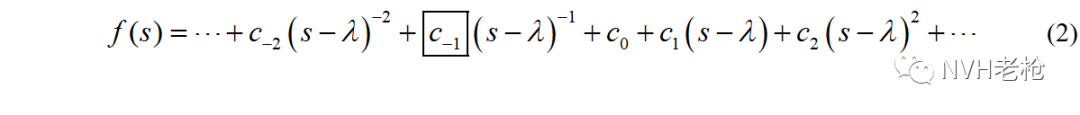
所谓的洛朗级数，类似于傅里叶级数、泰勒级数，也是一种函数的展开形式，只是在我们所熟悉的泰勒级数基础上，进一步拓展了负幂次项。从而使得函数不仅能在泰勒级数收敛半径内展开，还可以在整个复平面解析范围内展开。

 其中，公式(2)中洛朗级数的－1幂次项系数c－1被称之为该孤立奇点 λ 所对应的留数。之所以取名为“留”数，是因为根据等式(2)，如果对函数f(s)在λ去心邻域内进行积分，结果中将只有这个(s－λ)－1项残留下来，其他次幂项积分后都将为零，如公式(3)所示。（证明过程参见附录1）。

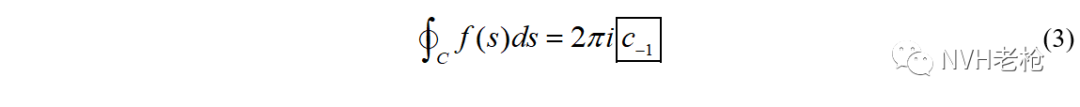
由此，定义 f(s)在极点λ处的留数为：

 如果f(s)在某区域内包含有多个（如n个）孤立奇点，可证明函数在区域内的积分与各极点处留数的关系为：

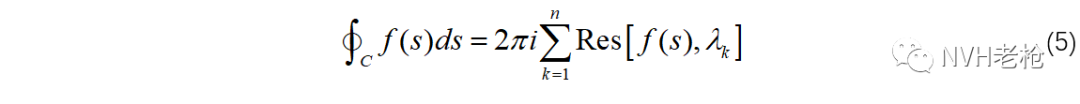
 这就是大名鼎鼎的留数定理。有了留数定理，就可以解决很多不定积分、定积分的问题。在信号处理中的典型应用之一就是用留数定理计算复变函数的Laplace逆变换（证明过程见附录2）：

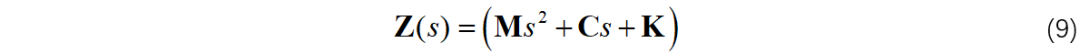
 上面这个公式(6)我们将在下一节中用到，请大家留意。

3

留数与传递函数怎么扯上的关系？

上一节我们说明了留数概念的起源，但要弄清楚留数与模态分析有什么关系，还需要从结构的运动方程说起。

多自由度系统的运动方程为：

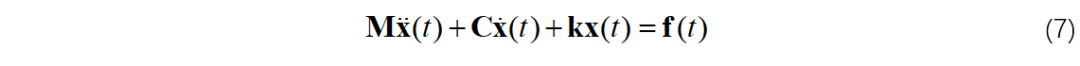
其中，M，C，K分别为质量矩阵、阻尼矩阵和刚度矩阵。

对等式(7)两边进行Laplace变换，可得：

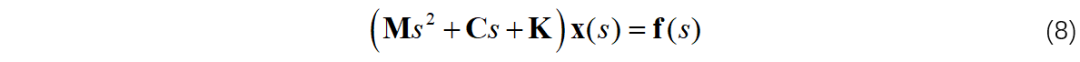
其中，位移向量x(s)前的系数矩阵即为动刚度矩阵：

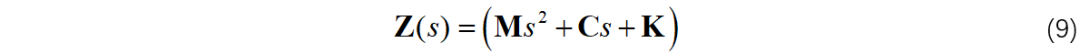
由载荷输入、位移响应、传递函数的关系，可知：

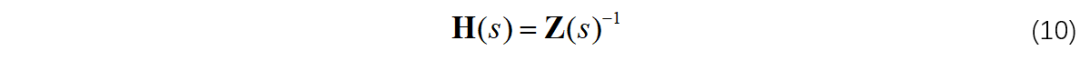
根据线性代数理论，矩阵求逆可通过其伴随矩阵及行列式进行求解：

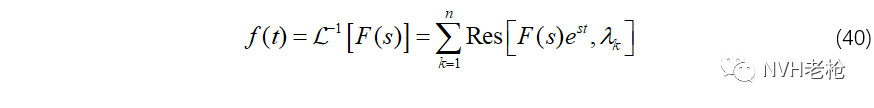
其中，|Z(s)|是动刚度矩阵的行列式，adj[Z(s)]是动刚度矩阵的伴随矩阵。

 对于n个自由度的系统而言，H(s)、Z(s)以及adj[Z(s)]均是n×n的矩阵。观察动刚度矩阵Z(s)中元素的构成，可知：

• Z(s)矩阵中每个元素最高次项为s2，因此行列式| Z(s)| 是最高次项为s2n的多项式。

• 伴随矩阵中的每个元素对应的是矩阵行列式中相应位置元素的代数余子式，因此adj[Z(s)]矩阵中每个元素是最高次项为s2(n-1)（或更低次项）的多项式。

 因此，传函矩阵H(s)中各自由度间的每个传函均为有理函数，其分母是最高次项为s2n的多项式（且均相同），分子是最高次项为s2n-2的多项式（但各不相同），如公式(12)为矩阵中某一个传函的具体表达形式。

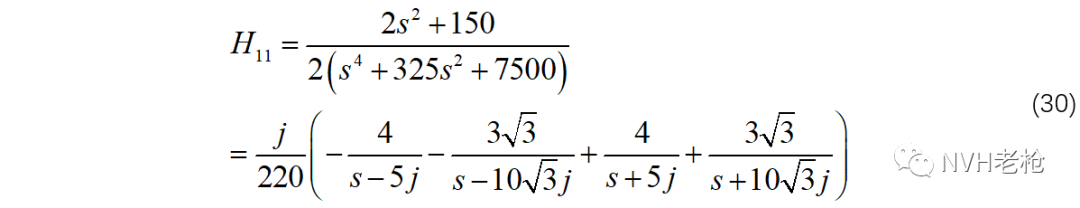
对应分母多项式的n对共轭零点，传函有n对共轭极点：λ1，⋯，λn；λ1*，⋯，λn*。因为每个传函的分母多项式都是一样的，因此有相同的极点，也就是说传函的极点反映的是系统的整体特性。
实际上在试验模态分析中，正交多项式法（OP）、最小二乘复频域法（LSCF及PolyMAX）等频域模态极点识别算法，所基于的传递函数数学模型正是公式(12)中的有理函数形式。根据分析带宽内各谱线上的数据逐个列方程，构建方程组，求解出分母多项式中的各项系数a0，a1，……，an，再进一步求得极点。 公式(12)中分子多项式对应的是adj[Z(s)]矩阵中的某个元素，因此不同自由度间传函的分子多项式显然各不相同。对应n对共轭极点，每个传函都有各自的n对共轭留数：A1，⋯，An；A1*，⋯，An*。根据公式(6)，用留数定理对公式(12)中的H(s)进行Laplace逆变换，即得到其时域脉冲响应函数h(t)：

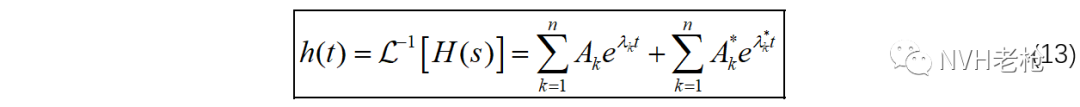
注意公式(13)，实际上就是试验模态分析中时域方法（最小二乘复指数法，LSCE）所使用的数学模型。根据单位脉冲响应函数上各采样点的数据逐个列方程，然后再借助Prony多项式构建自回归模型，即求得极点。
对公式(13)两边重新再进行Laplace变换，可得：

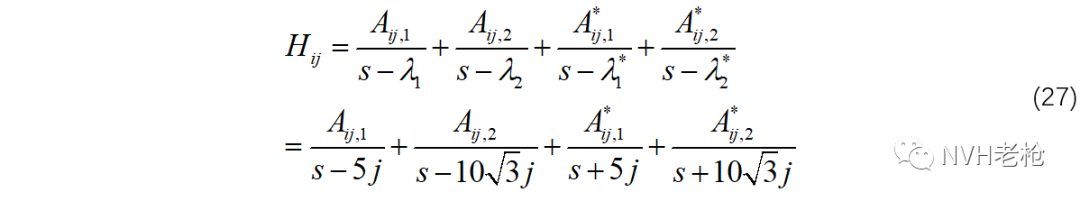
而我们知道  ，带回公式(14)，由此就得到我们所熟悉的传函的留数表达形式：

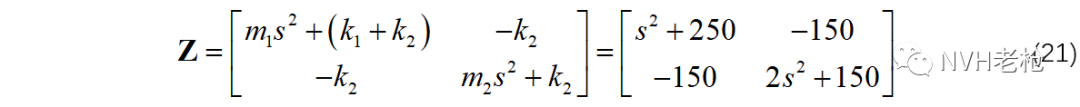
仔细观察公式(15)，我们会发现，留数（Ak）实际上就是将传函进行部分分式分解后，各一次分式函数（分母一次项系数为1）的系数。这看似是一种巧合，实际是一种必然。因为对于传递函数而言，其极点均是一阶简单极点。 因为在各极点处每个频响都对应有自己的一组留数，所以留数反映的是各个自由度的局部特性。此外，将传函表示为极点留数形式后，观察线性加和中的每一项（如  ），不正是极点为λk的某单自由度系统的传递函数么？因此，多自由度系统各自由度的动力学响应，均可以被分解到各阶模态极点下，是各阶模态下某单自由度系统响应的线性叠加。这就是模态线性叠加理论。
 

4

留数怎么计算得到？

 对于留数的求解，当极点为一阶极点时，可以直接用求极限方法（规则I）来求取：

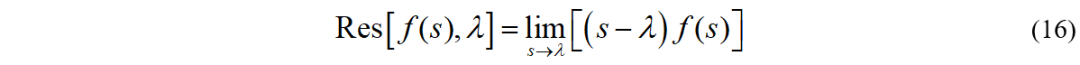
特别地，对于传递函数这样的有理函数：

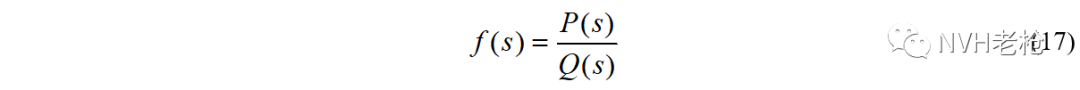
其中，Q(s) 为s的2n次分母多项式，P(s) 为s的2n－2次分子多项式。对应各一阶极点，可利用分母多项式求导法（规则III）来计算留数：

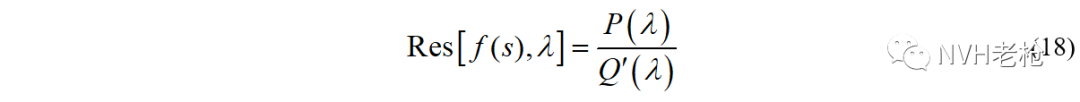
5

一个两自由度系统的实例

下面，为了对极点和留数有更具体的认识，我们以如图1所示的两自由度无阻尼系统为例，来说明极点和留数的计算过程。m1 = 1kg，m2 = 2kg，k1 = 100N/m，k2 = 150N/m。

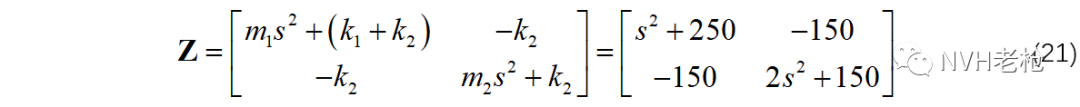
图1两自由度无阻尼系统示意图
系统的运动方程为：

对上式进行Laplace变换：

得动刚度矩阵为：

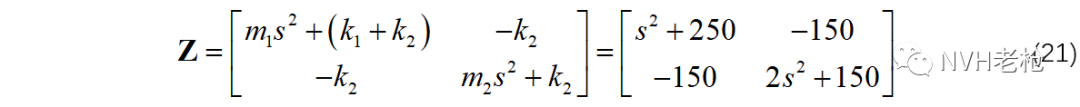
传递函数为：

其中：

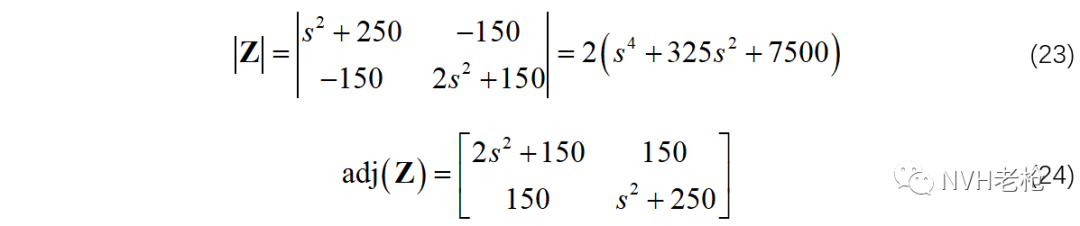
则：

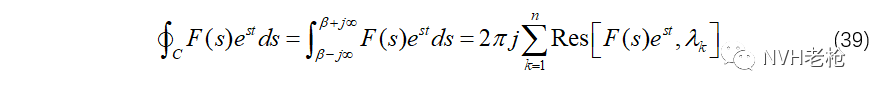
令  ，解方程，可计算得到传函的两对共轭极点为：

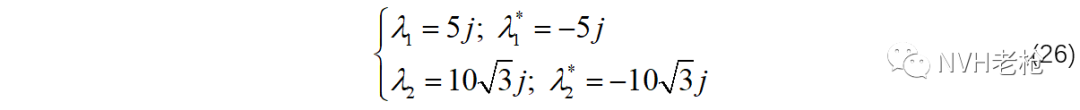
将传函表示为极点留数的形式（下标i，j分别对应输出和输入自由度）：

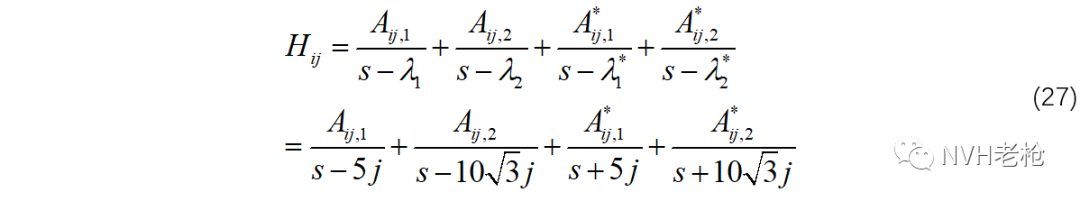
下面我们用求导法确定其中的留数。先以H11为例：

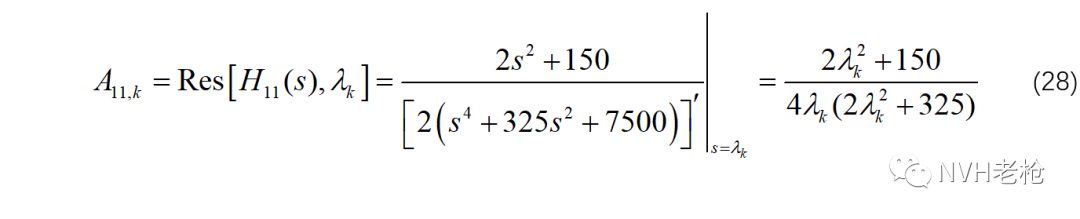
将(26)中各极点分别带入(28)，求得所对应的留数：

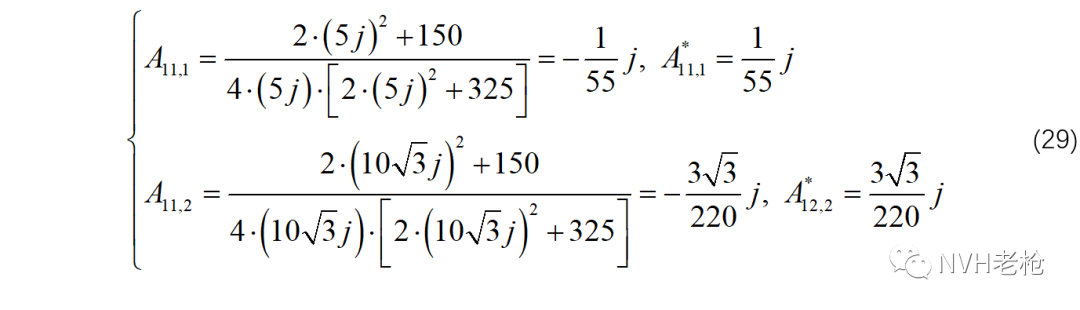
因此，H11的极点留数表达形式为：

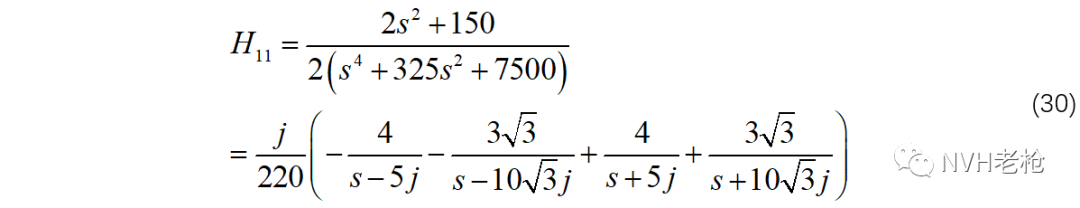
同理，可得H12，H21，H22的极点留数表达形式：

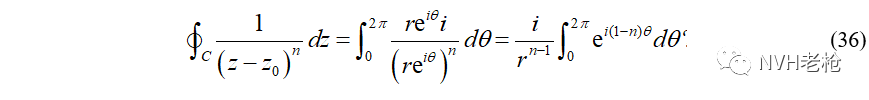
因此，传函矩阵H(s)可以表示为：

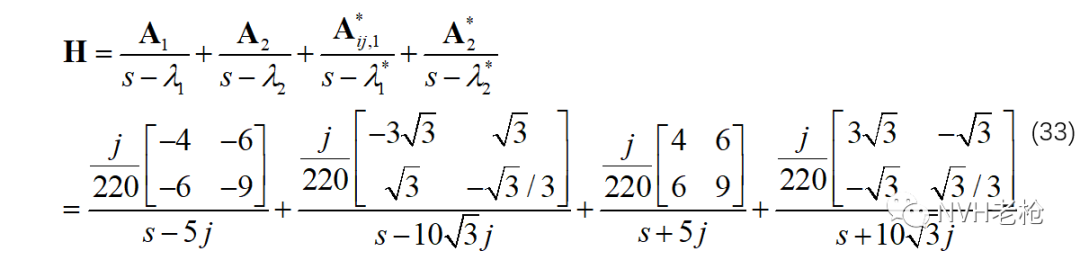
现在我们来观察最终结果中的留数矩阵，我们发现每行之间或每列之间都是等比例缩放的，相差的只是一个系数。比如  ，两行或两列之间的比例都是2 : 3。 这难道是巧合么？当然不是，其实这就是留数和振型向量之间的内在关系所在，这一点我们留待下一篇文章中再详细说明。 

6

小结

 本篇文章内容可用如下流程概括： 

 清明假期，国内疫情形式严峻，希望这只是新冠病毒的回光返照。上海、吉林等疫情比较严重地区的朋友们多多保重，希望大家的生活早日恢复常态！我们下期文章见！

附录1 留数定理的证明

证明：  （n为自然数），Γ为孤立奇点z0的任意去心邻域边界。
证：取C为  ，即绕奇点z0的一个闭合圆曲线，如图2所示：

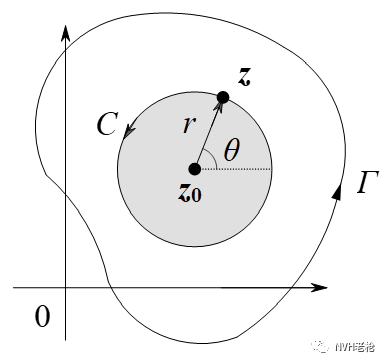
图2 绕奇点z0的构造一个闭合圆曲线C

C曲线的方程为：

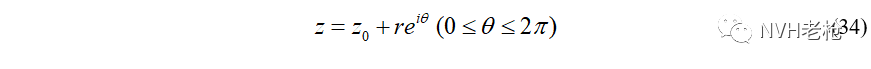
由柯西积分定理，知：

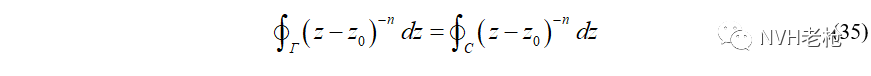
将(34)带入积分，得到：

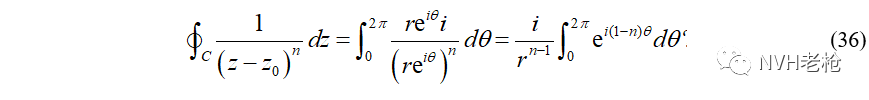
分别讨论 n = 1和 n ≠ 1的两种情况，即可得：

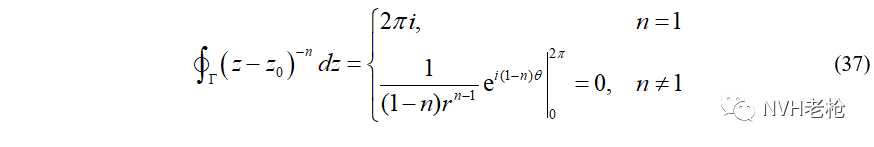
附录2 拉普拉斯变换留数表达的推导

拉普拉斯逆变换：

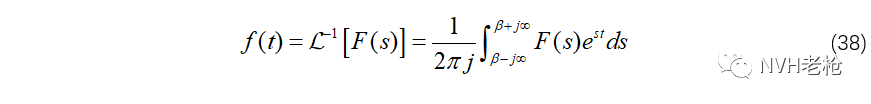
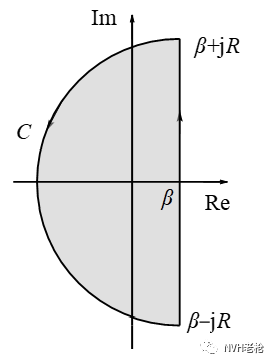
如图3，构造一个闭合区域（边界C由直线积分路径及半圆构成）：

图3 Laplace变换构造闭合积分区域
 由于当R→∞时，可证明半圆路径上的积分为零（若尔当引理），由公式(5)留数定理，可得：

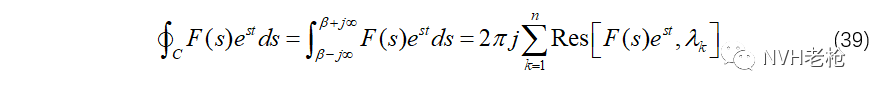
将公式(39)带回(38)，即可得：

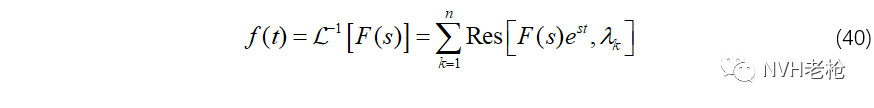
 参考文献1. 李红, 谢松法, 复变函数与积分变换.第5版. 2018: 高等教育出版社.