数据驱动的动态系统（Dynamical System）建模(一)：深度学习

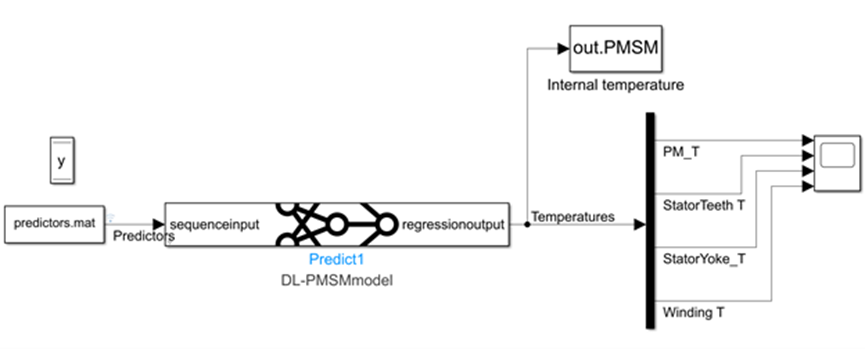
我们将训练好的模型保存为 .mat 文件，并将其导入 Simulink Deep Neural Network Predict 模块[链接9]，这样我们就有了一个只有 50Kbyte 大小可以预测温度的代理模型（Surrogate Model）用于仿真。

Neural Ordinary Differential Equations：神经网络 ODE

这是 NIPS 2018 年最佳论文[2]提出的一种新的网络层。当然这个要理论上介绍还是比较复杂，我们可以通过应用场景直观的解释一些 Neural ODE 如何实现动态系统建模。

试想我们有一个动态系统，因为系统动力学过于复杂，我们没有真正的物理模型，但我们可以不断地通过测量得到系统的初始状态 y(t0)，动态输 入 u(t0), u(t1),…, 与动态输出  y(t1),y(t2),…,y(tn)。接下来我们想是否可以实现这样一个微分方程：

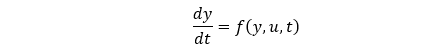
使得这个微分方程正好代表了我们的系统，也就是说在系统输入 y(t0) 的初始条件下通过求解(例如使用 ode45)这个微分方程得出的解 yp(t) 和我们实测结果是吻合的。但如何基于已有的数据 y(t0),序列 u(t) 和序列 y(t) 得到 f 呢？如果我们将 f 用一个神经网络 F(θ) 替代，即

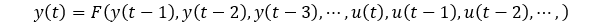
我们现在有数据 u(t), y(t)。我们不断地利用数据训练参数θ，使得上述方程的解 yp(t1), yp(t2),...,yp(tn) 与实测 y(t)是吻合的，那就可以得到这个动态系统的微分方程模型了，从而可以用于后续系统仿真与预测。如何理解  yp(t)  与实测 y(t) 的接近度,也就是损失函数? 我们简单介绍一下训练时 Loss 函数计算。对于方程，我们在知道系统初始状态 y(t0)，可以通过很多数值积分求解器（例如常用的 ode45）得到任何时刻的推断输出  yp(t) (当然前提是系统的输入 u(t)也是已知).

即

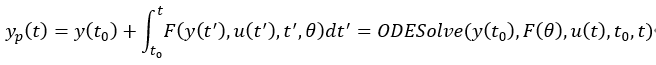
θ 是神经网络 F 的静态参数。对于所有时刻都是不变的。我们就可以方便得到损失函数的值

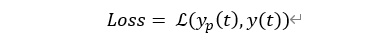
其中 L 可以是任何自定义的损失函数。于是我们可以进行参数 θ 的训练。当然关于梯度计算与反向传播会有相对复杂的数学推导，论文提出了伴随方法（Adjoint Method）来实现这一过程，此处不做详细论述。

对应于上述过程，MATLAB中提供了dlode45 [链接10]，用于建模方程右侧非线性函数F的同时，计算 ODE 的时序解。

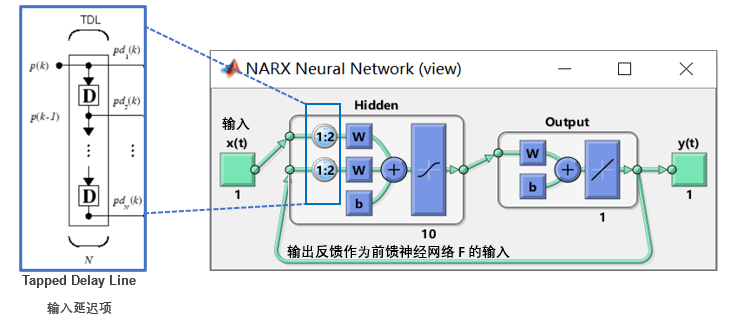
即 dlode45 接收一个含参神经网络 F(θ)、需要计算输出结果的时刻序列 [t0, t1,…,tN]、系统的 t0 时刻的初始状态 yt0、神经网络参数的一组值，就可以计算出时刻 [t1,…,tN] 所对应的输出状态。

使用 Neural ODE 为系统建模示例

我们通过一个示例介绍如何使用Neural ODE为动态系统建模。[链接6]

我们就借用文章刚开始的简单二自由度线性系统，x' (t)=Ax(t), 其中A是一个 2x2 的矩阵。我们用这个已知的系统产生一些数据，利用这些数据来训练一个 Neural ODE 的方程，使得这个基于数据训练好的系统（Neural ODE 方程）能够接近已知的这个动态系统。

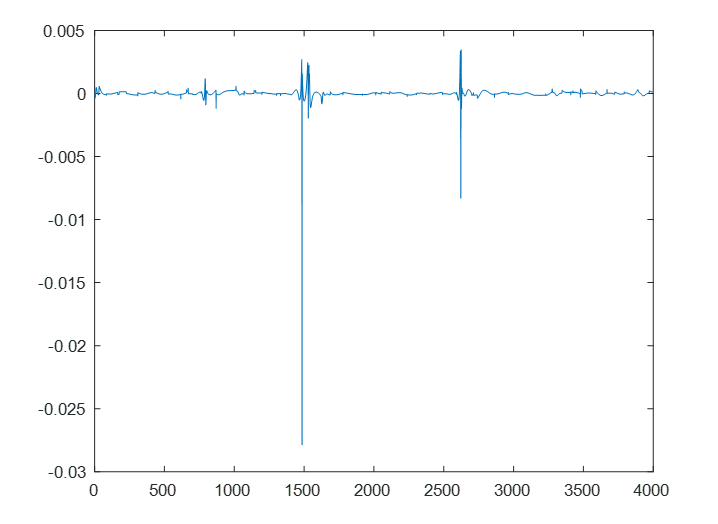
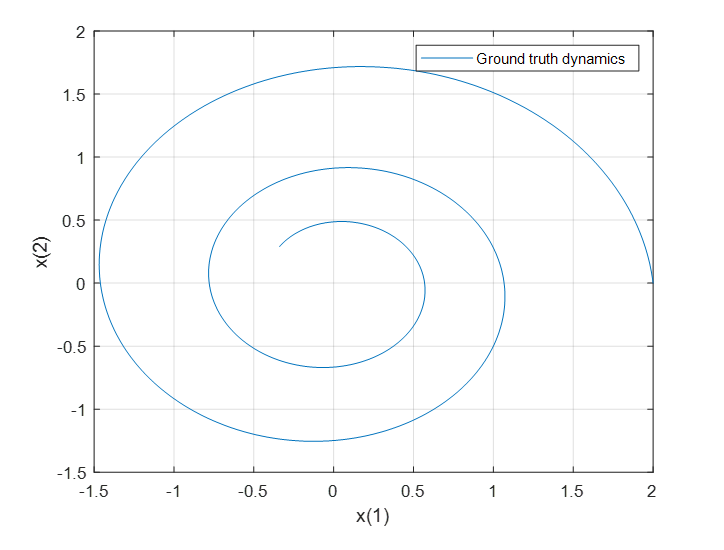
生成物理系统的数据 xTrain 作为真值

x0 = [2; 0];

A = [-0.1 -1; 1-0.1];

trueModel = @(t,y)A*y;

[~, xTrain] =ode45(trueModel, t, x0, odeOptions);

xTrain 两个自由度的可视化

定义和初始化神经网络 F(t,x(t),θ) 的参数 θ

neuralOdeParameters.fc1= struct;

sz = [hiddenSizestateSize];

neuralOdeParameters.fc1.Weights= initializeGlorot(sz, hiddenSize, stateSize);

neuralOdeParameters.fc1.Bias    = initializeZeros([hiddenSize 1]);

neuralOdeParameters.fc1

ans = 包含以下字段的 struct:

Weights: [20×2 dlarray]

       Bias: [20×1 dlarray]

同样

neuralOdeParameters.fc2

ans = 包含以下字段的 struct:

    Weights: [2×20 dlarray]

       Bias: [2×1 dlarray]

定义神经网络模型 F(t,x(t),θ) 函数

function y = odeModel(~,y,theta)

    y =tanh(theta.fc1.Weights*y + theta.fc1.Bias);

    y =theta.fc2.Weights*y + theta.fc2.Bias;

end

结合定义好的 F(t,x(t),θ) 作为 dlode45 的输入来构建代理模型函数

function X =model(tspan,X0,neuralOdeParameters)

    X = dlode45(@odeModel,tspan,X0,neuralOdeParameters,DataFormat="CB");

end

定义模型梯度函数

主要用于训练过程计算损失以及对应待训练参数的梯度

function [gradients,loss] =modelGradients(tspan,dlX0,neuralOdeParameters,targets)

    % Compute predictions.

    dlX = model(tspan,dlX0,neuralOdeParameters);

    % Compute L1 loss.

    loss =l1loss(dlX,targets,NormalizationFactor="all-elements",DataFormat="CBT");

    % Compute gradients.

    gradients =dlgradient(loss,neuralOdeParameters);

end

训练模型

不断地迭代训练，创建 miniBatch,并进行损失函数计算和自动微分，通过调用 adam 求解器进行参数学习

for iter=1:numIter

    % Create batch

   [dlx0, targets] = createMiniBatch(numTrainingTimesteps,neuralOdeTimesteps, miniBatchSize, xTrain);

    % evaluatenetwork and compute gradients

   [grads,loss] = dlfeval(@modelGradients,timesteps,dlx0,neuralOdeParameters,targets);

    % Update network

   [neuralOdeParameters,averageGrad,averageSqGrad] =adamupdate(neuralOdeParameters,grads,averageGrad,averageSqGrad,iter,...

       learnRate,gradDecay,sqGradDecay);

    % Plot loss

currentLoss =double(extractdata(loss));

…

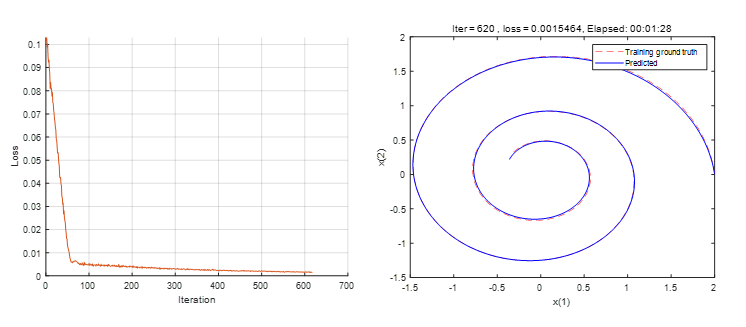
测试模型

选取新的初始条件作为训练好的模型的输入，来进行和物理系统输出的对比

x0Pred1 =sqrt([2;2]);

x0Pred2 =[-1;-1.5];

x0Pred3 = [0;2];

x0Pred4 = [-2;0];

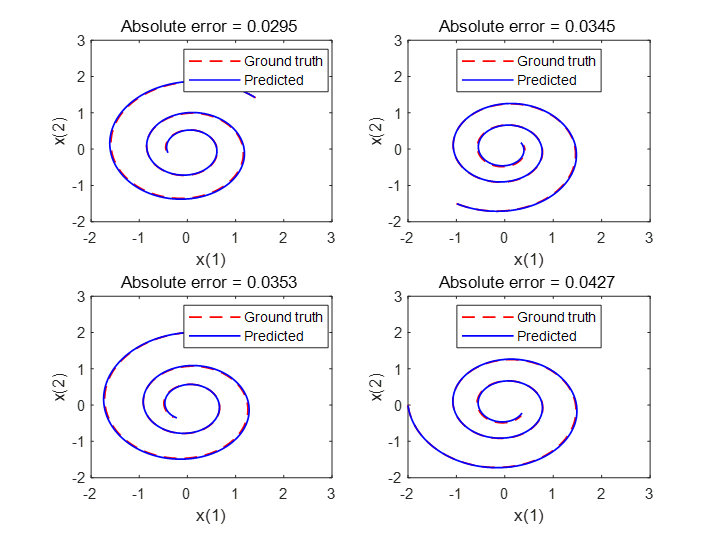
可以看到模型对于新的初始条件依然表现优异。因此神经网络 ODE 在构建动态系统上很有潜力，目前在发动机建模上也有一些示例应用。