广告
数据驱动的动态系统（Dynamical System）建模(一)：深度学习
在深度学习网络爆发之前，在浅层神经网络的场景中，NARX 反馈神经网络是经常用于动态系统建模的，它具有反馈连接，即输出 y(t) 依赖于系统之前时刻的输出 y(t-1)，y(t-2) 等等和输入。
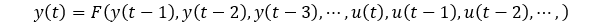
其中网络 F 主要是通过一个前馈神经网络实现。
如下图，其中F即为第一层隐含层前馈网络，其中输入和输出可以是多维的。
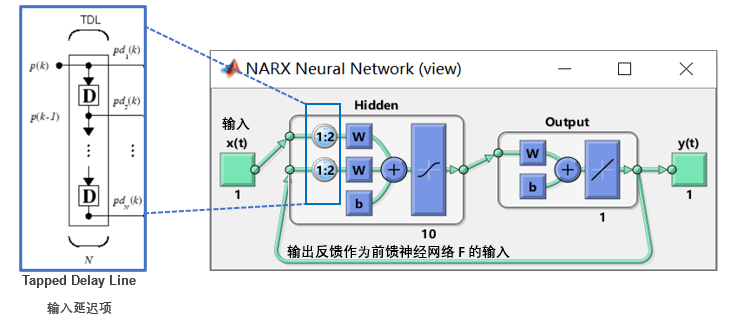
跟其他反馈神经网络类似（前面介绍的 LSTM）,它的训练过程与推断过程有些区别。网络本身的输出需要被反馈到前馈神经网络的输入。在训练时，因为我们能够拿到整段输出真实的数据，因此，我们会用当前时刻真实的输出值作为训练时模型输入而不是反馈预测的输出，换句话说，在训练时我们会把网络作为开环去训练。
这有两个好处。一是前馈网络的输入更准确。第二，生成的网络具有纯前馈架构，静态反向传播变得可用。当我们进行未来多步推断时，因为这种情况我们只能用推断的数据进行下一时刻预测，所以这次我们才把网络闭环，用于推断。
磁悬浮系统的 NARX 建模示例
接下来我们使用 narx 神经网络来对动态系统进行建模的示例[链接7]。示例系统是一个磁悬浮系统。目标是控制悬浮在电磁铁上方的磁铁的位置，在电磁铁的位置上，磁铁受到限制，只能在垂直方向上移动，如下图所示，
系统的运动方程为：
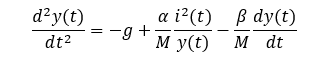
其中 y(t) 是磁铁在电磁铁上方的距离，i(t) 是经过电磁铁的电流，M 是磁铁的质量，g 是重力常数。其中 β 为粘性摩擦系数，由磁体运动材料决定；α 为场强常数，由电磁铁上导线匝数和磁体强度决定。我们搜集了系统输入 u(t)-施加在电磁铁上的电压和系统输出 y(t)-永磁体的位置，对应两个时间序列。
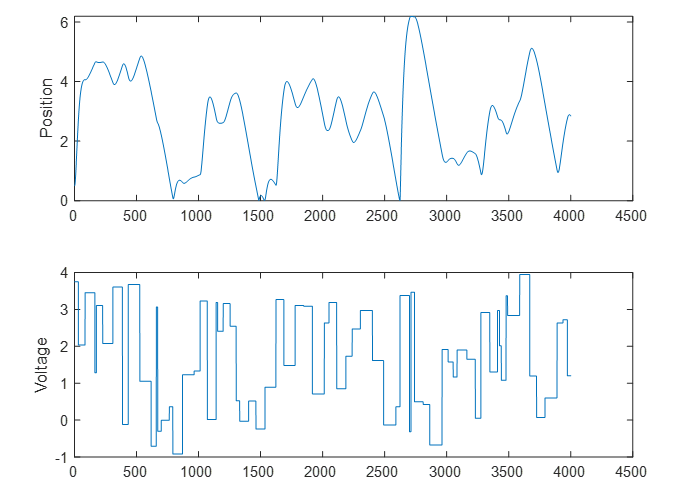
搭建网络和准备数据
d1 = [1:2];
d2 = [1:2];
narx_net =narxnet(d1,d2,10); % 使用narxnet功能创建NARX开环串联网络，10个隐藏层神经元
[p,Pi,Ai,t] =preparets(narx_net,u,{},y); % 用preparets准备数据
其中 y(t) 是一个反馈信号，既是输入，也是输出，训练时我们既可以拿到当前时刻数据，也可以拿到后面时刻的数据，所以可以用于开环训练，当推断时我们会将输出接到输入作为闭环进行推断。
训练网络
narx_net =train(narx_net,p,t,Pi); % 训练网络得到训练好的网络
验证开环网络推断效果
yp =sim(narx_net,p,Pi);
e =cell2mat(yp)-cell2mat(t);
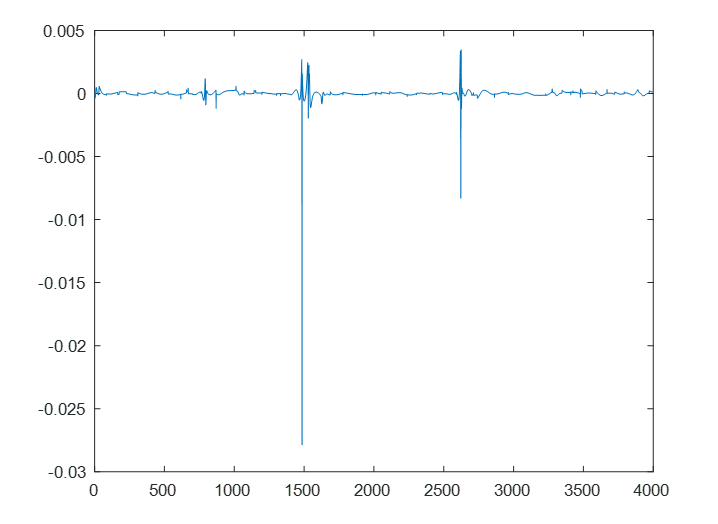
可以看到误差很小。因为我们用的开环训练，所以推断结果是用前面时刻的真实输出数据（而非推断输出反馈），所以这里的误差是 one-step-ahead 推断误差。
测试闭环推断效果
如果要看网络真实准确度的表现，需要将开环的输出作为反馈接到输入，然后进行多步预测。
narx_net_closed =closeloop(narx_net);
现在可以使用闭环执行 900 个时间步的迭代预测。在这个闭环网络中只需要两个初始输入和两个初始输出作为初始条件。
y1 = y(1700:2600);
u1 = u(1700:2600);
[p1,Pi1,Ai1,t1] = preparets(narx_net_closed,u1,{},y1);
yp1 =narx_net_closed(p1,Pi1,Ai1);
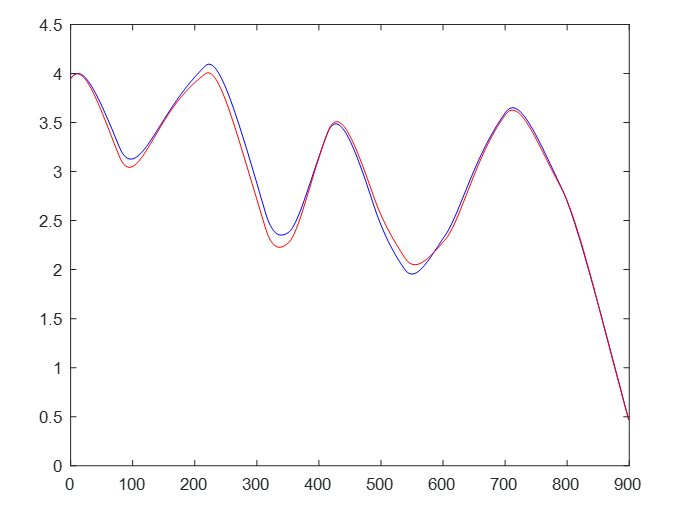
从闭环预测的结果看，蓝线是磁铁的实际位置，红线是 NARX 神经网络预测的位置。即使网络预测的时间步预测了 900 步，预测依然是非常准确的。闭环多步预测准确的前提就是开环下单步推断误差要小。
总结
本文主要介绍了动态系统的特性和用于动态系统建模的神经网络模型从而可以实现模型降阶（Reduced Order Modeling），包括前馈神经网络，TCN，循环神经网络，神经网络 ODE, NARX 网络和相应的一些手段，并结合示例与场景进行了说明这些手段的有效性。
在后续文章我会来介绍系统辨识（System Identification）的一些示例,欢迎继续关注。
- 下一篇：电流测量方法大揭秘
- 上一篇：强域控、超感知的均胜电子智能驾驶域控平台
广告
广告
编辑推荐
最新资讯
-
NVIDIA 发布 2025 财年第三季度财务报告
2024-11-21 13:30
-
Mack卡车为买家推出创新的虚拟现场探索体验
2024-11-21 13:29
-
氢燃料电池卡车从1到100要多长时间？戴姆勒
2024-11-21 13:28
-
聚焦消费者用车极限环境，2024中国汽研汽车
2024-11-21 13:21
-
新能源汽车高寒环境可靠性行驶试验研究
2024-11-21 13:19
广告
广告
