基于声品质贡献因子的发动机悬置优化

摘要:本文中建立了ＧＡ-ＢＰ 声品质预测模型，引入声品质贡献因子，以期通过传递路径分析更加直观地反映结构噪声传递路径对烦躁度的贡献情况和掩蔽效应对声品质的影响。采用两级优化方案，通过遗传算法确定与目标烦躁度值对应的目标传递函数，并进一步匹配悬置参数。结果表明，基于声品质贡献因子的发动机悬置优化方案可有效地改善车内声品质，降低结构路径对烦躁度的贡献量。

关键词：发动机悬置；声品质预测；传递路径分析；声品质贡献因子；遗传算法

随着时代的发展，汽车乘坐舒适性已成为人们购车的重要考量指标，这对车辆ＮＶＨ 性能提出了更高的要求。由于传统的以声压级为指标的噪声评价标准无法准确反映乘坐者对车内声音的主观感受，声品质的概念应运而生。

声品质的研究主要包括客观声学参量计算、主观评价试验以及在此基础上进行的声品质客观预测。目前，声品质的评价尚未有统一的评价标准，奥地利ＡＶＬ 公司提出了声压级、综合级参数、周期性测量、响度、尖锐度、粗糙度、脉冲度和声压分布等８类客观声学参量［１］；日本学者Ｎｏｕｍｕｒａ 等提出了响亮（ｌｏｕｄ）、轰鸣（ｂｏｏｍｉｎｇ）、强劲有力（ｐｏｗｅｒｆｕｌ）、豪华（ｌｕｘｕｒｙ）、动感（ｓｐｏｒｔｙ）等１２ 个描述声品质的词汇［２］；吉林大学苏丽俐在此基础上建立了基于多元线性回归、ＢＰ 神经网络、广义回归神经网络和支持向量机的声品质评价和预测模型并分析其优劣性［３］。

车内噪声是多个振动噪声源传递的噪声在车内共同作用的结果，为研究这类振动噪声路径问题，常采用传递路径分析（ＴＰＡ）方法。吉林大学赵彤航通过分析整车系统与子结构的传递函数关系建立了以车内噪声声压级为控制目标、基于传递路径分析的噪声评价模型［４］。

目前，ＴＰＡ 更多应用于以车内噪声声压级为评价指标的研究中，而以车内声品质为改善目标的ＴＰＡ 研究尚处于初步探索阶段。

针对上述问题，本文中开展了相关研究，基本分析流程如下：

（１）通过动静态试验获取相关路径传递函数和不同工况下的车内与各激励源振动噪声信号；

（２）选择较易实现非线性分析的ＢＰ 神经网络模型并引入遗传算法（ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ，ＧＡ）进行优化，建立了基于ＧＡ-ＢＰ 神经网络的声品质预测模型；

（３）由于发动机振动为车辆结构辐射噪声最大的激励源，故本文中选其作为研究对象，引入声品质贡献因子（ＳＱＣＦ），建立了以烦躁度为目标的发动机振动传递路径分析模型，并确定各路径贡献情况；

（４）以发动机悬置为优化重点，利用ＧＡ 算法搜索符合目标烦躁度值的发动机悬置传递函数，在此基础上进行悬置特征参数的优化匹配和验证，结果表明，悬置参量优化后的振动传递路径，可有效降低烦躁度，提高车内声音品质。

1、车内噪声ＴＰＡ分析

车内噪声主要来源有空气和结构两种传递路径，路径传递函数是ＴＰＡ 分析的重点，由于研究空气路径时所用白噪声抗干扰能力较差，在室外背景噪声干扰下所测传递函数会产生较大误差［５］，为更精确地确定结构路径对应的车内噪声情况，本文中相关试验均在整车半消声室内进行。

１.１ 空气路径传递函数

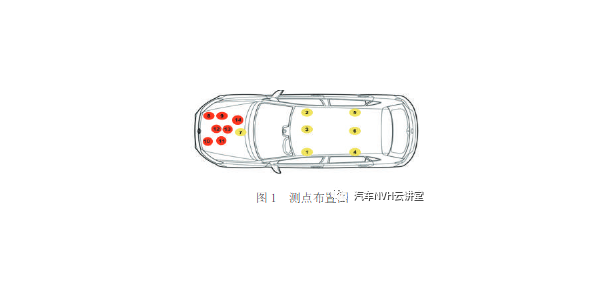
空气路径主要有发动机表面辐射噪声、进排气噪声、轮胎噪声和风噪，在半消声室内进行空气路径研究，可最大程度降低风噪的影响。考虑到噪声源较多，本文中根据互易原理，在样车上按图１ 所示的形式进行信号发生器和传声器的布置。

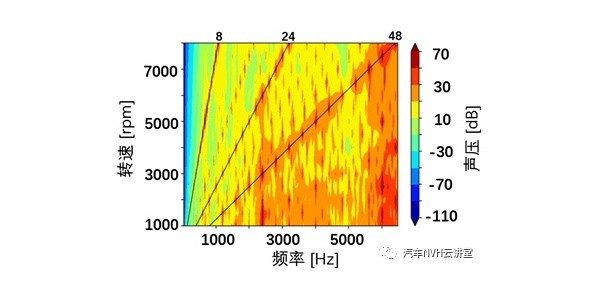
利用ＬＭＳ Ｔｅｓｔ．ｌａｂ 软件对信号进行采集和处理，得到各空气路径的传递函数，图２ 为所测发动机上表面辐射噪声传递函数。

１.２ 结构路径传递函数

车辆结构件的振动作为车内噪声的重要来源，主要包括发动机振动和路面激励。为使车内噪声合成结果更加精确，对这两种路径的传递函数均进行了测试。

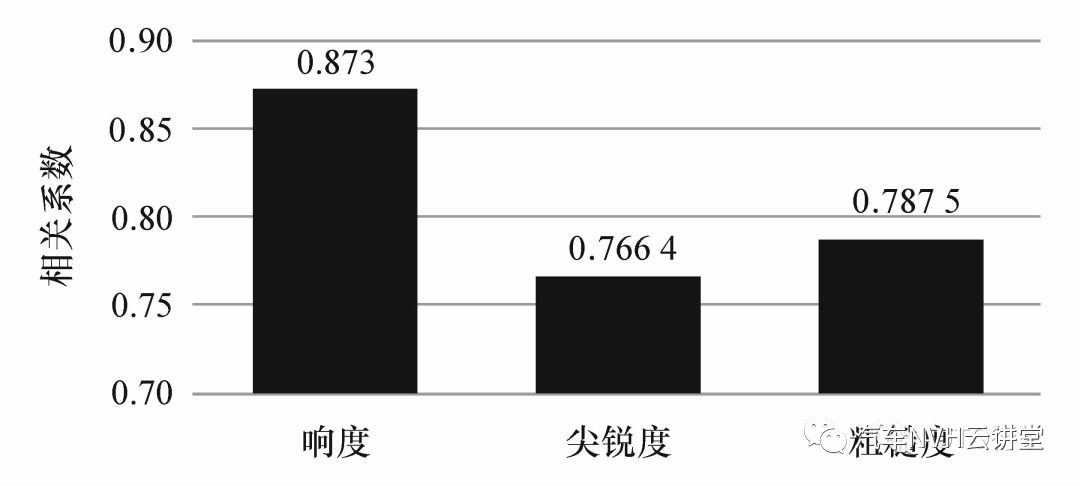
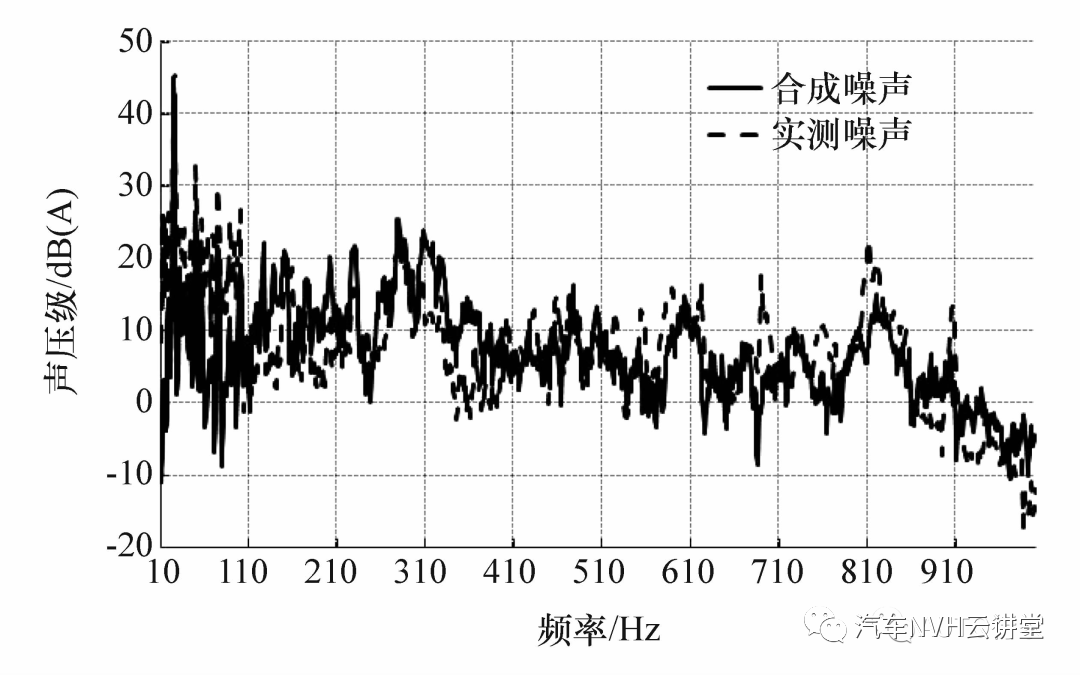
图２ 发动机上表面辐射噪声传递函数

主要包括发动机振动和路面激励。为使车内噪声合成结果更加精确，对这两种路径的传递函数均进行了测试。

发动机振动传递路径主要包括振动激励通过发动机悬置系统传递至车身和车身板件振动向车内辐射噪声两段，根据样车所用三点式悬置，将每一个悬置件的传递路径分为Ｘ、Ｙ、Ｚ ３ 个方向，确定发动机振动传递路径为９ 条，传递函数为

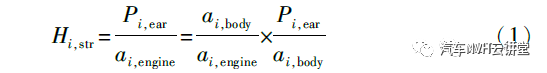
式中：ａi,engine为悬置结构与发动机连接端的振动加速度信号；ａi,body为悬置结构与车身连接端的振动加速度信号；Ｐi,ear为车内参考点的噪声信号。

根据式（１），在每个悬置的两端（连接发动机的主动端和连接车身的被动端）和车内参考点分别布置三向加速度传感器和传声器，通过力锤敲击相应位置，获得两段频率响应函数，结合为发动机振动路径传递函数。图３ 和图４ 分别为右悬置传递函数和右悬置与车身连接处到车内参考点的传递函数。

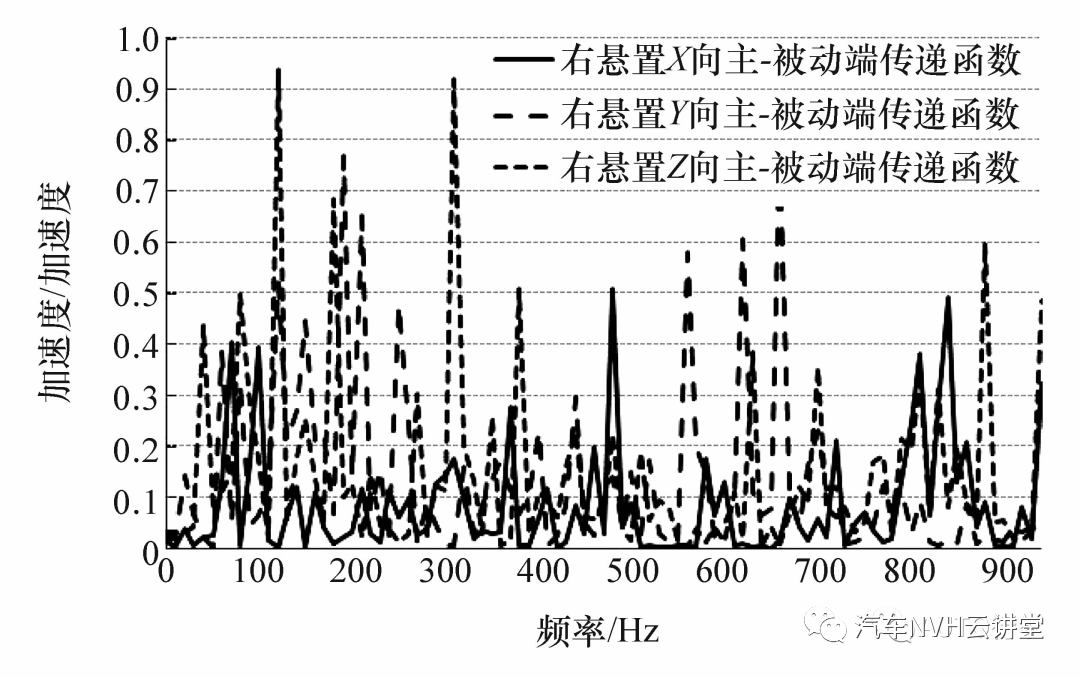
图３ 右悬置Ｘ、Ｙ、Ｚ 方向传递函数

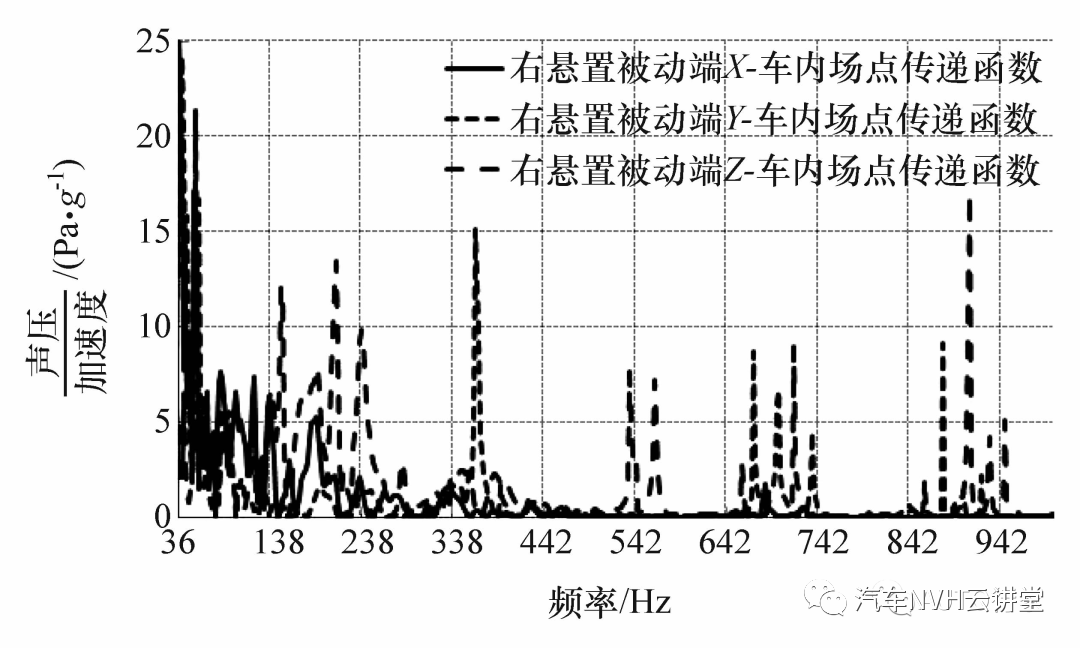
图４ 右悬置与车身连接点至车内参考点传递函数

按此测试方法，同时获取了路面激励的各路径传递函数。

１.３ 路径传递函数检验

为检验传递函数的准确性和满足后续研究的需求，在整车半消声室转鼓试验台上模拟车辆平直路面行驶状态。考虑到发动机噪声在车速100ｋｍ／ｈ以下时才是车内噪声的最主要来源［６］，根据ＧＢ／Ｔ１８６９７—２００２《声学汽车车内噪声测量方法》［７］，本文中模拟了怠速、20、40、60和80ｋｍ／ｈ 行驶工况，通过各工况2次15s的采集，记录相应的各激励源信号和驾驶员右耳旁噪声信号。

在ＴＰＡ 模块中将各激励源信号与所测对应路径传递函数相结合，合成出车内噪声信号，并与实测信号进行对比。图５ 和图６ 分别为整车转鼓试验和怠速工况下车内噪声合成与实测信号对比。由图６ 可见，合成信号的频谱分布和变化趋势与实测信号基本吻合，最大误差４ ｄＢ（Ａ），出现在２５ Ｈｚ处，这主要是由于频响函数测试时力锤低频特性较弱和未考虑部分次要路径的影响所致。综合分析，合成信号具有较好的拟合精度，所测传递函数可应用于后续研究中。

图５ 整车转鼓试验

图６ 怠速工况车内合成噪声与实测信号对比

2、车内声品质预测

车内声品质的研究须对试验采集的噪声信号进行客观声学参量计算和主观评价。为获得更多的数据样本，又挑选了２ 辆与前面样车同级别车辆，进行上述动态工况试验，共获取３０ 个车内噪声样本。

２.１ 客观声学参数与主观评价

为使声品质与ＴＰＡ 的结合更具参考性，对噪声样本进行通常的声学参量响度、粗糙度和尖锐度的计算，将其作为预测模型的输入，并以烦躁度作为评分指标，采用等级评分法进行主观评价试验。

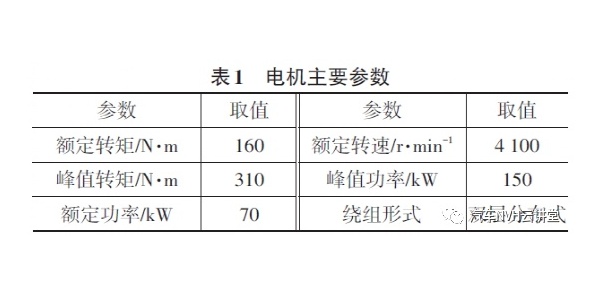
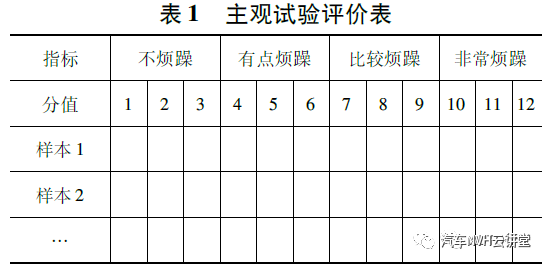
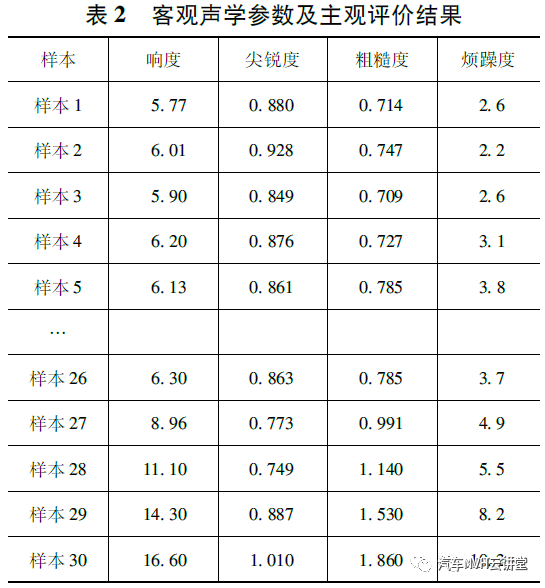
共有３０ 位高校相关专业硕士和博士研究生对３０ 个声音样本进行听音打分，其中男性１８ 人，女性１２ 人，年龄在２３ ～３０ 岁之间。考虑到部分人员听音经验较少，对评价等级进行简化，评价表如表１ 所示，表２ 为样本声学参数计算和主观评价结果统计。

2.２ 一致性与相关性检验

由于评价样本较多，且部分人员听音经验较少，须对评价数据进行一致性检验以剔除部分不稳定结果。采用一致性和相关性检验常用的ｓｐｅａｒｍａｍ 秩相关系数法：

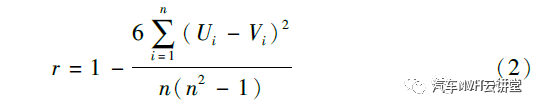
式中：Ｕｉ 和Ｖｉ 为两个不同变量的秩；ｒ 为秩相关系数。

图７ 一致性检验通过计算得到一致性结果，如图７ 所示。剔除其中与他人相关系数小于０.７ 的３ 个评价结果，将剩余２７ 人的烦躁值评价结果用于和声品质客观参数的相关性分析，结果如图８ 所示，可见响度、尖锐度、粗糙度与烦躁度之间均有超过０.７５ 的正相关系数。

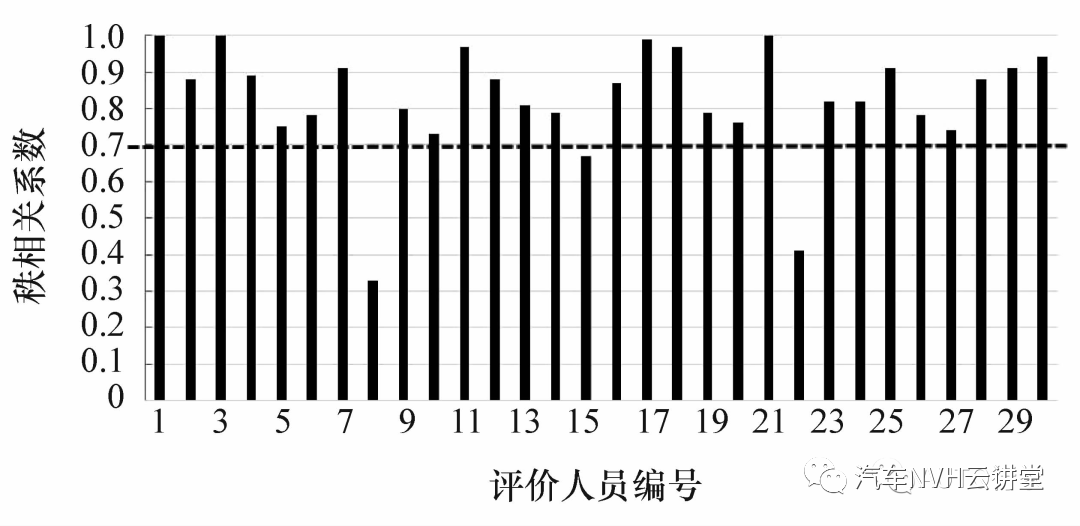
图７ 一致性检验

图８ 相关性检验

２.３ 声品质预测模型的建立

相关性分析结果表明，客观参量与烦躁度之间有着较强的关联性，为准确建立它们之间的关系并实现声品质的客观预测，本文中引入了一个３ 层ＢＰ神经网络，根据输入层节点数（３，响度，尖锐度，粗糙度）和输出层节点数（１，烦躁度），参考经验公式［８］，确定隐含层节点数为６，建立拓扑结构为３－６－１ 的神经网络模型：

式中：ｎ 和ｌ 分别为输入、输出层节点个数；ａ 为１ ～１０ 的常数。

为解决神经网络收敛慢和易出现局部极小的问题，引入轮盘赌选择法，采用种群规模２０、交叉概率０.３、变异概率０.１ 和最大遗传代数１００ 的ＧＡ 算法优化其初始权值和阈值。

为保证训练精度和验证结果的可靠性，随机选择２５ 个样本作为神经网络训练样本，剩余５ 个样本作为验证数据。通过学习效率０.１、训练目标１０－５ 的１００ 次迭代，获得结果如图９ 所示。５ 个验证样本的预测值与实测值误差分别为１.４７％、０.４８％、５.６４％、０.６６％和９.６９％，平均误差为３.５９％，证明声品质预测模型具有较高的准确性，可作为噪声声品质的客观评价依据。

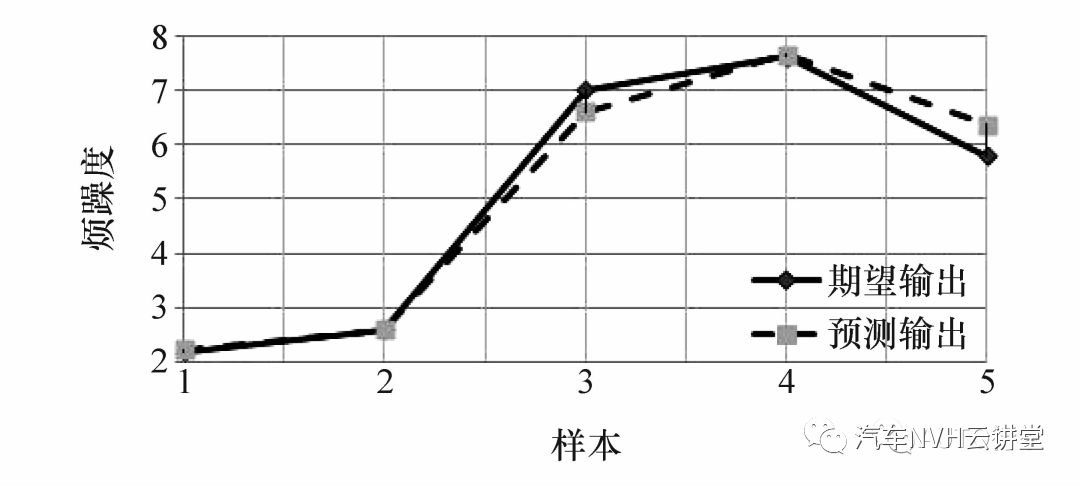
图９ 声品质预测模型检验

3、车内声品质贡献分析

频变Ｚｗｉｃｋｅｒ 法计算响度的公式为

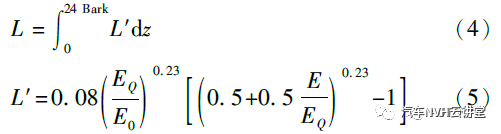
式中：ＥＱ 为安静听阈激励；Ｅ０ 为参考声强在10-12Ｗ／ｍ２下的激励。

由式（４）和式（５）可知，总响度为噪声频域信号在24Bark尺度下的特征响度积分所得，说明噪声信号是计算客观声学参量的基础，而前面的TPA分析已证明传递函数影响着车内噪声，故各路径传递函数与声品质具有一定的相关性。在此基础上结合ＧＡ-ＢＰ 声品质预测模型，完成了车内噪声结构传递路径对烦躁度的贡献分析。

３.１ 发动机振动路径声品质客观参量计算

由于前面已验证通过传递函数合成的车内噪声与实测噪声基本一致，故将由发动机各振动路径及其相应传递函数合成的噪声信号应用于贡献量分析。由于Ｓｏｕｎｄ Ｄｉａｇｎｏｓｉｓ 模块计算声品质客观参量采用时变Ｚｗｉｃｋｅｒ 法，本文中通过傅里叶逆变换（ｉｎｖｅｒｓｅＦｏｕｒｉｅｒｔｒａｎｓｆｏｒｍ，ＩＦＴ）将合成的噪声频域信号转换为时域信号。ＩＦＴ 基本原理如式（６）所示。

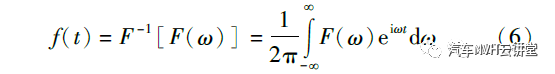
作为初始输入通过计算得到的９ 条传递路径相应的客观参量值及其与总噪声客观参量的对比结果如表３ 所示。

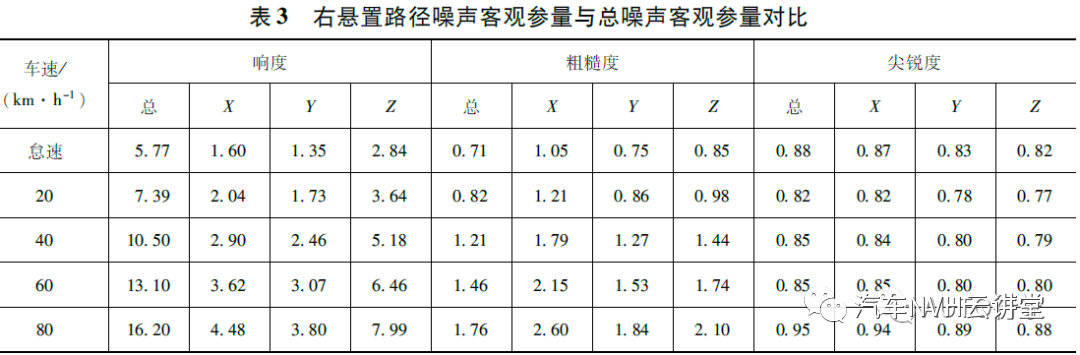
由表可见，与总噪声等于各路径贡献噪声的线性叠加不同，各路径与总的声品质客观参量存在非线性的关系。如右悬置３ 条路径贡献的响度叠加大于总响度，总粗糙度小于右悬置Ｘ 方向路径的粗糙度，本文中通过分析比较各路径对应噪声的频谱分布，确定其为频域掩蔽效应作用的结果。

掩蔽效应分为频域掩蔽和时域掩蔽，频域掩蔽效应是指一个强纯音会掩蔽在其附近同时发声的弱纯音，由于声音频率与掩蔽曲线的非线性关系，为从感知上来统一度量声音频率，引入了临界频带的概念［９］。各个路径合成的噪声在不同频带上存在着相互的干扰，因而在基于临界频带进行声品质客观参量的计算时出现了这种非线性的结果。

３.２ 声品质贡献因子

由于各路径声学参量与总声学参量的关系无法明确描述，且数据较多，分析较为繁琐，为更清晰地反映各路径声品质贡献情况，引入声品质贡献因子（ｓｏｕｎｄ ｑｕａｌｉｔｙ ｃｏｎｔｒｉｂｕｔｉｏｎ ｆａｃｔｏｒ）的概念，其计算公式为

式中：Ｙｉ 为第ｉ 工况下的总烦躁度；Ｙｉｊ为第ｉ 工况下ｊ路径对应的烦躁度。

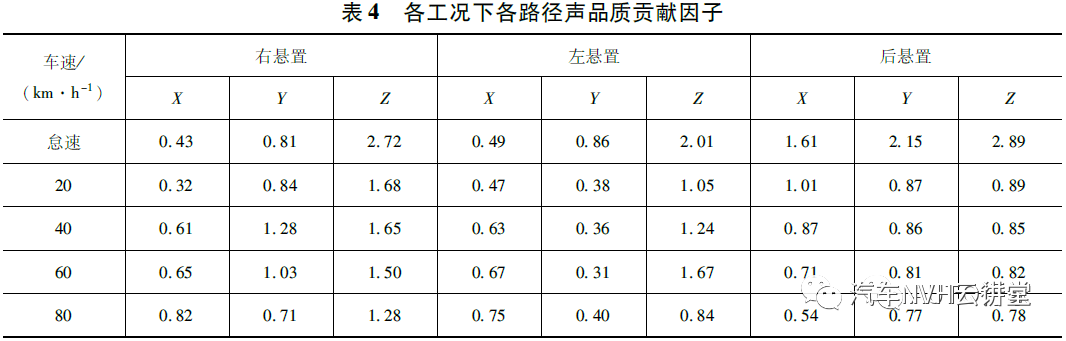
将各工况下各路径合成的响度、粗糙度和尖锐度值输入到前面所建ＧＡ-ＢＰ 声品质预测模型中，获得相应的烦躁度值，进而求得声品质贡献因子，结果如表４ 所示。

由表可见：左右悬置的Ｚ 方向贡献因子均明显大于其他２ 个方向，而后悬置３ 个方向较为均衡；同时，在一些工况下，总烦躁度小于部分结构路径噪声所引起的烦躁度，说明在实验室模拟的平滑路面上，由于声音的掩蔽效应，部分工况下的进排气和发动机表面辐射等路径噪声削弱了发动机振动路径噪声的烦躁度。

考虑到右悬置Ｚ 向的声品质贡献因子在各工况下均较为突出，且明显大于Ｘ、Ｙ 向，可进行有针对性的优化，因此确定右悬置Ｚ 方向作为最主要的烦躁度贡献路径，而对右悬置参数进行优化。

4、发动机悬置优化

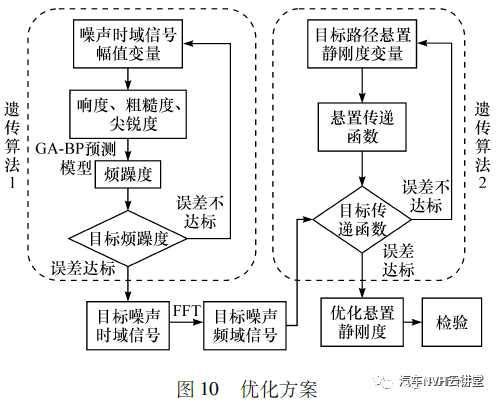
由于优化目标为降低烦躁度而非噪声声压级，不能简单地通过调整悬置参数来降低传递函数某一频段的幅值来实现。为明确优化方向，本文中制定了确定目标烦躁度、搜索目标传递函数、匹配悬置元件参数达到优化目的的两级优化策略，具体操作流程如图１０ 所示。

４.１ 遗传算法

遗传算法是模拟生物遗传和进化过程而建立起来的一种全局寻优算法。由于其不依赖于梯度问题，因而具有较强的鲁棒性，适用于解决传统搜索方法难以解决的复杂非线性问题［１０］。本文中基于遗传算法对非线性问题的全局搜索能力，对悬置参数和传递函数进行优化，以改善车内声品质。

４.２ 悬置路径传递函数优化

考虑到右悬置Ｚ 向路径的烦躁度值在较高车速时数值较大，制定了阶梯型的优化目标，即：怠速工况烦躁度值降低１；２０ 和４０ ｋｍ／ｈ 烦躁度值降低２；６０ 和８０ ｋｍ／ｈ 烦躁度值降低３。根据此目标，以合成的路径噪声信号的时域信号幅值为变量，变化量为－０.１ ～０.１ Ｐａ，将其输入编写的声品质客观参量计算和声品质预测模型，获得相应的烦躁度值，挑选出与优化目标烦躁度值对应的噪声信号。

由于噪声信号与客观参量和客观参量与烦躁度均为非线性关系，须对计算所得多个符合优化目标的噪声信号进行筛选。考虑到结构噪声的影响范围主要集中在中低频段，故以频域信号中低频段（５０ ～５００ Ｈｚ）ＲＭＳ 值最小为目标，利用遗传算法对符合优化目标的噪声信号进行筛选，确定优化后的路径噪声频域信号，进而得到相应的右悬置Ｚ 方向传递函数的优化目标。图１１ 和图１２ 分别为怠速和６０ ｋｍ／ｈ 工况下优化前后右悬置Ｚ 方向所贡献的车内噪声，图１３ 为两工况下所确定的右悬置Ｚ 向目标传递函数。

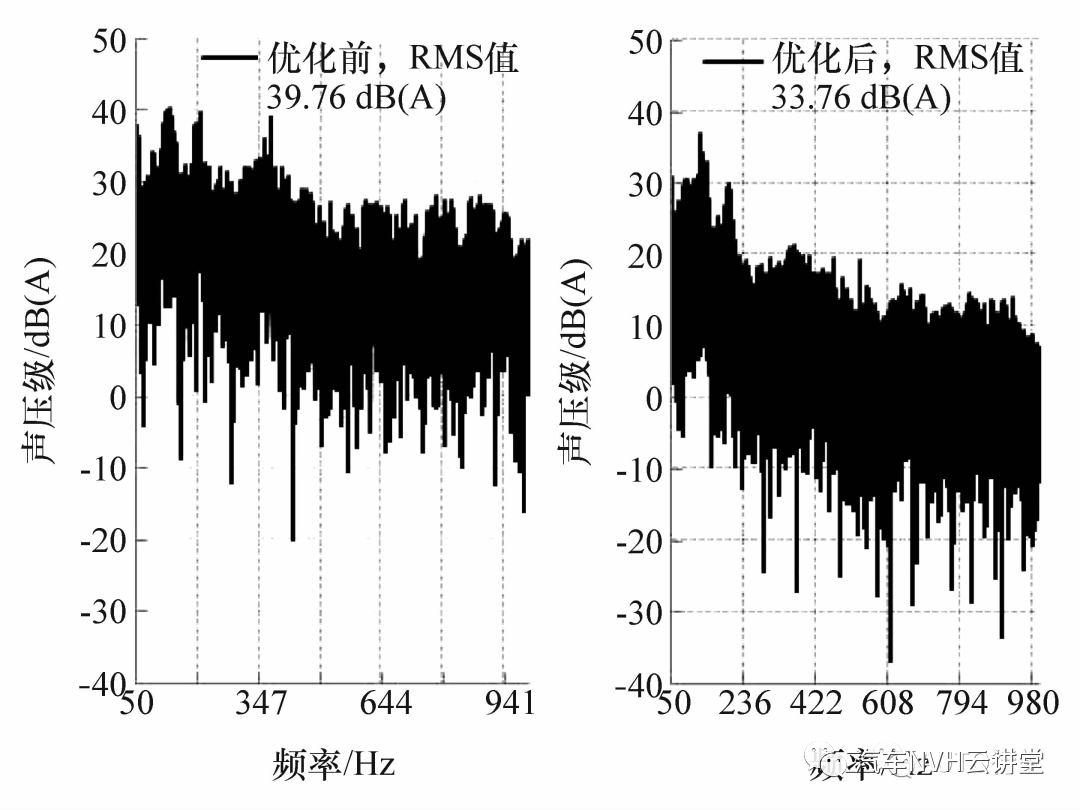
图11怠速工况优化前后右悬置Ｚ 向贡献噪声

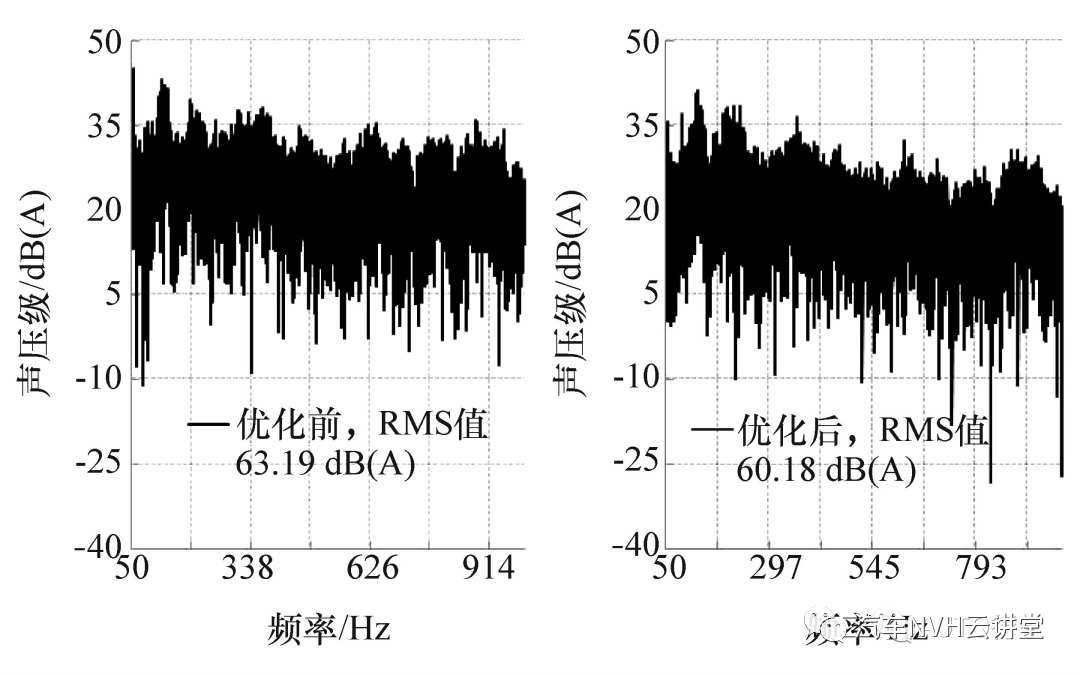
图12 ６０ ｋｍ／ｈ 工况优化前后右悬置Ｚ 向贡献噪声

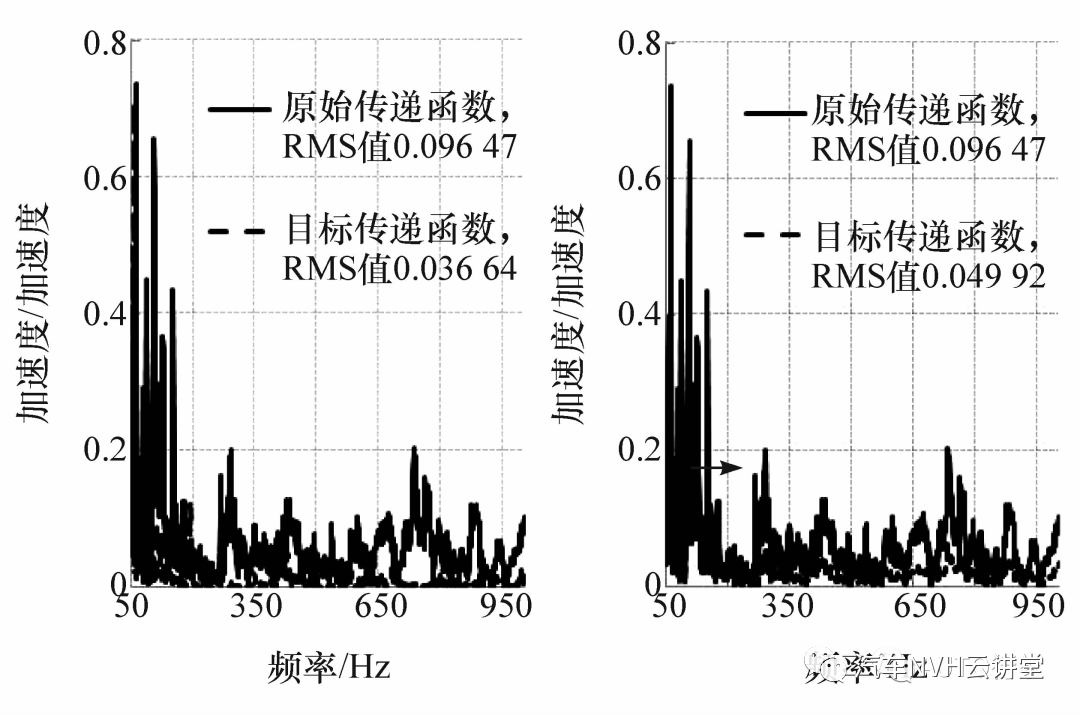
图13 怠速工况（左）和６０ ｋｍ／ｈ 工况（右）传递函数优化目标

由图可见，由于每个工况的优化目标不同，导致优化的传递函数也不相同，而实际上传递函数作为悬置结构的固有属性，不随激励变化而改变，因此下面将在各工况的目标传递函数的基础上进行权重分析，通过悬置参数的优化来获得改善车内声品质最有效的传递函数。

４.３ 悬置参数优化

发动机悬置系统的运动可看作一个由质量、弹簧和阻尼构成的６ 自由度振动模型［１１］，其运动微分方程为

式中：质量矩阵Ｍ 包括发动机质量ｍ、发动机绕Ｘ、Ｙ、Ｚ 轴的转动惯量和惯性积；刚度矩阵Ｋ 包括各悬置元件的静刚度、扭转刚度和相互之间的耦合刚度；阻尼矩阵Ｃ 为各悬置元件的阻尼值。

由式（８）可知，以悬置系统为研究对象时须考虑各悬置元件间的耦合作用，考虑到本文中以改善右悬置Ｚ 向传递函数为目标，因此将右悬置元件单独分析，获得无耦合的悬置元件运动方程，同时忽略对传递函数的影响较小的悬置元件扭转运动和阻尼的调节，以悬置元件的静刚度作为优化控制对象，简化后的右悬置元件运动方程为

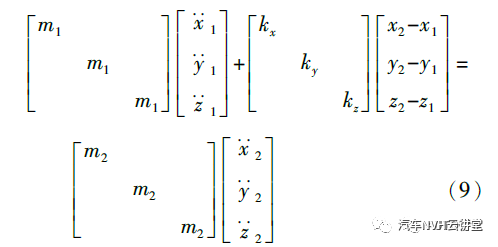
式中：ｍ１ 为发动机质量，ｍ１ ＝１８１ ｋｇ；ｍ２ 为整备质量（１ ４８０ ｋｇ）与ｍ１ 的差值；ｋｘ、ｋｙ、ｋｚ 分别为右悬置３个方向的静刚度；ｘ１ 、ｙ１ 、ｚ１ 和ｘ２、ｙ２、ｚ２ 分别为悬置主被动侧位移。

求解式（９），得到被动端Ｚ 向加速度ａ２ 的通解为

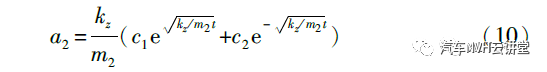
式中：ｃ１ 、ｃ２ 均为常数；ｔ 为采样时间。为便于后续计算，取ｃ２ 为０，将试验采集的ａ２时域信号代入式（１０），可得各采样时刻对应的ｃ１值，进而确定Ｚ 向时域传递函数：

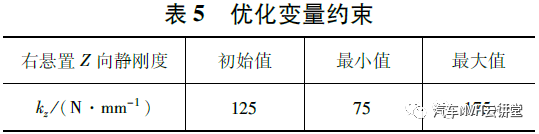
基于式（１１），在Ｍａｔｌａｂ 中编写遗传算法优化程序，其核心适应度函数如图１４ 所示，包括时域传递函数ＦＦＴ 变换，定义变量为右悬置Ｚ 向的静刚度ｋｚ，定义适应度目标为Ｚ 向传递函数０ ～１ ０００ Ｈｚ 的ＲＭＳ 值与目标传递函数的ＲＭＳ 值的相对误差最小。考虑到样车内部布置空间的限制和对悬置系统固有频率的控制，对优化变量的范围进行了约束，如表５所示。

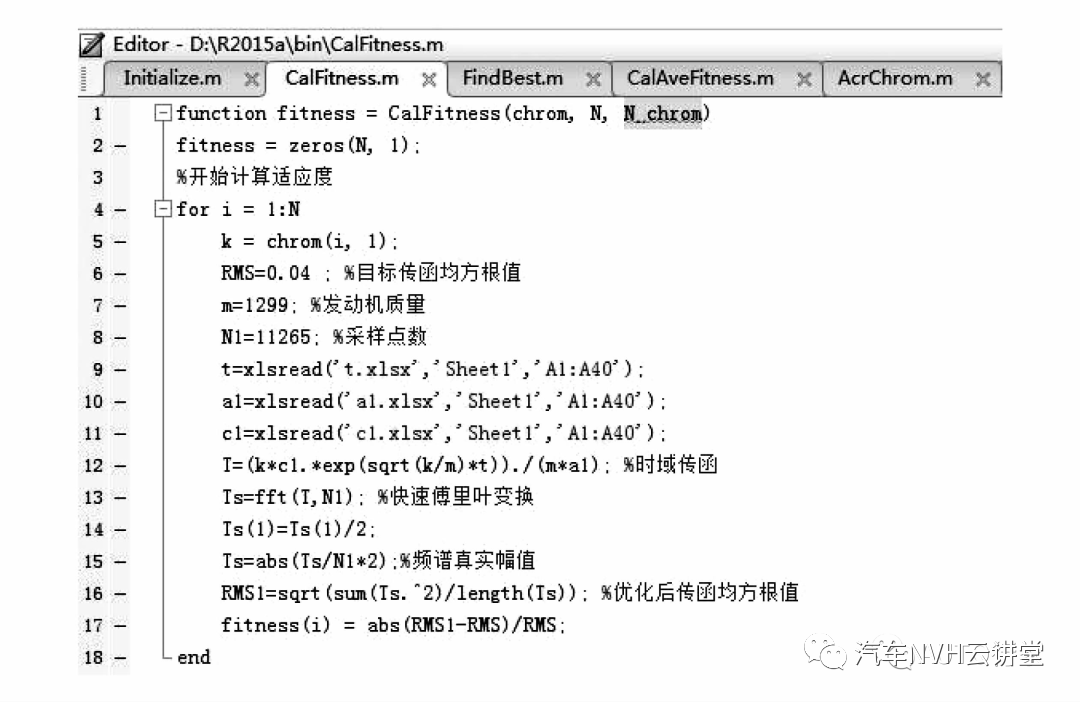
图14 遗传算法适应度函数

由于每个工况的目标传递函数并不相同，通过仿真计算，获得了５ 个优化ｋｚ值及其对应的传递函数，如表６ 所示。图１５ 为６０ ｋｍ／ｈ 工况下优化结果与目标传递函数和原始传递函数的对比。由图可见，优化结果在２００ Ｈｚ 以下要优于目标传递函数，在２００ ～１ ０００ Ｈｚ 两者基本一致，优化结果略高，ＲＭＳ 值相对误差为２.１％，说明优化程序具有较高的准确性和有效性。

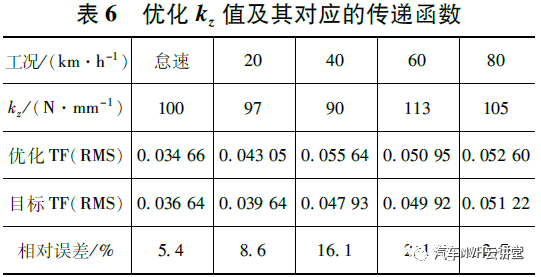
在传递函数的最终选择上，首先排除误差较大的４０ ｋｍ／ｈ 工况ｋｚ 值，同时考虑到右悬置Ｚ 向声品质贡献因子最大的怠速工况在实际生活中持续的时间较短，而与８０ ｋｍ／ｈ 工况相比，较常用的６０ ｋｍ／ｈ的声品质贡献因子较大，且优化后的传递函数优于８０ ｋｍ／ｈ，故选取６０ ｋｍ／ｈ 工况优化所得的ｋｚ 值和传递函数作为最终的优化结果。

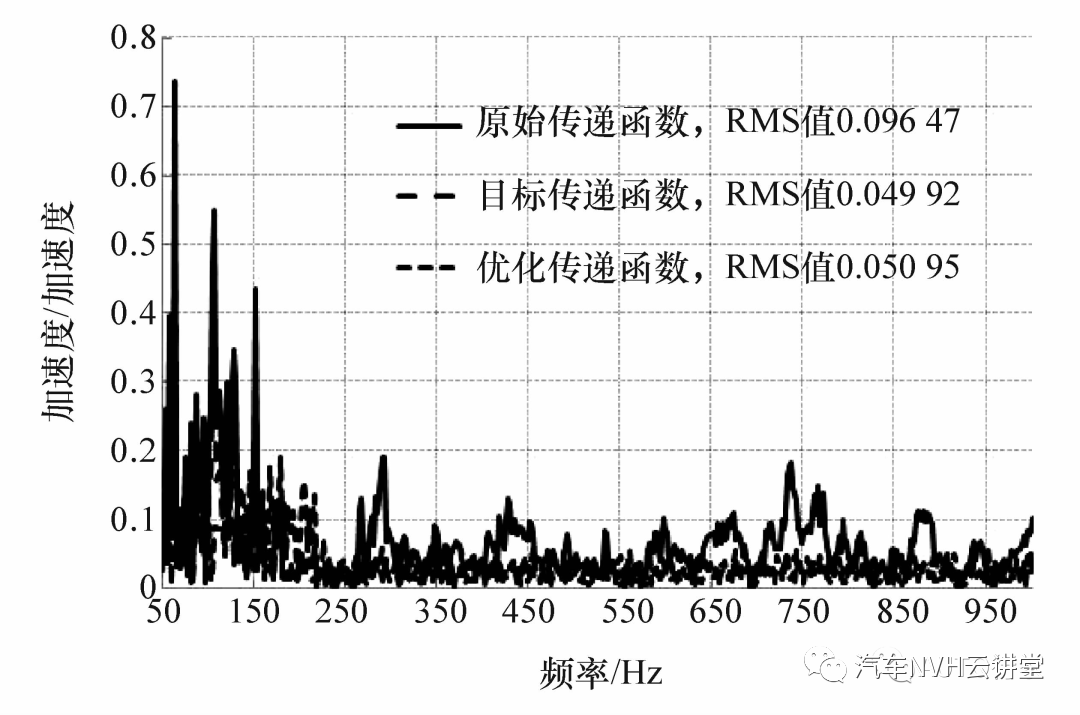
图１５ ６０ ｋｍ／ｈ 工况优化传递函数

间较短，而与８０ ｋｍ／ｈ 工况相比，较常用的６０ ｋｍ／ｈ的声品质贡献因子较大，且优化后的传递函数优于８０ ｋｍ／ｈ，故选取６０ ｋｍ／ｈ 工况优化所得的ｋｚ 值和传递函数作为最终的优化结果。

４.４ 优化效果检验

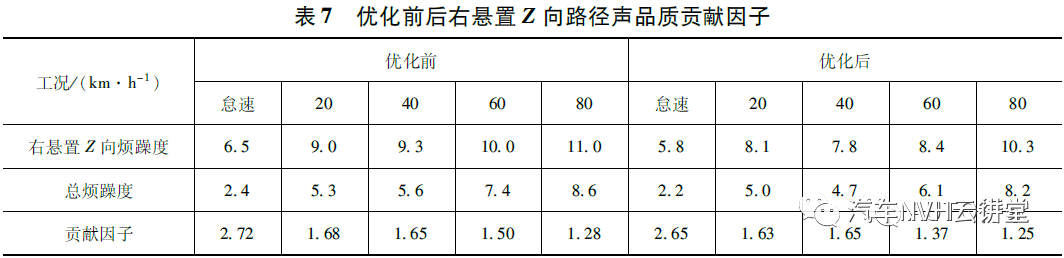
为检验优化效果，将优化后的传递函数代入右悬置Ｚ 向路径对应的车内噪声和响度、尖锐度、粗糙度的计算中，将结果输入ＧＡ-ＢＰ 烦躁度预测模型，得到新的总烦躁度值和右悬置Ｚ 向路径声品质贡献因子，如表７ 所示。由表可见：通过优化控制声品质贡献因子较大的右悬置Ｚ 向路径传递函数，有效地降低了车内总噪声所引起的烦躁度；同时，右悬置Ｚ 向的贡献因子也有所降低，说明传递函数的优化减弱了该路径对总烦躁度的影响。通过检验，证明优化方案取得了较好的效果。

5、结论

（１）通过传递函数测试和ＴＰＡ 合成计算，确定了发动机３ 个悬置Ｘ、Ｙ、Ｚ 方向共９ 条具有较高精度的结构噪声传递路径，可用于声品质贡献分析；

（２）基于声品质客观参量计算和主观评价，利用遗传算法和神经网络建立了声品质预测模型，通过声品质贡献因子计算，直观地反映了结构噪声传递路径对烦躁度的贡献情况和声音掩蔽效应对声品质的作用，得出右悬置Ｚ 向路径对烦躁度影响较大，并确定了对该路径对应烦躁度的优化目标；

（３）制定两级优化方案，先通过遗传算法搜索与目标烦躁度相对应的右悬置Ｚ 向传递函数，再通过遗传算法匹配右悬置Ｚ 向静刚度并加以检验。结果表明，通过两级优化获得的右悬置Ｚ 向静刚度及其传递函数有效地降低了车内总噪声所引起的烦躁度，提高了车内声品质，证明本文中所制定的研究内ＩＳＯ-Ａ／Ｃ 级路面激励工况下Ｔ-Ｓ 观测器车辆侧倾状态估计结果的对比，有效验证了ＵＫＦ＆Ｔ-Ｓ 算法的有效性，且与ＣａｒＳｉｍ© 仿真数据相比识别状态标准偏差不超过１０％。

作者：曾发林１ ，胡 枫２

单位：１.江苏大学汽车工程研究院 ２.江苏大学汽车与交通工程学院

来源：汽车工程