汽车动力总成悬置系统对整车启动工况的影响

摘要：为解决某新开发SUV的整车启动振动大的问题，该文根据对动力总成悬置系统弹性轴与扭矩轴的理论分析，运用ADAMS软件建立了整车刚柔耦合仿真模型，利用MATLAB编程提取启动瞬态激励并加载到模型里进行仿真，经与试验数据对比，仿真精度达到90％以上，准确地预测出悬置系统刚度对整车启动振动的影响。通过优化悬置刚度，车内振动降低了50％，使启动振动得到了有效控制，该方法的建立为控制整车启动振动提供了新思路。

关键词：汽车动力总成；悬置系统；启动工况；弹性轴；扭矩轴汽车在启动、怠速及加速行驶等各种工况下良好的平顺性和低噪声是评判现代汽车质量优劣的重要标志11I。悬置系统除了支撑动力总成和限制动力总成的位移外，还要隔离发动机和路面在不同工况下的振动。这就要求悬置的刚度不仅要满足小振幅工况下的隔振，还要满足大振幅工况下的限位作用。目前，国内外学者通常采用能量解耦法及动力总成悬置系统的模态频率分布为优化目标，主要针对怠速工况进行优化设计，对启动过程中悬置系统的影响研究很少。文章运用MSCADAMS建立刚柔耦合的仿真模型，根据发动机启动过程中的缸压变化模拟启动激励，通过仿真分析与试验结果的对比，验证了模型的仿真精度，并总结出横置动力总成悬置系统对整车启动工况的影响规律。

1 理论分析发动机的启动过程是较为复杂的瞬态过程，在整个过程中动力总成产生较大的扭矩波动。从振动机理上分析，启动振动问题是由动力总成的波动，经悬置系统传递到车身的过程，因此悬置对启动振动的抑制及隔离非常重要。若不考虑悬置系统的支撑，动力总成在启动激励的作用下会沿某一固定的轴转动，该轴的位置是由动力总成本身的质量及惯性参数决定I引，称之为扭矩轴，动力总成关于扭矩轴的位移响应表达式，如式(1)所示。

 (式中：HTRA——动力总成关于扭矩轴的位移响应，mm；M一系统的质量矩阵；ω——频率，Hz；fTA——沿曲轴方向的单位扭矩激励向量，N·m。若忽略动力总成本身参数的影响，只对悬置系统进行研究，在启动激励的作用下，由悬置系统支撑的无质量动力总成会绕弹性轴转动，该轴的位置由悬置布置位置、角度及刚度决定，动力总成关于弹性轴的运动响应表达式，如式(2)所示。

式中：HEA——动力总成关于弹性轴的位移响应，mm；[K]悬置系统的刚度矩阵。而实际的启动过程中，动力总成受到悬置系统的约束，其表现出的响应是2个轴共同作用的结果，其关系表达式，如式(3)所示。

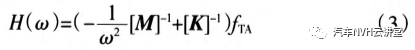
式中：日——实际工况下动力总成的位移响应，mm。由式(3)分析可知，为了能在传递路径上最大限度地抑制或隔离启动激励，需要将悬置系统的弹性轴位置与动力总成的扭矩轴位置重合，但由于悬置的刚度与激振频率及振幅有关删，因此启动过程中弹性轴的位置是随悬置刚度不断变化的，用定频和定振幅下的悬置刚度计算出的弹性轴已不适用于启动振动的分析。在横置动力总成三点式悬置系统设计时，一般考虑在XY平面上，将左右悬置布置与扭矩轴重合，且左右悬置位于扭矩轴的上方、后拉杆位于下方，因此在启动过程中，左右悬置受到的激励振幅较小，而后拉杆悬置主要在x向起到抗扭的作用，受到的激励振幅较大。动力总成启动过程中，悬置处于低频大振幅振动状态，所以用低频大振幅下的刚度计算弹性轴方向更贴合实际工况。但为了能较简便的预测出悬置系统对启动激励的影响，对启动至怠速工况下悬置刚度做以下简化：由于悬置刚度的幅变及频变特性，在启动过程中，静刚度可以作为悬置刚度下限值，频率为25Hz和振幅为±0．1mm(怠速激励)的动刚度可以作为悬置刚度上限值，启动过程中悬置刚度的变化范围必定处于上下限刚度之间。因此针对启动激励，同时考虑动静刚度对弹性轴方向的影响，并控制悬置系统x向刚度的动静比，理论上是可以获得较好的启动振动。2 仿真模型的建立在MSCADAMS里建立刚柔耦合的仿真模型时，将动力总成视为刚体，用形状简单的长方体模拟，通过悬置与车身连接。悬置元件简化为无质量、无扭转刚度和阻尼的弹性单元，为了能够准确地描述橡胶悬置的特性，用ADAMS自带的Bushing模拟悬置。利用有限元分析软件生成的模态中性文件建立车身柔性体模型，车身被动侧通过4个Bushing单元与大地连接，由于悬架实际的横向与纵向刚度较大，将以上4个Bush—ing横向刚度与纵向刚度取值为垂向刚度的90倍。将动力总成和悬置刚度参数输入到模型中，建立悬置系统刚柔耦合仿真分析模型，如图1所示。

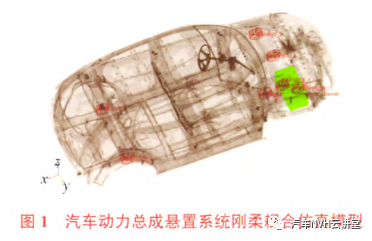
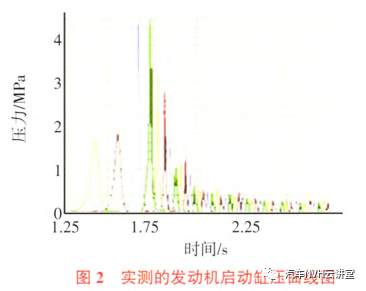
3 启动激励的模拟发动机启动振动是较为复杂的瞬态过程，与发动机电喷控制策略有关，有许多研究人员对此做过详细的分析，并总结出活塞初始位置、冷却液温度及电机拖动转速对启动过程的影响规律【6】，但最重要的影响因素还是缸内气体压力产生的发动机运行阻力矩。由于启动工况的缸内压力和转速等物理量均是瞬态变化的，很难用数学表达式准确地进行描述，因此，需采集实际的发动机启动缸压，并转化为启动激励，具体过程为：1)采集启动过程发动机缸内压力，如图2所示；2)在MATLAB里编写缸压转化程序，部分程序内容，如图3所示；3)模拟得到便于加载到ADMAS的启动扭矩曲线，如图4所示。

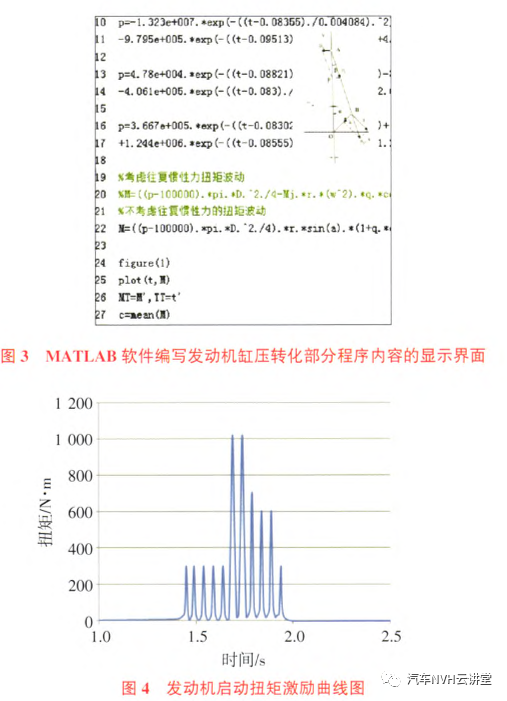
4 实例验证4．1项目背景某款新开发SUV的横置动力总成，在悬置匹配中存在启动时车内振动大的问题，对该车进行悬置被动侧和车内座椅振动测试，测试结果如图5所示。

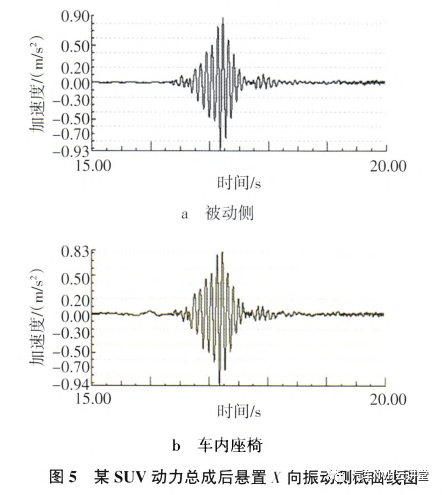
通过多次试验测试，该车启动时车内振动最大峰值平均为0．94m／s2，主观感受启动振动大且时间较长，经过对试验数据分析，发现悬置被动侧x向振动与车内座椅启动振动有较强的相关性，所以主要从悬置上进行启动振动的优化。4．2仿真分析在对启动工况仿真时，对该车型进行启动缸压测试，经转换模拟之后得到启动激励曲线(图4)。设置仿真时间为5s，步长为10000，分别用悬置动刚度和静刚度来计算后悬置被动侧加速度响应'冈0度参数设置，如表1所示.

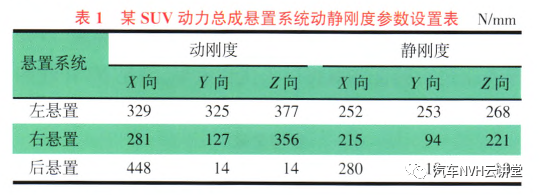
2．1动刚度仿真分析对悬置系统用动刚度进行仿真计算，得到车内振动加速度为0．46m／s2，系统的弹性轴与扭矩轴距离为2．45mm，如图6和图7所示。从图7可知，弹性轴与扭矩轴的距离已经非常接近，得出的车内振动响应也较小，说明动刚度的设计比较合理。

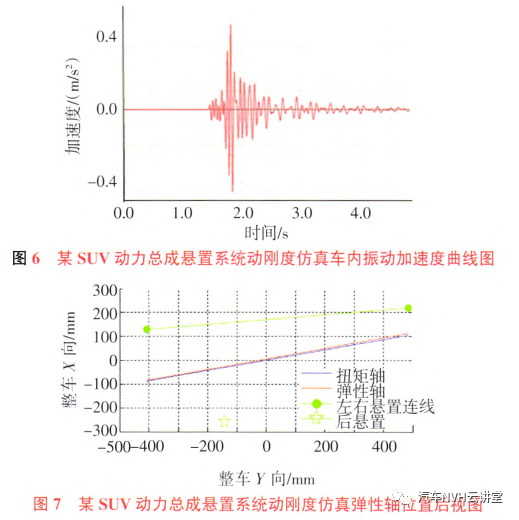
2．2静刚度仿真分析 对悬置系统用静刚度进行计算，得到车内振动加速度为0．93m／s2，系统的弹性轴与扭矩轴距离为36．74mm，如图8和图9所示。从图9可知，静刚度下的弹性轴位置偏上，与扭矩轴的距离较远，得出的车内振动响应较大。

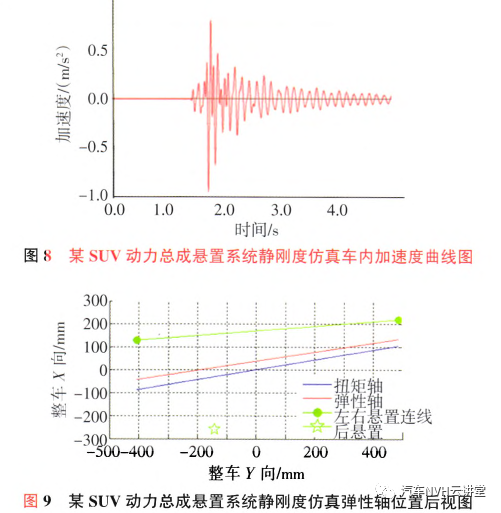
由以上分析结果并结合试验数据，可以得出：1)用悬置静刚度仿真计算得出的启动振动与试验结果比较吻合；2)悬置系统弹性轴与扭矩轴的距离会影响启动振动的峰值大小。因此，为了解决该车型启动时车内振动大的问题，主要优化静刚度下的弹性轴，使其尽量靠近扭矩轴。从图9可以看出，弹性轴的位置主要由悬置系统的x向刚度决定，当某个悬置的x向刚度变大时，弹性轴就会偏向这个悬置。对图9所示的弹性轴位置优化如下。1)增大后拉杆x向刚度使弹性轴靠近扭矩轴，经试验测试，车内启动振动稍有改善，但由于悬置刚度提高，动力总成模态变大，怠速工况悬置隔振变差；2)降低左右x向悬置刚度使弹性轴靠近扭矩轴，经试验测试，车内启动振动加速度由原来的0．94m／s2降低到o．47m／s2，而且对怠速工况影响不大。综合考虑对怠速工况的影响，选取降低左右悬置x向刚度的方法来改善该车型的启动振动大的问题。优化后的结果也是利用文章提出的方法进行仿真计算的，所以此处不再进行详细阐述。优化前后的结果对比，如表2所示。

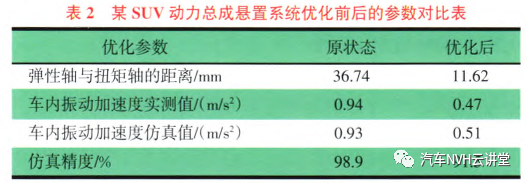
随着左右悬置x向静刚度的降低，弹性轴与扭矩轴的距离变小，使整车启动时的车内响应从原来的0．94m／s2降低到0．47m／s2，降幅达到50％，主观感受改善明显。另外，仿真精度达到了90％以上，证明该仿真模型及方法的准确性。5 结论文章从改变悬置系统弹性轴位置的思路出发，通过调整悬置刚度，成功地解决了整车启动振动大的问题。有许多文献已总结出弹性轴与扭矩轴理论在整车怠速振动控制中的应用效果，文章验证了该理论也可以应用到整车启动振动控制中，并且通过搭建精确的仿真模型预测出整车启动振动的大小，使启动问题在项目开发前期就能通过悬置系统设计进行有效控制。作者：赵珂，鲍金龙等作者单位：长城汽车股份有限公司

来源：汽车工程师