基于混合域优化控制的智能网联车辆运动规划模型

胡笳

李氏基金会杰出成就奖获得者，国家特聘青年专家，上海市东方学者，现任同济大学交通运输工程学院教授/博导，曾任美国交通部联邦公路局（FHWA）研究所副研究员。目前担任IEEE Transaction on Intelligent Vehicles副主编、IEEE Open Journal of Intelligent Transportation Systems副主编、ASCE Journal of Transportation Engineering, Part A: Systems副主编以及多个期刊的助理主编；任美国科学院TRB自动驾驶委员会委员、高速公路管理委员会、美国土木工程学会先进科技委员会委员、美国土木工程学会可持续交通委员会委员、美国土木工程学会人工智能委员会委员、中国汽车工程学会汽车智能交通分委会副秘书长、中国人工智能学会智能驾驶专委会委员、中国自动化学会预测控制与智能决策专委会委员，以及中国公路学会自动驾驶委员会委员。

0

引 言

据统计，2015年我国发生道路交通事故187781起，造成25万人以上伤亡，其中94%的道路交通事故都与驾驶员错误操作有关。智能网联车辆具备自主决策控制能力，能够规避驾驶员错误操作，从而减少交通事故，保障驾驶安全。

作为智能网联车辆决策控制的重要一环，运动规划（Motion Planning）以追踪参考路径为目标，规划车辆具体运动轨迹或直接输出底层控制指令。运动规划对于智能网联车辆运行效率、安全、能耗具有显著影响。传统运动规划模型以规划运动轨迹为目标，以图搜法为代表，具有如下缺陷：①只能规划车辆轨迹，难以产生速度、加速度、方向盘转角等车辆底层控制指令，从而对车辆底层反馈控制提出更高的要求；②无法考虑车辆动力学特性，从而导致规划轨迹存在无法被车辆执行的问题，这会降低控制精度并带来潜在安全风险；③图搜法单以效率为目标，难以适用舒适、节能等多目标驱动的运动规划。

为了解决传统图搜法的缺陷，学者提出了基于优化控制的运动规划方法。相较于图搜法，优化控制法能够规划运动轨迹并输出车辆加速度、方向盘转角等底层控制指令。优化控制法主要包括两类方法：人工智能方法和基于模型的方法。基于人工智能方法的运动规划模型易于建立，但是对数据需求量较大，训练数据往往难以覆盖长尾场景。当前基于模型的优化控制方法存在以下缺陷：①控制精度难以保证，且大多未得到充分的实车验证。②无法保证求解效率。基于模型的优化控制方法存在PSPACE-hard问题，传统方法采用二次规划求解器进行求解，求解效率较低。③车辆模型不够精确，未考虑车辆执行延迟、转向系统动态。车辆方向盘转角控制和加速度控制均存在0.3s左右时延，缺乏对执行延迟的考虑将显著降低控制精度。

针对以上缺陷，本文提出一种基于优化控制的运动规划模型，具有以下特性：

(1) 基于时空混合域建模：纵向控制基于时间域建模，横向控制基于空间域建模。横向控制以在某一纵向位置时到达特定横向位置为目标，从而避免横向控制中掺杂纵向控制误差，提高运动规划模型循迹精度。

(2) 基于动态规划原理的求解算法：提高求解效率，保证实车测试中平均求解时间为5.15毫秒。

(3) 考虑车辆底层控制时延、转向传动系统动态，并对其进行实车测试标定。

(4)实车测试验证该运动规划模型有较好控制精度：在60 km/h以下的复合场景中，循迹精度在12.5cm以内。

1

研究范围

本文提出的运动规划模型应用于图1所示的智能网联车辆决策控制系统，该系统包括如下四个子模块：

（1）行为决策：该模块接收传感器收集的环境感知信息以及车辆底层线控提供的车辆状态信息，进而规划决策车辆驾驶行为，如跟驰、换道、超车等。

（2）路径规划：路径规划模块接收上层行为指令，依据车辆当前状态及环境状态，规划车辆实现目标行为的参考路径。

（3）运动规划：运动规划以追踪参考路径为目标，规划车辆底层控制指令，包括车辆期望方向盘转角和期望加速度。

（4）底层执行：该模块接收、执行运动规划所输出的控制指令，并反馈实时车辆状态。

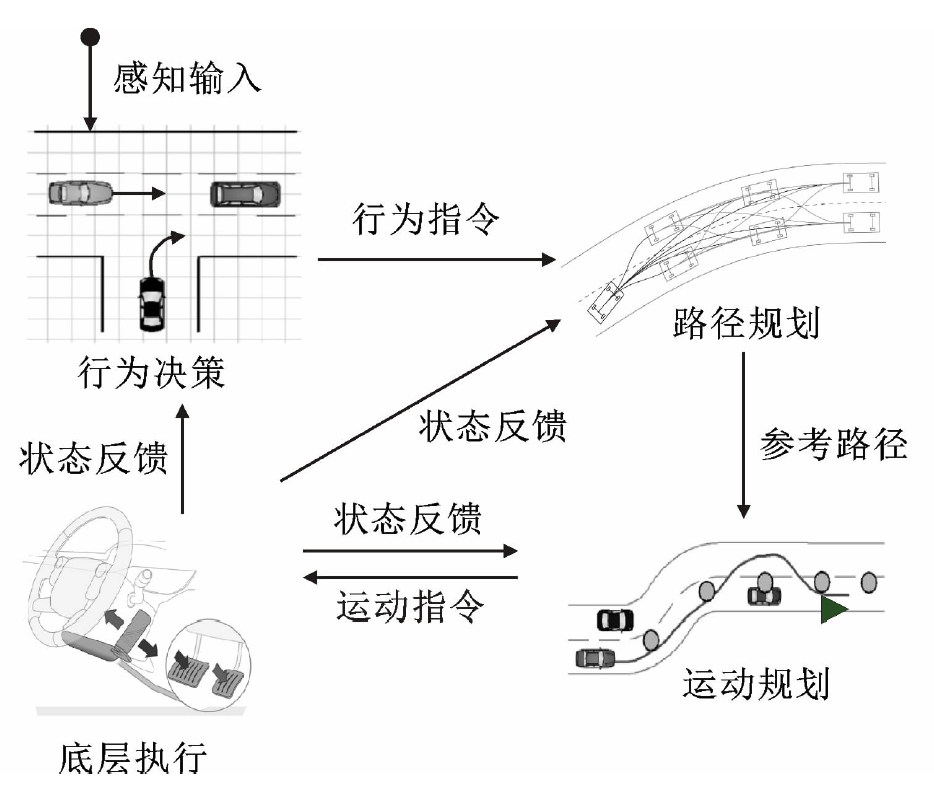
图1智能网联车辆决策控制系统架构

本文聚焦于图1所示系统中的运动规划模块，所提出的智能网联车辆运动规划模型包括纵向运动规划模型和横向运动规划模型。以追踪参考路径为目标，纵向运动规划模型输出车辆期望加速度，横向运动规划模型基于纵向规划轨迹，输出车辆期望方向盘转角。

2

运动规划模型建立

作为一种基于模型的优化控制方法，模型预测控制（Model Predictive Control）近年来逐步被应用于智能网联车辆决策控制领域。本文基于模型预测控制架构，将车辆运动进行纵横向解耦，分别建立车辆纵向、横向运动规划模型，改进并优化车辆动力学模型。

2.1 模型定义

在图1所示智能网联车辆决策控制系统中，路径规划模块输出的参考路径包括车辆空间位置坐标点以及到达该坐标点的速度、时间信息。车辆运动规划模型接收参考路径信息，以追踪参考路径为目标，输出加速度、方向盘转角到车辆底层执行模块。为更好匹配车辆循迹这一目标，本研究中的运动规划模型建立于参考路径坐标系，如图2所示，其中纵向（X轴方向）为沿参考路径方向；横向（Y轴方向）为垂直参考路径方向。

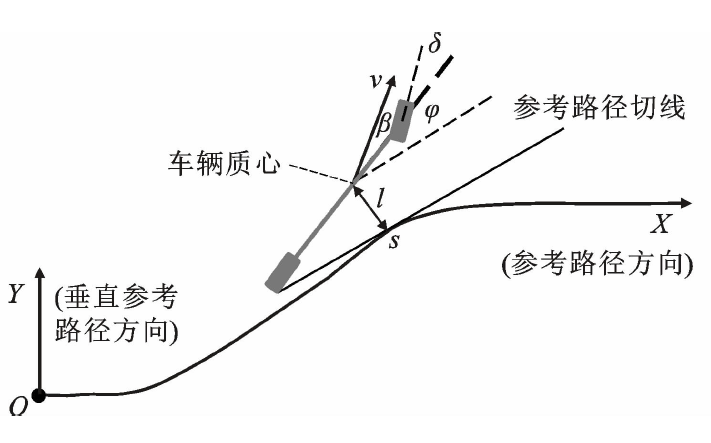
图2参考路径坐标系下符号示意图

为提高循迹精度，本文提出的运动规划模型基于时空混合域建模，即纵向规划基于时间域、横向规划基于空间域。在时空混合域中，车辆循迹目标为在某一纵向位置时到达某一横向位置。而传统时间域建模方法中，车辆循迹目标为在某一时刻同时到达某一纵向以及横向位置。因此，基于混合域的建模方法能够解耦车辆纵横向循迹误差，从而提高循迹精度。

在参考路径坐标系下，本小节建立车辆纵向状态量、纵向控制量、横向状态量、横向控制量如下：

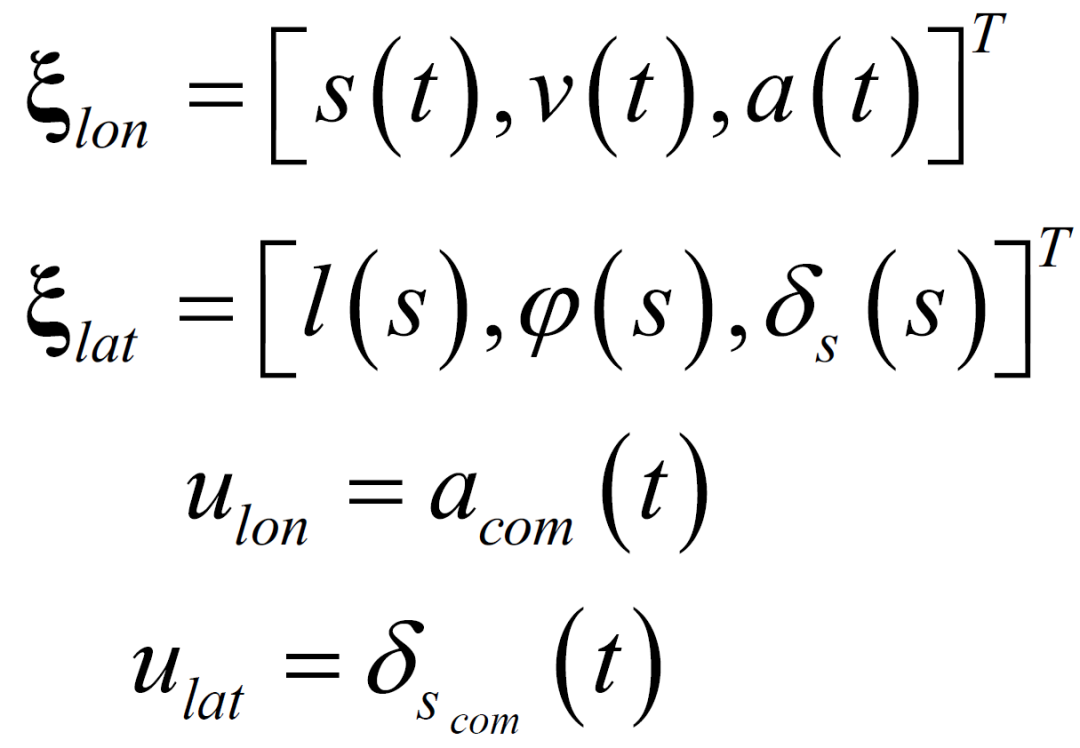
其中，变量定义如图2所示。

为了实现最小化循迹误差的控制目标，参考路径坐标系下车辆纵向目标状态和横向目标状态定义如下：

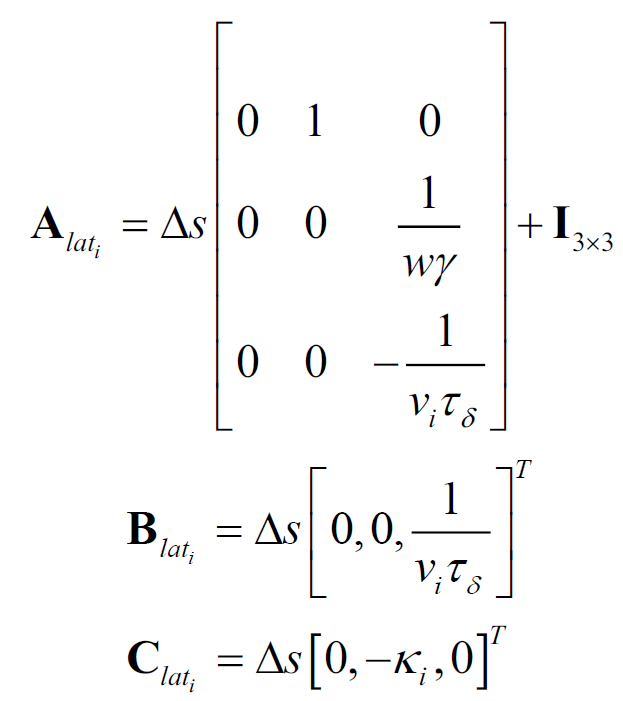
2.2 混合域车辆动力学模型

在基于优化控制的车辆运动规划方法中，车辆动力学模型反映了车辆状态量和控制量的递推关系，是优化控制理论的系统动态模型。本文建立了面向时空混合域、考虑车辆执行延迟以及转向系统动态的车辆动力学模型，如定理 1所示。

定理1：时空混合域下车辆横、纵向动力学模型如下：

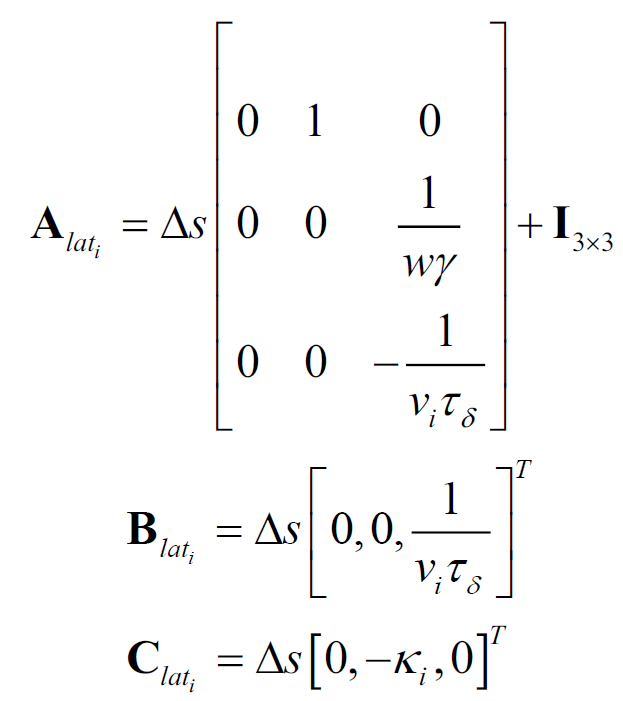
其中：

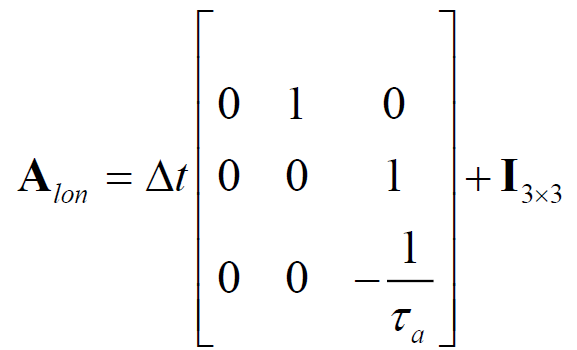
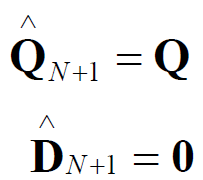
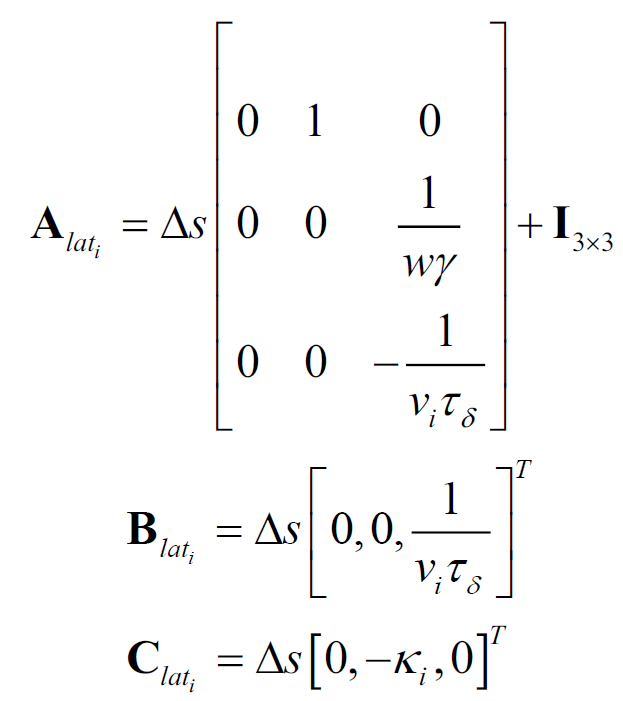
该模型基于传统自行车模型，并进行线性化、混合域转化、离散化，并考虑转向传动系统动态、车辆执行时延。其中，γ是车辆转向传动比。由于本文采用自行车模型对车辆进行建模，无法精确刻画阿克曼转向关系。且由于前文所述小转角假设的存在，不同速度下自行车模型车辆前轮偏角和实际方向盘转角之间非线性关系。本文采用分段线性化的方法，基于吉利博瑞实车测试，标定其取值如下表。

表1车辆转向传动比取值表

2.3 运动规划模型

为了实现追踪参考路径的目标，本文所提出的运动规划模型以最小化状态量误差为目标，并均衡考虑控制成本。因此，其成本函数可建为状态量误差平方与控制量平方之和的二次型形式。

纵向运动规划模型：

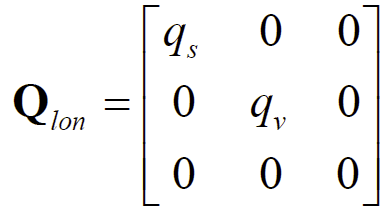
其中，Qlon为纵向权重系数矩阵，qs为纵向位置误差权重系数，qv为纵向速度误差权重系数。rlon为加速度成本权重系数。通过调节q、r的大小，能够权衡循迹精度、行驶舒适性、燃油经济性等多目标。例如提高qs，能提高位置误差在成本函数中的占比，位置误差增加会极大提高整体成本，因此运动规划方案将加快循迹位置误差收敛。又如，提高rlon将提高加速度成本在成本函数中的占比，有利于降低循迹误差波动。

横向运动规划模型：

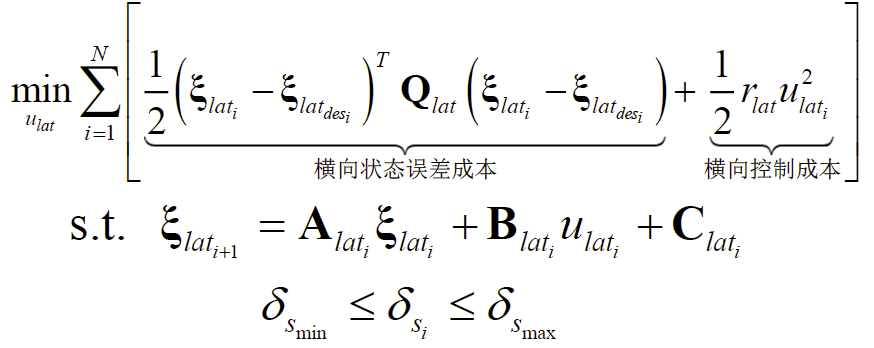
3

求解算法

本文提出的运动规划模型基于前序研究中的动态规划求解算法，将优化控制问题转化为多个重叠子问题，只需逐步求解每步的优化子问题即可，从而提高求解效率。针对本文时空混合域下的车辆运动规划问题，求解算法如下：

步骤1：输入车辆模型中的A、B、C参数矩阵，成本函数中Q、R权重系数矩阵以及初始状态、期望状态，对应计算x(i)以控制步数N

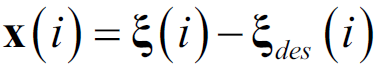
步骤2：对于末态i=N+1：

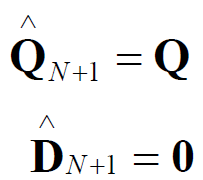
步骤2：for i from N to 1，计算系数矩阵：

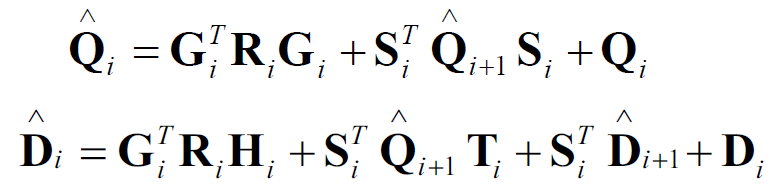
其中，

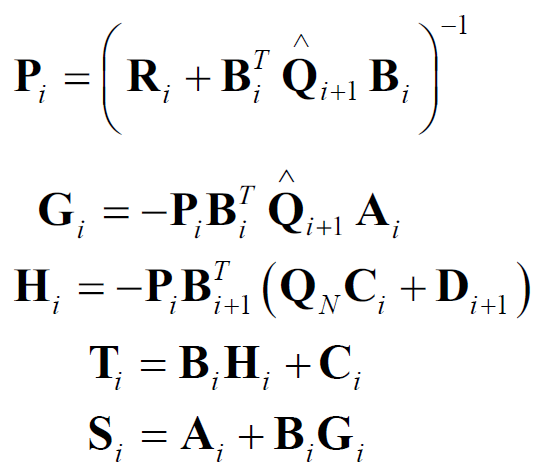
步骤3：for i from 1 to N，计算控制律：

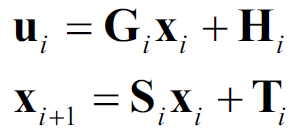
4

仿真与实车验证

本文所提出的运动规划模型通过仿真验证、实车测试两种方法进行验证评估。评估指标为模型循迹精度，包括纵向速度误差与横向位置误差。

4.1 仿真实验设计

仿真架构如图3所示，仿真验证以MATLAB/Simulink为实时仿真环境，基于PreScan搭建仿真场景，以车道中心线为参考路径输入到本文所提出的运动规划模型。运动规划模型规划车辆加速度、方向盘转角运动指令，并输出到Carsim提供的系统模拟车辆行为的参数化仿真车辆进行执行，车辆行为将展示在PreScan场景中。

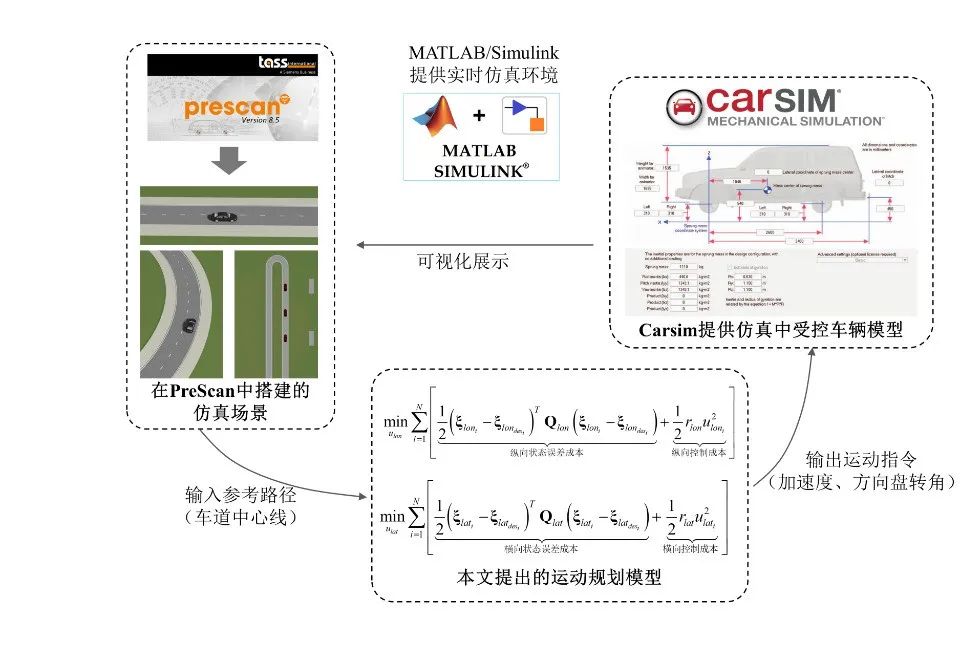
图3 仿真架构

其中，仿真场景包括直线巡航换道、曲线巡航、U-turn：

• 场景1：直线巡航换道，期望速度30km/h。

• 场景2：曲线巡航，转弯半径150 m，期望速度12~13 km/h。

• 场景3：U-turn，转弯半径20 m，期望速度10 km/h。

4.2 仿真测试结果

本文所提出的运动规划模型在仿真测试中展现出较好的控制精度。如图4、图5、图6所示，本文提出的运动规划模型在直线换道、曲线巡航、U-turn这三种场景下循迹精度均较好，循迹误差均在9 cm以下，速度误差在0.7 km/h以下。具体地，如图4所示，在直线换道场景中，最大横向误差为2.52 cm，最大速度误差为0.66km/h。如图5所示，在曲线巡航场景中，最大横向误差为2.65 cm，最大速度误差为0.65km/h。如图6所示，在U-turn场景中，最大横向误差为8.76 cm，最大速度误差为0.57km/h。

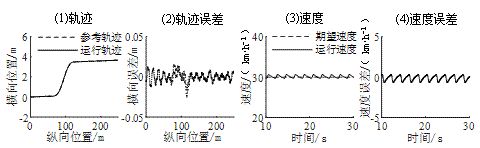
图4仿真测试结果：场景1（直线巡航换道）

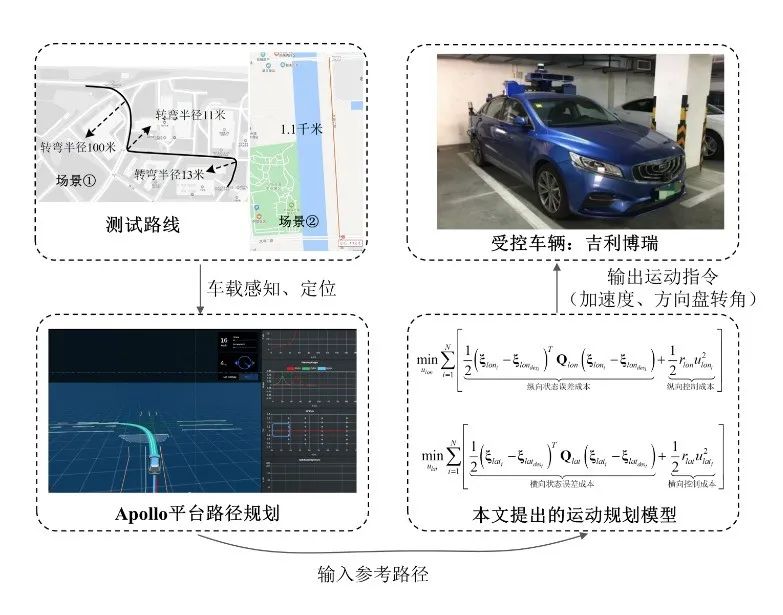
图5仿真测试结果：场景2（曲线巡航）

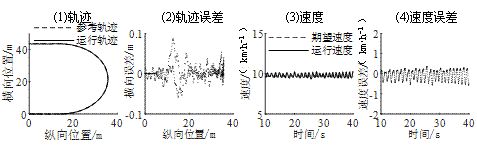
图6 仿真测试结果：场景3（U-turn）

4.3 实车测试设计

实车测试架构如图7所示，由Apollo平台进行感知、定位、决策以及路径规划，将参考路径输入到本文所提出的运动规划模型。运动规划模型规划并输出加速度、方向盘转角指令到测试车辆进行执行。

图7 实车测试架构

实车测试场景如图7所示，场景①全长650 m，包含直行、换道、交叉口转弯、曲线巡航等多个场景。在这条路线上，实车测试了10 km/h、20km/h、30km/h、40km/h、50km/h的期望速度下的循迹精度。场景②为开放道路直线场景，实车测试了运动规划模型在50~60km/h期望速度下的控制效果。

4.4 实车测试结果

本文所提出的运动规划模型的实车测试轨迹如下：

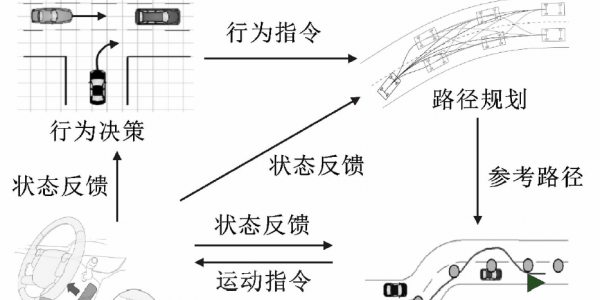
图8 实车测试UTM坐标轨迹

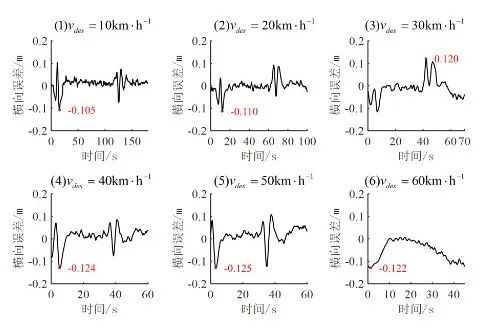
实车测试循迹精度如图9所示，其中直线部分循迹精度较高，误差均在5 cm以内。交叉口转弯处循迹误差最大，最大循迹误差为12.5 cm，发生在期望速度50 km/h下的左转场景中。在Xu等人于2019年发表在IEEE Transactions on Intelligent Transportation Systems的文章中，其提出的运动规划模型在M-city进行了实车测试，该测试仅涵盖期望速度20km/h的直行、半径小于15 m的弯道场景，其测试结果显示车辆最大循迹误差为15 cm。如图9 (2)所示，本文所提出的车辆运动规划模型在20 km/h期望速度下，最大循迹误差为11 cm，相较前人研究降低了27%。此外，本文所提出的车辆运动规划模型经过了60km/h以下速度区间的测试，均能够保证循迹误差在12.5 cm以下。这说明本文所提出的运动规划模型的循迹精度相较国际领先水平有较为显著的提高。

平均循迹精度如表3所示，在10 km/h至50 km/h期望速度下包含直线、弯道、交叉口转弯场景的测试中，随着期望速度的增加，平均循迹误差缓慢增加，但均小于3.5 cm，说明本文提出的运动规划模型具有较高的循迹精度。而60 km/h期望速度下的测试由于测试条件的限制，仅覆盖直线场景，因此60 km/h期望速度下的平均循迹误差相较其他速度明显更低，仅为0.41cm，这也反应了本文所提出的运动规划模型在一般场景下具有极高的循迹精度。

实车测试速度轨迹如图10所示。在弯道及交叉口转弯场景中，由于驾驶安全的考虑，车辆速度无法达到期望速度，因此，仅统计车辆在正常直线巡航过程中相对期望速度的速度误差。此外，50km/h期望速度以下的测试在如图7场景①所示的园区内部道路上进行，而当期望速度为50km/h时，直线距离已无法满足加速到期望速度的需求，车辆尚未到达期望速度即需减速过弯，因此速度误差较大，达到2.65 km/h。而在其他期望速度下，速度误差随着期望速度增加而减小，这是因为随着速度的增加，车辆不再需要频繁切换档位，车辆底层对于加速度的执行精度提高，进而提高了速度追踪的精度。在所有期望速度下，最大速度误差为3.32km/h（期望速度10km/h），这证明本文所提出的运动规划模型在纵向具有较高的控制精度。

此外，在求解速度方面，图11记录了实车测试中81次运行的计算速度，其平均值为5.15毫秒，最大值为7.80毫秒，小于车辆底层控制执行频率20毫秒，这说明本文所提出的运动规划模型求解效率较高，能够满足实车应用需求。

图9 实车测试横向误差

表2 实车测试横向平均绝对误差

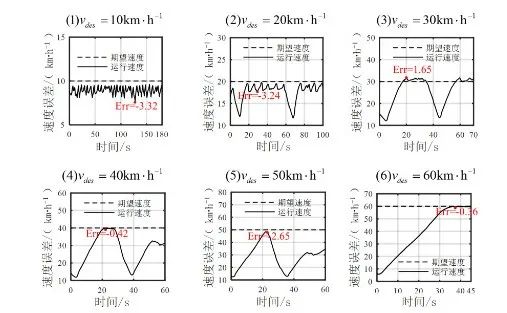
图10 实车测试速度轨迹

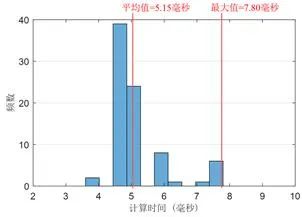
图11 实车测试计算速度

5

结  语

（1）本文基于优化控制方法，建立了适用于智能网联车辆决策控制的运动规划模型。相较传统模型，该模型基于时空混合域建模、考虑车辆动力学、考虑转向传动系统动态、考虑底层控制时延，从而提高了模型控制精度。

（2）该模型的控制效果经过仿真与实车测试验证，结果表明，在直线换道、曲线巡航、U-turn三种仿真场景中，循迹误差均在9 cm以下，速度误差在0.7 km/h以下；在60 km/h以下的直行、换道、交叉口转弯、曲线巡航实车测试场景中，最大循迹误差为12.5cm，直线巡航速度误差小于3.32 km/h。在期望速度20 km/h的直行及半径小于15 m的弯道场景下，本文所提出的模型循迹精度为11cm，较前人测试精度提高27%。

（3）本文提出的运动规划模型采用一种基于动态规划原理的求解算法，保障了模型求解效率。在实车测试中，模型平均求解速度达到5.15毫秒，满足实时性要求。

（4）未来研究可考虑赋予智能网联车辆运动规划以节能、安全、舒适等多目标，从而使智能网联车辆满足多种驾驶需求。

本文主要内容出自于《中国公路学报》2022年第3期 AI赋能网联车辆·大数据驱动智能交通专刊