数值计算中需要知道的小细节

我们在做完测试后，需要对测得的数据进一步处理，比如滤波，设置FFT分析时的重叠率与加窗等等。那么这些我们既熟悉又常用的操作中，有没有隐藏的小玄机呢？答案是肯定的。今天，我跟大家分享一下近期发掘到的这些小细节。

一、滤波

滤波就是为了保留或者去除信号中某些频率成分。比如，低通滤波，往往就是在软件中，设置一个频率值，然后就将高于这个数值的频率成分都移除掉。操作起来很简单，在Testlab软件中，具体参数设置如图1。

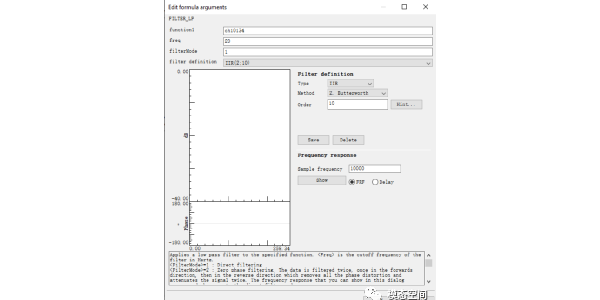
图1 低通滤波器参数设置

其中function1是需要被滤波的通道，freq是截止频率，filterMode是什么呢？可能大家都默认选择了1，这个呢就是一个小细节。我们先拿实际数据分析一下看看。这里需要处理的是一段CAN总线采集的转速数据，如图2所示。设置低通20Hz，我们要保留20Hz以下的频率通过，按照上图设置就完事了。但是结果真的是我们想要的吗？

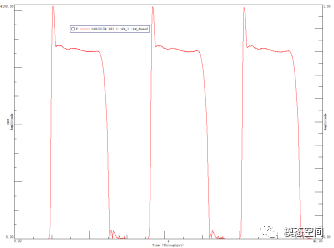
图2 原始转速曲线

我们看下按照图1设置得到的滤波后的数据，如图3所示。两条曲线看起来差不多，但是把峰值处放大了看一下。你就会发现问题所在了。如图4，红色曲线是原始信号，绿色的是滤波后的信号，整个信号竟然发生了相位偏移（时间延迟）。

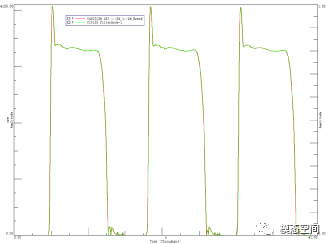
图3 滤波后对比图

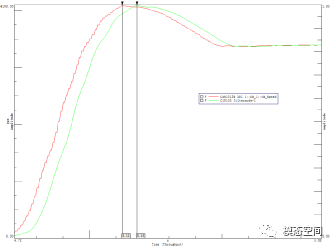
图4 局部放大图

是什么造成的呢？我们改变图一中的filterMode参数为2，再来计算一遍，看看结果如何。如图5。

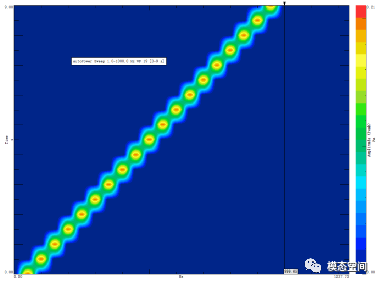
图5 零相位滤波与直接滤波的对比

紫色是filterMode为2的滤波后的数据，和红色曲线原始数据基本贴合，只是滤掉了高频成分。由此看出，filterMode这个参数很重要。它是什么呢？

在Filter的设置界面中，就有说明，filterMode=1是直接滤波，filterMode=2是零相位滤波。我们如果要保证数据滤波后不产生相位偏移问题，就需要使用零相位滤波。有很多文章说明了关于零相位滤波的具体计算公式，它的主要原理就是将时域信号滤波后，时间序列反转再次通过滤波函数，这样就保证了把偏移的相位又偏移回来了，去除了相位偏移问题。

那么平时滤波时是不是所有的信号都要用到零相位滤波呢？

也不是。如果单一分析某个测点的信号滤波后的幅值变化则不需要考虑零相位滤波。而如果有以下情况则需要考虑零相位滤波：

• 故障排除 - 在噪声和振动的多通道数据中，如果只对噪声通道使用滤波器，那么相对于振动通道，噪声数据会有一个时间延迟。当试图弄清楚一个振动事件是否产生了噪声时，这种时间上的错位会使我们很难看到振动和噪声事件是否有关联。

  
  

• 工作变形分析 - 如果在工作变形分析中使用的一些振动通道应用了滤波器，而其他的没有，这将导致这些通道之间的相位关系被改变。因此，工作变形动画将是不正确的。

二、重叠率

也可以说是步长和频率分辨率的匹配。那这个重叠率会有什么坑呢？我们使用时域计算器中的信号生成函数得到一个扫频数据，频率从1Hz扫频到1000Hz，时间为10s，幅值为1Pa。如图6。

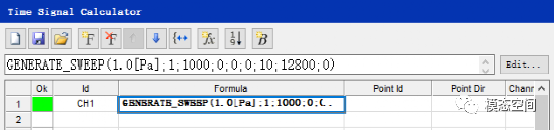
图6 生成扫频信号

对它进一步做跟踪时间的频谱计算，得到colormap图。参数设置为，频率分辨率为1Hz，步长为0.5s，因此重叠率为50%，得到的colormap如图7。好像一串冰糖葫芦。

图7 重叠率为50%的colormap图

如果我们把步长改为0.2s，其他参数不变，那么重叠率为80%。计算得到的colormap图如图8。

图8 重叠率为80%的colormap图

此时，曲线看起来就清晰得多，不会产生错误的理解。究其原因，主要是因为原始信号线性扫频，一秒钟频率从1变到100Hz，变化很快，而步长太大，重叠率太小的话，会使得两条谱线之间的频率差距太大，所以得到的colormap图就会有像糖葫芦一样的突变。由此，我们在实际旋转机械测量时，尤其是转速变化较快的机械，设置的步长以及频率分辨率参数一定要合适，不然就可能得到容易令人误解的结果。

三、窗函数

我们都知道在傅里叶变换时使用窗函数来避免泄露，有很多窗函数类型，如汉宁窗，矩形窗等等，常用的是汉宁窗。我们这里对50Hz单频正弦波做傅里叶变换，频率分辨率为1Hz。看看不同窗得到的结果，如图9。

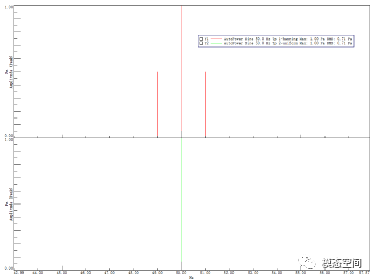
图9 单频信号汉宁窗和矩形窗对比

从图9中看到，原来的单频谱线，经过汉宁窗后竟然分成三条谱线（红色），而经过矩形窗后，反而得到的结果更好，只有一条谱线（绿色）。为何汉宁窗会有三条谱线呢？我这里查阅了很多论文，都说到汉宁窗的频谱是3个矩形窗频谱之和，如下面公式，其中 ω 是矩形窗频谱，括号中两项是相对于第一个频谱窗左右各移动了 π 。

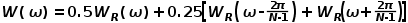
本例中， π ，也就是说将在50Hz处的频谱的基础上，还得到左右各1Hz偏移的频谱，并且左右两侧频谱是中心幅值的一半。

个人感觉理论公式有些绕，而我们同事（蒋校长）给了一个提示，我感觉能够更好的帮助理解。因为汉宁窗时域形状是升余弦窗，时域上与原始信号相乘后，再做周期延拓，得到的信号类似于调制信号，调制频率就是窗的时间周期的倒数，这里截断的时间为1s，所以调制频率就是1Hz，那做完傅里叶变换后的数据，就会在载波频率50Hz两边出现两个边频带，间隔频率就是1Hz。

说完理论后，我们再看看信号中有多个频率信息的数据，结果又会如何呢？我们计算一个包含50Hz和52Hz的时域信号，对它进行傅里叶变换，频率分辨率还是1Hz，然后查看不同窗的结果，如图10。

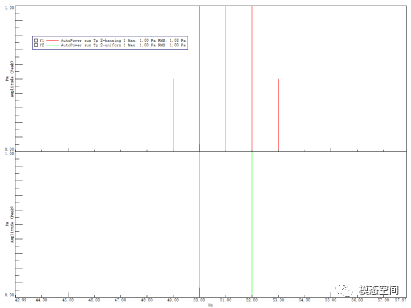
图10 多频信号汉宁窗和矩形窗对比

从图10看到，包含两个单频信号的时域数据经过汉宁窗后，在51Hz处产生一个不存在的谱线（红色）。而经过矩形窗，还是两条谱线（绿色），分别是50Hz和52Hz。

那么你肯定会想，为什么大多数软件以及论文都推荐使用汉宁窗呢？那是因为我们这个例子中，选取的频率分辨率为1Hz，也就是截取的时间段正好是整周期，并且数据是周期性的，所以矩形窗的结果最好。而如果频率分辨率为0.3，截取的时间段不是整周期，那结果如何呢，见图11。

图11 非整周期截取

由上图看到，矩形窗得到的结果（绿色）能量泄露的很厉害，而且最大值也明显低于汉宁窗得到的结果（红色）。而我们平时分析的测试数据，是不清楚里面的频率成分，所以如果使用矩形窗，那能量泄露的结果就会导致最大值的误判。以上也证明了，矩形窗适合周期性信号，频率分辨率很高，而汉宁窗适合非周期性信号。

那么使用汉宁窗时，如何避免出现图10那样的错误呢？我们再提高频率分辨率到0.2看看。

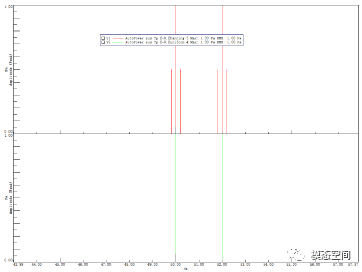
图12 提高频率分辨率

图12中，频率分辨率为0.2，经过汉宁窗后得到的谱线（红色）能够很清晰地分辨出两个频率值。因此，在常规的测试中，我们总说要提高频率分辨率，这样才能更精确的识别出故障频率。

总结，以上三个小案例是近期很多人遇到的问题总结。经常会有这样的提问，我在测试时，分析参数设置多少合适呢？答案是没有最好的，只有适合的。所以，你首先得了解被测件的结构特点，然后可以多选几组分析参数来进行对比，最终找到适合的。

作者简介

孙恬恬，博士，曾经在某主机厂工作多年，具有丰富整车性能管理经验。