车辆横向动力学前馈控制中的几种常用方法

近年来，无人驾驶技术越来越成熟，车辆行驶控制作为无人驾驶的关键技术之一，吸引了众多国内外专家学者的关注。行驶控制是智能车辆研究领域中的核心问题之一，指根据当前周围环境和车体位移、姿态、车速等信息按照一定的逻辑做出决策，并分别向油门、制动及转向等执行系统发出控制指令。智能汽车的行驶控制主要包括纵向控制和横向控制。纵向控制是指调整车速使车辆间保持足够的空间，使用最少的制动保持相对恒定的车速，并在紧急情况下尽可能快的制动；横向控制是指路径跟踪，即通过自动转向控制使车辆始终沿着期望路径行驶，同时保证车辆的行驶安全性和乘坐舒适性。

由于汽车是一个强耦合变参数的非线性系统，汽车的纵向运动和横向运动存在很强的耦合关系，耦合效应包含3类：运动学耦合、轮胎力耦合以及载荷转移耦合。对于运动学耦合效应，例如转向轮的侧偏力，实际在纵向有一个分量，从而影响纵向加速度，又如横向离心力是纵向速度和曲率的函数；轮胎的侧偏力与纵向力也是相互耦合的，对于给定的轮胎路面摩擦系数，作用在每个轮胎上的侧向力和纵向力相互限制，使合力不会超过附着极限；载荷转移也有显著的耦合效应，当载荷转移是由纵向加速度引起时，前后轮胎的垂直载荷重新分配将对横向动力学产生很大的影响。

考虑到这些复杂的非线性和不确定性因素，Rajamani在《Vehicle dynamics and control》一书中指出，必须采用前馈+反馈的控制结构才能保证车辆横向控制的效果，其中，前馈控制能够给方向盘提供一个可快速响应的控制输入，抑制系统静差；反馈控制利用跟踪误差反馈减小模型误差、道路曲率对控制精度的影响。因此，本文主要介绍了车辆横向动力学前馈控制的五种常用方法，并给出了其数学模型与推导过程。

1.自适应前馈控制

根据公众号文章：车辆二自由度动力学模型建模及其离散化应用和一种面向二自由度动力学模型应用的控制器和观测器设计迭代方法可得车辆横向二自由度动力学模型，并将其写成状态空间的形式为

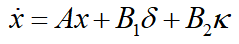
其中，系统矩阵为

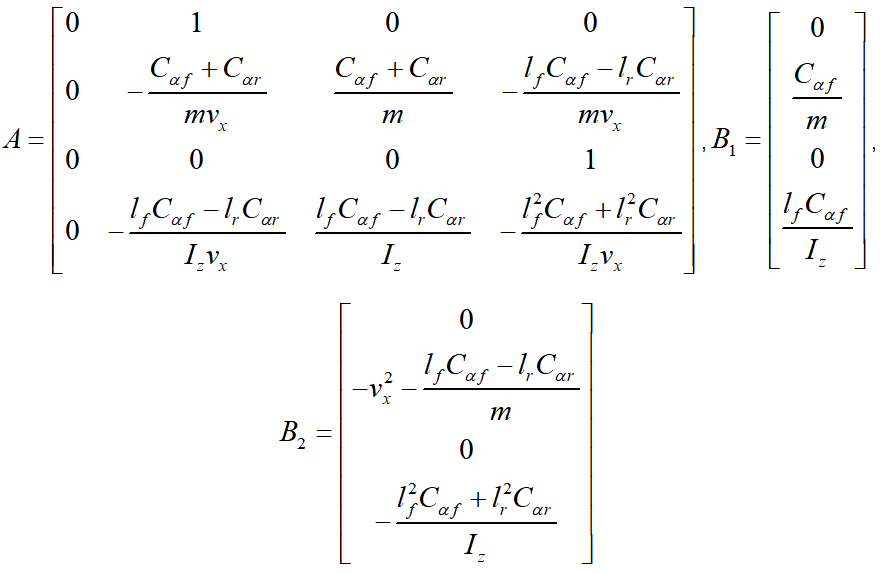
假设系统的控制输入由前馈和反馈组成：

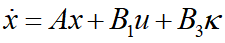
代入可得

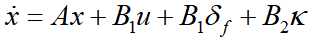
其中

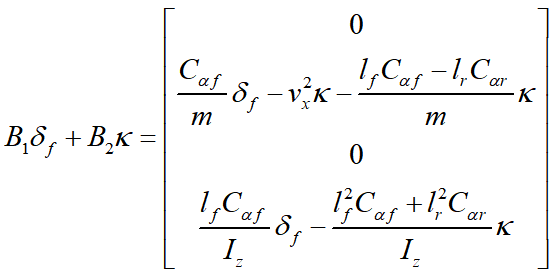
假设前馈控制器能让de1的前馈偏差为0，可得：

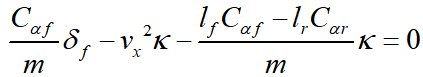
则控制器的前馈为

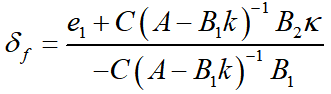
此时，代入前馈后的系统为

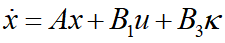
其中，

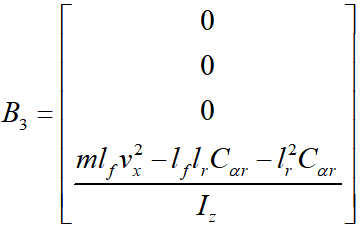
由此可见，引入前馈后，系统的干扰增益矩阵发生变化，系统的抗干扰性能得到改善。在此模型基础上，所设计的反馈控制系统性能将更优。

2.基于拉氏变换和终值定理的前馈控制

在状态反馈u=-Kx的作用下，用于闭环侧向控制系统的状态空间模型可表示为

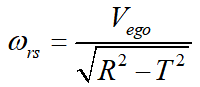
由于

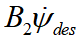
项的存在，当车辆在弯道行驶时，即使矩阵趋于稳定，跟踪误差也不会完全收敛到0。

很自然的想到，假设转向盘控制器可由状态反馈加上前馈得到，以试图补偿道路曲率

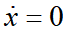
闭环系统可以表示为

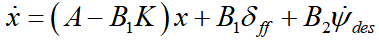
采用Laplace变换，假设为0初始状态，可得到

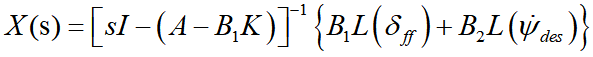
如果车辆在路面上以恒定速度vx和恒定转弯半径R行驶，那么

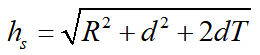
它的Laplace变换为

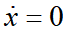
。同样，如果前馈是常值，那么它的Laplace变换为

。

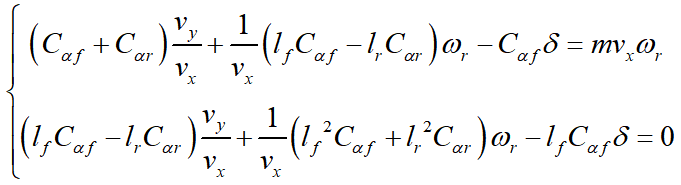
利用终值定理，稳态跟踪误差可表示为

则稳态误差为

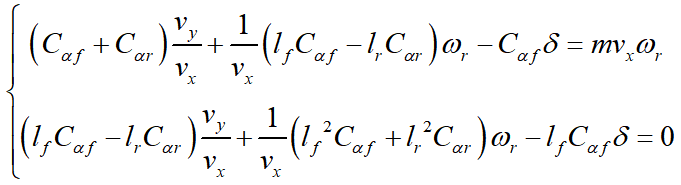
通过上式可以看出侧向位置误差e1可以通过合理选择前馈值

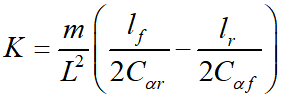
而被置为0。然而上式所示，

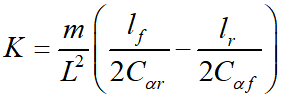
不影响稳态偏航误差。不论前馈转角如何选择，方向角误差总存在不可修正的稳态项。稳态方向盘误差为

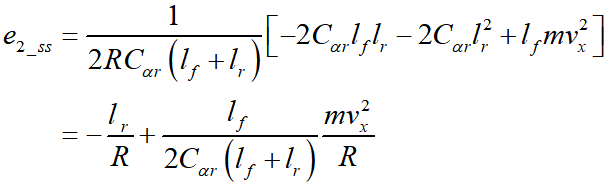
如果选择前馈转角为以下值，稳态侧向位置误差可以为0：

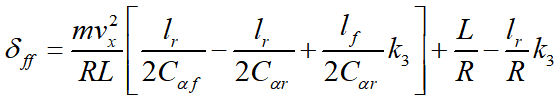
可近似看作

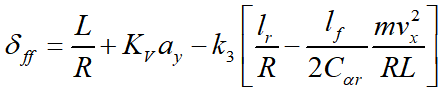
其中

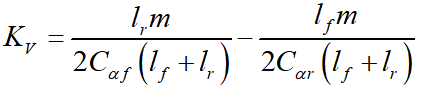
以及

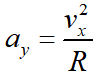
3.基于二自由度模型横摆稳态响应特性的前馈控制

二自由度汽车运动微分方程式为

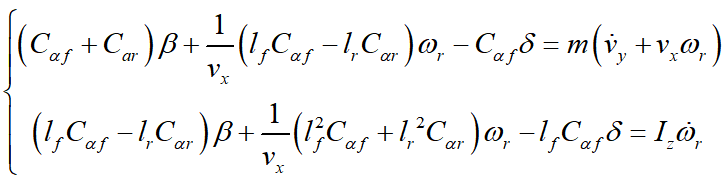
汽车稳态时横摆角速度wr为定值，此时

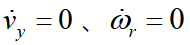
以此代入上式得：

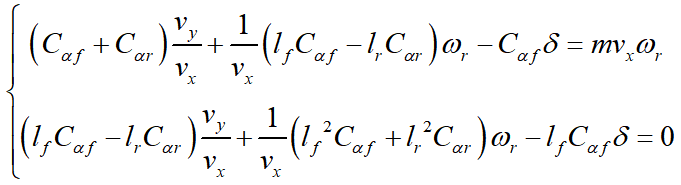
将两个式子联立并消去vy，可得横摆稳态角速度增益为

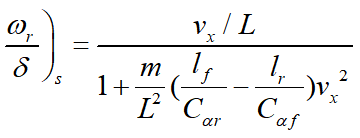
通过

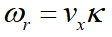
可以得到

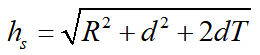
4.基于驾驶员预瞄模型的前馈控制

车辆二自由度模型

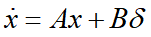
其中，

如下图所示，假设车辆沿着一个期望的半径为R的圆周轨迹稳态行驶，预瞄距离为d，e为预瞄横向偏差，h为预瞄点到转向中心的距离。根据车辆二自由度模型，可以得到车辆的稳态行驶状态满足下列方程

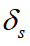
图1 车辆稳态圆周运动时的预瞄跟随示意图

可以得到车辆的稳态行驶状态满足下列方程

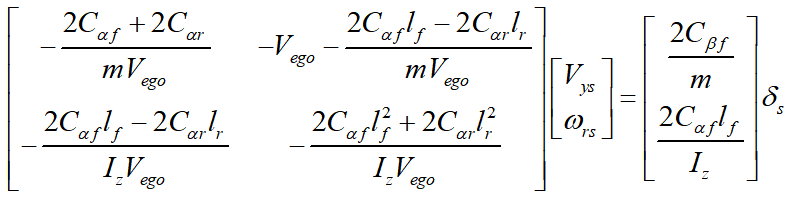
其中，

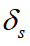
为稳态行驶时的前轮转角，下标s代表车辆稳态行驶时的状态量。根据车辆稳态响应

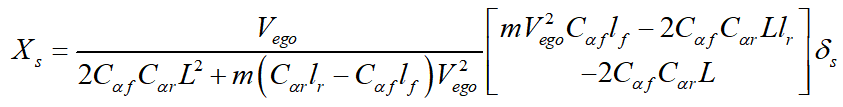
可得

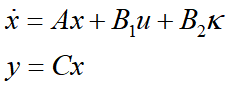
可见，车辆稳态行驶的侧向速度可以表示成横摆角速度与纵向车速的函数。根据车辆稳态圆周运动可得

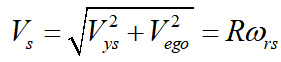
根据以上两式可得

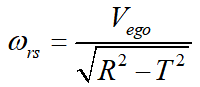
可得前轮转角输入与稳态横摆角速度的关系

其中，

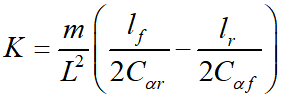
为稳定性因数或不足转向系数。则稳态行驶的前轮转角为

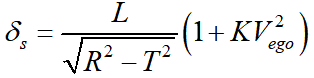
预瞄点到稳态回转中心的距离为

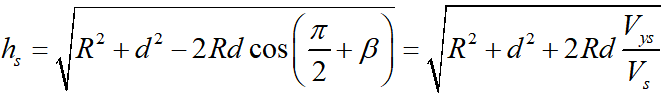
可得

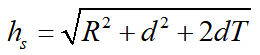
则横向预瞄偏差为

因此，期望的前轮转角与横向预瞄偏差之间的映射关系为

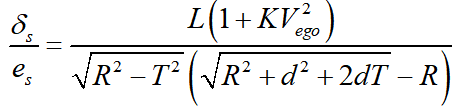
利用上述映射关系根据横向预瞄偏差可直接求得最优的前轮转角，因此，该关系式也被称为基于单点预瞄理论的最优转角前馈控制。由于该关系式较为复杂，一般用其简化形式。首先，已知条件

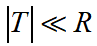
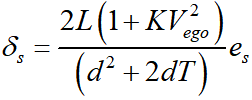
则根据泰勒公式可得

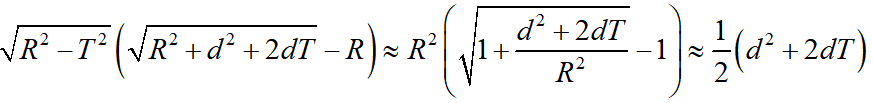
则上述映射关系式可简化为

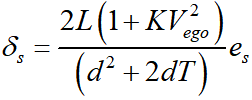
由上式可得，前馈与横向预瞄偏差成一定比例，但是该比例因子是一个非常复杂的动态变化的系数。

5.基于闭环系统平衡点的前馈控制

横向控制系统的状态空间模型为

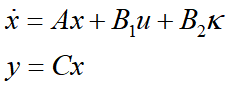
在状态反馈与前馈作用，下系统的输入为

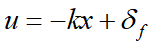
用于闭环横向控制系统的状态空间模型为

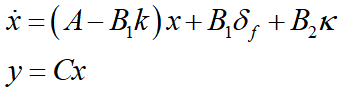
求状态空间的平衡点令

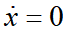
，得

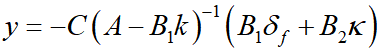
由于状态输出横向误差e1可测，得

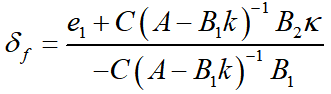
6.仿真分析

以上描述的前馈控制方法受道路曲率和横向误差的总结如下所示：

表1. 前馈控制影响因素关系表

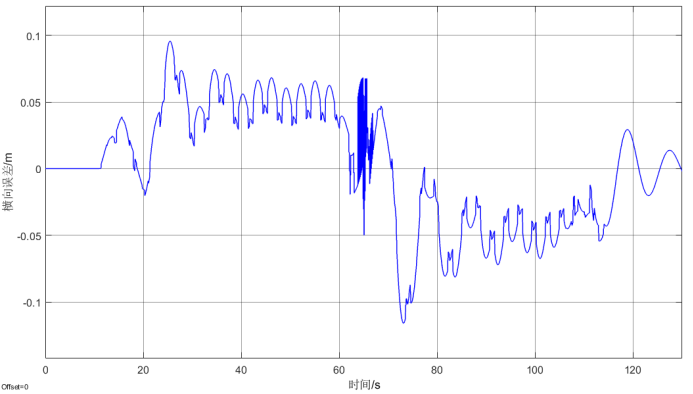
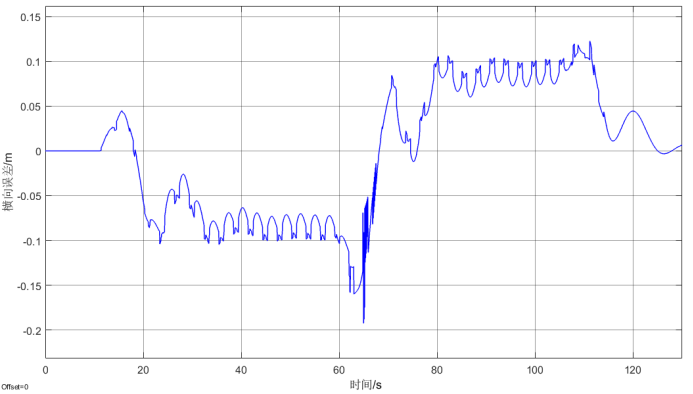
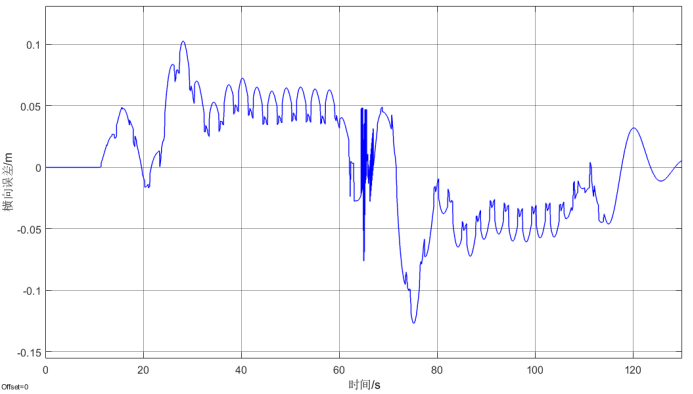
仿真基于LQR控制器反馈控制，此处对所介绍的五种前馈控制方法进行分析验证，在不同前馈控制方法下，车辆距离车道中心线的横向误差如下图所示。通过仿真结果可以看到，带有前馈控制的车道保持横向误差有明显的减小，不同的前馈方法有不同的优势，在左转弯的弯道下，驾驶员模型前馈控制方法的横向误差最小，在左右弯道变换时，基于闭环系统的平衡点前馈控制方法效果较好，横向误差波动小。

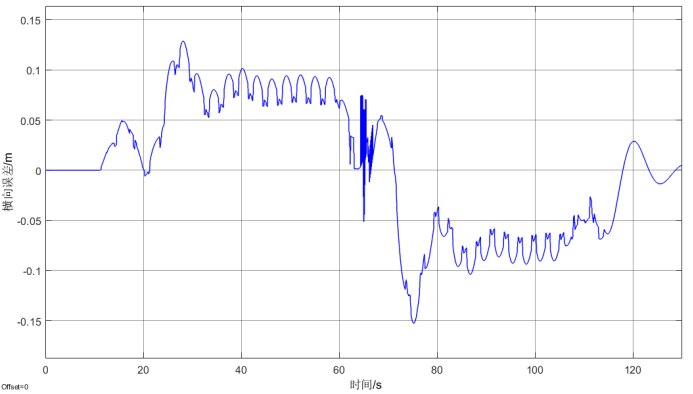
图2 无前馈时的横向误差

图3 自适应前馈控制的横向误差

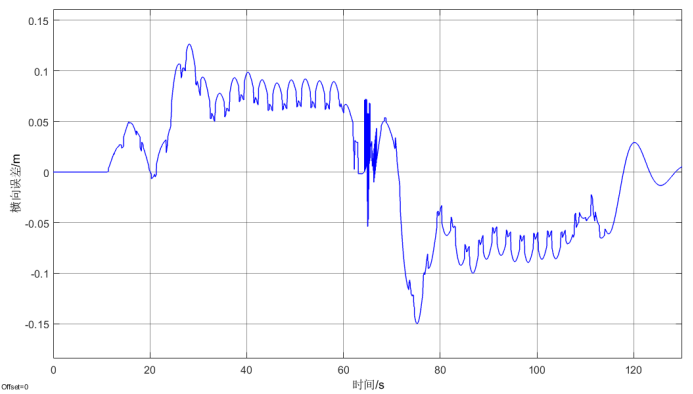
图4 基于拉普拉斯变换前馈控制的横向误差

图5 基于二自由度模型前馈控制的横向误差

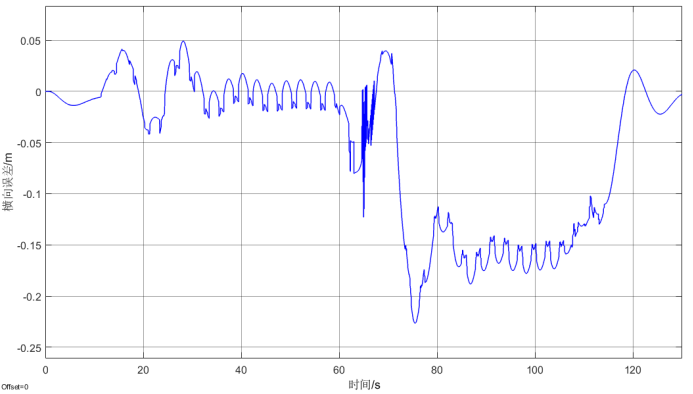
图6 应用驾驶员模型前馈控制时的横向误差

图7 基于闭环系统平衡点的前馈控制的横向误差