带有晃动水箱的移动车辆的晃动力特性

摘要

装有部分装满液体储罐的货车在瞬态运动期间会受到液体晃动的影响。车辆运动引起的晃动会对车辆产生额外的作用力，有时会对安全造成潜在威胁。以往对这一问题的研究通常使用质量弹簧类比来表示液舱的晃动效应。其主要缺点是必须事先进行CFD分析或实验研究，以便通过曲线拟合建立等效质量弹簧模型。本文采用频域边界元法和晃荡问题的解析解，推导了晃荡流体的模态方程和水动力参数。将通过与文献中可用的CFD结果进行比较，检查结果的准确性。然后，本文评估了等效质量弹簧模型的精度，并探讨了利用等效矩形储罐内晃动的解析解来近似圆柱形储罐内晃动效应的可能性。

1 简介

由货车瞬态运动引起的部分填充液罐内的晃动将对车辆施加额外的力和力矩。如果外部激励满足液体的固有频率，可能会产生较大的力和力矩，这有可能使车辆倾覆。已经对识别晃动的固有频率以及由此产生的力进行了大量研究。McIver以积分方程的形式给出了卧式圆筒形储罐的解析解。Faltinsen给出了浅水假设下的简化解，并比较了圆柱形和矩形水箱之间的差异。采用边界元法或CFD进行了数值模拟。

然而，当试图将流体动力学研究的结果应用于车辆运动仿真时，存在一定的困难。对于任意填充高度的卧式圆筒形储罐，很难找到其固有频率和晃动力的简单解析解。数值方法适用，但通常很耗时。

因此，许多研究人员将晃动的液体简化为与车身相连的线性质量弹簧模型[3-4]或摆锤模型[5]。这种方法的缺点是需要数值模拟结果来校准模型。

本文的目的是提出一种利用有效的频域边界元法和晃动问题的解析解来考虑运动车辆晃动效应的方法。将结果与之前文献中的CFD结果进行比较，以证明该方法的准确性。

2  流体力学公式

在线性势理论中，不可压缩、无旋转流体的运动由以下主导方程控制：

                                   （1）

其中，是速度势，是描述流体域中速度场的标量函数：

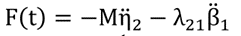
              （2）

方程的解取决于流体域的边界条件。对于储罐中的液体，固体壁边界条件（3）适用于储罐表面。在平均水位上，采用线性化运动学（4）和动力学自由面边界条件（5）：

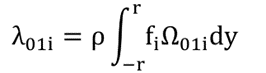
                                （3）

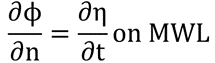
                              （4）

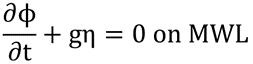
            （5）

此外，流体应始终遵守质量守恒定律，由此可知，沿平均水位的自由面高程积分应为零：

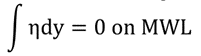
                               （6）

其中η是自由面高程。在不进行详细说明的情况下，横向激励下车身的运动可以通过以下模态方程来描述：

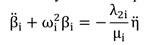
                           （7）

其中β是用于描述液体运动的广义坐标；η是横向的外部激励；μ和λ是以下形式的水动力参数：

                            （8）

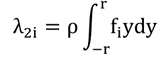
                               （9）

i=1,2,…,m为晃动模式。第一晃动模式产生的合力和力矩表示为：

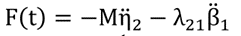
                    (10)

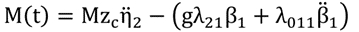
                (11)

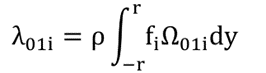
                         (12)

λ011是横摇-横摇耦合项。特别是，如果油箱的规定运动是谐波运动：

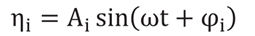
                          (13)

那么模态方程βi（12）的稳态解也是调和的，晃动力可以表示为：

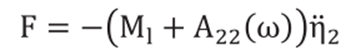
                      (14)

其中

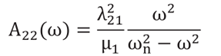
                              (15)

类似地，横摇-横摇耦合项也可以写成A24。因此，方程式（14）中的晃动项将具有与第一个惯性项相同的形式。结果表明，在简谐激励下，液体晃动的效果与向储罐中添加额外质量的效果相同。该质量的值取决于激励频率，可以是正的，也可以是负的。在这种情况下，将不再需要（7）形式的独立模态方程，可以通过在油箱的原始质量上添加与频率相关的质量项来描述晃动效应。方程（11）中的晃动力矩也采用了类似但稍微复杂的附加质量推导。此项目Aij称为附加质量，将在下一章的研究中使用。

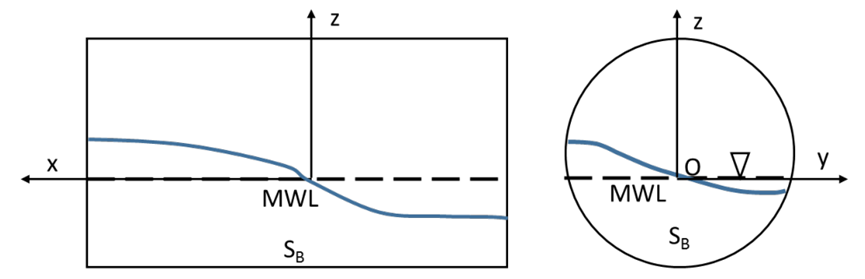
方程式（10）和（11）显示了晃荡力和力矩的分量。对于晃动力，第一项是液体质量的惯性，而第二项取决于水动力参数λ21，后者仅取决于自由表面形状。对于晃动力矩，它有一个类似的惯性项，然后第二项由晃动决定，最后一项由平动自由度和转动自由度之间的耦合共同决定。下图1。显示了油箱固定坐标系和用于描述油箱6自由度刚体运动的惯例。在方程式（10）和（11）中，下标η2是沿y轴的横向运动。

图1用于晃动问题的约束

3 稳态晃动的频域数值模拟

对于任意形状的水箱，很难得到自由表面高程和晃动速度势的解析解。在大多数情况下，必须采用数值方法。这意味着速度势必须在每个时间步求解。为了避免耗时的时域模拟，海洋工程中广泛使用的一种方法是将激振力和储罐运动视为一系列稳态谐波分量的叠加。对于每个频率，都会有一个与频率相关的附加质量形式的解，如等式（14）所示。

在计算频域响应函数后，通过傅里叶逆变换得到了时域晃动运动和晃动力。采用边界元法（BEM）程序求解晃荡的频域响应。该程序利用格林第二公式解决了边值问题。通过定义拉普拉斯方程的基本解，将求解流体域中速度势的问题转化为计算沿体表的边界积分[6]。边界元法在计算效率方面具有显著优势，因为它只需要对油箱表面进行网格划分。在求解速度势后，通过对体表压力积分得到与频率相关的附加质量。

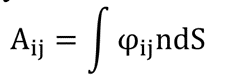
            （16）

4 瞬态晃动计算和基准研究

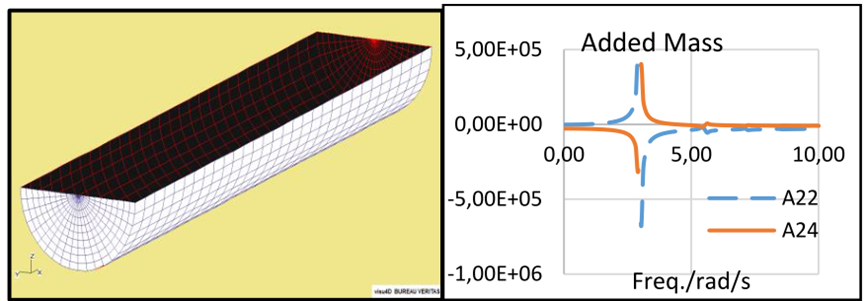
为了证明流体动力学方法的有效性，并提供解决问题的基本程序，对装有部分加满汽油箱的转向车辆进行了基准研究。车辆从零速度开始转向，并在其瞬态期间引起晃动。全曲线加速度为0.6 m/s2。储罐按2D尺寸考虑，长度15.5m，半径1.5m，填充水平50%。在本节中，我们使用直接流体动力学参数来获得晃动力和力矩，并将我们的结果与弹簧-质量模型的精度进行比较。油箱型号如下所示。x沿水箱纵轴，y沿水平轴，z位于平均水面。

图2边界元模型和计算附加质量

结果如下所示。方程（17）和（18）中附加质量的解析解表明，附加质量取决于激励频率。当激励频率等于固有频率时，它将变为无穷大，在无限激励频率时，它将趋于有限值。在数值模拟中，不可能得到无穷大的值。附加质量在固有频率附近达到非常大的值，导致图中出现双峰。该双峰的渐近线所在的频率为固有频率。可以看出，在这种情况下，固有频率为2.97 rad \/s。质量基于液体的3D总质量。对于二维分析，将使用截面质量。此外，可以看出，第一晃动模式是最常见的模式。第二个晃动模式（接近5.5 rad \/s）几乎消失。车辆的规定运动如下所示。过渡期持续3.07 s，然后车辆以全曲线行驶9.25 s。从t=9.25s开始，车辆线性减速3.07 s，然后沿着直线行驶。加速度可以描述为：

        （17）

在这种情况下，我们可以看到规定的运动是一个具有有限时间长度的非光滑函数，这意味着该运动不能被视为稳态谐波激励。因此，边界元法计算的附加质量不直接适用。

在已知运动的情况下，下一个要求是获得晃荡力的水动力参数。但如上所示，边界元法软件倾向于解决耦合晃动问题，在该问题中，总晃动势已得到解决，而无需对其进行分解。第1节中表示的规定运动下的晃动力与附加质量没有直接关系。我们仍然需要从附加质量结果中获得所需的参数。要计算的水动力参数为λ21和λ011。

附加质量可用于推导这些参数之间的关系。让激励频率为无穷大，我们得到：

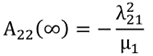
                  （18）

A24可以用类似的方式表示。水动力参数与无限频率下的附加质量有关。然而，当附加质量的计算仅提供两个方程时，就存在三个未知数。精确的特征函数f2,1（也是晃动期间自由表面的模态形状）没有完整的解析解。由于还需要一个方程，我们选择使用自由面高程f2,1的试验函数来获得近似解。

我们用于自由面高程的试验函数是余弦函数，它是矩形水箱的特征函数：

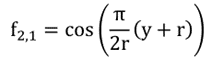
             （19）

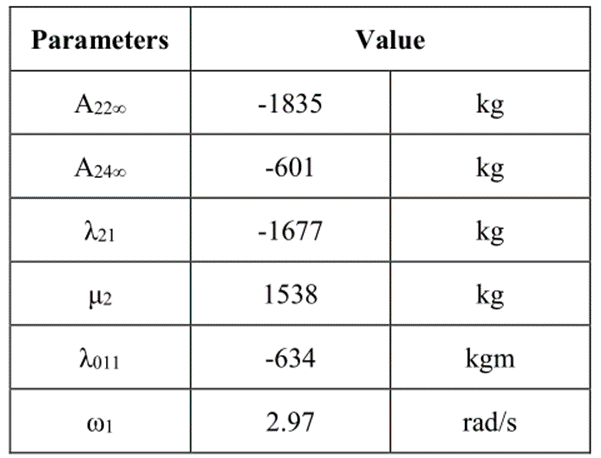
它是一个奇函数，满足质量守恒边界条件（6）。不一定满足运动学和动力学自由面边界条件。结合给定的附加质量，我们得到了对三个未知量μ2、λ21和λ011的估计。可以计算模态方程和晃荡力。计算的参数以及晃动力和力矩如下所示。

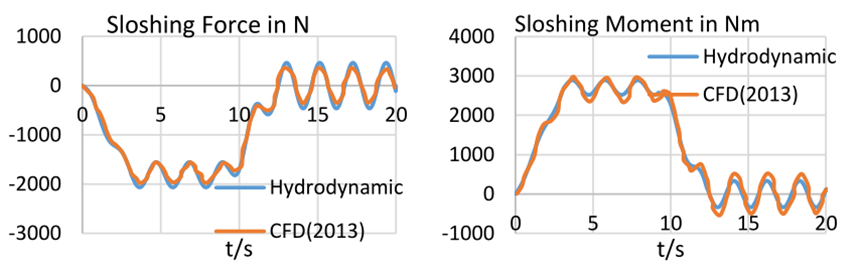
图3流体力学和CFD结果的比较

表1 计算和导出的参数

5 结论

本文旨在提供晃动动力学和车辆动力学之间的接口，并通过基准研究证实了所提出方法的可行性。应用线性势流理论，用模态方程和流体力学参数描述液体晃动。为了填补稳态晃动计算结果与瞬态晃动计算所需输入之间的差距，使用了自由面高程的试验函数。导出的模态方程和水动力参数可与货车运动方程一起求解，得到晃荡力和力矩。

这种方法的优点是，它用更高效的边界元分析代替了校准所需的耗时的CFD分析，并且可以通过向边值问题添加一个额外维度轻松地扩展到3D。此外，它还能够解释晃荡机制，包括自由度之间的耦合效应、存在外力矩时由Stoke-Joukowski势引起的附加力矩以及更高的固有模态。然而，它也继承了线性势流理论的挫折：液体的粘度效应只能简化为线性阻尼比，而非线性效应不包括在内。未来，该方法将扩展到6自由度运动，并应用于实际车辆操作，如制动、转弯和在不平的地面上行驶。

文章来源：Mengmeng Han,Jian Dai,Kok Keng Ang,“Hydrodynamicaspects of moving vehicle with sloshing tanks”，MATECWeb of Conferences 211, 15002 (2018).https://doi.org/10.1051/matecconf/201821115002

AutoAero是吉林大学张英朝教授团队建立的专业汽车空气动力学微信公众号号，致力于普及汽车空气动力学知识，传播汽车空气动力学。推广包括流体力学基本理论，汽车空气动力学及热管理水管理等基础知识，乘用车气动造型设计，卡车气动造型设计，风洞实验技术等多方面的内容。欢迎有兴趣的专业人士阅读、关注、共享！