广告
自动驾驶控制算法 — 车辆动力学模型
在自动驾驶车辆控制中，车辆模型的建立和分析是进行控制器设计的基础，在之前我们详细介绍了车辆在全局坐标系和道路坐标系下的运动学模型，如下链接：
自动驾驶控制算法 — 车辆运动学模型
但在实际的车辆控制过程中，某些场景下车辆的动力学特性不能忽略，比如高速场景、转弯场景等，都需要对车辆的动力学模型进行有效地建立。为此，本文将分别介绍车辆在全局坐标系和道路坐标系下的动力学模型，为后面的控制器分析设计提供依据。
1. 全局坐标系下的车辆动力学模型
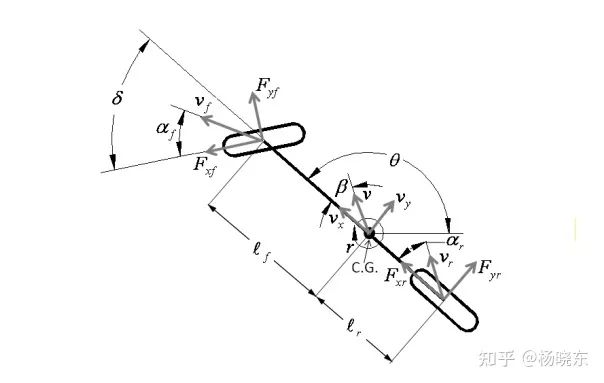
图1 车辆动力学模型
在进行车辆动力学建模时，车辆上的横向力将是重点关注的问题。在这里假设纵向车辆速度是单独控制的，在给定车辆质量
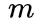
的情况下，将图1所示的车辆侧向力相加，得出：
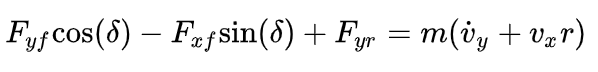
其中，
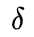
为前轮转角，
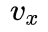
和
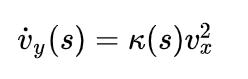
为车辆质心处的纵向速度和横向速度，
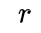
为车辆的横摆角速度，
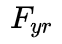
和
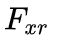
为车辆后轮上的横向力和纵向力，
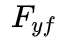
和
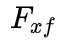
为车辆前轮上的横向力和纵向力。
假设车辆只在平面内运动，则车辆的力矩平衡方程为：
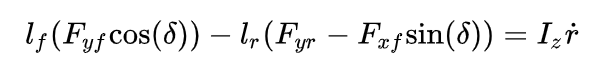
其中，
和
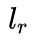
为车辆质心到前轮和后轮中心的距离，
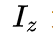
为车辆绕
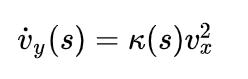
轴的转动惯量。假设车辆没有横向滑移，前后轮胎的侧偏角
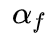
和
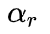
可以表示为：
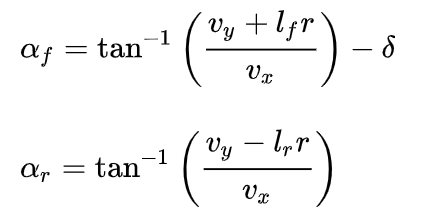
轮胎侧偏角的含义是车辆轮胎的朝向和轮胎速度方向的夹角，因为车辆转弯需要有向心力，轮胎的侧偏角可以帮助车辆提供一定的横向力。
假设车辆轮胎为线性模型，即轮胎横向力和侧偏角成正比，即：
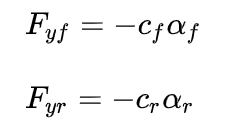
其中，
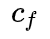
和
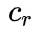
分别为前轮和后轮的侧偏刚度。
假设车辆纵向速度为常值，即
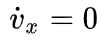
，并假设
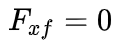
，整理前面的公式可以得到车辆在全局坐标系下的动力学模型为：
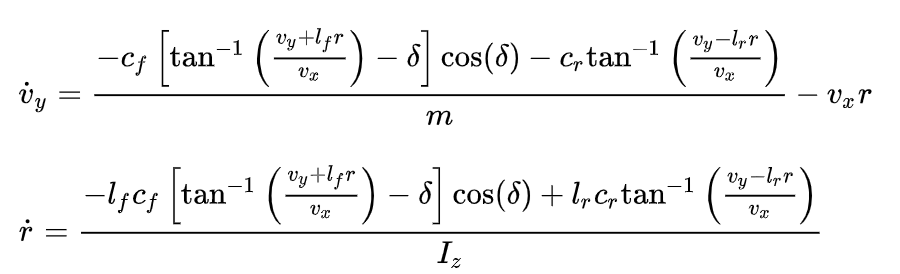
上述模型很明显为非线性模型，为了简化，我们对其进行线性化处理，利用三角函数的小角度近似之后，可以得到：
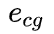
进一步整理，可以得到完整的车辆线性动力学在全局坐标系下的表示：
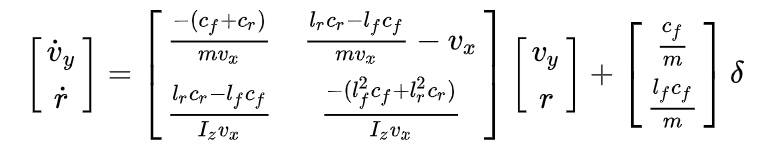
2. 道路坐标系下的车辆动力学模型
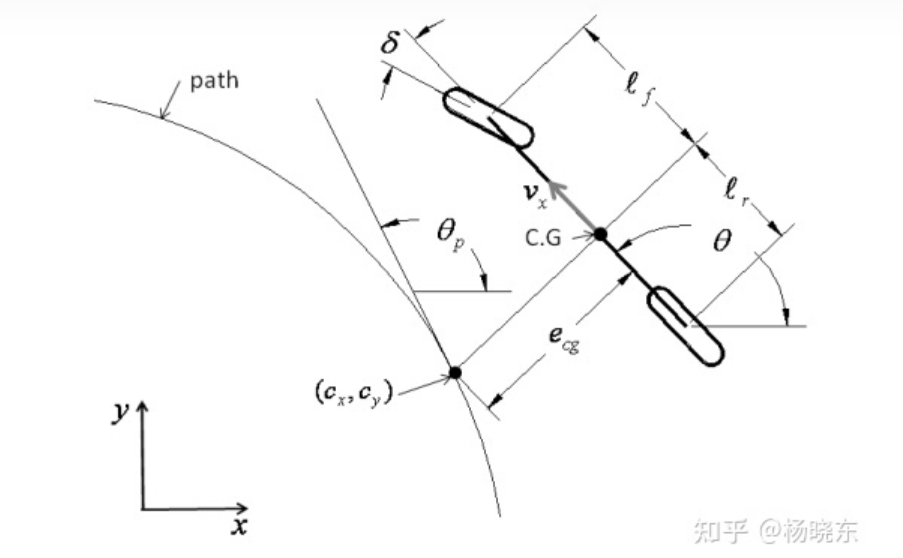
图2 道路坐标系下的车辆动力学模型
在道路坐标系下进行动力学模型的建立，将会有助于我们进行模型分析和控制器设计，如图2所示为车辆在道路坐标系下的动力学模型。同样假定纵向车速恒定，则车辆横摆角速度可表示为：
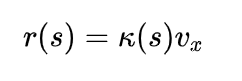
其中，
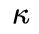
为道路曲率。车辆横向加速度有：
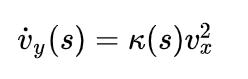
假设
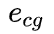
为车辆质心到道路参考线的横向误差距离，则有：
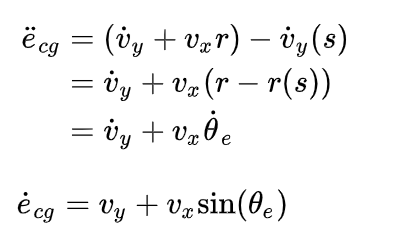
其中，
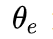
为车辆和参考线之间的航向角误差。
我们将上式进行替换整理，可以得到车辆动力学模型在道路坐标系下的表示：
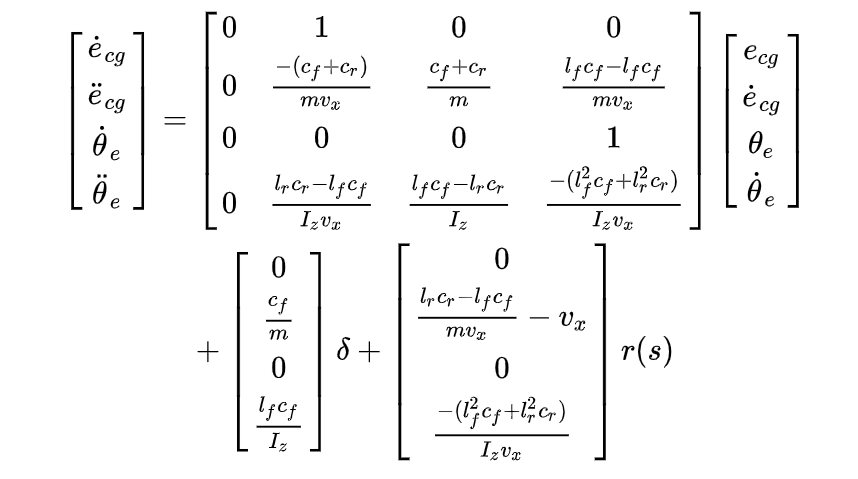
其中，
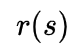
表示的是参考轨迹线的期望横摆角速度，即
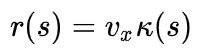
。至此，我们得到了车辆动力学模型在全局坐标系和道路坐标系下的方程表示，在后续的自动驾驶车辆控制器设计分析中可以根据需要进行选择使用。
- 下一篇：燃料电池的效率、功率与温度有什么关系
- 上一篇：轴向磁通电机技术综述
广告 
广告
编辑推荐
最新资讯
-
测迅乌镇&盐城测试场：助力智能网联汽车标
2025-02-22 12:39
-
使用示波器对三相电机驱动器进行测量
2025-02-22 12:37
-
上汽集团大乘用车重磅招聘
2025-02-22 12:25
-
GB/T 44173-2024对开门预警DOW的要求
2025-02-22 12:25
-
声音工程：像用PS一样编辑声音
2025-02-21 17:04
广告
广告
