基于欧姆内阻压降的电池簇不一致性在线监测方法研究

文章来源：1.国网湖南省电力有限公司经济技术研究院2.规模化电池储能应用技术湖南省工程研究中心3.长沙理工大学电气与信息工程学院

0引言
储能是推动新型电力系统发展与实现“双碳”目标的主要手段与核心技术，其中锂离子电池储能在国内储能项目中占有重要地位。随着“新能源+储能”发展模式的大范围推广，储能电池安全问题的日益受到各界关注。
基于现今已有成果，关于单体电池健康状态的预测方法主要包含健康因子的提取、建立电池模型以进行参数辨识及多模式组合的方法。同时，部分学者与机构在面对庞杂的锂离子电池特性数据时，通过找到能够表征电池退化的特征来建立此种特征与电池健康之间的关系。如韦海燕等构建电池欧姆内阻增加量、极化内阻增加量和极化电容减少量作为电池的健康因子以实现对电池健康状态的估算。
但不同于对单体电池的安全检测，储能电站往往以簇为主体，以簇成堆，其基本单元为电池pack箱，即由单体电池串并联组成。由于生产、筛选成组及外部工作环境存在一定差异，造成电池pack箱参数的差别。若对一致性问题不加以监测与管理，不仅会降低电池簇的使用效率更会增大pack箱体内电池老化速率，对储能电站运行寿命易造成不可逆的损害。相较于对电池簇老化程度的预测研究，现今研究重点已然集中在储能设备一致性问题上来。
对于电池簇不一致性的监测，往往着眼于容量的变化。多数文献指出电池簇可用容量大小遵循“木桶原理”，由最小容量的电池pack箱所决定的。在确定环境温度与放电倍率的情况下，若电池簇容量衰减速率符合基本要求，则判断其一致性较好。但是该认定方法是有前提条件的，即某一pack箱的剩余电量与可充电电量都为最小时，电池簇容量可等于该电池pack箱容量。但在实际工作中，存在某一pack箱的剩余电量为最小，其可充电电量并不是最小的情况，进而导致电池簇实际容量往往偏低，存在小于任意pack箱容量的情况，因此不能够简单的依据容量变化来反映电池簇的一致性情况。若通过对电池pack箱的欧姆电阻与极化阻抗进行实时监测以确定电池簇的不一致性，不仅需要在线参数辨识，而且需要大量的数据采集和计算。在储能电池管理系统中，大量的矩阵运算是难以在线实现的；而电化学阻抗谱（ElectrochemicalImpedanceSpectroscopy，EIS）也已被广泛用于分析和预测电池健康状况，但该方法检测对象通常是单体电池，电池pack箱则由多个单体电池串、并联组成，结构多样，如果对箱体内每个单体电池进行测试，则实际可操作性较差；如果直接测试pack箱，则必须进一步验证该方法的可行性。
同时，许多实际工程中使用经验和拟合方法预测电池状态，通过现有退化数据来预测未来电池的性能，无需详细了解电池的内部设计和材料特性。因此，为降低数据采集量及减少不良数据，本文以恒流放电为基础，通过探究在恒流放电过程中因不一致性而引发的电池簇与电池pack箱欧姆内阻压降浮动规律，提出一种基于欧姆内阻压降的电池簇不一致性在线评估方法，即以欧姆内阻的增量作为因子，将其以电池电压幅值的变化间接表现出来，通过实时监测数据的不断积累以实现对电池簇一致性的监测，在丰富簇级管理手段的同时，有效利用BMS所测得的实时数据。

1电池簇外特性分析
在脉冲放电方式下，单体电池端电压变化曲线如图1所示。

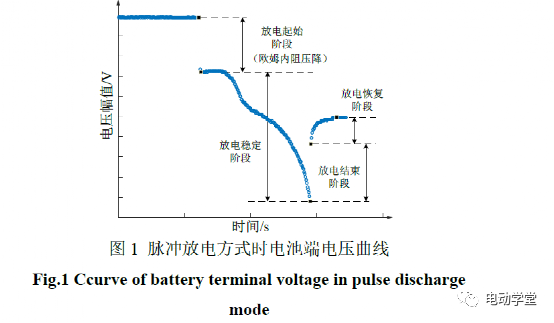
在放电起始阶段，电池电压存在一个瞬间下降，如图1所示。该压降主要是由于电池欧姆内阻分压所造成的，根据文献可知其数学关系如式（1）所示。

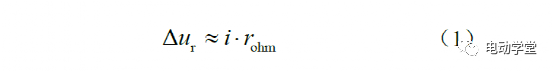
式中：i为放电电流；rohm为电池欧姆内阻。此时电池极化电容电压无法突变，初始电压为零，可视为短路。在放电电流与采样时间保持恒定的情况下，其压降幅值的大小可以间接反映出欧姆内阻大小情况。储能电站多以电池模组单元箱（电池pack箱）为基本单位来构建电池簇。对单个电池pack箱建立Thevenin电路模型，则电池簇可视为该电路模型的串联，其模型如下图所示。

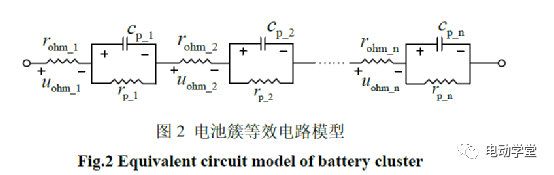
则在放电起始阶段，电池簇端电压与各电池pack箱端电压具有以下关系：

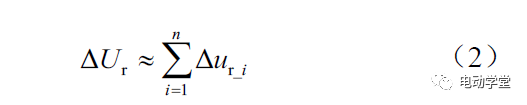
式中：ΔUr表示电池簇欧姆内阻压降幅值；Δur_i表示第i个电池pack箱欧姆内阻压降幅值。在运行初期，电池参数较为一致，因此对上式（2）进行进一步简化，如下式所示：

式中，n为电池pack箱个数，Δur表示某一电池pack箱的压降幅度，该电池pack箱可视为表征单体，以该单体为参考对象，为电池簇工作过程中的不一致性提供了参考。基于式（3），对电池簇与表征单体运行参数进行实时检测，并进行线性拟合得到函数关系f(nΔur)ΔUr，通过对线性关系变化速率k来反映出电池簇的不一致性情况。
2基于欧姆内阻压降的储能电站电池簇不一致性在线评估方法
2.1表征单体的选择在电池簇成组投运之前，基于可用容量与欧姆内阻两项参数指标，对电池pack箱进行筛选，筛选条件为：

即该表征单体的可用容量qchar和欧姆内阻rchar最为接近电池簇中所有电池pack箱可用容量的平均值和欧姆内阻的平均值，以该表征单体为参考对象，为电池簇工作过程中的不一致性提供参考。
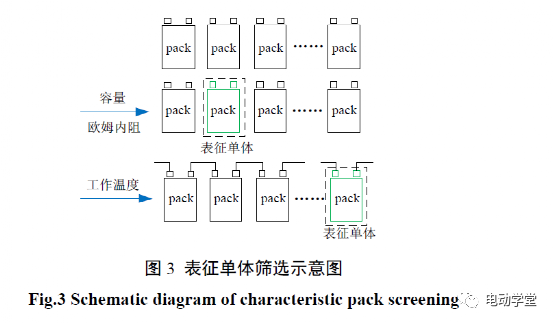
由于电池老化与环境温度有强相关性，在经过初期运行之后，以工作温度T为参数指标再次对电池pack箱进行筛选；同时表征单体以一个月或一个季度为周期进行动态筛选，筛选条件如下：

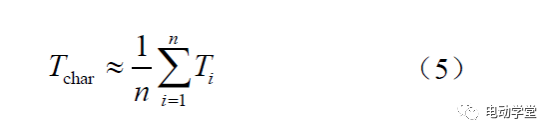
具体筛选过程如图3所示。

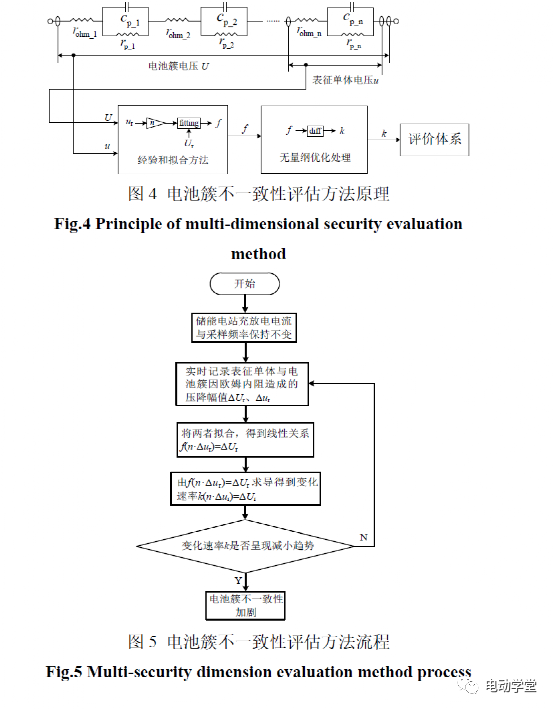
2.2电池簇不一致性在线评估方法分析令电池簇初始荷电状态、放电电流与系统采样频率保持恒定，获取电池簇与表征单体因欧姆内阻造成的压降ΔUr与Δur，并通过线性拟合得到函数关系f(nΔur)ΔUr，n为电池pack箱个数，基于线性拟合关系求导得变化速率k，进行无量纲化处理。
对变化速率k(nΔur，ΔUr)进行在线记录，若电池簇内某一电池pack箱受外界环境影响而老化程度加剧，欧姆内阻数值增大，导致压降幅值ΔUr逐渐大于表征单体nΔur，变化速率k将呈现增大趋势，即通过对线性关系f(nΔur)ΔUr变化速率的实时监测来反映出电池簇不一致性来构建安全评估系统。所述方法原理与流程分别如图4、图5所示。

3实验验证
实验平台主要由手套箱、生化培养箱、高性能电池监测系统与人机交互界面构成，如图6所示，培养箱温度维持在30℃。

3.1电压幅值分析实验对象为LiNiMnCoO2扣式电池，采用多枚锂离子扣式电池串联进行循环实验，实验采用的扣式电池为同一批制出，活性物质质量均为2.36mg，性能参数较为一致，采样步长设为10s，整体实验方案分为3个阶段：

第一阶段将两枚新锂离子扣式电池A、B串联为电池组PAB（2S1P）进行循环充放电，以1C（0.5mA）恒流充电至4.2V后搁置1min，再以相同电流放电至2.2V后搁置1min视为一个循环，进行50次循环；
第二阶段将一枚新的锂离子扣式电池以4C（2mA）恒流充电至4.2V后再放电至2.2V为一个循环，进行120次循环后替代扣式电池A，构成电池组PB（C2S1P），以1C（0.5mA）恒流充电至4.2V后搁置1min，再以相同电流放电至2.2V后搁置1min，进行50次循环；第三阶段将扣式电池A与一枚新的锂离子扣式电池D串联成为电池组PAD（2S1P）进行循环充放电，同样以1C（0.5mA）恒流充电至4.2V后搁置1min，再以相同电流放电至2.2V后搁置1min视为一个循环，进行50次循环。
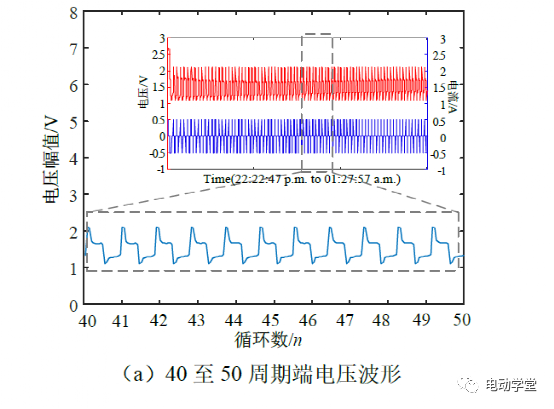
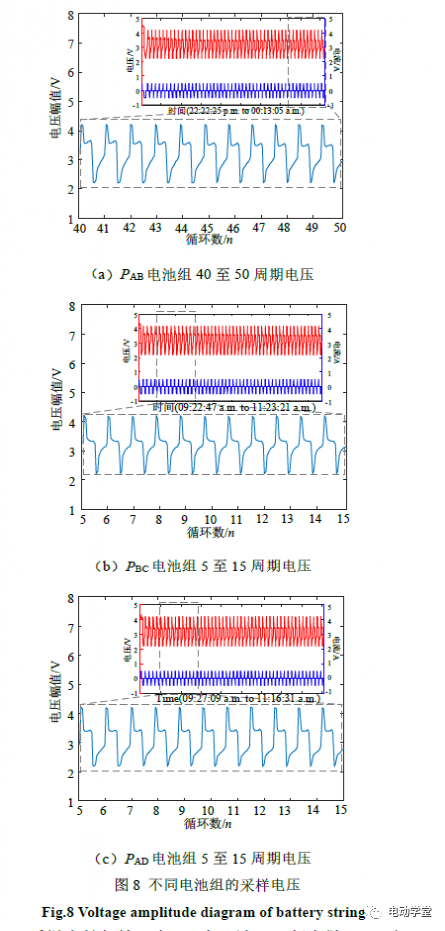
由于循环开始时电池组端电压存在一定程度的波动，因此采样从第5个充放电循环开始：对电池组PAB的40至50周期端电压进行采样，同时对电池组PBC与PAD的5至15周期端电压进行采样。电池组电压波形如图8所示。

采样步长保持不变，对电压波形进行离散处理，各电池组放电过程中存在的瞬间压降幅值ΔUr情况如下图所示。

 
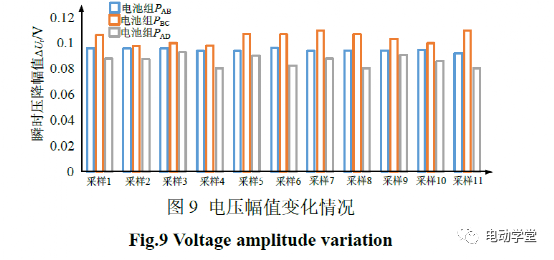
由图9可知，电池组PAB在40次至50次循环放电过程中的瞬时压降幅值ΔUr在0.092V至0.096V范围之内；电池组PBC在5次至15次循环放电过程中的瞬时压降幅值ΔUr在0.10V至0.11V范围之内；电池组PAD在5次至15次循环放电过程中的瞬时压降幅值ΔUr在0.08V至0.09V范围之内。由电压的变化趋势可以看出，如果电池组内某一单体电池的老化程度发生变化，电池组压降幅值ΔUr将增加或减少。以电池PACK箱与电池簇的角度来看，若某一电池PACK箱老化程度发生变化，电池簇压降幅值ΔUr也会相应变化。
3.2变化速率k值分析上述实验中对电池组PAB进行充放电实验，电压变化范围在4.2V至2.2V之间，由于两枚电池性能参数一致，依据分压原理，每枚电池的电压变化范围在2.1V至1.1V之间。因此，为进一步对变化速率k展开分析，对一枚新的锂离子扣式电池E进行循环充放电，以1C（0.5mA）恒流充电至2.1V后搁置1min，再以相同电流放电至1.1V后搁置1min视为一个循环，进行80次循环。所用扣式电池同上节所用电池一样，同批次制出，性能参数一致，因此电池E的充放电数据可以等价于电池组中某一电池的数据，即单体电池E的运行数据可以视为电池组中表征单体的运充放电数据以进行分析。
对单体电池E的40次至50次及55次至65次循环的电压幅值进行采样。

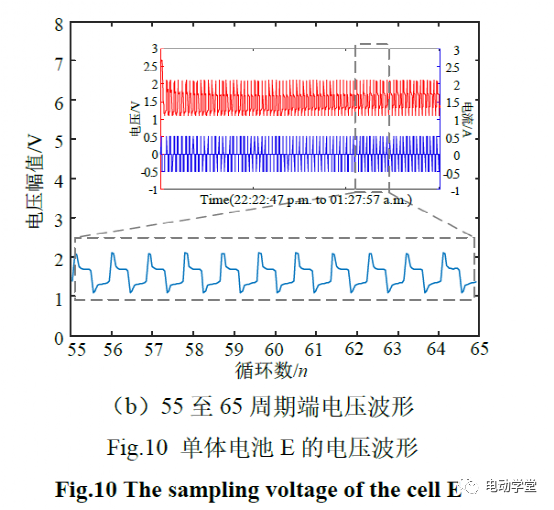
将锂离子扣式电池E的40次至50次循环充放电所测得压降幅值Δur的2倍与电池组PAB的40次至50次循环充放电所测得压降幅值ΔUr进行线性拟合；之后，在上述采样的基础上，将电池E的55次至65次循环充放电所测得压降幅值Δur的2倍与电池组PBC的5次至15次循环充放电所测得压降幅值ΔUr进行逐点线性拟合。拟合结果如图11所示。

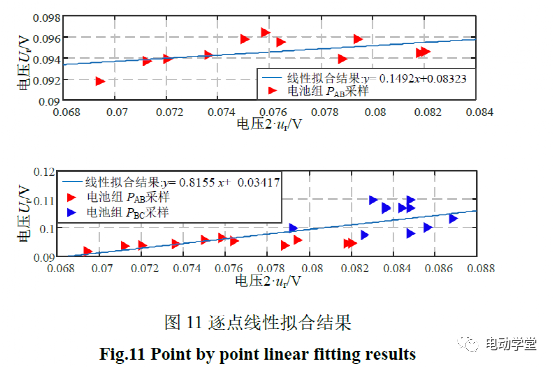
由图中拟合曲线可以看出2·Δur要小于ΔUr，其主要原因是锂离子扣式电池串联在一起，两者正负极并不是完全闭合接触，其存在的空隙一定程度上引起电池组阻抗的增大，导致电压幅值变化的不同。但随着所测数据的逐步线性拟合，线性拟合函数变化速率k由原来的0.1492升至0.8155，存在较为明显的增大趋势。所述实验结果与上节理论分析结果一致，即以电池簇与电池pack箱的视角去看，不一致性的加剧将会导致压降幅值ΔUr与n·Δur差异的逐步增大，变化速率k将呈现增大趋势。
4储能电站实际数据分析
为进一步验证所提不一致性评估方法的有效性，根据湖南省某锂离子电池储能电站1号电池簇11月运行数据进行分析处理。该电池组由20个串联电池组组成，如图12所示，出口处的总直流电压约为768V，放电电流约为90A，且每天恒流充放电各一次。

 
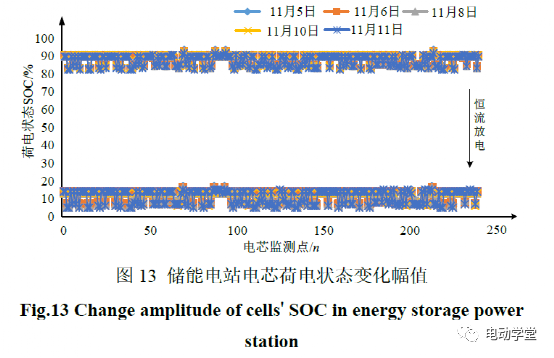
对电池簇任意5天放电过程中电芯SOC变化幅度进行统计，如图13所示。各测量点电芯荷电状态变化幅值ΔSOC集中在73%~75%，即电池簇一致性较好。但数据的采集与存储量显而易见的庞杂。

因此，采用本文提出的方法进行分析处理，根据工作温度对电池组进行筛选，选择1号电池箱作为表征单体。对该电池簇与表征单体11月份任意八天放电过程中的瞬时压幅值降进行采集，如下表所示：

 
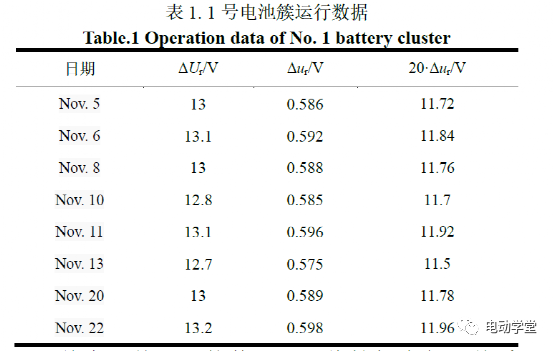
首先对前五天的数据进行线性拟合得到关系f(20Δur，ΔUr)，然后将剩余三天的数据按日期顺序进行逐日拟合，结果如图14所示。

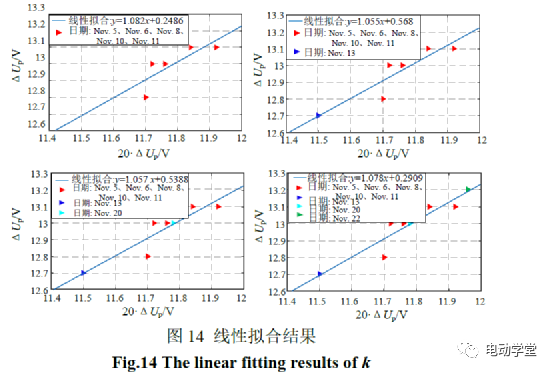
根据实验结果，k稳定在1.05~1.08范围内，可近似于恒定，即1号电池簇一致性好。该结果与大量电芯荷电状态变化幅度ΔSOC的统计分析一致，与传统方法相比，本文所提方法数据的采集与存储量显著减少。
5结论
电池簇安全性与内部电池pack箱运行状态直接相关，为保障储能电站电池簇的安全运行，本文将欧姆内阻的增量作为因子，提出一种基于欧姆内阻压降的电池簇不一致性在线评估方法，通过理论分析与实验验证，得到如下结论：
（1）若电池簇内某一pack箱老化程度发生变化，会造成其瞬时压降幅值ΔUr的增大或者减小；
（2）获取电池簇与表征单体因欧姆内阻造成的压降幅值并进行实时拟合得到线性关系f(n·Δur)=ΔUr，并求导得到变化速率k(n·Δur)=ΔUr，对变化速率k进行在线记录可以实现对电池簇一致性的在线监测。
随着大数据处理技术的不断发展，数据驱动方法持续完善，因此后期将对经验与拟合方法在储能系统的综合应用展开更进一步地研究，以提升储能电池监测技术水平。