非稳态风噪声传递的瞬态SEA模型

摘要

车企的报告显示，乘客对乘员舱风噪声的感知与外部气动声学风荷载的非高斯和非稳态特性密切相关。目前已经有研究表明，尖峰非高斯载荷（峰度κ>3）可以通过非稳态调制高斯随机载荷来合成。本文介绍了一种非稳态气动振动声传输的瞬态统计能量分析（SEA）模型，该模型采用了相同的方法，即在每三分之一倍频程内调制高斯随机脉动压力载荷。作者之前已经表明，随机风荷载的非稳态特性可以在风洞中或道路上进行测量。本文回顾了非稳态外部风噪声传播的瞬态SEA模型和预测调制频率响应函数的公式。然后，利用非稳态风噪声试验数据，将外表面压力的调制统计量与内部风噪声响应的调制统计量相关联，以证明该模型的有效性。

介绍

最早对车内风噪声的研究也认识到，声音的非稳态阵风或振动特性对于人对风噪声音品质的感知有着很大影响。随着气动声学风洞的引入，一些研究人员研究表示，风洞中随机风噪声的统计分布可能与道路上经历的非稳态随机风噪声特征存在显著差异。因此，许多汽车公司已经在其风洞中增加了“湍流生成系统”，以更好地复制道路上经历的非稳态随机湍流载荷。气动噪声界仍未对哪些外部风特性导致了内部风噪声的瞬态特性达成共识。Watkins等人多年来一直在研究这一课题，并确定了两个可能的来源——大规模大气湍流的波动（受路边障碍物的影响）和上游车辆的湍流尾迹。Riegel等人已经证明，这些非定常风噪声源包括偏航角和自由流速度的强烈波动。存在几个量化人对风噪感知相关的指标。第一种是响度，它将1/3倍频程的声级转换为感知临界带，以结合听觉的“掩蔽”效应。粗糙度和波动强度是根据调制幅度和调制频率计算出的声音感知调制强度的细微不同度量。Blommer等人提出了一种用于人类感知阵风和抖振风噪声的脉冲噪声度量。该度量采用1/3倍频程风噪声的时间包络，转换为Barks中的屏蔽响度包络，并使用水平阈值算法对主要脉冲风噪声事件进行计数和表征，并将加权积分到单个度量中。在测试中，Blommer的脉冲风噪声指标与人对抖振风噪声的感知比响度或波动强度指标具有更强的相关性。作者之前已经表明，随机风荷载的非稳态特性可以在风洞中或在道路上使用合适的表面压力传声器测量。利用每三倍频程内压力脉动幅值的希尔伯特变换，比较了外部脉动表面压力（FSP）和内部声压级（SPL）的调制时程。Bremner随后假设，外部FSP风荷载的测量调制可作为瞬态统计能量分析（SEA）模型的输入，以预测内部风噪声。这种非稳态风噪声传播的瞬态SEA模型最近在气动声学风洞中的全尺寸量产汽车上进行了验证，该模型同时应用了气流速度调制和偏航角调制。这些最新的发展是汽车风噪工程向前迈出的重要一步。当输入瞬态SEA声学模型时，在风洞中油泥模型上进行外部FSP测量，可以在开发的最早阶段预测新气动设计的非稳态风噪声声质量。虽然计算流体动力学（CFD）建模作为油泥模型风洞试验的一种替代方法正受到热烈的评价，但CFD可能不容易扩展到预测导致风噪声非稳态音质的外部FSP荷载。首先，完全解决1-8 kHz频率范围内湍流的CFD模型在计算上非常昂贵，因此有用的压力时域结果通常只在非常短的时间间隔（几分之一秒）内可行。由于非稳态风噪声调制已被证明是低频的部分能量在2-25 Hz频带内，因此需要至少5秒（最好是30-60秒）的压力时间历程。其次，风噪声载荷中的低频调制被认为是由入射风中的大型湍流涡流结构产生的，与车身形状相互作用。对于生产风噪工程应用，完全解析的1-8 kHz湍流的CFD模型难以实现。本文介绍了一些早期结果，旨在用实际道路试验数据评估所提出的方法。第一节描述了道路试验数据样本的收集以及外部FSP与内部SPL的观察统计特性。第二部分讨论了非稳态风噪声的统计特性以及所提出的调制模型的适用性。第三节简要回顾了如何在瞬态SEA模型中使用实测FSP调制数据来预测内部风噪声调制。第四部分使用瞬态SEA模型预测的调制频率响应函数来描述调制从外部到内部的传输。第五节将瞬态SEA模型应用于道路试验车辆，对模型的有效性和非稳态内部风噪声统计特性的可能机制得出结论。

道路风噪声数据统计

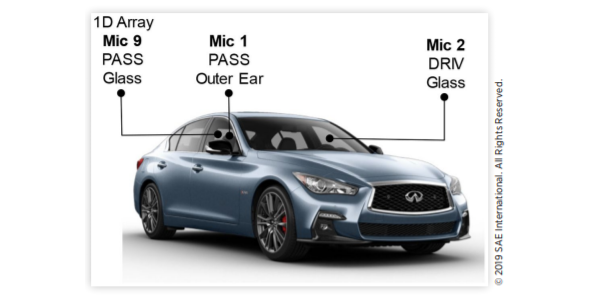
在图1所示的量产轿车上，对驾驶员侧玻璃和乘客侧玻璃上的外部脉动表面压力（FSP）以及乘客外耳处的内部声压级（SPL）进行了同步测量。作者采用的64通道MEMS数字表面话筒阵列位于乘客侧玻璃上部的A柱涡流区，如图2所示，在该区域通常可以观察到较高的FSP水平，尤其是在非零偏航条件下。

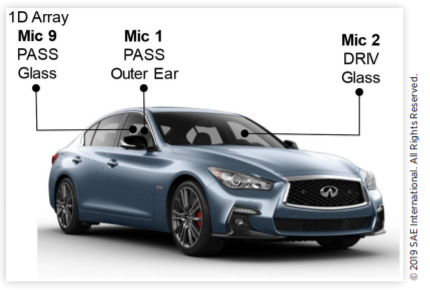
图1 用于测量道路风噪声统计特性的麦克风

该阵列在前两个麦克风上使用了延长的电线。如图2所示，这允许麦克风1位于乘客外耳，通过阵列在靠近侧玻璃外部FSP测量的直接声场中测量内部SPL。阵列话筒9用作乘客侧玻璃外部FSP统计特性的代表性样本。

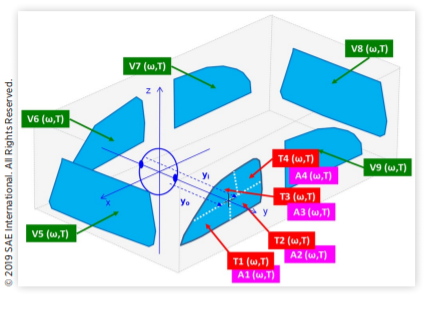
图2 麦克风9测量乘客侧玻璃上的FSP，麦克风1测量乘客外耳处的SPL

在与麦克风9相同的位置，在驾驶员侧玻璃上，使用阵列麦克风2测量车辆另一侧的外部FSP，如图3所示。

图3 阵列话筒2测量驾驶员侧玻璃上的FSP，与话筒2对称

在南加州的一条高速公路上，在没有其他车辆靠近的情况下，首次在空气动力学静态条件下，在三种不同的道路速度下进行了道路风噪声测量。为了区分风噪声和道路轮胎噪声，缩放mic 1处内部SPL的自动频谱，以找到所有测量值塌陷到相同频谱的道路速度指数。图4中的速度缩放结果表明，在800 Hz以下，指数约为3，这是典型的道路轮胎噪声。在800-2500 Hz的频率范围内，观察到较高的速度标度指数为6-8，这表明存在风噪声。高于2500 Hz时，内部声压级过低，麦克风1信号接近仪表噪声下限，无法使用测试数据。本文讨论的所有后续道路试验结果仅适用于风噪声主导的频率范围800-2500 Hz。

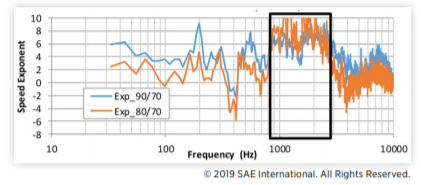
图4 缩放SPL自动频谱所需的道路速度指数

非稳态风噪声测量是在大型车辆尾迹速度范围内进行的，如下表1所示。

表一 风振测量条件

在800-2500 Hz的频带内过滤麦克风数据，并计算每个测试中每个麦克风信号的前四个统计时刻。所有测量的平均值（第一时刻）均为零。标准偏差（第二时刻）是每个麦克风的预期RMS。偏斜度（第三时刻）很小，可以忽略所有测量，包括外部FSP和内部SPL。尖削度（第四时刻）——表明随机压力信号的冲击性——在测试之间以及外部FSP和内部SPL信号之间表现出显著差异，如图5所示。

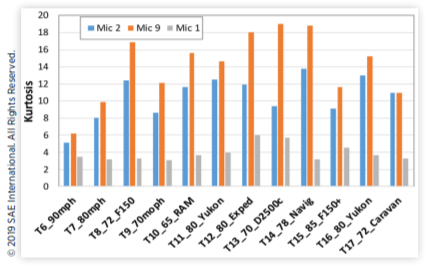
图5 在800-2500 Hz的风噪声频带内，测得的麦克风信号的峰度

最显著的趋势是，内部风噪声的峰值总是显著小于外部表面压力。正如预期的那样，静态试验6、8和9的外部FSP峰度低于其余抖振环境试验的峰度。Mic 2的峰度始终低于Mic 9。这一趋势被认为是由于不同的挡风玻璃的原因（Mic 9为开放端口，无挡风玻璃）。高斯（“正态分布”）随机信号的峰度为3，可以看出，所有外部FSP信号的峰度都显著大于3，表明为非高斯随机压力。在洁净空气条件下，内部SPL的峰度接近3，但在受到上游车辆抖振尾迹的影响时，可以增加到4-6。图6中mic 9外部FSP的直方图清楚地显示了压力分布上的强脉冲“尾”，对应于高峰度。值得注意的是，清洁空气（测试T7）的分布似乎也是强非高斯分布。

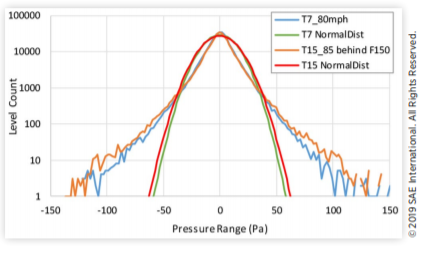
图6 干净空气试验7和非静止尾迹试验15的mic 9外部FSP直方图，叠加在高斯（正态）分布上

图7中mic 1内部SPL的相应直方图证实了洁净空气条件下的内部SPL是高斯随机的。对于非稳态尾迹条件（测试T15），内部SPL上的峰度增加，变得更加弱非高斯。

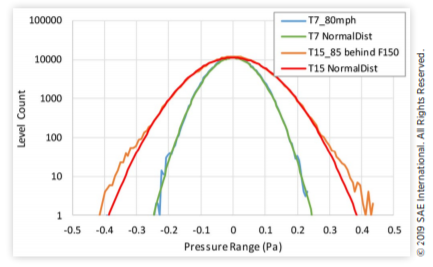
图7 干净空气试验7和非静止尾迹试验15的mic 1内部SPL直方图，叠加在高斯分布上

与外部气动声压传输到内部声学声压级相关的随机压力信号统计特征发生这种实质性变化的原因尚不清楚。本文将使用非稳态风噪声传输的瞬态SEA模型来评估影响观测行为的两种可能机制。

非稳态风噪模型

在车辆振动的非稳态路面输入情况下，Rouillard和Sek表明，非高斯“轻量级”载荷（峰度κ>3）可以通过非稳态调制高斯随机载荷来合成。他们表明，非稳态和非高斯过程可以建模为一系列具有不同持续时间和RMS水平的i高斯随机段（κ=3）。整体峰度κ可以表示为序列分布和相应prms水平的函数。

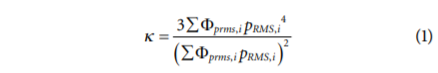
Watkins等人和其他研究人员报告了内部风噪声的类似非稳态随机特性。一种常见的方法是使用希尔伯特变换来定义每三分之一倍频程频带中的时变“调制包络”，如图8所示。作者还测量了引起内部风噪声的外部脉动表面压力（FSP）的调制。图9显示了存在非稳态上游尾流时的典型调制谱图。如图8（右）中的蓝线所示，对于FSP的每三个倍频程频带，调制频谱是调制包络时间信号的傅里叶变换。正如其他研究人员所观察到的，非稳态风噪声调制是低频的，大部分能量在2-25 Hz频段。

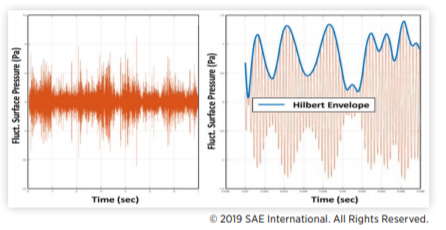
图8 非稳态、非高斯风噪声（左）建模为第三倍频程中高斯随机载荷的振幅调制（右）

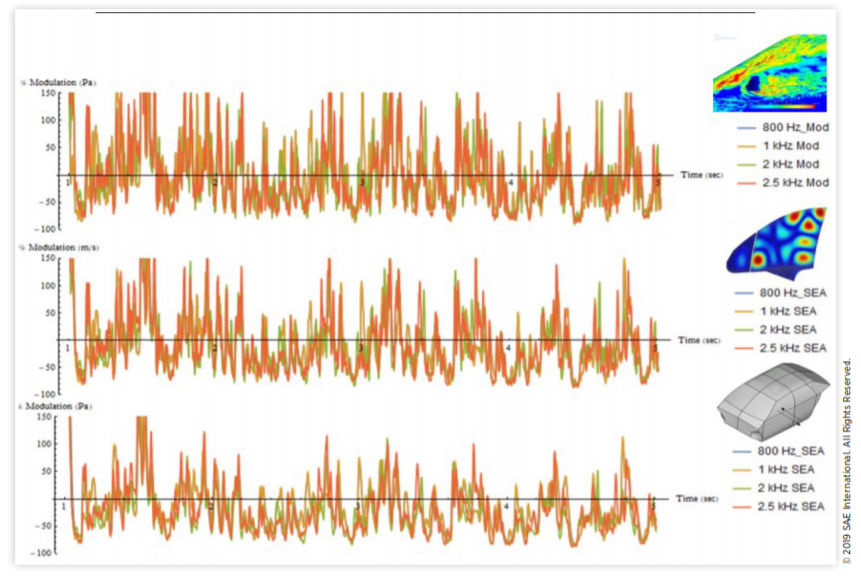
图9 非定常尾流条件下外部FSP的典型调制谱图傅里叶频谱中的每条频率线ωk可被视为调幅（AM）信号，例如：

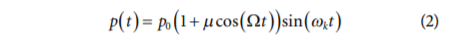
其中p0是频率ωk处载波信号的峰值振幅，μ是调制振幅比，Ω是调制频率。公式（2）的傅里叶变换表明，调制为载波信号增加了边带。与未调制载波信号相比，调制边带增加了RMS电平：

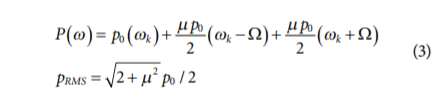
公式（1）中（2）的近似积分证实，增加高斯随机数据的调制比μ会导致峰度增加，如图10所示。

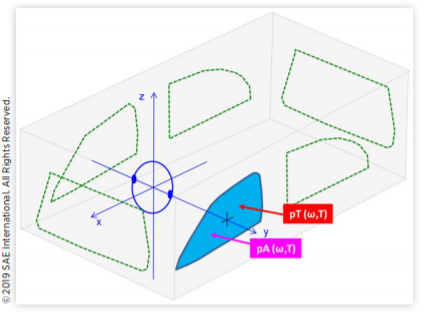
图10 调制高斯随机信号的峰度预测

瞬态风噪SEA模型

本文评估了Bremner提出的非稳态风噪声瞬态统计能量分析（SEA）模型。图11和图12对模型进行了示意性总结。对于稳态随机风噪声，外部风荷载由对流湍流和外部声学的压力自谱建模。然而，对于非稳态风噪声，每个第三倍频程频率带ωk中的波动压力水平被视为调制时间T的函数。侧玻璃共振的直接功率输入和内部座舱声学模式的间接功率输入（通过非共振玻璃振动响应传输）是时间T的函数。

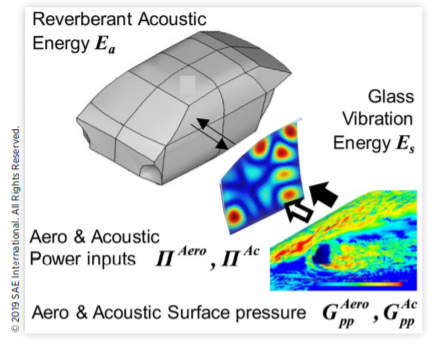
图11 风噪声传播模型示意图

图12 非稳态风噪声向车内传播的相应瞬态SEA模型空间平均玻璃振动响应的调制包络与玻璃共振振动模式中的能量成正比，而车辆内部的混响声压级与座舱共振声学模式的能量成正比。在瞬态SEA模型中，这些时变能量是根据每个子系统的功率平衡方程矩阵计算的。对于图12中简单的两个子系统模型，瞬态SEA平衡方程形成一对一阶微分方程。

对于风噪声荷载的一般希尔伯特时间包络，这些方程可以用数值方法求解。

调制传输频率响应函数

图13所示的瞬态SEA模型已成功用于验证全尺寸量产汽车在气动声学风洞中的非平稳风噪声传播模型，该风洞具有受控的周期风速和受控的偏航角。整车SEA模型使用测得的驾驶员玻璃负载外表面压力（FSP）调制时程，以及测得的振动调制时程来估计风噪声通过其他玻璃表面传播的贡献。对SEA模型进行了扩充，以预测每个玻璃的混响和直接场声压级，并包括用于预测乘员外耳和内耳位置声压级的头部散射效应。

图13 在风洞测试的全尺寸汽车瞬态SEA模型。

模型1-侧面玻璃上的相干调制

上述调制传输频率响应函数衰减更高调制频率Ωm的趋势，为外部FSP与内部SPL的道路峰度之间的显著差异提供了一种可能的解释。根据方程式（1）和图10，外部FSP中高频调制的大幅度将有助于获得较高的峰度值。如果高频调制的传输因侧窗共振的混响时间和座舱声学模式的混响时间而显著衰减，则内部声压级的非高斯峰度应显著降低。使用道路试验车辆的简单瞬态SEA模型来评估这一假设。图14中的模型将道路上测量的调制湍流载荷和外部声学载荷的单相相干区域应用于侧玻璃。直接（共振玻璃振动）和间接（非共振玻璃振动）传输路径均按照方程式（4）和（5）建模。

图14 瞬态SEA模型1用于评估测量的道路FSP调制到内部SPL调制的传输，假设侧玻璃上存在相干调制

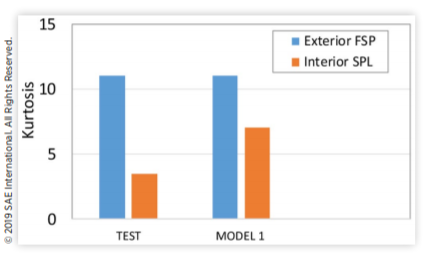
图15 风噪声峰度的比较表明，模型1无法预测测量到的内部SPL峰度降低

图16（上部）显示了测试15中样品第三倍频程频带内道路测量的外部FSP调制时间历程。调制以规范化的“%modulation”格式显示。中间的图表显示了侧面玻璃振动的百分比调制响应，由瞬态SEA模型预测。下图显示了瞬态SEA模型预测的内部SPL的调制响应百分比。仔细检查发现，根据调制频率响应函数、方程（9）和（10）预测，玻璃振动和内部风噪声SPL的调制百分比降低。图10中估算的内部SPL的相应峰度与图15中的测试结果进行了比较。很明显，调制衰减不足以解释道路测量中观察到的近高斯内部SPL峰度的转换。

图16 外部FSP（上部）的实测调制和侧玻璃振动（中部）和内部SPL（下部）传输调制的模型1预测；对于四个三倍频程频段，其中道路风噪声占主导地位。

模型2-侧玻璃上的不相干调制

作者之前在道路和风洞上进行的测量观察到，侧玻璃上的外部FSP调制没有完全相关。假设风噪声调制源和传输路径之间的相关性不完全，这是一种额外的机制，有助于将非高斯外部FSP转换为近高斯内部风噪声SPL。瞬态SEA模型用于检验这一假设。外部气动声学加载中的完全相关调制用四个不同的湍流和外部声学加载区进行建模，如图17所示。通过两种方式模拟了预期的调制去相关效应。首先，将从车辆另一侧玻璃测得的FSP用于较低玻璃T1、A1负载，以模拟部分不相关的后视镜尾迹调制。其次，通过对前向玻璃加载T1、A1和T3、A3分别施加对流时间延迟来模拟后玻璃加载区T2、A2和T4、A4。

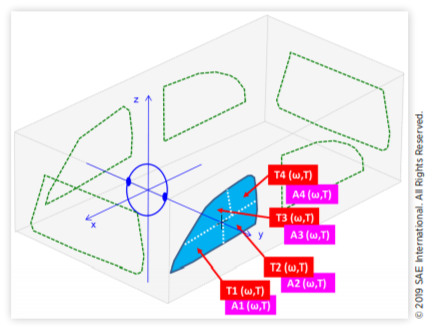
图17 瞬态SEA模型2用于评估测量的道路FSP调制到内部SPL调制的传输，假设侧玻璃上有四个部分相关的调制加载区。图18（上部）显示了测试15中对象3倍频程频带中四个道路上测量和模拟的外部FSP调制时间历程。中间的图表显示了侧面玻璃振动的百分比调制响应，由瞬态SEA模型预测。下图显示了瞬态SEA模型预测的内部SPL的调制响应百分比。

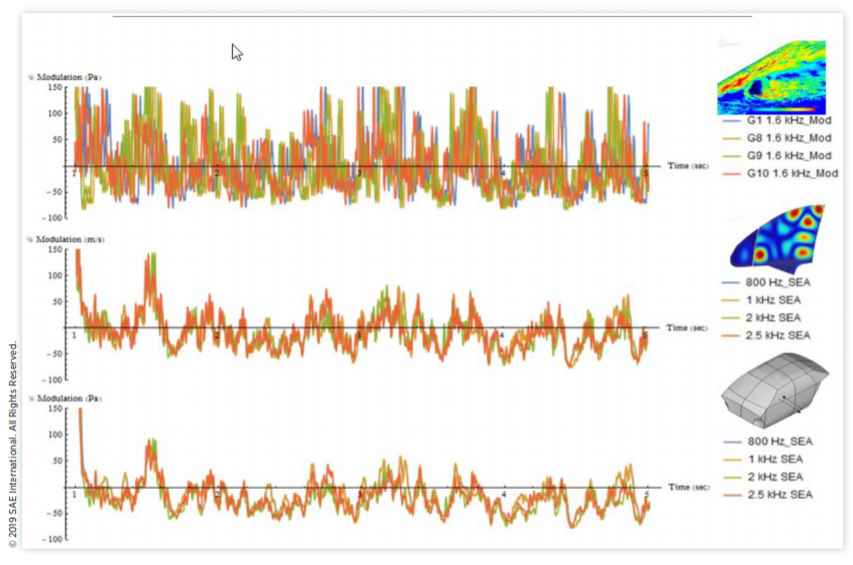
图18 外部FSP荷载四个区域的测量和模拟调制（上部），以及侧玻璃振动（中部）和内部SPL（下部）传输调制的模型2预测；对于四个三倍频程频段，其中道路风噪声占主导地位在这种情况下，与外部气动声学载荷的百分比调制相比，玻璃振动和内部风噪声SPL的调制显著减弱。使用图10将模型1和模型2的预测内部SPL调制结果转换为峰度。图19中的结果证实，模型2与道路测量的峰度趋势相比更好。

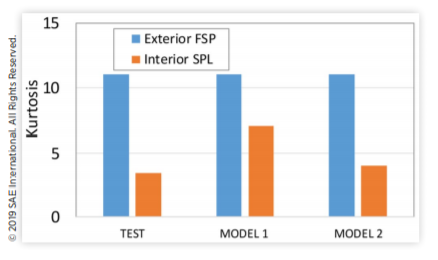
图19 模型2预测从外部FSP到内部SPL的峭度降低，与测试一致作者认为，这一结果与中心极限定理一致，中心极限定理指出，具有不同概率密度函数的足够大的信号之和将始终收敛于高斯正态分布。在道路上的汽车中，与图16中非常简单的瞬态SEA模型中的有限噪声源相比，内部风噪声调制的影响因素可能更多。在这种情况下，将有更多的传输调制的“取消”和更强的收敛到近高斯内部SPL。

讨论

汽车制造商报告称，乘客对车辆内部风噪声的感知受到外部气动声学风荷载的非高斯和非稳态特性的影响。可以说，定义适当的音质指标和定义噪声工程设计程序以实现这些指标是一个挑战。

最近，高分辨率表面压力阵列与瞬态SEA模型一起使用，为应对这些挑战提供了新的、更强大的技术基础。这些方法具有严格的数学基础，并已在受控周期风调制风洞中得到验证。本文介绍了在非稳态风噪声驱动条件下，将瞬态SEA模型与实际道路风噪声测试数据进行关联的初步结果。很明显，更严格的验证可能很困难，但使用现有的新工具肯定是可能的。这些新的发展可能是汽车风噪声工程向前迈出的重要一步。当输入瞬态SEA声学模型时，在风洞中油泥模型上进行适当的外部FSP测量，可以在开发的最早阶段预测新气动设计的非稳态风噪声声质量。虽然计算流体动力学（CFD）建模作为油泥模型风洞试验的一种替代方法，但CFD可能不容易扩展到预测导致风噪声非稳态音质的外部FSP荷载。首先，完全解决1-8 kHz频率范围内湍流的CFD模型在计算资源上非常昂贵，因此有用的压力时域结果通常只在非常短的时间间隔（几分之一秒）内可行。由于非稳态风噪声调制已被证明是低频的-大部分能量在2-25 Hz频带内-需要至少5秒（最好是30-60秒）的压力时长。其次，风噪声载荷中的低频调制被认为是由入射风中的大型湍流涡结构产生的，与车身形状的空气动力相互作用。对于生产风噪声工程应用，完全解析的1-8 kHz湍流的CFD模型（跨越整车空气动力学和上游湍流尾迹发生器的尺寸）可能是无法实现的。

结论

采用时间同步的外部脉动表面压力（FSP）和内部声压级（SPL）测量来量化上游车辆尾迹中行驶时风噪声的非稳态和非高斯特性。测量结果表明，外部FSP表现出高水平的统计峰度，这可以描述为第三倍频程频带中高斯随机压力波动的非稳态调制。当相同的风噪声传输到乘员舱时，内部SPL显示出明显较低的峰度水平。该非稳态风噪声统计模型与瞬态SEA模型兼容，该模型可以预测从外部FSP到相应玻璃振动调制和内部SPL调制的调制传输频率响应函数。本文利用瞬态SEA模型表明，统计峰度的降低可能有两个联合效应。主要影响是不相关（或仅部分相关）的多个风噪声源和/或路径贡献的总和。第二个影响是调制传输频率响应函数中的自然衰减和相位延迟，这归因于共振玻璃振动的混响时间和座舱声学模型的混响时间。

这些新工具的进一步验证有望帮助理解需要考虑的气动声学设计参数，以避免非稳态随机气动声学引起的风噪声音品质问题。

文章来源：

Bremner, P.;Clifton, S.;Todter, C..A Transient SEA Model for Transmission of Non-Stationary Wind Noise(Conference Paper)[J].SAE Technical Papers,2019,Vol.2019

AutoAero是吉林大学张英朝教授团队建立的专业汽车空气动力学微信公众号号，致力于普及汽车空气动力学知识，传播汽车空气动力学。推广包括流体力学基本理论，汽车空气动力学及热管理水管理等基础知识，乘用车气动造型设计，卡车气动造型设计，风洞实验技术等多方面的内容。欢迎有兴趣的专业人士阅读、关注、共享！