基于NSGA-Ⅱ算法对发动机噪声激励下的整车声学包优化

摘要：通过整车声学包合理设计能有效的改善发动机传至车内的噪声。基于统计能量法，利用Hypermesh 和VA One软件搭建整车SEA 模型，对比测试与仿真分析的PBNR 值验证模型的精度。前围板作为发动机到驾驶室的主要传递路径，以前围内外侧声学包材料的厚度、属性、堵孔件厚度及声学材料覆盖率为自变量，利用创建的SEA 模型得到主驾右耳的PBNR 值、声学材料的总质量及总价格并作为响应。在MATLAB 中建立自变量与响应间的数学模型，对各响应赋予一定权重，利用非支配排序遗传算法（NSGA-Ⅱ）获得Pareto 最优解。通过SEA 模型分析最优解及任意三组Pareto 解的响应，验证最优解的可信性；对比原声学包响应：PBNR 值提高2.0dB、总重量降低8.5%、价格降低3.6%。分析表明，通过对SEA 模型进行PBNR 分析结合NSGA-Ⅱ算法能快速得到整车的最优声学包设计方案。

1 引言

在汽车怠速及行驶时，发动机噪声对车内NVH 性能有重要影响。研究表明，合理的前围板声学包设计能够在不改变整车骨架结构的前提下有效降低车内中高频噪声，改善用户对整车NVH 性能体验。国内外很多学者对汽车的声学包设计做了诸多研究。文献基于统计能量分析（Statistical Energy Analysis，SEA）在控制总质量与成本的前提下进行声学包优化设计并获得最优方案。文献基于正交设计理论，借助VA One 分析软件对汽车声学包进行优化设计，有效改善了车内声压级。该类方法在进行整车声学包设计时受试验条件限制且试验成本高，难以保证得到的离散最优试验结果为最优方案。文献基于SEA 模型进行声学包性能分析，通过试验改进声学包方案。该类方法针对现有问题解决时快速有效，但对正向开发声学包的最优设计问题指导性差。文献以前围板的声学包隔声量及重量为优化目标，借助ISIGHT工程软件创建近似拟合模型并通过软件自带的Optimal 模块进行寻优并获得最优设计。该类方法更适用于子系统、优化目标较少的声学包设计，但随着整车声学包问题研究时研究目标的增多，优化过程会变的较为复杂且难以得到优化解。文献结合正交试验设计与灰色关联分析，进行声学包裹材料种类及厚度的确定，通过构建Krging 近似模型，以降噪、减重为响应，采用多目标粒子群算法（MOPSO）获得最优的声学包设计。该方法中MOPSO算法在全局寻优时容易陷入局部最优、收敛精度有限和解集分布不均匀。在VA ONE 中搭建（250～10000）Hz 频段的整车SEA 模型，对试验与仿真进行基于能量的隔声量（Power based Noise Reduction，PBNR）分析，验证有限元分析模型的精度。针对发动机噪声激励，以前围内外侧声学包材料的面密度、材料厚度、过孔堵件厚度及覆盖率为自变量，以PBNR 值、声学包质量和声学包成本为因变量在MATLAB 中搭建Kriging 模型，采用NSGA-Ⅱ算法进行多目标优化得到最优声学包组合方案，通过搭建的SEA 模型验证方案的可信性。

2 整车SEA 模型建立及验证

2.1 整车SEA 模型建立

基于统计能量（SEA）的分析方法是结合统计学和有限元分析的方法，是有效解决中高频段声学包分析的重要手段。在Hypermesh 中搭建待分析的车身有限元模型，根据SEA 模型建模原则在VA ONE 软件中搭建的整车SEA 模型，如图1 所示。

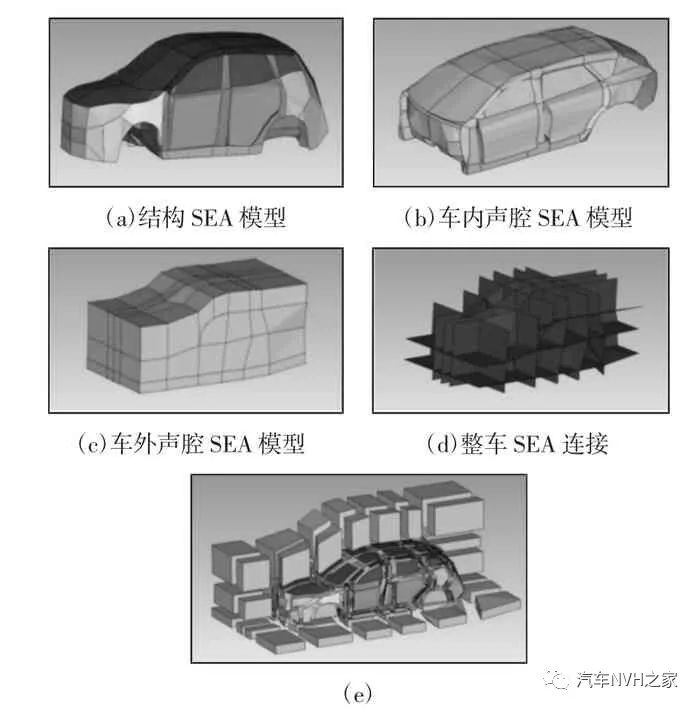
图1 整车SEA 模型
Fig.1 SEA Model of the Whole Vehicle图1（a）为整车的结构子系统SEA 模型，根据车身材料属性、厚度、阻尼及曲率对结构钣金进行子系统划分，共创建614 个板件子系统；图1（b）为整车车内声腔SEA 模型，按左右对称原则对前排、后排、行李舱进行划分，区分驾驶员与乘员的头部、腰部及腿部声腔，共划分为40 个车内声腔子系统；图1（c）为整车车外声腔SEA 模型，按左右对称原则在车外表面至1000mm 范围创建车外声腔，共生成96 个车外声腔子系统；图1（d）为整车车内各子系统声腔间的SEA 连接形式，为保证各个子系统间能量的传递，各板子系统与声腔子系统间选择面耦合形式连接，各板子系统之间选择线耦合方式连接，在线与线交汇处选择点耦合的方式连接，共生成1079 个连接。整车SEA 模型的关键声学包参数（耦合损耗因子、内损耗因子和模态密度等）均可通过设备测试或理论计算获得，具体不再详述，如图2 所示。

图2 模型材料属性测试设备
Fig.2 Model Material Property Test Equipment

2.2 整车试验测试及仿真模型验证

基于能量的隔声量试验技术（Power based Noise Reduction，PBNR）常用于衡量声学包的性能，PBNR 指点声源的声功率与测点声压平方的比值，是1/3 倍频程频率的函数，其对数形式表达式为：

在整车半消室内测试实车在发动机怠速噪声激励下，驾驶员右耳附近的声压响应，如图3 所示。对测试结果进行PBNR 分析，分析结果，如图5 所示。

图3 整车PBNR 测试示意图
Fig.3 PBNR Test Diagram of the Whole Vehicle在VA ONE 软件中对创建的SEA 模型进行整车PBNR 分析，如图4 所示。在半消声室环境边界下在发动机激励处施加1W 声功率激励，分析（250～10000）Hz 频率范围的驾驶员右耳处的声压响应并做PBNR 分析，仿真的PBNR 分析结果，如图5 所示。对比仿真与测试的发动机激励到驾驶员右耳的PBNR 结果，由图5 可知在（250～10000）Hz 整个分析频段内仿真与测试的差值在±2.5dB 内，说明搭建的SEA 仿真模型满足后续工程分析精度要求。由于试验的边界是近似自由的，而仿真模型的边界条件是完全自由的，边界条件的不完全一致，因此在分析频段内测试值略小于分析值。

图4 整车PBNR 仿真分析示意图
Fig.4 Schematic Diagram of PBNR Simulation Analysis of the Whole Vehicle

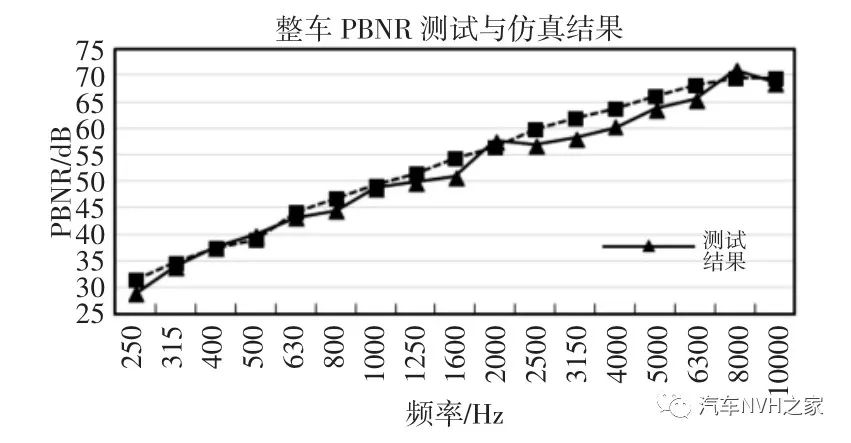
图5 整车PBNR 测试与仿真结果
Fig.5 PBNR Test and Simulation Results of the Whole Vehicle

2.3 声学包优化子系统确定

结合现有研究并对基础车的SEA 模型进行发动机噪声激励下的各传递路径对驾驶员头部声腔功率贡献量分析可知，机舱前围能有效吸收和阻隔发动机舱辐射到车内的主要能量，且由于铺设面积大、质量也较大，优化空间大，优化效益明显，因此选择对前围内外侧声学包进行优化。选定常用声学包装材料种类以前围内外侧声学包的面密度、厚度、覆盖率、堵件厚度为优化变量，考虑声学包裹在满足主要的降噪性能同时还需兼顾整车轻量化设计及直接经济成本，对发动机噪声源到驾驶员右耳处的PBNR值、声学包总质量、声学包总成本为目标进行优化。

3 声学包优化模型建立及验证

3.1 试验点设计

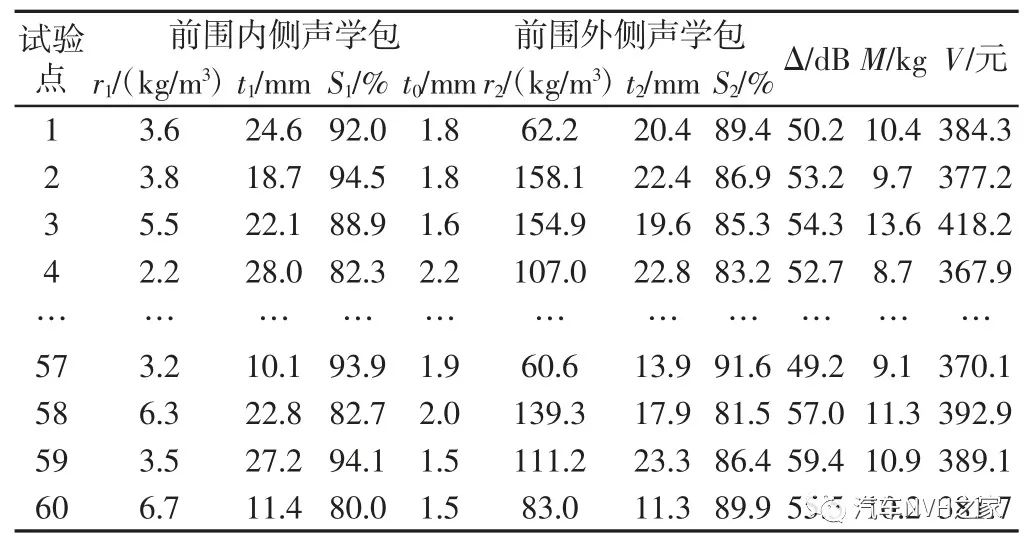
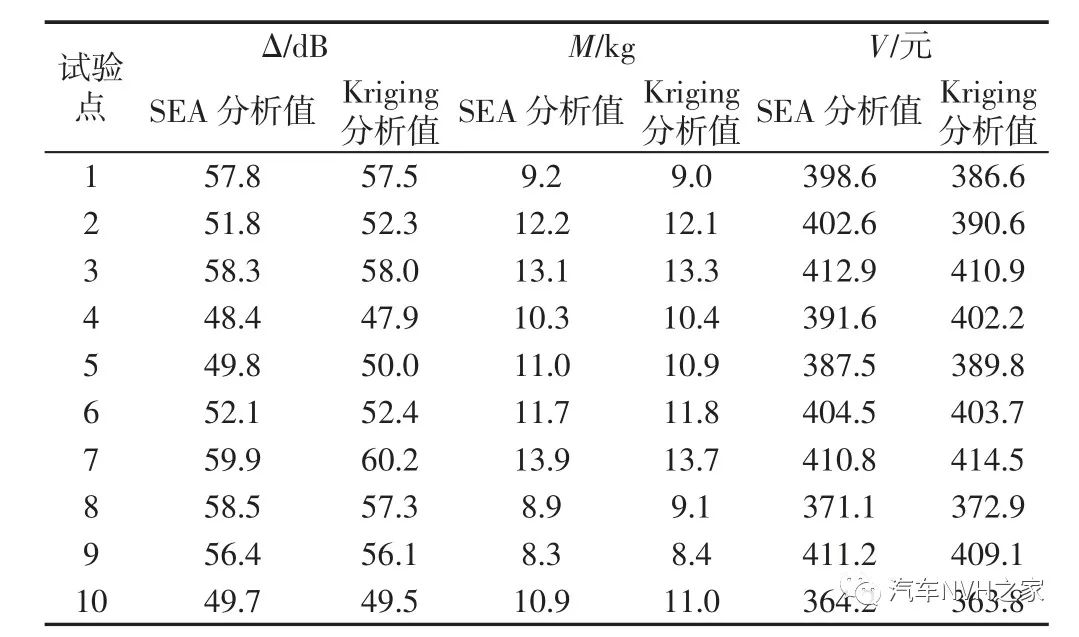
针对前围的声学包进行优化时主要对前围内外侧声学包的面密度、厚度、覆盖率及堵件厚度进行优化，各个量在汽车设计前期或者优化前期都属于位于一定区间范围的未知离散量，其取值在所处区间内符合均匀分布。为保证优化结果是遍历区间内所有取值后的结果，所以在进行试验点设计时应使所有变量在各自的取值区间内均等概率的被选取分析。最优拉丁超立方设计作为常用的采样设计被广泛使用，对多变量进行随机抽样时既能保证各变量的均匀性又能很好的填充设计空间，同时对于非线性响应问题有很高的拟合精度，所以通过最优拉丁超立方设计生成试验数据点。前围内隔音材料选择EVA+PU 发泡组合，常用EVA 面密度r1 介于（2～7）kg/m2，根据实际车辆结构限制PU 发泡的厚度t1 介于（10～30）mm。此外PU 发泡的密度65kg/m3，EVA 的厚度为3.5mm，密度为950kg/m3。前围外隔热垫选择PET+轻质PU+PET材料组合，PET 面密度r2 介于（60～160）g/m2，轻质泡棉厚度t2 介于（10～25）mm。此外轻质PU 泡棉的密度为16kg/m3，PET 材料的密度为1370kg/m3。考虑实车声学包布置空间，前围内侧声学材料覆盖率S1 取值设为（80～95）%，外侧声学材料覆盖率S2 取值设为（70～90）%，前围的过孔橡胶堵件厚度t0 取值设为（1.5～3.5）mm。采用最优拉丁超立方设计生成60 组试验点，每组试验点可用SEA 模型分析出发动机噪声激励到驾驶员右耳平均PBNR 值Δ，部分试验样点的分析结果，如图6 所示。由图5 及图6 可知在8000Hz 频率范围内PBNR 与频率呈明显线性关系，故取PBNR结果的平均值作为该试验点的隔声性能。所有试验点的平均PBNR 值Δ 及总质量M、总价格V，如表1 所示。

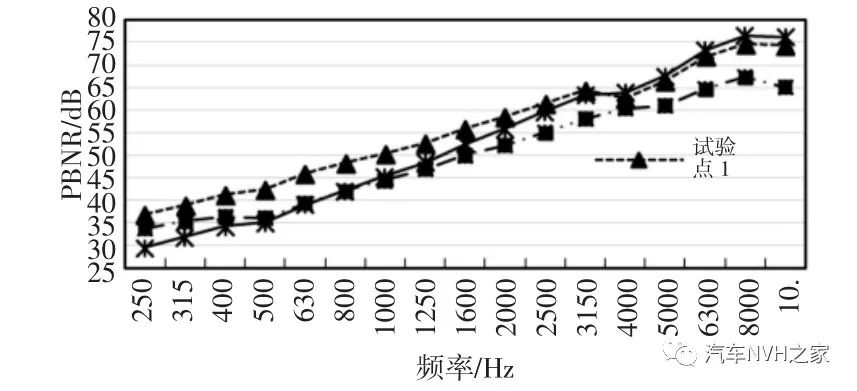
图6 部分试验样点的PBNR 仿真结果
Fig.6 PBNR Simulation Results of Some Test Samples表1 样本点及响应值
Tab.1 Sample Points and Response Values

3.2 克里金模型搭建与验证

为提高优化效率，快速得到前围内外侧声学包参数与声学包隔声性能、总质量、总价格之间的量化关系，提高优化效率，需搭建近似分析模型。克里金（Kriging）模型作为一种估计方差最小的无偏估计模型，具有近似面质量高、样本覆盖面广的优点，故采用Kriging 近似模型来分析。在MATLAB 中借助工具箱dace 函数，创建以EVA 面密度、PU 厚度、PET 面密度、轻质PU 厚度、前围堵件厚度、前围内外层声学包覆盖率以及前地板PET 面密度共七个自变量与PBNR 均值Δ、总质量M、总价格V 为响应的Kriging 模型。为保证近似模型的拟合精度，利用最优拉丁超立方采样另生成10 组试验样点，如表2 所示。结合SEA 模型分析得到数据，如表3 所示。按式2进行相关指数R2 检验。

本Kriging 拟合模型的PBNR 均值、声学包总质量、总价格的R2 值分别为0.955、0.978、0.966，说明近似模型拟合精度高，预测结果可靠。表2 十组验证近似模型精度的试验点
Tab.2 Ten Groups of Test Points to Verify the Accuracy of Model

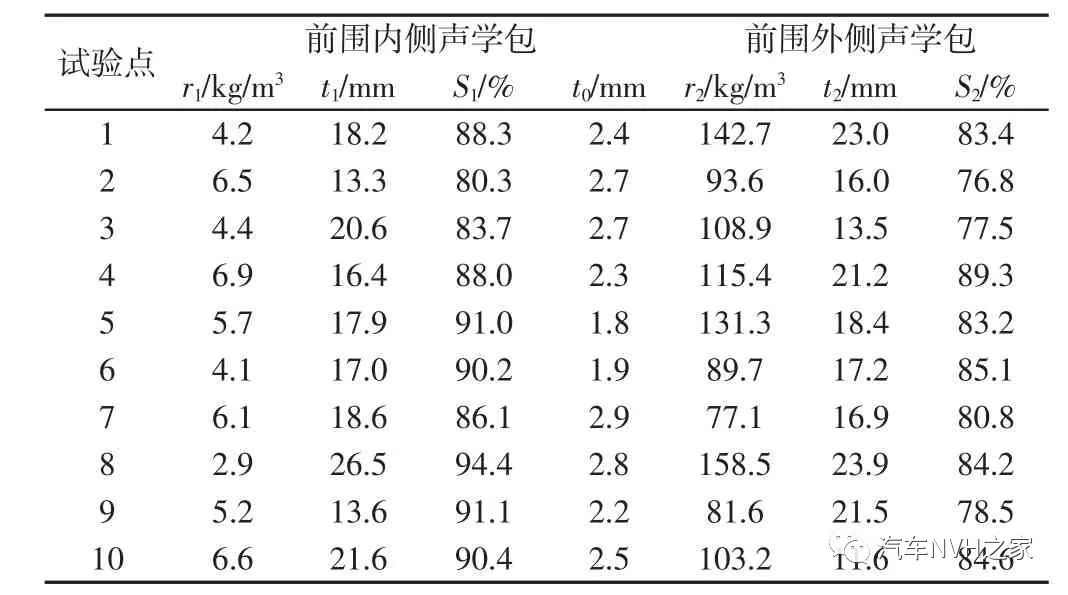
表3 十组试验点的预测结果与分析结果
Tab.3 Prediction and Analysis Results of Test Points

4 声学包的多目标优化

声学包的性能指标往往与成本、轻量化指标相矛盾，所以对声学包的优化本质是寻求三者的平衡，即PBNR 均值Δ、总质量M、总成本V 需满足：

对于多目标优化问题第二代非支配排序遗传算法（Non dominated Sequencing Genetic Algorithm，NSGA-Ⅱ）被广泛应用，在原来NSGA 算法的基础上引入了拥挤度比较算子与精英群策略，既保留了样本中的最佳个体又保证了非劣最优解均匀分布，同时提高了算法的稳定性及运算速度。考虑到PBNR 均值Δ、总质量M、总成本V 三者数量级不同，而NSGA-Ⅱ在进行二进制编码交叉变异时会造成染色体的剧增，故需要在进行遗传操作算子前进行同级归一化处理。

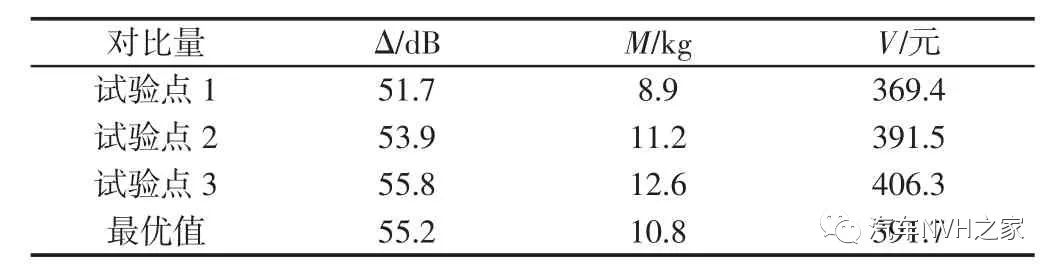
在MATLAB 中编制NSGA-Ⅱ算法，以式（3）为目标进行优化求解，经过500 次迭代，得到Δ、M 及V 之间的帕累托（Pareto）图，如图7 所示。

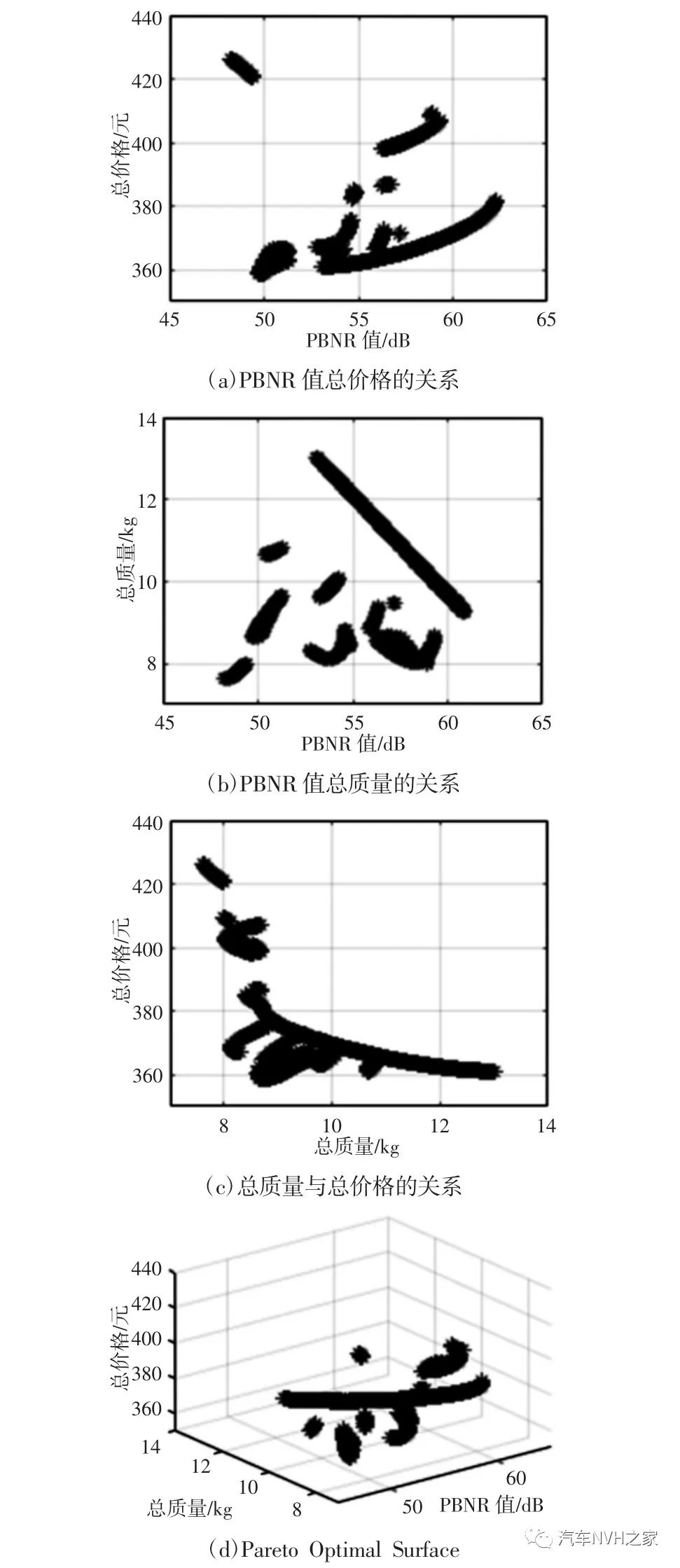
图7 PBNR 与质量及总价之间的帕累托解集
Fig.7 Pareto Solution Set Among PBNR and Quality and Total Price由图7 可知，PBNR 值与总质量、总价格之间属于矛盾关系，在追求降噪性能PBNR 值最大时会产生总价格与总质量的增加，在追求质量最轻时会引起总价的升高及降噪性能的不达标，在追求最低成本时将引起降噪性能的降低、总质量的上升，所以需要在诸多前沿解中寻求降噪性能与成本、造价的最优化方案。为评价各前沿解方案的优劣，对各优化目标赋予一定权重，降噪性能为主要目的，赋予0.4，造价与轻量化对于各主机厂同等重要，均赋予0.3。根据NSGA-Ⅱ算法得到的最优解确定对应的声学包参数，利用搭建的SEA 仿真模型得到仿真结果，如表4 所示。表4 仿真与近似模型分析结果
Tab.4 Simulation and Approximate Model Analysis Results

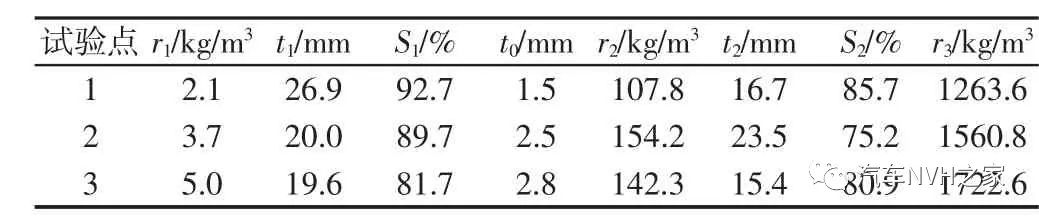
从表4 可知，利用NSGA-Ⅱ算法得到的最优方案对应SEA及Kriging 近似模型的PBNR 均值、总质量、总价格的误差均小于5%，进一步说明Kriging 近似模型拟合效果好，可信度高。任取Pareto 解集中的三组解对应的试验点，如表5 所示。通过SEA 模型得到PBNR 值、总质量、总价格，如表6、图8 所示。表5 三组试验点取值
Tab.5 Values of Three Groups of Test Points

由表6 跟图8 可知，与最优参数的响应相比，虽然试验点1的声学包质量降低了17.6%，成本降低5.7%，但PBNR 值在（250～10000）Hz 频段均低于最优参数对应的响应，其均值低1.3dB，隔声性能下降较明显；试验点3 对比最优参数的响应，虽然PBNR 均值高出0.6dB，但在（250～10000）Hz 频段内两者的PBNR 值各有所长，降噪性能并无明显优势，需注意试验点3 的声学包质量及成本降低分别增加了16.7%、3.7%；对比基础的声学包方案：PBNR 值为53.2dB，质量11.8kg，成本406.5 元，最优参数的声学包PBNR 值提升了2.0dB，质量降低8.5%，成本降低3.6%，声学包综合性能都得到了改善，说明最优参数的优越性。表6 三组试验点及最优解对应的响应
Tab.6 Response of Three Groups of Test Points and Optimal Solution

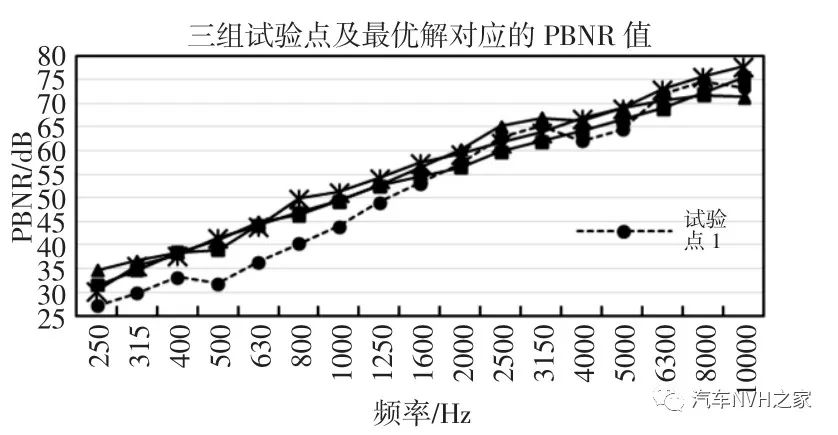
图8 三组试验点及最优解对应的PBNR 值
Fig.8 PBNR of Three Groups of Test Points and Optimal Solution

5 结论

（1）通过搭建SEA 模型并对标试验的PBNR 值，获得中高全程频段的高精度声学包分析模型，可快速获得不同声学包方案的降噪性能及轻量化效果。（2）以影响声学包降噪性能的主要参数为优化变量，结合实际工程，利用最优拉丁超立方采样生成均匀的、随机样本点，以PBNR 均值、声学包质量、成本为优化目标，利用SEA 模型获得各变量对应的响应，在MATLAB 中建立七个自变量与三个响应间的Kriging 近似模型并检验了其预测精度。（3）通过NSGA-Ⅱ算法获得非劣解并通过赋予对应权重确定最优解，与满足要求的前沿解及基础方案对比各响应项说明了最优解的可信性。（4）结合工程实际建立了一套快速有效的整车全频段声学包优化方法，避免了常规的中频段、高频段、单一响应的繁琐优化，为主机厂声学包优化工作提供思路，保证了声学包高性能、轻量化及低成本的最优，缩短了研发周期及成本，对实际工程具有重要指导意义。

作者：李添翼1，2，张永仁3，甘 进4，邱 斌1，2

1.汽车噪声振动和安全技术国家重点实验室

2.中国汽车工程研究院股份有限公司

3.岚图汽车科技公司

4.武汉理工大学