基于多项式的智能车辆换道轨迹规划

本文引自北京工业大学李玮、王晶、段建民《基于多项式的智能车辆换道轨迹规划》

//导读//

以智能车辆换道过程为研究对象，提出一种基于多项式理论的车辆换道轨迹算法。该算法采用矩形对换道车辆及障碍车辆进行包裹，结合换道车辆的边界条件由以时间为参数的多项式计算得到换道轨迹。由该算法生成的换道轨迹符合四段式车道变换模型，并适用于复杂道路环境。新算法将复杂道路环境中期望换道轨迹的求取问题转换为单一参数求取问题，简化了计算，同时考虑了车辆动力学限制对生成轨迹的影响。计算机仿真验证了算法的正确性及有效性，尤其是在复杂路面情况下体现了该换道轨迹规划算法的优势。

无障碍换道轨迹规划

首先考虑换道车辆周围无障碍条件下的轨迹规划问题。在此种状况下不涉及换道车辆与障碍车辆间的碰撞检测问题，可以直接根据换道车辆的边界条件进行路径规划，使车辆在指定时间段t=Δ内达到目标车道，即在初始状态（xin xin xin yin yin yin ）与目标状态（xfin xfinxfin yfin  yfin  yfin ）间寻找一条光滑曲线，如图1所示。

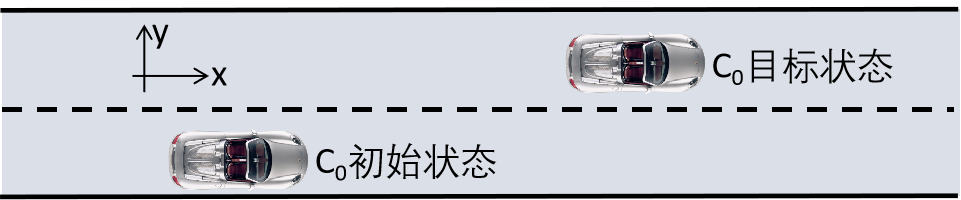
图1 无障碍自由换道

图1中，C0表示换道车辆，在时间段t内完成从初始车道到达目标车道的换道过程，其中xin为换道起始时刻车辆的纵向位置，xfin为换道完成时刻车辆的纵向位置，同理yin与yfin分别为换道起始时刻与完成时刻车辆的横向位置。在x方向与y方向选取5次多项式来构造换道轨迹函数：

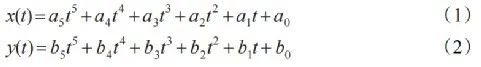
定义时间参数矩阵：

式（3）中tin表示换道初始时刻，tfin表示换道完成时刻。求取换道轨迹即求取式（1）、（2）中的系数矩阵A=[a5a4a3a2a1a0]与B=[b5b4b3b2b1b0]，此时换道轨迹的设计变为寻找满足边界条件的问题，根据边界条件即可求解出式（1）、（2）的系数矩阵。

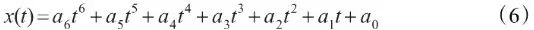
通过求取式（4）、（5）的齐次线性方程组便可求得车辆自由换道轨迹曲线。

存在障碍情况下车辆换道轨迹规划

当换道车辆遇到障碍物时前面得到自由换道轨迹规划算法便失效，原因为它只从换道本身出发，并没有涉及换道过程中可能出现的碰撞问题以及相应的碰撞检测。

考虑换道车辆前方存在一个障碍物情况下的换道路径规划，如图2所示。

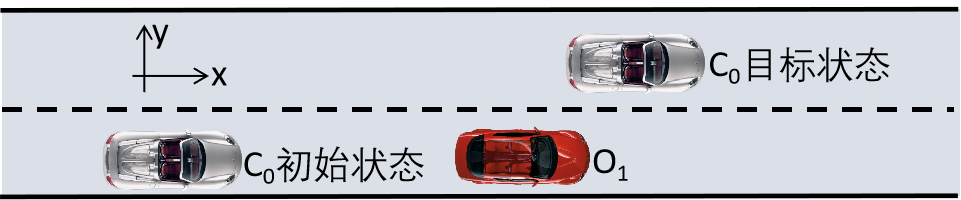
 图2 单障碍物情况下车辆换道

图2描述一超车行为，C0为换道车辆，O1为车道中存在的障碍车辆，C0由初始车道经过时间t变换到目标车道，完成对障碍车辆O1的超越，同时保证在整个过程中与O1不发生碰撞。这种情况下需要增加换道轨迹的约束条件。考虑车辆在实际换道过程中纵向速度的变化范围要比横向速度大的多，其调整的自由度更大，因此本文通过增加X方向的次数来引入约束条件，将X方向换道轨迹函数改写为：

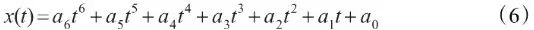
式（6）中，a6为新引入的纵向轨迹参数。重新定义时间参数矩阵：

假设1在换道过程中目标车辆与道路方向夹角为0，即换道过程中车辆呈平动状态。

在实际换道过程中，车辆运行方向与道路方向的夹角不为0，即车辆的偏航角不为0，否则无法完成换道行为，但考虑到该偏航角较小同时换道行为车辆产生的纵向偏航角这一假设是合理的。假设1是实现本文所提出的快速轨迹规划算法的前提条件。

将图2中的换道车辆与障碍车辆进行矩形包裹，见图3

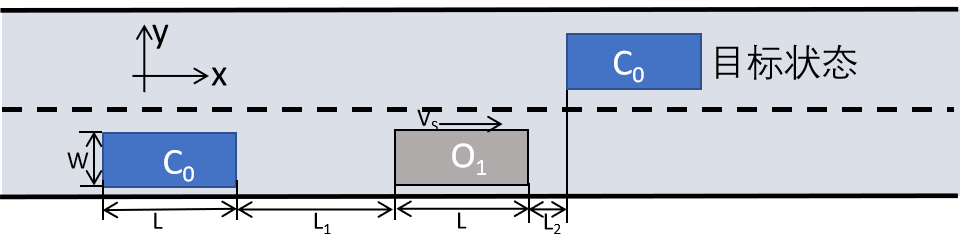
 图3 车辆换道矩形表示

C0车与O1车的长、宽相同，分别为L与W，在换道初始时刻t=tin时C0落后O1距离L1，当换道结束t=tfin时C0超越O1距离，在整个运动过程中O1以速度Vs匀速直线行驶。定义Δ=tfin-tin，即在Δ时间段内换道车辆完成了超车、换道操作。

首先利用式（5）根据C0的初始与目标状态求出系数矩阵B，得到横向换道轨迹函数y（t）；假设在t=tc时刻C0的车头到达O1车位位置，如图4所示，称tc为碰撞时间点。

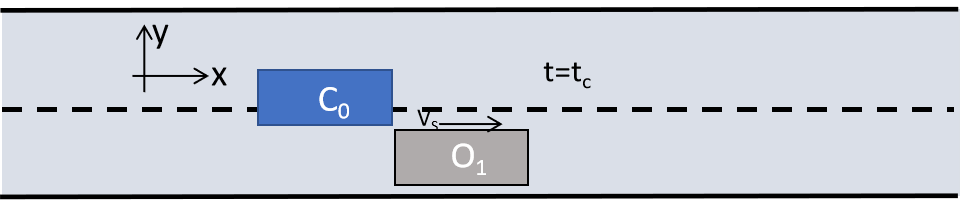
图4 到达碰撞点t=tc时两车位置

可以证明换道轨迹函数y（t）为单调递增函数，因此结合假设1可得到一下结论：

结论1 当y（tc）≥W时，C0与O1不会发生碰撞。

结论1意义为：若辆车在换道过程中不发生碰撞，那么在碰撞时刻t=tc换道车辆C0已经向目标车道方向至少产生一个整车宽度W的位移，等号成立的情况为临界碰撞状态。在图3所示换道过程中，对C0车的下边缘与前边缘和O1车的后边缘与上边缘做碰撞检测，由此可得到X方向参数矩阵A中a6的参数矩族。得到了a6值外加边界条件便可以求得X方向参数矩阵，这样就将寻求换道轨迹问题转化为寻求一个合适的a6值的问题。

给定一边界条件与车辆、道路参数：[xin xin xin yin yin yin]=[0 10 0 0 0 0]，[xfin xfin xfin yfin yfin yfin]= [1 10 17 0 3.5 0 0] 车道宽度为3.5m，L=4.5m、W=1.75m。

图5为进行碰撞检测时a6变化曲线。当a6=-0.04，C0车与O1车大约在2s时两车发生碰撞。在该例中tc=4，对应的a6=-0.015，此时的a6值为临界碰撞值，也就是结论1中等号成立的状况，理论上当a6值大于该临界值时图3中的两车不会发生碰撞，但实际情况a6值得选取与车辆得动力学限制有关，在下一章将专门对此讨论。

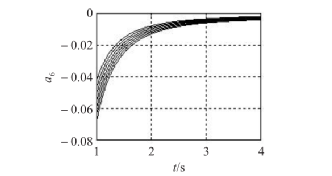
图5 a6值变化曲线

车辆动力学限制

采用以上提出的轨迹规划算法可以快速地获得换道轨迹，但此时得到的换道轨迹并没有考虑其受车辆动力学特性的约束，车辆在实际运动过程中产生的纵向及横向加速度受到发动机、轮胎、地面摩擦力等多方面限制，同时为了保证换道过程中乘坐的舒适性也要对换到过程产生的最大纵向及侧向加速度进行约束，取换道产生的纵向及横向加速度（m/s2）满足：

-2.5＜x＜2.5      （8）

-2＜y＜2      （9）

式（8）、（9）定义了换道轨迹的舒适性范围，即生成的路径轨迹性能参数不应超出此范围。如果计算得到的路径轨迹性能指标超出了该范围，需要调整换道车辆的边界条件以及换道时间Δ，重新进行路径规划以使其满足乘坐舒适性要求。一般来说Y方向加速度限制容易得到满足，由于Y方向系数矩阵B的计算与X方向系数矩阵A相独立，因此若计算得到的换道轨迹不满足式（9），那么仅需要调整参数Δ直到满足最大横向加速度限制即可。前面本文已将复杂路况下的换道轨迹规划问题转化为寻求合适的X方向系数矩阵参数a6的问题，因此这里提到的车辆动力学限制问题同样归结于a6值的选取问题。

实验仿真

以一复杂交通状况下的车辆换道行为进行仿真实验，来验证本文提出的轨迹规划算法。

如图6所示，车道中存在障碍车辆O1与O2，间隙的穿越，即图6中虚线所示，为此需要规划一条换道轨迹保证在换道过程中C0与O1、O2车辆不发生碰撞，同时满足乘坐舒适性要求。其中O1与O2两车始终保持匀速直线运动，速度为Vs=10m/s,三车外形尺寸相同，长宽分别为L=4.5m与W=1.75m，车道宽度为3.5m，S=10m，C0车的初始与目标状态分别为xin xin xin yin yin yin]=[0 10 0 0 0 0]，[xfin xfin xfin yfin yfin yfin]= [1 10 16 0 3.5 0]，换道时间Δ=8s。利用本文提出的算法求取a6值范围。

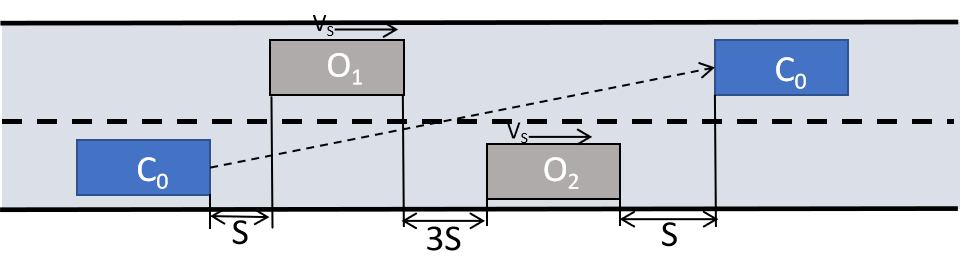
图6 一般车辆换道问题

如图7可知，当-0.0031738≤a6≤0.00061035时，即图7中灰色区域所表示的范围，得到的换道轨迹能够保证换道过程中C0与O1、O2两车不发生碰撞，其中t=4s为碰撞点，即tc=4。接下来对得到a6值进行乘坐舒适性检测。

图8为换道轨迹产生的最大纵向加速度a6值变化的曲线，由图可知在a6=-0.0002时，换道轨迹产生的最大纵向加速度最小，为1.22m/s2，满足车辆动力学及乘坐舒适性约束。选取a6=-0.0002，根据边界条件最终求得换道轨迹为：

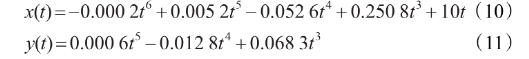
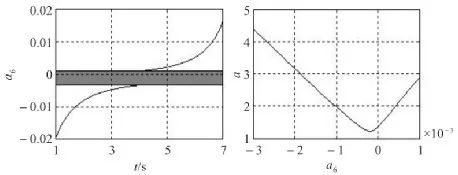
      图7 a6取值范围      图8 车辆最大纵向加速度变化曲线

如图9所示，由本文提出的算法得到的换道轨迹具有较好的性能指标，X方向速度及及速度变化平稳，Y方向加速度变化满足四段式车道变换模型，与车辆实际换道过程完全相符。在结论1的保证下，该算法在实际应用过程中只需分别计算出换道车辆与不同障碍车辆在碰撞点t=tc处的a6值便可得到其取值范围。如图6中的换道问题，a6的下边界为C0的右前角点与O1的左后角点的临界碰撞时的值，a6的上界为C0的左后角点与O2的右前角点的临界碰撞时的值；在确定a6取值范围后利用车辆动力学及乘坐舒适性约束找出乘坐舒适性最优的a6值从而得到换道轨迹。由于该算法建立在假设1之上，因此在车辆参数建模过程中适当加大长宽值能够提高换到轨迹的安全系数。

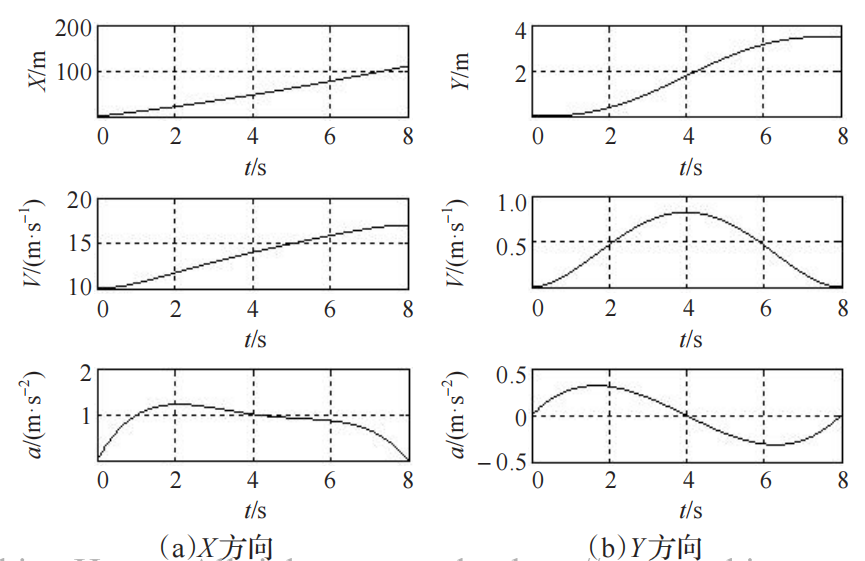
图9  车辆换道轨迹的位置、速度、加速度曲线

结论

提出一种新的基于多项式的车辆换道轨迹快速规划算法，该算法对换道车辆及障碍车辆采用矩形包裹并进行碰撞检测，将寻求一条合适的换道轨迹问题转化为X方向多项式参数a6的求取问题，最后通过引入车辆动力学及乘坐舒适性从而求出换道轨迹。该算法的特点为：计算简便，通过引入车辆障碍物碰撞检测使该算法适用于复杂交通状况下的换道轨迹规划，由于在结构化公路上的绝大多数车辆换道行为都可以分解为第2章及第3章提到的换道动作，因此该算法的适用范围广；并且由于引入车辆动力学及乘坐舒适性的约束使得车辆换道行为进行了实验仿真，仿真结果验证了算法的正确性及有效性，该算法具有一定的实际应用价值。