外部噪声源对内部气动噪声影响的研究

摘要

为了研究汽车气动噪声传递到客舱内部的机理，利用风洞实验测量和基于晶格玻尔兹曼方法(LBM)的计算流体动力学(CFD)方法研究了汽车气动噪声的流动结构和声场。在本研究中，重点研究了前侧窗玻璃的传输噪声。侧窗玻璃上的压力波动既包括流场对流引起的水动压力波动，也包括噪声源传播的声压波动。但考虑到实验传输损失，发现在高频范围内声压波动对侧窗玻璃的影响较大。另一方面，在低频范围内，水动力压力波动占主导地位，而在高波动水平时，水动力压力波动对传输噪声的影响不大。

1.介绍

高速巡航过程中舒适性的提高逐渐成为乘用车的重要卖点。由于气动噪声的大小随着车辆运动速度的加快而迅速增加，因此降低车辆周围湍流的气动噪声变得非常重要。最近，电动汽车引起了公众的广泛关注，并迅速普及开来。电动汽车由电池和电机驱动，因此其动力系统的噪音比传统发动机汽车小得多。由此可见，电动汽车周围流动产生的气动内部噪声更加显著。为了降低气动噪声，在汽车研制阶段需要进行许多改进。

要降低汽车客舱的气动噪声，需要了解以下机理:噪声的产生机理和从车身外部到客舱的传递机理。汽车内部噪声通过车身表面传播，存在水动压力波动和声波。这些复杂的区域被称为声近场。没有近场流场和声场之间的关系，很难估计内部气动噪声。为了分离水动压力和声波成分，提出了波数-频率谱。该方法利用压力场的时空相关函数分离这些分量。波数-频率分析和统计能量分析(SEA)方法相结合的室内噪声估计已有报道。分析流场声源与车体表面压力波动之间的关系，为降低车体内部噪声提供理论依据。

本文研究了气动噪声通过侧窗玻璃传输的问题。通过风洞试验和数值分析，得到了侧窗玻璃的压力脉动分布。通过实验测量了靠近侧窗玻璃的车内噪声分布。通过对这些侧窗玻璃内外分布的比较，探讨了噪声传播的机理。

2.数值方法

2.1 数值方案

采用CFD程序PowerFLOW计算非定常流动现象。代码基于LBM。与传统的基于求解Navier-Stokes方程的方法不同，LBM从“介观”级动力学方程出发，基于粒子分布函数的离散Boltzmann方程，通过演化基本粒子分布得到正确的宏观流体动力学。

晶格玻尔兹曼方程的形式如下:

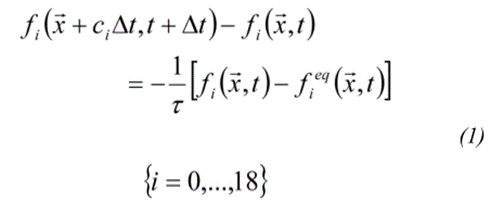
式中，fi:根据离散速度向量的有限集合，沿第i个方向运动的粒子分布函数，

空间增量，Δt:时间增量，τ:单个松弛时间参数，

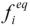
是局部平衡分布函数，它取决于局部水动力性质。为了简单且不失通用性，本文使用了三维速度(D3Q19)模型。等式(1)右侧的碰撞项采用了最简单也是最流行的Bhatnagar-Gross-Krook (BGK)形式。基本的水动力量是通过力矩求和得到的;即:

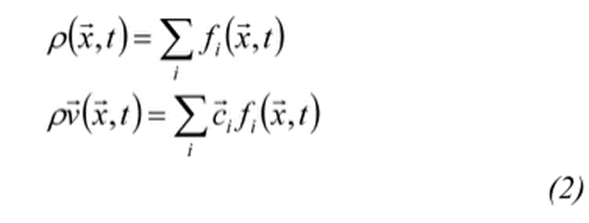
2.2 计算条件

我们选择了全尺寸、详细形状的小型电动汽车作为测试车辆(图1)。表面元素的数量为750万。空间最小网格尺寸为1mm。为了解决后视镜尾流结构和A柱周围分离流的问题，详细确定了A柱、雨刷和后视镜周围的网格分布。由于这些流动分离产生的噪声源较多，因此对空气声学影响较大。这辆车的雨刷片不对称，无法进行对称模拟。因此，计算网格的总数约为5900万体素。

为了避免声波在计算域边界处的反射，网格尺寸逐渐增大到边界处，以使声波消散。边界处网格尺寸为1m。时间步长6.42×10−6秒，可解决高频气动噪声。压力数据每12步采集一次(采样频率-13000 Hz)。采用0.05秒的时间序列数据进行快速傅立叶变换(FFT)分析。因此，在计算条件中不考虑200-6500Hz的频率范围。车辆周围的流动速度设置为每小时100公里，没有侧风。

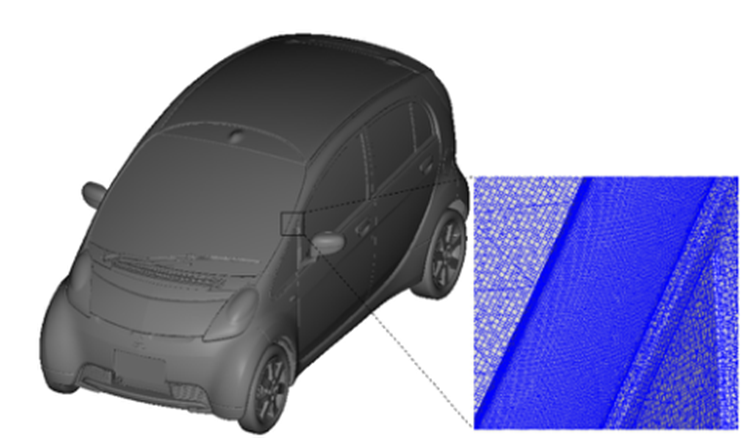
图1 测试车辆和表面网格

2.3 实验方法

在三菱汽车公司全尺寸车身风洞中对试验车辆的流场和气动噪声进行了测量。试验车辆的形状与CFD模型相同。为了消除由于客舱内外压差造成的泄漏噪声的影响，车辆表面的所有缝隙都是密封的。在这项研究中，室内噪声通过前侧窗户玻璃传输的重点。用表面传声器(B&K 4949)测量前侧窗玻璃上的压力波动。这款麦克风的膜片为10mm，厚度为2mm。它的灵敏度为11.2mV/Pa，动态范围为30-140dB。为了减小麦克风对流场的影响，采用锥度盖对麦克风周围的间隙进行平滑处理(图2)。通过与闪光灯安装压力波动数据的对比，验证了麦克风及其盖的凹凸效应。汽车客舱内部噪声的声场是非常复杂的，因为受到来自车身各部分的传输噪声、声音在客舱内的散射、反射和吸收等多种影响。为了提取通过前侧车窗玻璃传输噪声的影响，用1/2英寸电容麦克风(B&K 4190)测量靠近前侧车窗玻璃的内部噪声。在除目标玻璃区域外的玻璃上放置吸声材料，并将玻璃与麦克风之间的距离设置为1mm，以减少其他声音来源得影响。测量了外表面压力分布和内部噪声。测点为前侧窗玻璃上的45个点(图3)。通过分布图像对两种结果进行了比较。

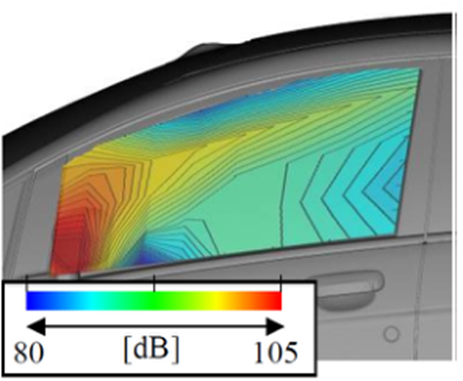
图2 表面麦克风

图3 测量前侧玻璃上的45点

3.结果和讨论

3.1 数值结果

3.1.1 噪声源分布

侧窗玻璃上的表面压力波动既包含水动压力波动，也包含所谓声波的声波成分。空气对流引起的水动压力波动与声波传播的声波波动有很大的区别。这些水动力和声压波动是由气动噪声源的非定常运动引起的。

Lighthill方程(3)是流场与声场相结合的方程:

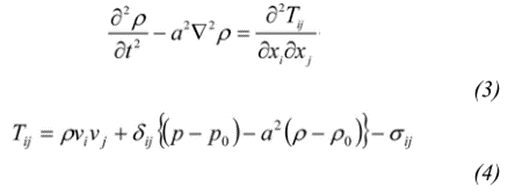
该方程完全由可压缩Navier-Stokes方程、连续方程和声速定义推导而来，没有任何假设。本文将式(3)的右侧作为气动噪声源。Lighthill的应力张量由三个项构成。第一项是雷诺应力项，第二项是与压缩有关的项，第三项是粘性应力张量。在低马赫数和高雷诺数的流动中，如绕车身流动，压缩和粘度的影响可以忽略不计。因此，式(4)大致写成如下形式:

在车身周围流场中，通过数值计算得到了第二项和第三项对Lighthill应力张量的贡献。它们的阶分别约为第一项的10-4和10-2。因此，Lighthill的噪声源被定义为二阶微分:

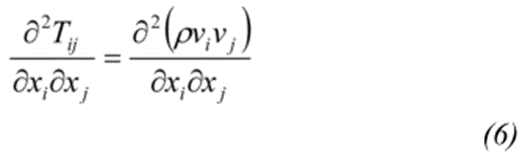
由式(6)可知，Lighthill的噪声源由空间速度梯度产生。平行于地面的截面平面上的速度和Lighthill的噪声源如图4所示。截面平面放置在后视镜的中间。在A柱和后视镜尾迹周围形成速度梯度较大的剪切层。Lighthill的噪声源产生于观察到剪切层的同一位置。这意味着气动噪声主要产生于剪切层，并向空间传播。

计算得到的Lighthill噪声源分布在侧窗玻璃上(图5(a))。这意味着水动压力波动在侧窗玻璃上占主导地位。众所周知，噪声源产生的声波强度随距离的平方而减小。而水动压力波动使其强度随距离的四次方下降。这意味着，随着离噪声源的距离越远，水动压力波动迅速减小。远场压力波动水平与近场压力波动水平ξ值之比表示为:

其中f:声音频率[Hz]，r:到声源的距离[m]，a:声速[m/s]。

在声近场，水动压力波动占主导地位。另一方面，远场只有声波存在。近场和远场的边界一般定义在

处，波长λ。由于声波波长较长，声波近场在低频范围较宽。另一方面，在高频范围内，侧窗玻璃的表面由于波长短得多，可视为一个声远场。例如，波长在500Hz时约为680mm，在5000Hz时约为68mm。因此，到声近场和声远场边界r的距离分别为108mm和10.8mm。

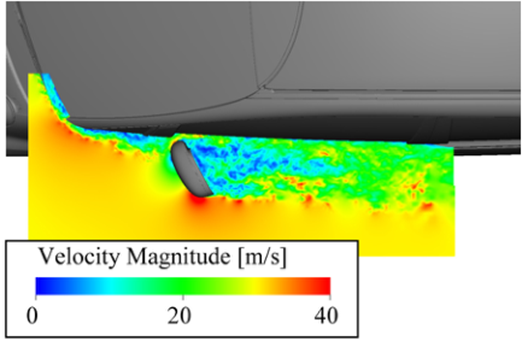
a 速度大小

b Lighthill噪声源

图4 速度分布与Lighthill噪声源的比较

a Lighthill的前侧玻璃周围的噪声源

b 侧视镜尾迹中的Lighthill的噪声源

图5 Lighthill噪声源的等值面

3.1.2 压力波动分布

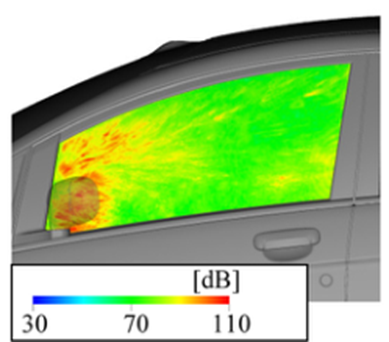
侧窗玻璃上的压力波动由水动压力波动和声波组成，因为Lighthill的噪声源项(图5)包含了这两种波动。水动压力波动的幅度大于声波波动的幅度。图6为侧窗玻璃上的压力波动分布。根据数值模拟结果进行FFT分析分布，取50%重叠平均，对时间数据块施加汉宁窗口，参考压力为2×10−5 Pa。在250-750Hz(低频)和4000-5000Hz(高频)的不同频率范围内，后视镜附近的压力波动都很大。这些频率范围被选为典型的低频和高频范围。其他频率范围也显示出同样的趋势。

压力波动较大的区域是由A柱涡和后视镜与反射镜基座之间的高速流动造成的(图7)。这些高水平的压力波动是由车辆周围的流动对流产生的。一般情况下，声波波动级的数量级比水动压力波动小1/100。因此，在数值或实验结果的FFT数据中很难发现声波的影响。

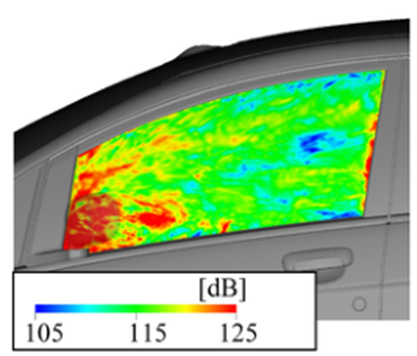
a 250Hz— 750Hz

b 4000Hz — 5000Hz

图6 用CFD计算侧窗玻璃的压力波动(dB图)

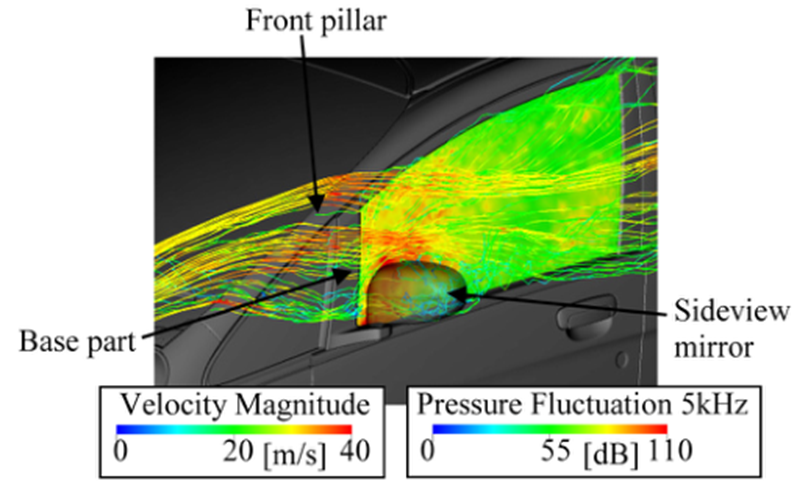
图7 流线周围的侧视镜和前支柱

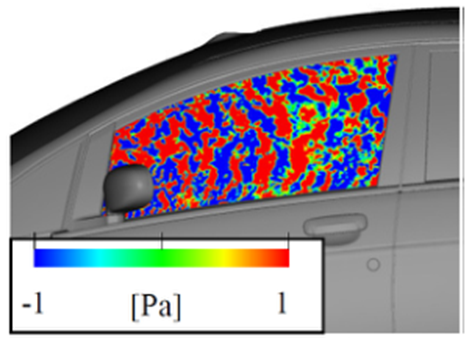
3.1.3 瞬时压力波动

为了使声波可视化，瞬时压力波动如图8所示。从时间序列压力波动得到的时间平均dB值不能观察到声波等小波动。计算瞬时压力波动的方法是:对时间序列的压力历史进行FFT分析，然后对其频域数据进行聚焦频率范围的带通滤波。最后，利用傅里叶反变换方法得到时域压力波动.由于水动压力波动具有不同的波长，因此可以通过可视化结果将两者区分开来。在低频范围内(图8(a))，整个侧窗玻璃的水动压力波动较大，波数大于声波。另一方面，在高频范围内(图8(b))，既可以观察到水动压力波动，也可以观察到波数小于水动波动的声波。在观察到水动压力波动的区域也应该存在声波，但声波的波动水平小，所以看不见。然后观察到图8的水动压力大波动区与图6的压力大波动区相对应。

低频声音具有大波长，侧窗玻璃呈声近场。因为Lighthill的噪声源产生的水动压力波动不会在车身表面消失。另一方面，高频水动压力波动可能因其波长短而有足够的耗散长度而减小。在这种消散的区域，声波就出现了。这意味着侧窗玻璃的表面不仅要作为近场处理，还要部分地作为远场处理。在低频(250-750Hz)范围内瞬时压力波动分布的RMS值表明，侧窗玻璃受到水动压力波动的激励，且整个侧窗玻璃的幅值较大。在高频(4000-5000Hz)范围内，声波激发除后视镜周围外的侧窗。Lighthill的噪声源存在于侧窗玻璃附近，引起了侧窗玻璃上的水动压力波动。后视镜尾迹产生的水动压力波动在传播过程中减少。然而，声波似乎能够到达侧窗玻璃。

a 250Hz—750Hz

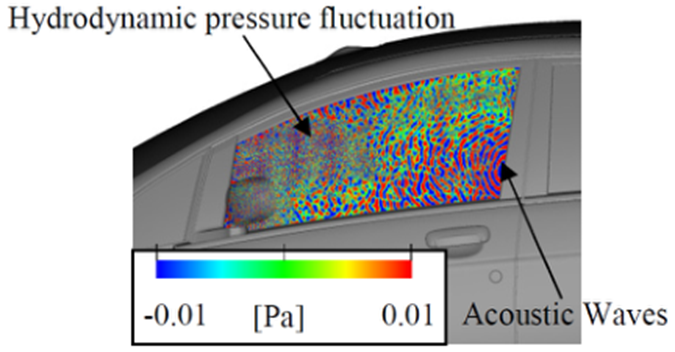
b 4000Hz — 5000Hz

图8 基于CFD的瞬时压力波动

3.2 实验结果

3.2.1 压力波动分布

图9为侧窗玻璃表面压力波动水平分布。它是由表面麦克风测量的。研究发现，在500Hz和5000Hz条件下，侧窗玻璃前至中间区域的波动水平较高。这些分布规律与图6所示的数值结果在性质上是一致的。

a 500Hz

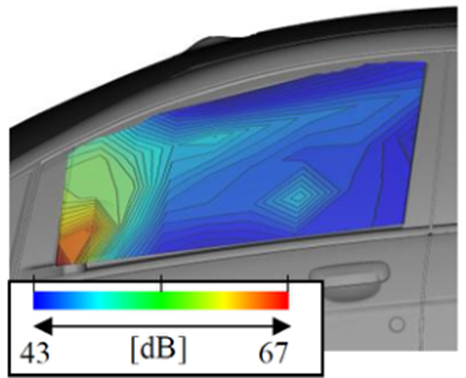
b 5000Hz

图9 侧窗玻璃的压力波动(dB图)实验研究

3.2.2 侧窗附近空间声压级分布

靠近侧窗玻璃的内部噪声分布由1/2英寸电容传声器测量。声压级分布如图10所示。500Hz的声压级在靠近后视镜的区域最大。大声压级区域对应于侧窗玻璃外部的大压力波动区域。在500Hz等低频范围内，水动压力波动的贡献大于声波的贡献。因此，内部噪声(图10(a))和外部压力波动(图9(a))的分布规律是一致的。

另一方面，在5000Hz等高频范围内，水动压力波动和声波都会激发侧窗玻璃。这意味着侧窗玻璃的激发非常复杂。后视镜周围的侧窗玻璃在5000Hz处外部压力波动最大。然而，就车内噪声而言，后视镜周围区域的噪声水平并不是最大的。如图8(b)所示，在某些区域，较大的内部噪声区域对应着声波存在的区域。虽然水动压力波动的水平远大于声波波动，但水动压力波动对内部噪声的影响可能小于声波波动。在低频范围内，由于水动压力波动水平远大于高频范围，因此对内部噪声的影响较大。另一方面，声波在高频范围内对室内噪声有一定的影响。这意味着水动压力波动和声波对内部噪声的传输是完全不同的。

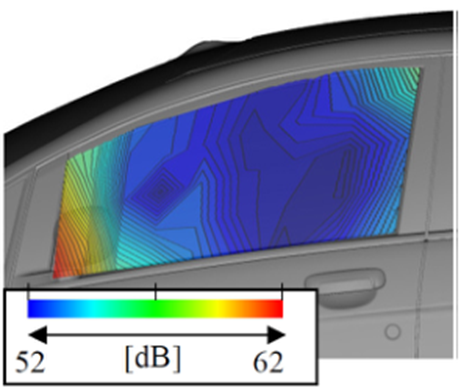
a 500Hz

b 5000Hz

图10 室内声压级的实验分布

3.2.3 表面压力波动与室内噪声反计算声压级的比较

玻璃外侧表面有水动压力波动和声波的共同作用。然而，由于很难区分它们对内部噪声的贡献，要估计这些贡献，外部声压级是从内部噪声分布假设的。该计算是基于声传输损耗理论进行的。假定声波的入射是随机入射，声波通过侧玻璃的传播满足质量定律。

由入射声的声强和透射声的声强，透射损失TL [dB]表示为:

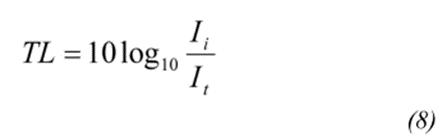
假设入射和传播的声音都是平面波，计算声强。

由随机入射质量定律确定了传输损耗TL。TL用正入射质量定律TL0表示。TL和TL0表示为:

从这些方程中得到的内部声压级可以计算出每个频率的入射声压级。图11为计算的入射声压级与图9所示的实际外部压力波动级dB值之差。

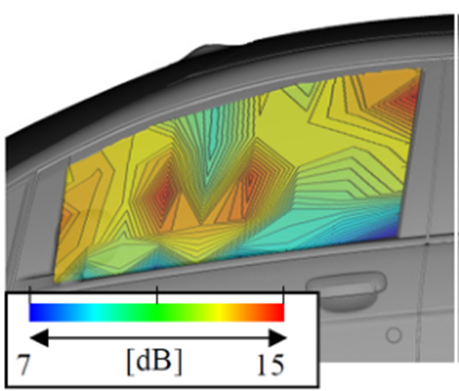
表面传声器测得的压力波动水平远远大于500Hz时估计的入射声压水平。这种趋势在整个侧窗区域都有体现。认为整个侧窗区域存在低频水动压力波动。压力波动特别大的区域对应图9中压力波动特别大的区域。在5000Hz的差异不是那么大，除了在后视镜周围。这意味着侧窗玻璃被认为只由高频声波激发。在高频范围内，外部压力波动分布模式与内部气动噪声分布模式定性不匹配。从FFT分析的表面压力波动水平很难估计内部噪声。

图8(b)所示，在仅声波激发侧窗玻璃的区域，由外表面压力波动与内声压级之差计算出的传输损失与由随机入射定义的质量定律传输损失进行比较。准确地说，由于外界压力波动也包含了水动力分量，因此估计的传输损失与定义不同。然而，如图12所示，在4000Hz附近，估计的传输损失与随机入射质量定律几乎很好地一致。这意味着在高频范围内的表面压力波动大部分是声学成分。

基于以上考虑，明确了利用CFD结果定量估算内部气动噪声时，压力波动应分为水动压力波动和声波分量。此外，还需要水动压波动和声波在每个频率下的传输损失。如前所述，在高频范围内的传输损耗可以由随机入射质量定律得到。但在低频范围内，需从近声场时空相关谱的传输机理考虑。

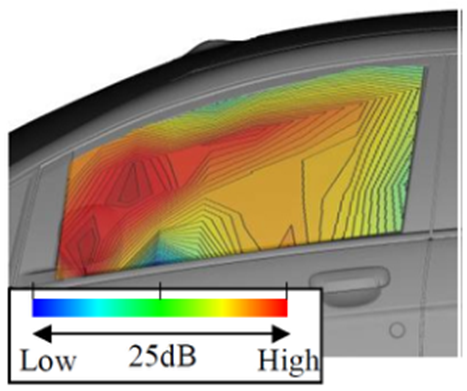
a 500Hz

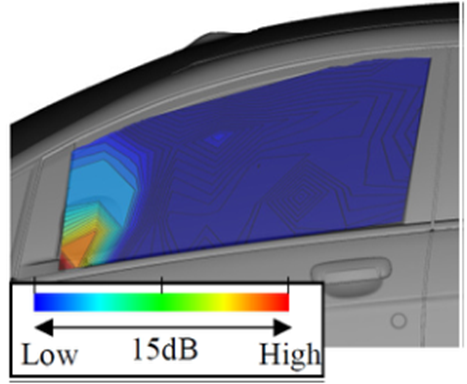
b 5000Hz

图11 由传输损失承担的表面压力波动级与外部声压级之差

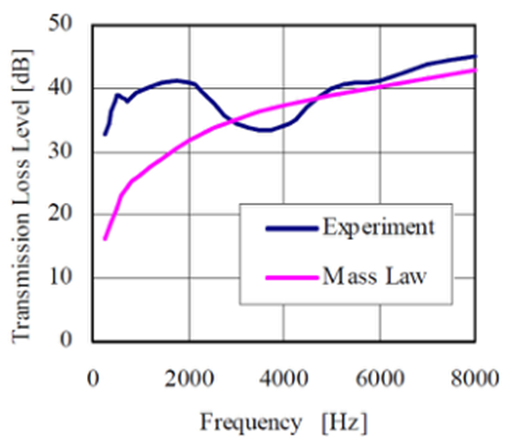
图12  比较了实验传输损耗和随机入射质量定律的结果

4.结论

通过对汽车侧窗玻璃气动噪声的数值研究和实验研究，得到以下结论:

• 侧窗玻璃的瞬时压力波动表明，水动压力波动在低频范围内分布在整个侧窗玻璃上。另一方面，声波主要在压力波动水平较低的区域对侧窗玻璃进行激励。

• 在低频范围内，侧窗玻璃外部压力波动与内部噪声分布在质量上是一致的。在高频范围内，这些分布表现出不同的规律。

• 利用声传输损失理论方程，从内部噪声水平估计外部压力波动。将估算的压力波动与实际压力波动进行比较。结果表明，水动压力波动和声波波动对室内噪声的影响是不同的。

• 在低频范围内，内部噪声主要受机体表面水动压力波动的影响。另一方面，在高频范围内，应考虑声波激励来估计内部噪声水平。

文章来源：Hamamoto N, Okutsu Y, Yanagimoto K., “Investigation for the Effect of the External Noise Sources onto the Interior Aerodynamic Noise,” SAE Technical Paper 2013-01-1257, 2013, doi:10.4271/2013-01-1257.