广告
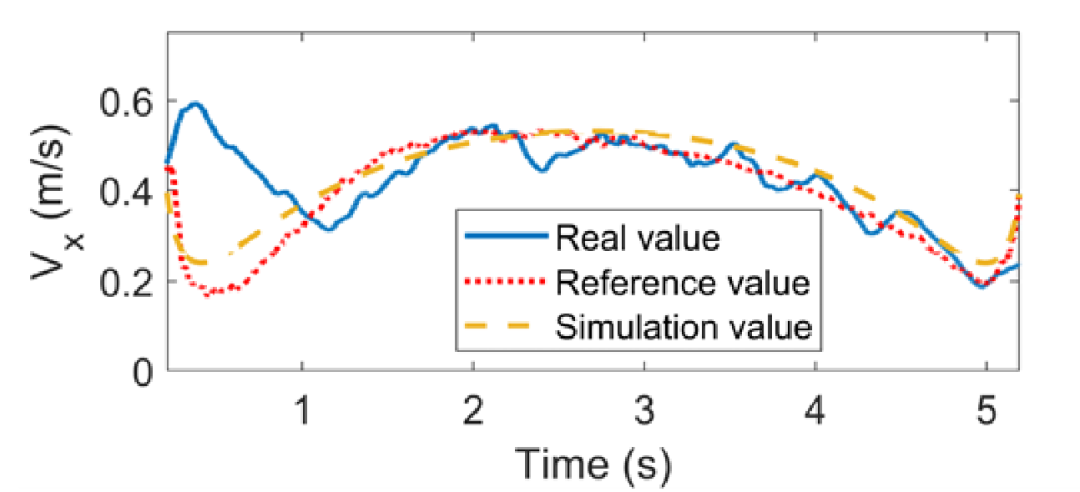
基于正弦曲线的自动车辆横向运动规划方法
（2）在保持侧向位移和零转向角不变的情况下，利用v1和v2的正弦输入将车辆转向目标余弦值；
（3）由于系统(4)现在处于奇异位置，我们用u1恒速控制到达目标位置。为了处理这一步，全局参考框架应该与目标配置对齐。尽管上述过程看似合理，但实际上仍然很难应用。首先，在步骤（1)中，我们要仔细选择v1输入，使y趋近于它的目标值，并确保它返回零，因为在步骤（2）之后v1的值应该收敛于零。假设u1为正，方向θ也应归零。实现第一步的困难与整个问题是一样的。换句话说，提议的过程很难开始。另一个问题是，对于任何正弦输入，如asin(t)+bcos(t)，它的值越过零点，v1的负值导致负车速u1，这对我们的目的来说是不可接受的。为了克服上述问题，我们建议将前两步合并为一步过程，并使用带偏差的正弦曲线，表示如下:
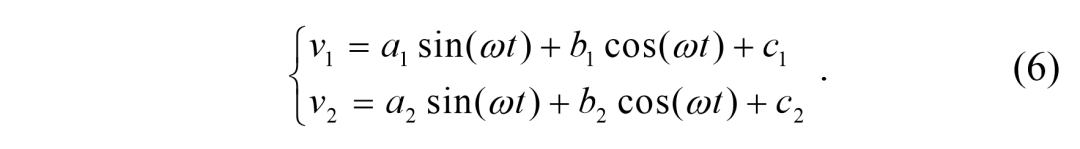
这里的频率ω=2π/τ, τ表示计划运动的周期。a1，b1，c1， a2,，b2和c2是待确定的设计参数。在此过程中，控制输入v1和v2均为
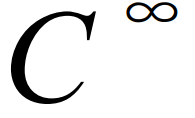
正弦函数，为实际应用带来了方便。对(6)积分一段时间，根据状态y和φ的目标值，可以确定偏差c1和c2。根据输入的扩展形式，周期过后输入v1的值保持不变。这里我们考虑两种情况。如果一步过程改变了车辆方向，那么车辆的初始或最终速度应该为零，以满足v1(0)=v1(τ)=0的关系，因为我们总是倾向于根据初始或目标配置来选择全局帧。如果一步过程不改变车辆方向，则始终满足上述关系。由于我们不应该要求车辆在计划的时间前后停下，一步法更适用于横向运动的情况(如变道)。接下来，我们主要关注横向运动情况，选择与初始构型一致的全局参照系。显然，v1(0)=0表示b1+c1=0。除非我们选择a1=0，那么v1剖面将穿过零点。接下来，我们建立(6)中的六个参数之间的关系，以确保 α 值在一步过程之后不会改变。根据系统(4)和控制规则(6) ，对前轮转向角度进行了如下整合，
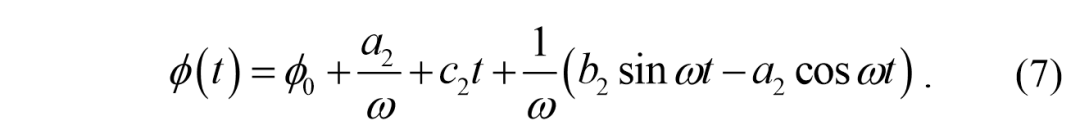
对于系统(4)的结构，我们把状态方程α看作一个类似的链式形式，因为当转向角接近零时，函数tan (φ)≈ φ。扩展功能
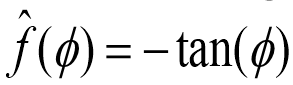
用它的傅里叶级数，我们有，
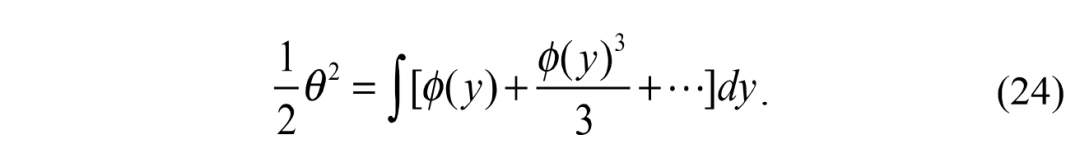
通过对 α 的微分方程积分一个周期，最终的值可以得到如下，
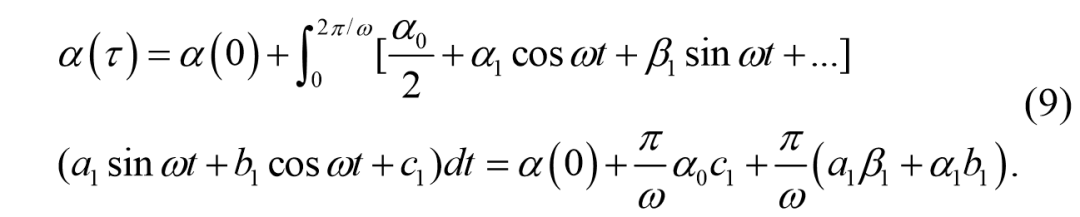
由于正弦曲线的良好特性，只有几个项有助于α的变化。对于这些项的解析表达式，根据(7)近似得到以下傅里叶系数，
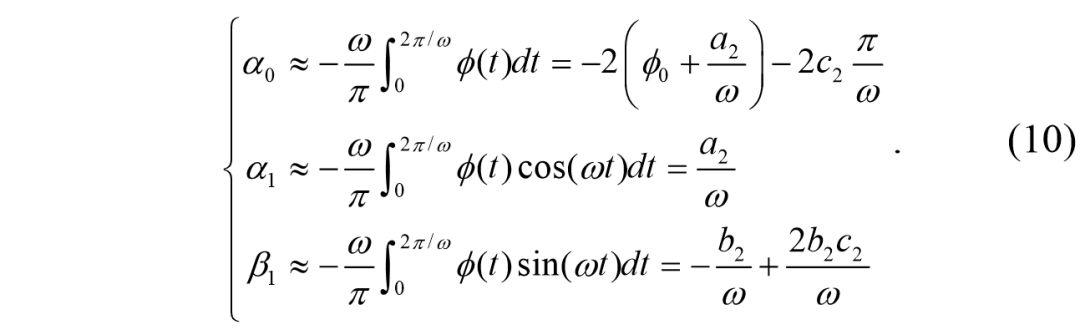
将这些值代入方程(9)，我们得到，
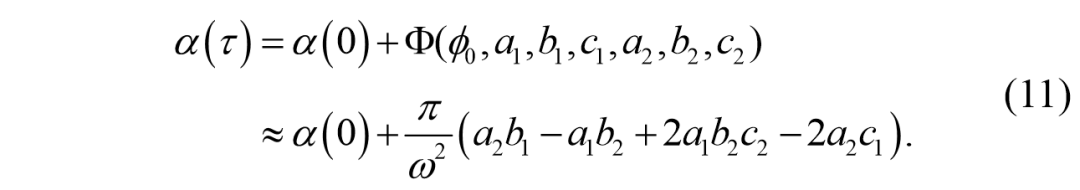
这里我们得到了α的转移函数的一个线性估计。此外，如前所述，在建议的一步过程之后，车辆的方向不应该改变，也就是说，
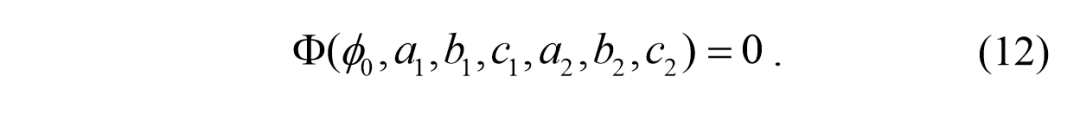
将
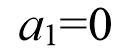
代入(12) ，得到
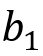
。假设平面运动前后的转向角
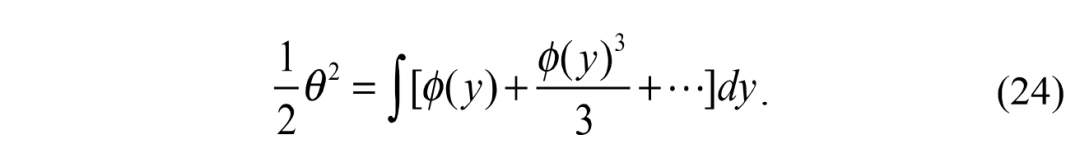
为零也是合理的，导致
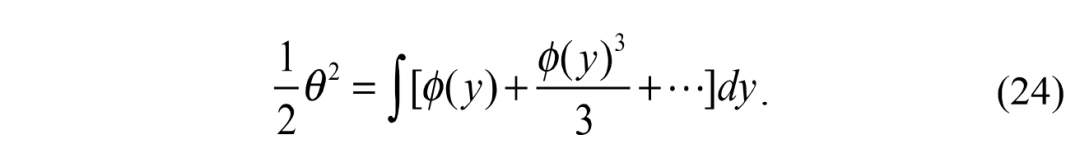
。遵循这些原则，系统(3)的开环控制规则可以概括为：
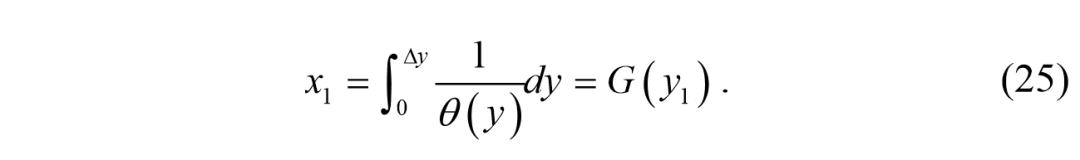
其中
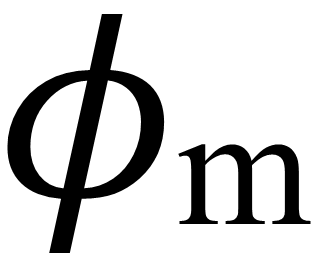
是一个给定值不大于物理极限的最大转向角。根据给定的控制规则，可以精确地实现所需的横向运动，并且通过积分(3)中的第一个方程来确定纵向位移
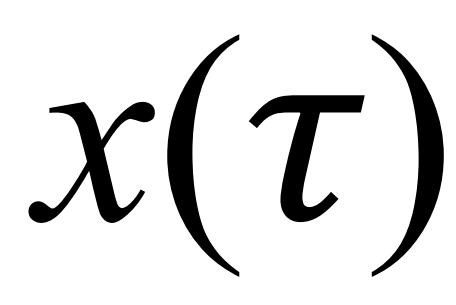
。如果目标的纵向位置大于
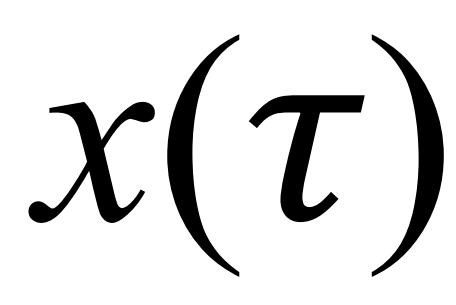
，我们可以用一条直线路径来补偿这一误差，这条直线路径可以在计划的横向运动之前或之后灵活安排。
然而，一个约束，我们应该进一步考虑来自初始车速
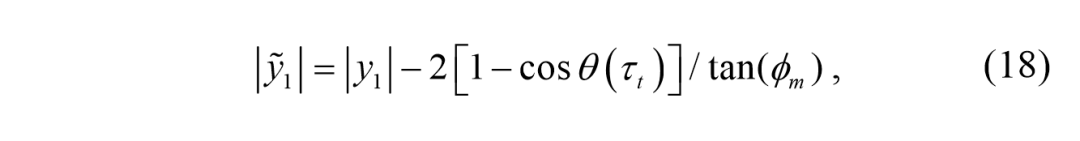
。根据(13)中的
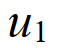
控制规则，当t→0时，分子和分母都收敛到零。我们根据洛必达法则表示初始速度，
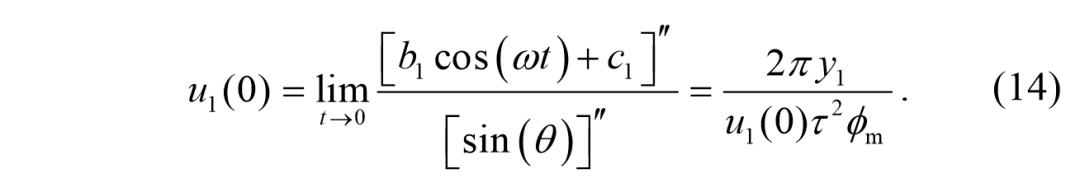
该方程建立了给定
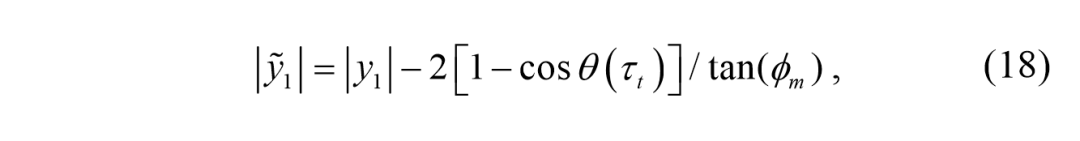
的周期τ与最大转向角
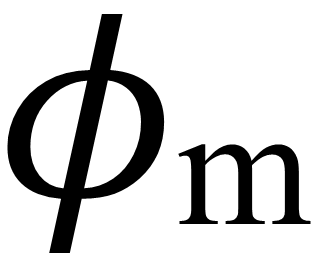
之间的关系。这意味着不可能同时调整路径模式(用
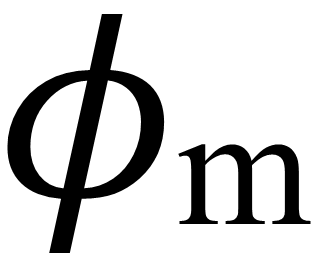
)和周期时间。此外，由于
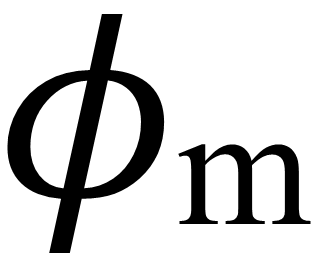
是上界的，因此τ的周期不能任意小。在紧急情况下，如规避转向，τ的限制可能是不可取的。为了摆脱约束(14) ，我们建议引入一对对称的过渡期，以帮助实现可调速度分布。进入/离开过渡的周期表示为
。在入口过渡的开始，我们试图增加转向角度尽可能快到
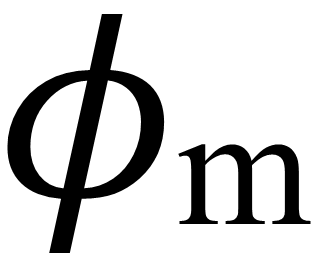
产生初始横向速度
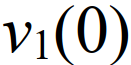
。类似地，当人类驾驶员在回避转向和回收情况下做出反应时，在离开过渡结束时，我们可以很快地将转向角度恢复到零。不考虑开始/结束脉冲，(13)中的控制规则可以修改为，
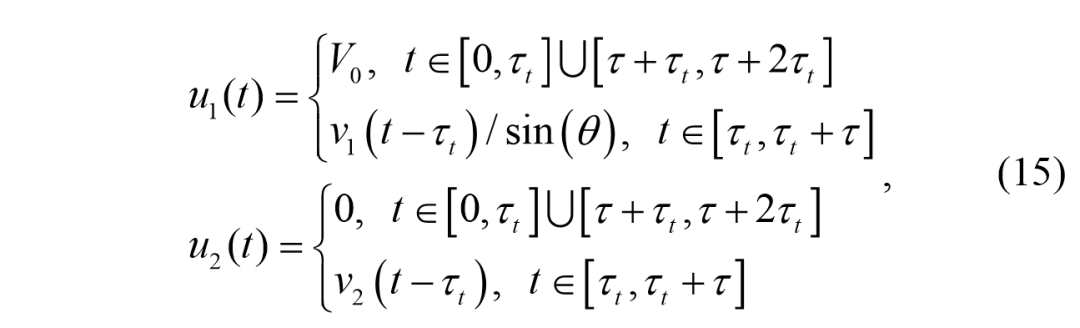
其中
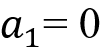
是初始车速。然而，现在(6)中参数的确定是不同的。原点条件
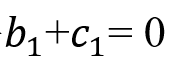
和
转化为，
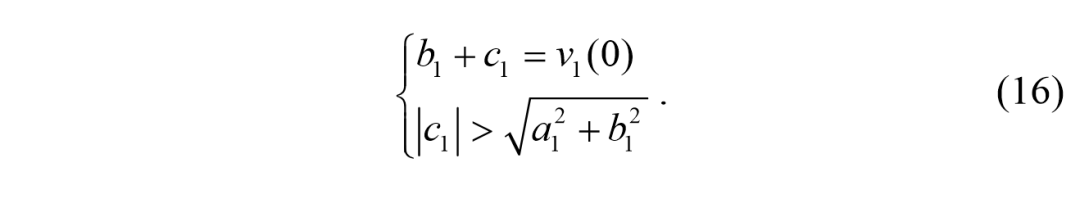
为了简单起见，我们仍然选择
广告
广告
编辑推荐
最新资讯
-
直播｜中汽中心 工程院：汽车智驾技术主题
2024-11-24 11:43
-
直播｜中汽中心 工程院：无人驾驶车路云一
2024-11-24 11:42
-
直播｜中汽中心 工程院：基于无人驾驶矿卡
2024-11-24 11:41
-
直播｜中汽中心 工程院：超声波雷达测试系
2024-11-24 11:40
-
直播｜中汽中心 工程院：基于车路云图的无
2024-11-24 11:40
广告
广告
