基于正弦曲线的自动车辆横向运动规划方法
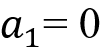
来保持
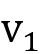
远离0,通过解(12)得到
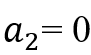
。由于状态
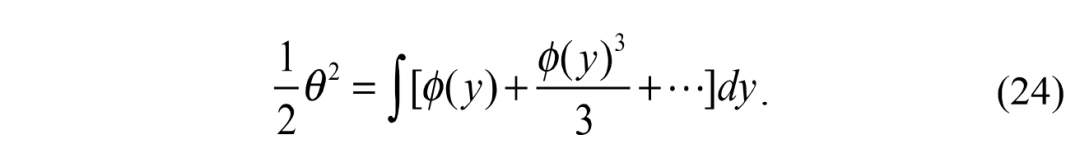
从
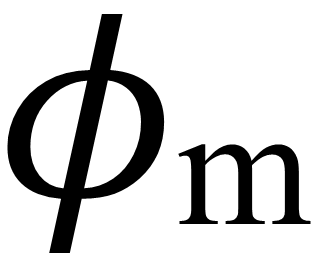
变为-
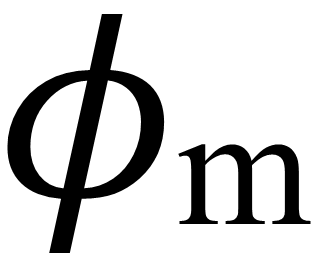
(对于
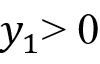
),我们可以得到
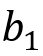
和
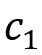
值。对于一步过程和跃迁路径的对称性和连续性,我们假设它们之间的关系为
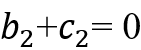
。在这些条件下,横向运动规划器的一个例子如图2所示。结果表明,一步过程前后的路径方向保持平行,两个过渡期的形状是对称的。
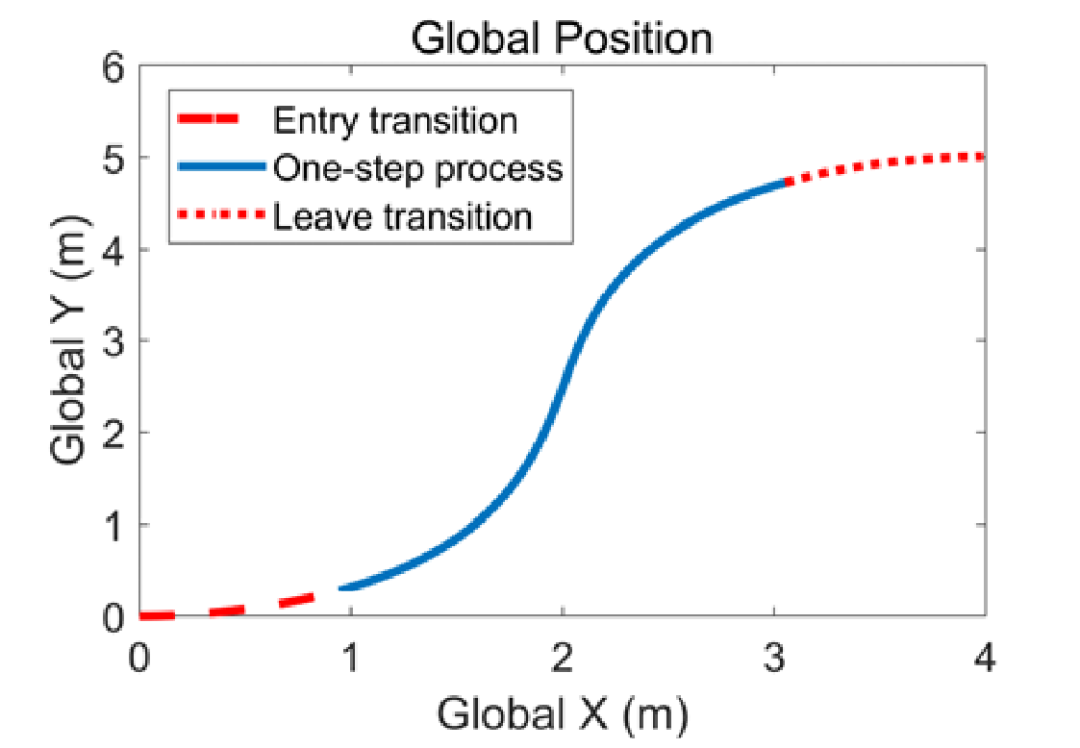
图2 横向运动过程的路径形状
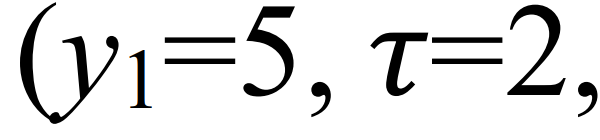
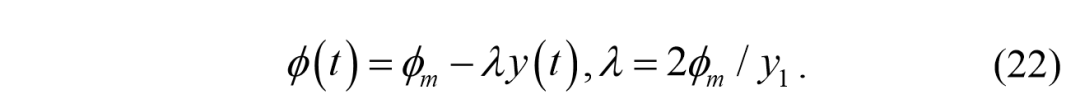
但是,仍然不能保证正速度曲线,除了条件(16)始终成立,这等于,
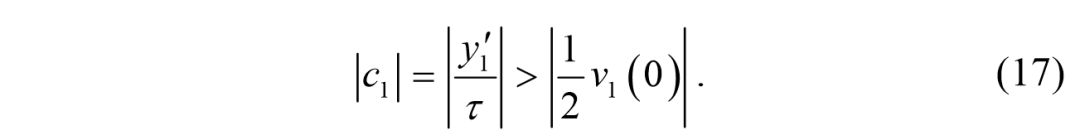
在这里,
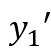
是在一步正弦过程期望的横向位移。如果我们把跃迁路径看作半径为
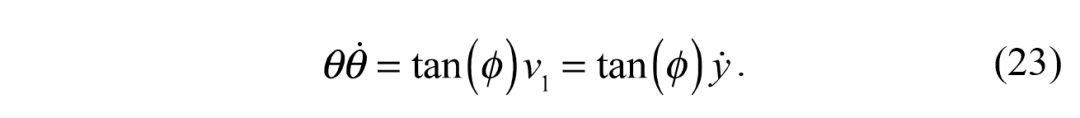
的一对圆弧,我们就得到了
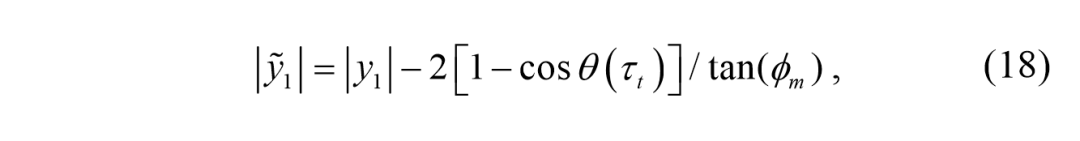
其中,一步过程前后的车辆方向角如下所示,
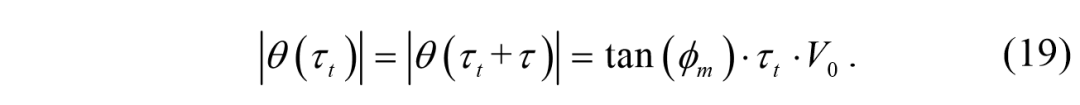
两端的横向车速是,
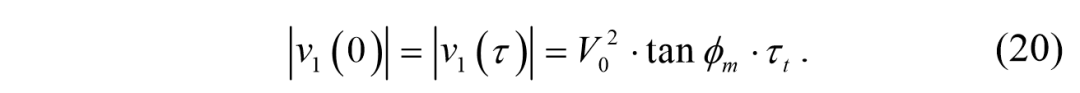
结合(17) ~ (20) ,我们有
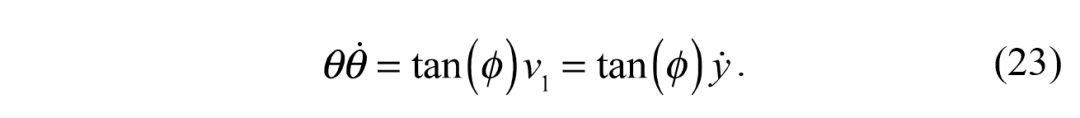
我们从表达式中注意到,如果我们选择

接近于0,这个约束就消失了。通过引入额外的设计参数

,使τ与
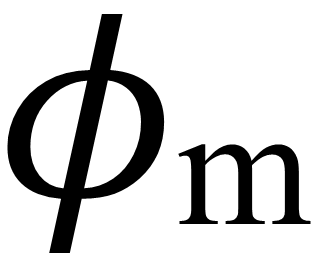
之间的关系解耦,正转速约束从(14)转移到(21)。
3 可达性问题采用本文提出的横向 MP 方法,如果目标值
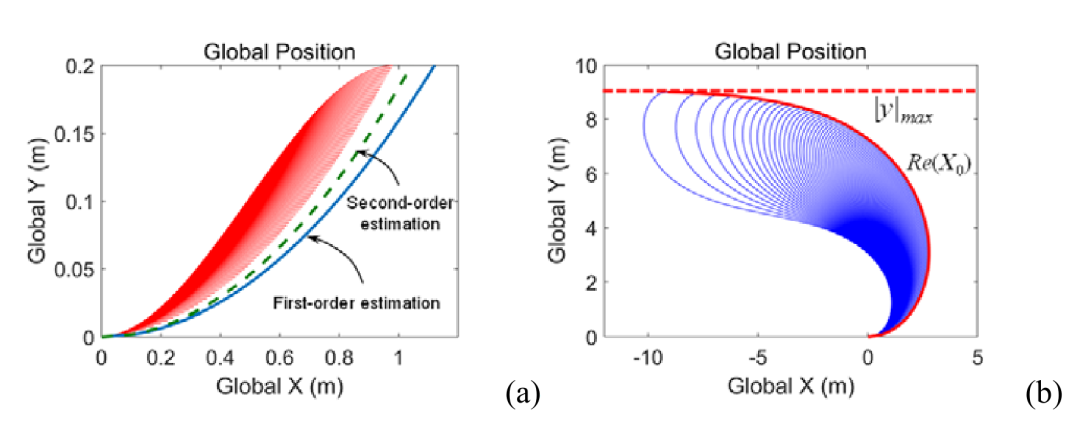
很小,我们总是可以选择适当的
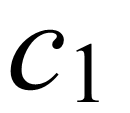
值以精确地保证车辆的横向运动。当

很大时,问题就出现了,因为目标横向位置的大值会增加这段时间内车辆的最大方向角。如果系统(4)中的状态α超出要求的间隔,则链式车辆系统不再合理。此外,目标的纵向位置是下界的最终值x后的一步过程。不幸的是,尽管车辆运动学模型足够简单,但x的最终值应该是通过数值积分获得的,这给该方法的在线应用带来了困难。但是,无论转换如何,一步过程的输入都具有类似的结构。基于这一特征,我们给出了路径函数y = G (x)的一个解析估计。应用
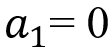
和
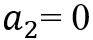
,
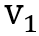
和
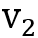
的控制规则是线性相关的,我们可以表示相应的状态y和φ如下,
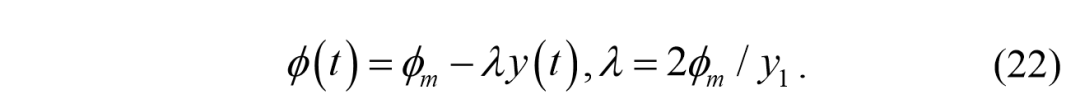
如果状态θ的变化接近于零,我们可以用θ来估计sin (θ)的值。然后考虑从系统(4)中得到的下列方程,
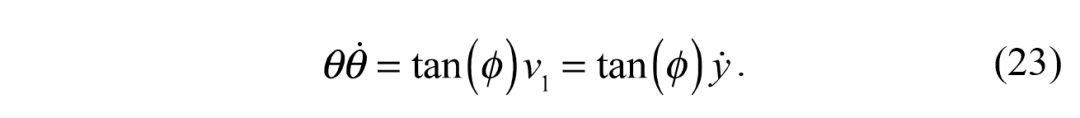
然后,我们使用tan(
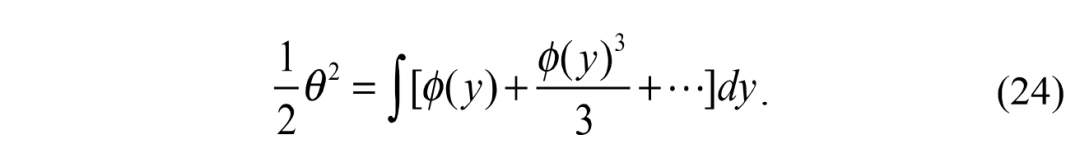
编辑推荐
最新资讯
-
中汽中心工程院能量流测试设备上线全新专家
2025-04-03 08:46
-
上新|AutoHawk Extreme 横空出世-新一代实
2025-04-03 08:42
-
「智能座椅」东风日产N7为何敢称“百万级大
2025-04-03 08:31
-
基于加速度计补偿的俯仰角和路面坡度角估计
2025-04-03 08:30
-
《北京市自动驾驶汽车条例》正式实施 L3级
2025-04-02 20:23





 广告
广告





























































