到上一篇公众号文章《试验模态（四）——模态振型》为止，我们已经基本涉及了模态理论相关的所有概念，完成了MDOF系统模态理论主要内容的阐述。如上篇文章中所谈及，模态理论的推导有两种数学方法，得到的模态参数虽各有异同。然而无论哪种理论方法，所反映的结构模态本质一定是相通的。

本篇文章的目的，首先是讲清楚两种数学方法所得到的模态参数之间的内在联系，其次展示所有这些模态参数在某商业软件中的体现，希望能为结构振动/模态工程师的工作带来一些帮助。

—— 1#老枪

1

模态理论的两种推导方式

对于模态理论的推导，如图1所示，大体上有以下两种方式：

第一种方式基于复变函数数学理论（图1左侧），也就是本公众号近几篇文章所主要采用的方式。基于MDOF系统运动学方程的Laplace变换，从动刚度矩阵求逆的传函表达形式出发，首先由动刚度矩阵行列式的零点，确定出传函的极点；再基于留数定理，将传函变形为留数/极点表示的部分分式形式，并进一步由留数引出模态振型的概念。最终，引入载荷向量，推导得到“结构振动响应为各阶模态振型线性叠加“的结论。

第二种方式，也是绝大部分模态相关书籍所采用的方式（图1右侧），首先从求解MDOF系统自由振动微分方程入手，将微分方程变换为广义特征值问题；求解得到特征值（模态极点）、特征向量（模态振型）；结合模态正交性，证明模态线性叠加理论；最后，推导出广义模态参数（模态质量、模态刚度、模态阻尼）及振型的频响函数表达形式。

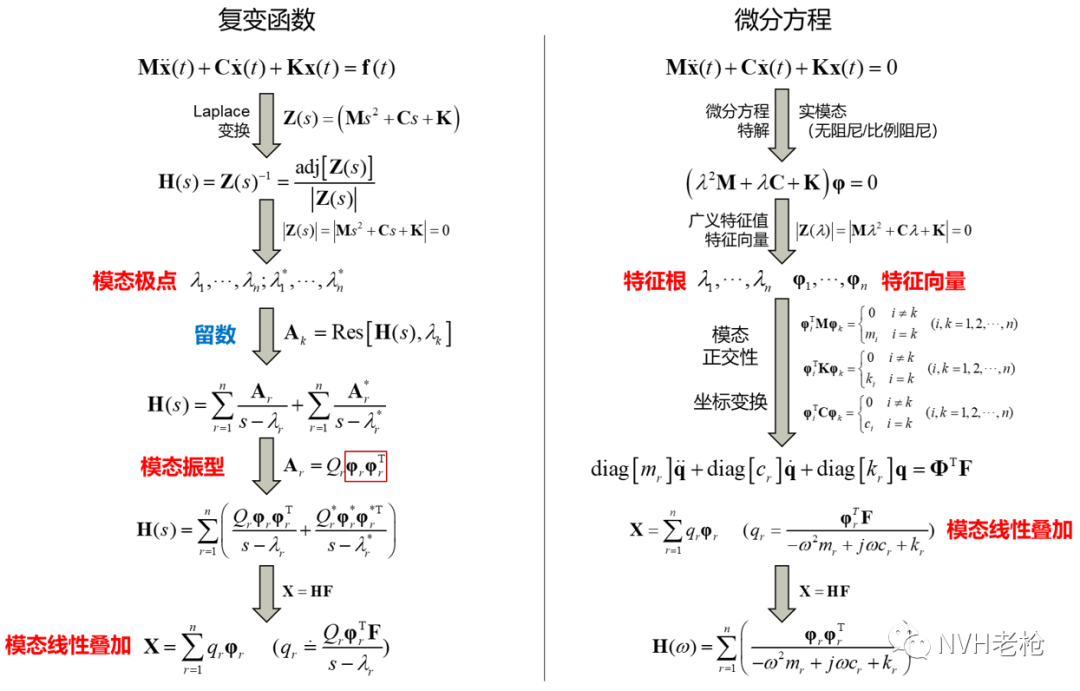
图1 模态理论的两种阐述过程

基于复变函数理论的推导过程，无需考虑系统的阻尼类型，或者说无论是实模态还是复模态，其所有结论都具有普遍意义。但其中关于模态极点的获取，需要求解高阶方程|Z(s)|=0。而高阶方程（≥5阶）的求解，往往难以通过代数方法直接实现，常用的方法仍是将其转换为矩阵特征值问题，用数值方法进行求解。

反观基于微分方程求解的推导过程，虽然基于矩阵的求解便于计算，但从特征值/特征向量求解一开始，就限定于实模态（无阻尼或比例阻尼），因此很多结论就只适用于实模态。例如，关于质量/刚度/阻尼的模态正交性，以及基于这些模态广义参数的模态线性叠加表达形式，理论上严格来讲，都仅限于实模态。

实际上，对于具有一般粘性阻尼特性结构的复模态而言，振动微分方程的求解需要通过额外构建状态方程来完成。此时，模态正交性所对应的将不再是模态质量、模态刚度，而是抽象的广义模态参数a和b（br / ar =－λr）。当然，系统响应仍然满足模态线性叠加理论，表达形式如下（具体推导过程可参考文献1）：

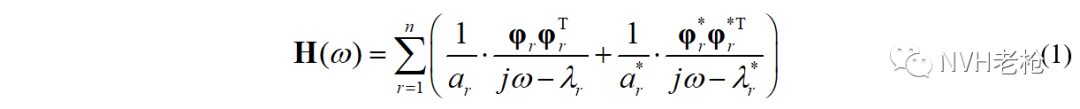
公式(1)和(2)是通过微分方程求解所得到的复模态的普遍表达形式，将其与复变函数方式推导得到的结论相对比，可以发现，模态参数a和比例因子Q互为倒数。

这里，需要说明的是：虽然在现实中，所有结构的模态都是复模态，实模态只是一种理论假设，但在工程中，大多数情况下我们仍然使用的是实模态理论。例如对结构进行模态仿真计算，大部分场合都是做实模态分析。这是因为如上篇文章所述，结构的阻尼参数往往难以精确确定。工程上往往先通过实模态，将结构的质量、刚度特性明确下来，而后再结合试验模态结果，将结构的阻尼信息引入模型，进行下一步的结构动态响应分析。

图1中的两种方法，虽然采用的数学方法不同，但最终所反映的模态本质是相同的，因此二者之间必然有内部的联系。首先，复变函数中的极点求解，与微分方程中的广义特征根是完全对应的，都是求解动刚度矩阵行列式的零点。然而：

1）模态振型的求解过程是不一样的，前者从留数矩阵A中直接得到，后者对应特征向量。既然最终对应的是同一组参数，那么两者到底存在怎样的内在关联？

2）如前所述，我们知道复变函数方法中的比例因子Q与复模态微分方程求解中的模态a互为倒数，但二者都是没有明确物理意义的抽象参数。而通过实模态正交性所得到的广义模态参数（mr，kr，cr），可以把结构频响或振动响应表达为多个SDOF系统的线性叠加。显然，后者比前者更具有直观的物理意义。那么比例因子Q与广义模态参数之间又是怎样的关系？

下面，我们就上述两个问题分别进行阐述。

2

留数矩阵A与特征向量φ的关系

传递函数矩阵与动刚度矩阵的关系为：

我们在《试验模态（三）——留数的概念》中提到，对于n自由度系统，行列式| Z(s)| 是最高次项为s2n的多项式。

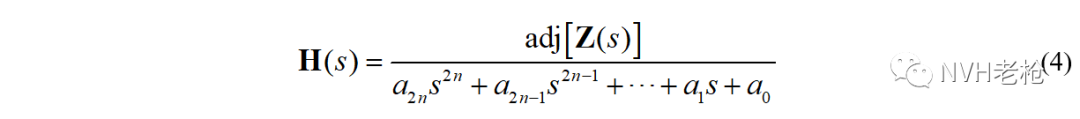
将分母多项式分解为极点表达形式，则为：

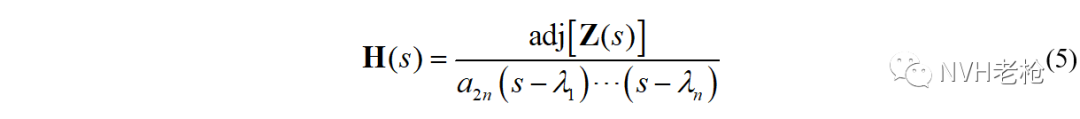
用《试验模态（三）——留数的概念》中的求极限方法（规则I）求取各阶留数矩阵，如第r阶留数为：

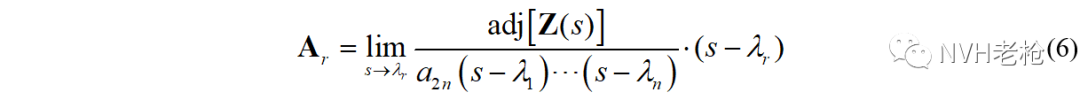
可以看到，式(6)中除伴随矩阵之外的部分为一个常系数，将其定义为Pr：

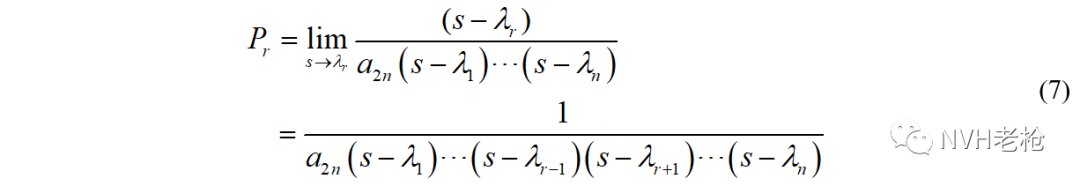
则有：

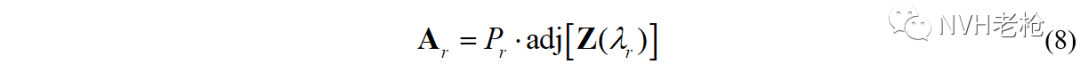
因为极点λr是|Z(λr)|的零点，因此有：

将式(9)和微分方程方法中广义特征值/特征向量的求解方程(10)相对比：

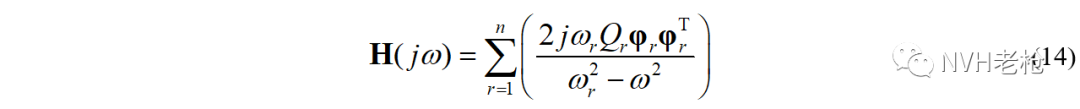
就会理解:adj[Z(λr)]中的每一列，都应与特征值λr所对应的特征向量（振型）成线性比例关系。设二者相差一个系数Kr，考虑到留数矩阵为对称矩阵，则有：

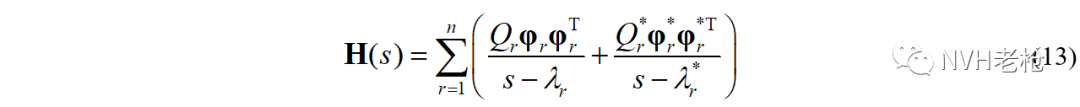
将两个常系数Pr，Kr乘积合并为一个常系数Qr（比例因子），得到：

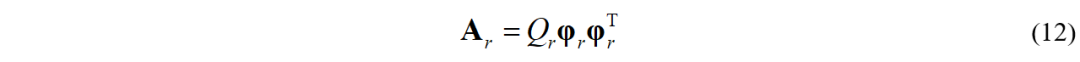
到此，我们就完成了留数矩阵A与特征向量（振型）φ之间关系的严格推导。

2

比例因子Qr 和模态质量mr 的关系

在通常情况下，试验模态分析得到的结果都是复模态，模态参数理应包括：模态极点/特征值λ，留数A，模态振型φ，比例因子Q，模态a，模态b等。然而，实际上在模态分析软件中仍可得到实模态所对应的广义模态参数（模态质量mr、模态刚度kr、模态阻尼cr）。

这个过程是：通过试验模态参数识别得到极点及留数矩阵后，先选择一定的振型归一化方式，确定出各阶模态的振型向量及比例因子Qr；而后认为结构近似于实模态特性，根据实模态下比例因子Qr和模态质量mr的关系，取Qr的虚部换算出各阶模态质量以及模态刚度。下面我们就具体说明：实模态条件下，比例因子Qr和模态质量mr的对应关系。

MDOF系统传递函数矩阵的极点/振型表达形式为：

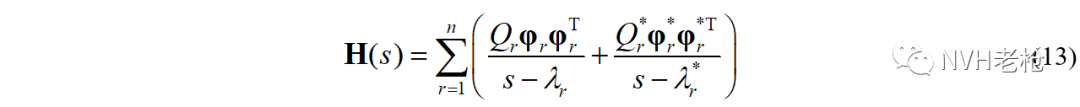
对于实模态而言，阻尼为0，极点为纯虚数，模态向量为纯实数，比例因子为纯虚数。因此有：λr= jωr，λr*=－jωr，φr* = φr，Qr*=－Qr。取 s =jω，得到频响函数矩阵：

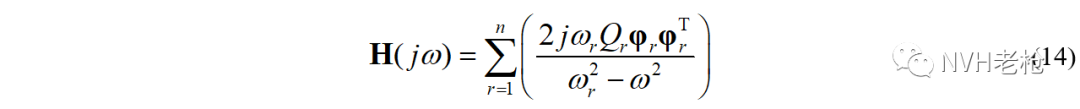
以及结构的振动响应：

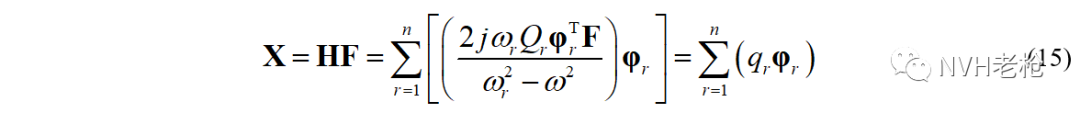
其中模态坐标qr为：

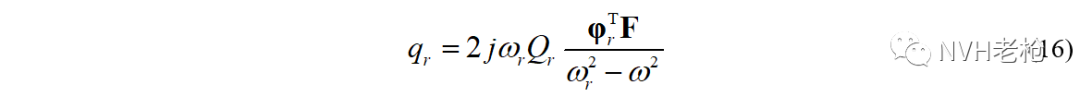
而根据上篇公众号《试验模态（四）—模态振型》公式(22)，由实模态正交性得到的模态坐标为：

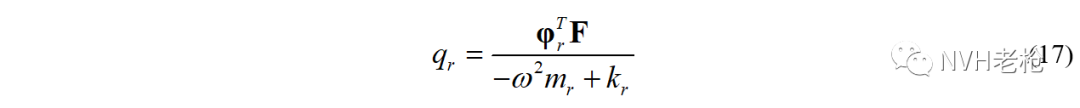
将上式右侧分子分母同时除以mr，并根据kr / mr= ωr2，得到：

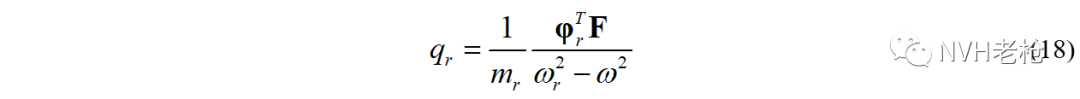
为方便观察，我们将公式(16)和(18)放在一起：

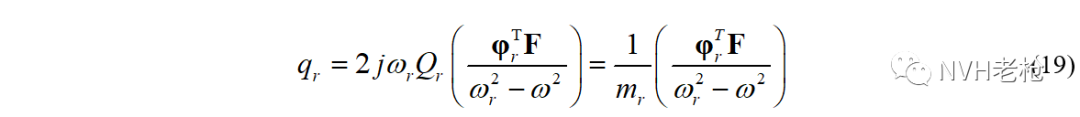
可以看出比例因子Qr与模态质量mr的关系为：

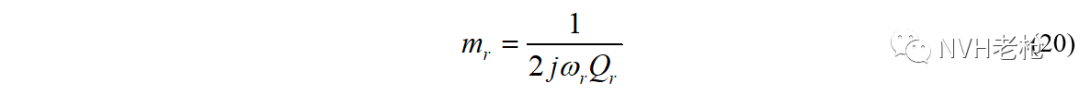
例如，以《试验模态（四）——模态振型》中的2DOF系统为例，两阶固有频率为：ω1=5 rad/s，ω2=  rad/s，当两阶振型表示为  和  时，比例因子  ，  。而根据模态正交性得到的模态质量为：m1=5.5 kg，m2=11/9 kg。不难验证，比例因子Qr和模态质量mr的关系的确满足式(20)。

在试验模态分析中，通过选择某种振型向量归一化方式，确定出各阶模态的比例因子Qr，然后根据公式(20)计算出模态质量，再进一步得到模态刚度kr = mr ωr2。而模态阻尼cr，我们在上一篇已提到，可直接通过该阶模态的临界阻尼比ξr计算得到：cr = 2ξr mr ωr。至此，我们就得到了所有广义模态参数。

注：对于公式(19)，因为：  ，括号中的后半部分为单调递减函数。以图2固有频率为10Hz为例，可以看到后半部分（蓝色曲线）随着频率上升，快速衰减。当频率接近固有频率附近时，后半部分更远小于前半部分，通常可以忽略。因此有：  ，所以公式(19)中的模态坐标可简化为：  

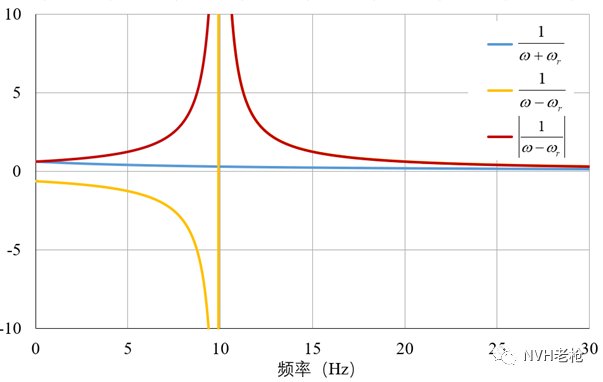
图2 模态坐标的简化说明

实际上，在上篇公众号文章《试验模态（四）——模态振型》模态线性叠加理论部分，我们提到传函的后半段共轭部分可省去，其原因与上类似。

4

试验模态分析软件中的模态参数

下面我们来结合某经典的试验模态分析软件，说明具体在哪里可以查看到各个模态参数。

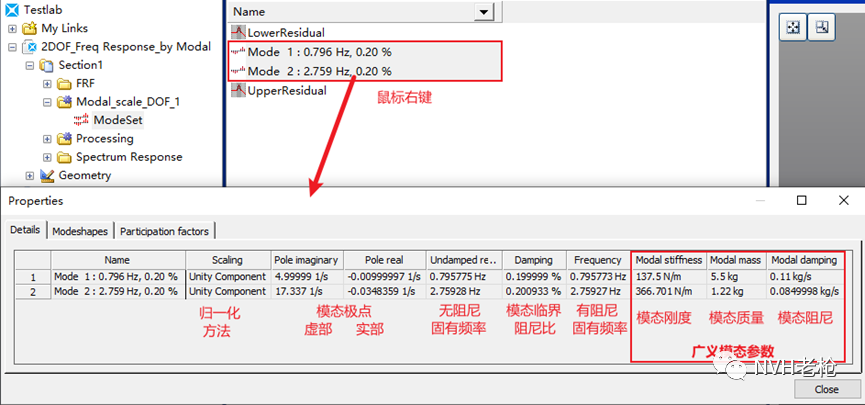
在Navigator的模态分析结果中，选中要查看的模态，鼠标右键选择Properties菜单，就会弹出该阶次模态的属性框。

首先在第1个Details标签页，我们依次能看到振型归一化的方法（Scaling）、模态极点（Pole）、无阻尼/有阻尼固有频率（Undamped resonance Frequency/ Frequency），以及模态临界阻尼比（Damping）。

而对于广义模态参数，如前所述，由比例因子Q决定，因此采用不同的归一化方法，其值也将不同。关于不同的归一化方法，读者可参阅《试验模态（一）模态分析的归一化和意义》。

图3即为我们一直使用的2DOF系统例子，所对应的模态参数及广义模态参数，振型归一化方法采用Unity Component方法（将DOF:1自由度振型系数置为1，振型向量同比缩放）。大家可自行与《试验模态（四）——模态振型》中的计算结果进行对比。

图3 试验模态软件中的模态参数（1）—极点、频率、阻尼及广义模态参数

（P.S. 在上篇文章中，自然频率f与圆频率ω的转换在excel中不留神把两列弄反了，因此在两阶振型动画，以及图1的模态叠加法振动响应分析结果中，f (Hz) 的值是错误的，应除以4π2，在这里为给各位读者造成的困扰致歉，恳请大家谅解。）

在Details标签页，虽然没有比例因子Q，但可以查看到模态a（ModalA）。如前所述，二者互为倒数关系。图4中可以看到模态a的实部通常都很小，接近于纯虚数。

此外，软件还提供根据振型向量计算得到实模态验证结果，包括：各自由度的相位分散程度（Scatter），平均相位偏移（Mean phase deviation，MPD）以及相位共线性（Modal phase collinearity，MPC），以帮助客户判定该阶模态近似于实模态的程度。

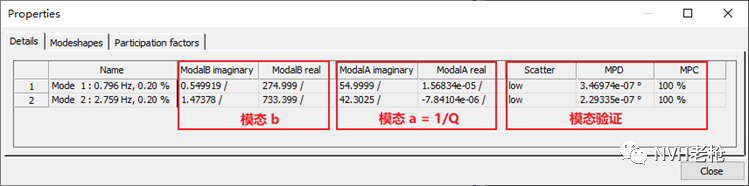
图4 试验模态软件中的模态参数（2）—模态b和模态a，及实模态验证

在下一个标签页Modeshapes中（图5），我们将看到分别以幅值/相位及实部/虚部表示的各阶模态振型向量。通常来说，可以看到模态振型的虚部相比较实部很小，接近于实数向量。相位接近于0°（同向）或180°（反向）。

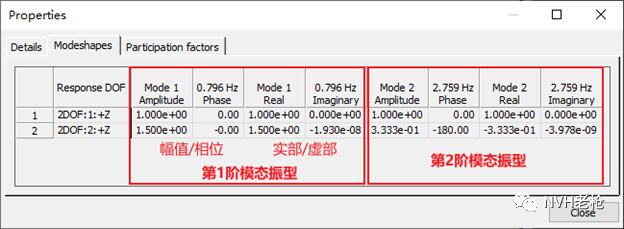
图5 试验模态软件中的模态参数（3）—模态振型

对于第3个标签页的模态参与因子（Participation factors），在大部分振动或模态书籍中没有这个概念。模态参与因子用于多参考模态分析中，可以用于模态试验激励充分性验证。限于篇幅，我们暂且留待以后再介绍。

除了以上模态参数之外，在软件的Modal Validation界面，还可以查看留数A（Residues）。与比例因子及模态a一样，当结构越趋近于实模态特性，留数也将越趋近于纯虚数。

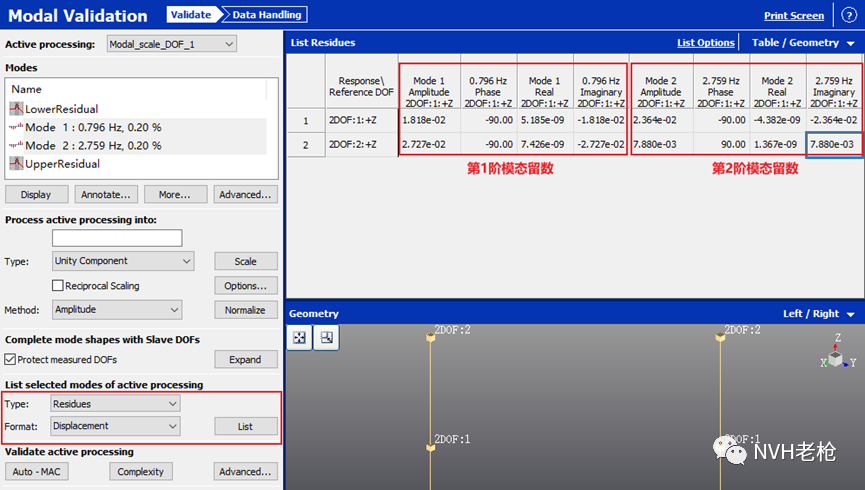
图6 试验模态软件中的模态参数（4）—留数

综上，在结构趋近实模态特征时，就所有模态参数的实/虚特性，简单总结如下（“→”表示“趋近于”）：

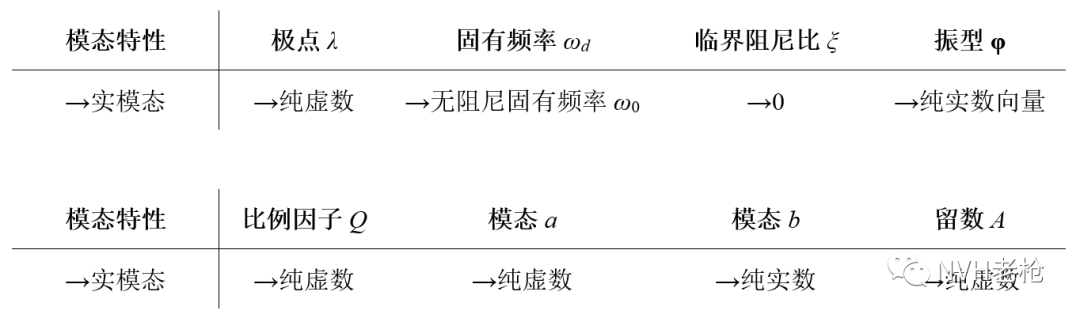
5

小结

这篇公众号文章的主要目的在于：对于模态理论的阐述，实际存在两种数学理论，而这两种理论会产生不同的模态参数或概念。比如，国内外大部分模态书籍，都是微分方程求解的思路。因此，很可能读者翻遍整本书，会发现很多模态概念（比如极点、留数、甚至比例因子）根本就找不到，或只是被用类似于“这个参数被称为…”这样的一句话带过。这就造成工程师在使用模态相关的工程软件时，很多参数无法理解。

即使有些书（如笔者本篇文章的主要参考文献[2]）会从复变函数的角度讲解，但可惜文字阐述非常精炼，对于初学者不是很友好，且也未能将两种不同理论的区别与联系完全说清楚。比如试验模态分析得到的复模态分析结果，为什么还能对应出本应实模态才有的模态质量、模态刚度这些参数。

鉴于上述原因，尽管试验模态技术已经在国内应用了20余年，然而工程师在使用工程软件过程中，往往还是只能停留在频率、阻尼、振型这三个最基本的模态参数的层面，无法实现模态数据更深层次的应用。举例来说：通过试验模态分析得到的广义模态参数，实际上工程师无需使用CAE软件，通过模态线性叠加，就可以直接对结构各部位的动力学响应进行预测。这一点恐怕是大多数工程师没有意识到的。

因此，在本篇公众号文章中，笔者试图通过以下几方面，帮助读者理清脉络：

• 简要说明了模态理论两种阐述方式的区别：基于Laplace变换复变函数理论推导得到的结论适用性广（无论实模态还是复模态均使用）；而实模态假设下的微分方程求解虽然有一定局限性，但所得到的基于广义模态参数的SDOF系统线性叠加结论，其物理意义更为明确。

• 虽然数学方法不同，但最终的模态本质是一样的，就两种方法的内部关联进行了分析说明。对留数矩阵与特征向量关系进行了严格推导，并明确了比例因子与模态质量的关系：mr = 1 / (2jωrQr)。说明了如何从试验模态分析所得到的复模态分析结果中，进一步计算得到各项广义模态参数（模态质量、模态刚度及模态阻尼）。

• 结合试验模态分析的某商业软件，说明了在哪里可以查看到各项模态参数。（如果大家对最近几篇文章所使用的2DOF示例数据感兴趣，可发邮件至3630073941@qq.com索取，或直接申请QQ好友，会不定期发送。P.S.数据为2021版本的项目文件，需要有相对应版本的软件才可以打开。）

文章一旦牵涉理论，总是难免大量公式。但对于致力于想把模态弄明白的朋友，笔者相信，通过本公众号相关的几篇文章，认认真真多读几遍，您一定会有别样的收获。如有问题需要探讨或指正，请发邮件至上述邮箱与笔者交流。

疫情已近三年，希望“大疫不过三”即将实现。祝大家远离病毒，身体健康。我们下篇文章再见。

参考文献

[1]李德葆, 陆秋海. 实验模态分析及其应用[M]. 科学出版社, 2001.

[2]沃德·海伦等. 模态分析理论与试验[M]. 北京理工大学出版社, 2001.