纯跟踪算法用于无人车自动泊车

目的

使用简单的“纯跟踪算法”实现无人车自动泊车或者位姿调整。在泊车或者工业场景，如果空间不够，那么车辆经常需要做一些大角度的转向或者倒车，例如叉车。

这些场景与一般的道路行驶场景可能有所区别，道路行驶一般只考虑前进方向的高速行驶，并且转向曲率不会太大。泊车场景恰好相反，曲率大、速度慢，而且伴随行驶方向的变化。

道路行驶下的跟踪已经被研究的比较深入了，那么道路行驶使用的跟踪算法还适用于倒车场景吗？本文我们来研究一下这个问题。

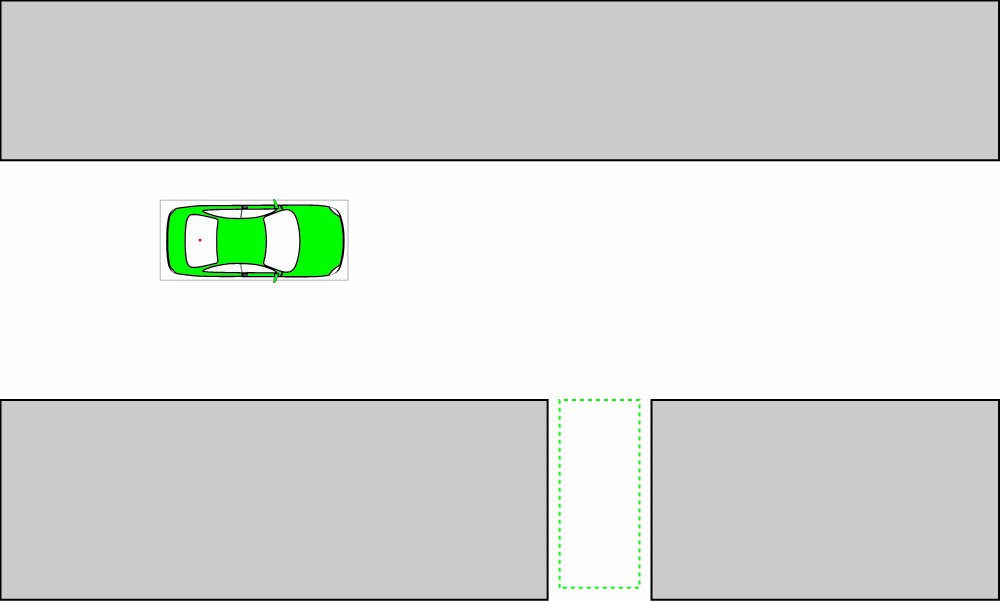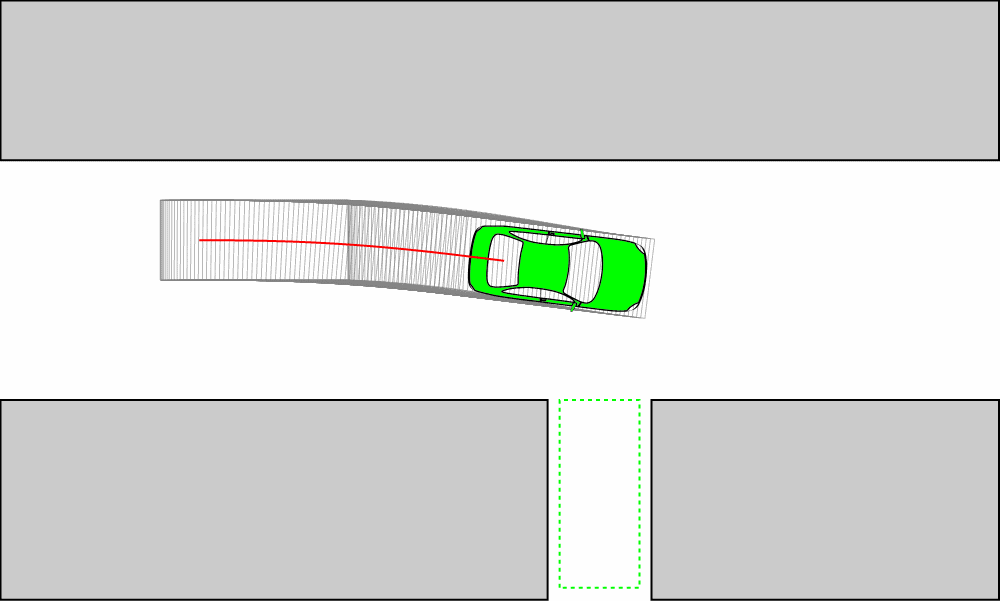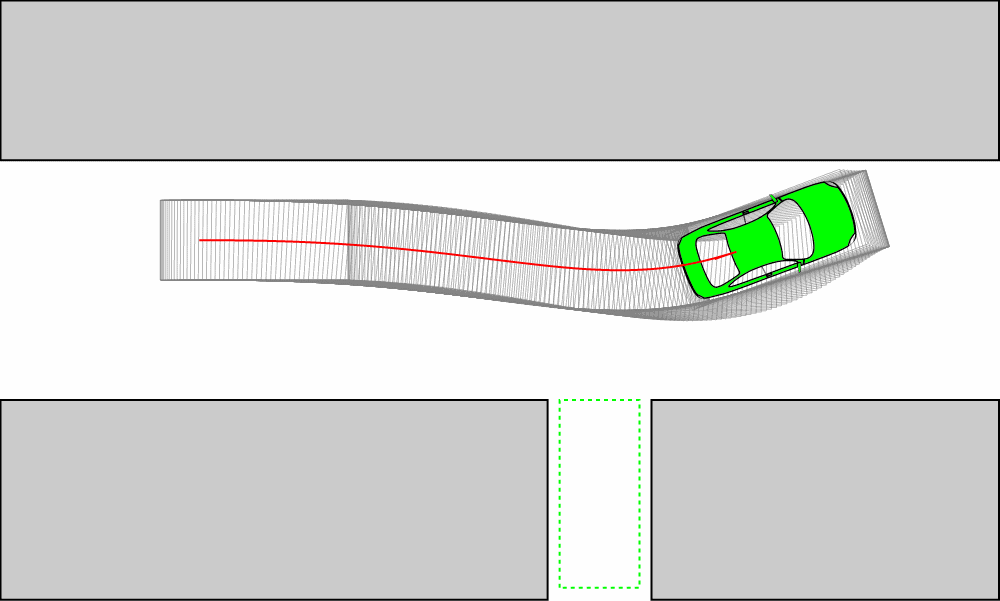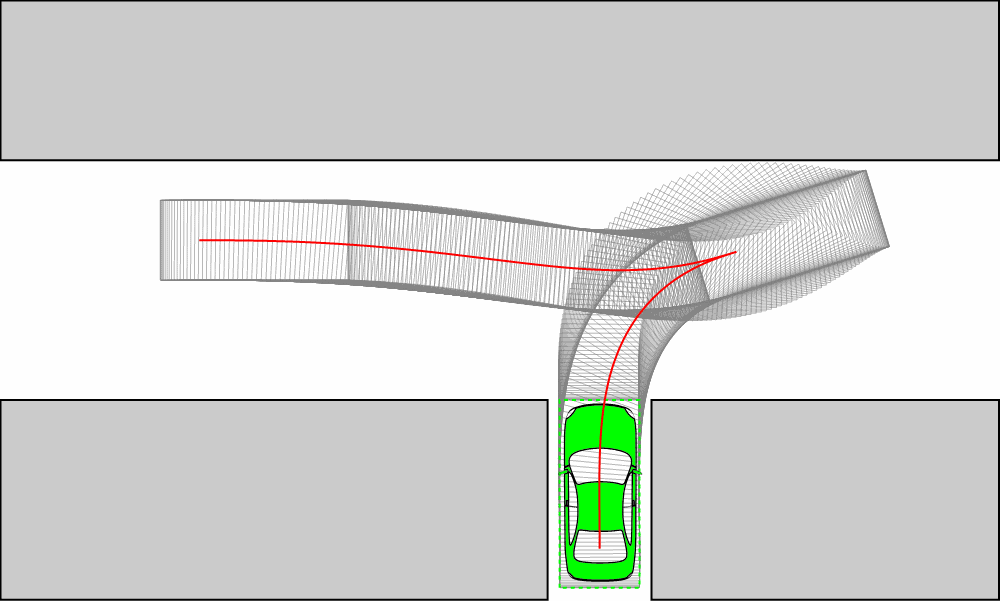
Reeds-Sheep曲线

假设无人车的运动路径是已知的，笔者使用 https://github.com/hbanzhaf/steering_functions 中提出的曲率连续的改进Reeds-Sheep曲线生成路径。

程序输出的路径是一系列离散的点，点之间的距离可以自定义，笔者选择每5毫米一个点，程序中设置DISCRETIZATION=0.005。

路径采用nav_msgs::Path消息发出。

纯跟踪算法

纯跟踪算法（Pure Pursuit）首先要指定一个被跟踪的目标点。

原始版本的纯跟踪算法只讨论了跟踪无人车前方的点，对于Reeds-Sheep曲线这种包含运动方向变化的曲线，无人车既需要前进也需要后退，但是想实现后退也非常简单。

笔者将被跟踪的目标点称为局部目标（local goal）无人车真正最终的静态目标点则称为全局目标（global goal）。

纯跟踪需要无人车的定位，仿真时假设这个定位信息由ROS中的/base_pose_ground_truth消息给出。局部目标的计算方式是，遍历路径，找到第一个离无人车≥ d l 的路径点。

d l 就是前视距离，d l 越小跟踪精度越高，但是越容易导致震荡。机器人在运动时，这个局部目标也会更新。

如果找到的局部目标落在了无人车的后方，此时意味着无人车需要后退，只需要将速度取负值即可，前轮转角不用变。

出现的问题

1.转折点

在仿真时出现了一些问题。首先，最困难的是对于尖点（cusp）怎么处理。因为很多情况下，Reeds-Sheep曲线都包含尖点，在尖点处车辆会改变运动方向。

如果使用纯跟踪算法跟踪这个路径，那么在尖点处会出现一个问题。因为纯跟踪算法总要指定一个跟踪点，这个跟踪点一般在车辆前方或者后方一定距离（d l ）处。

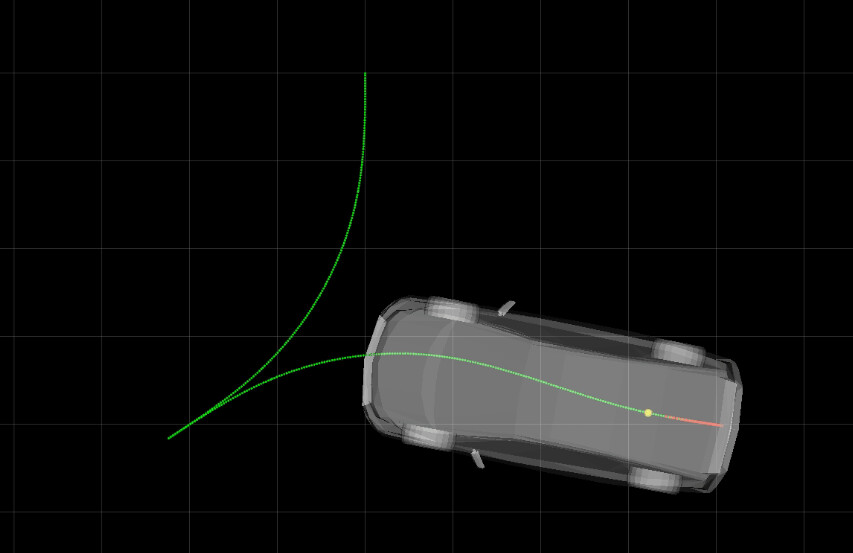
在向尖点运动时，车辆不会正好处于尖点上，而是提前离开。下图中的d l = 0.2后面也采用这一数值。

图中的黄点是被跟踪的局部目标，红色点表示无人车后轮轴中心处的实时位置。

这就导致车辆没有完全位于路径上，进而导致后面的跟踪出现横向偏差（如下图所示），即使采用曲率连续的Reeds-Sheep曲线版本也没有用。

这是纯跟踪算法本身的问题吗？不是，纯跟踪算法完全可以跟得上，我们为了安全通常把输出角度给限幅了，如果解除限幅你就会发现纯跟踪算法完全可以准确的跟踪。

但是实际使用时我们又不可能解除限幅，所以怎么解决这个问题呢？

一种是直接增大一点Reeds-Sheep曲线的最小转向半径，令其略大于车辆的真实最小转向半径，笔者尝试增加了约10%，跟踪情况如下图。

另一种方法是增加尖点（cusp）部分的长度，这可以通过改变主程序（steering_functions_node.cpp）中的sigma_max_变量实现，sigma_max_越小，过渡部分越长，最好大于d l 试验发现取sigma_max_=0.5左右就可以。

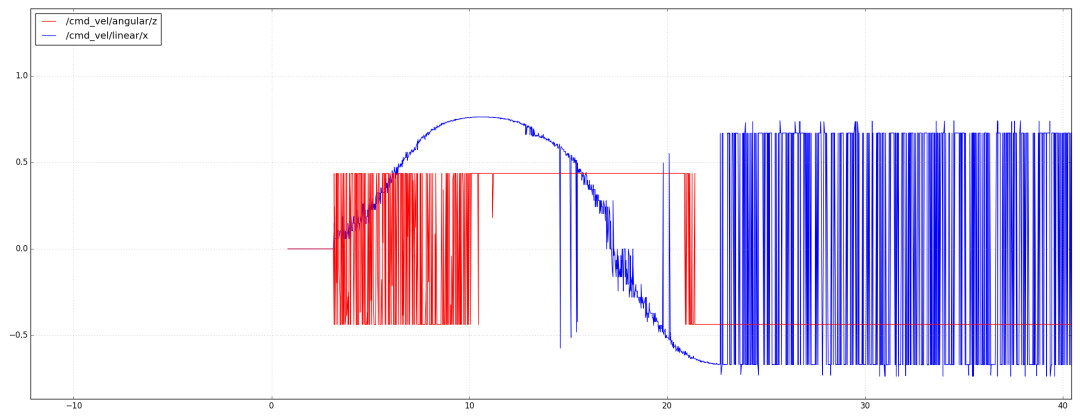
控制指令如下图所示。

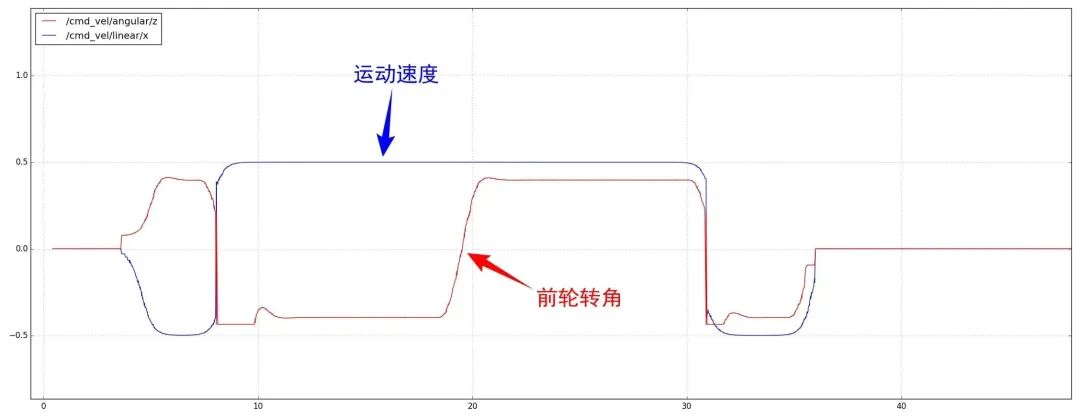
速度单独进行规划，然后叠加到路径上，如下图所示。

2.定位误差

前面的控制都假设定位是完美的，不存在定位误差。如果加入定位误差，纯跟踪算法的表现会怎么样呢？

我们用随机数来模拟定位误差，定位误差一般是正太分布的，因此用正态分布函数std::normal_distribution生成随机数，均值总是取0，标准差决定了误差的范围。

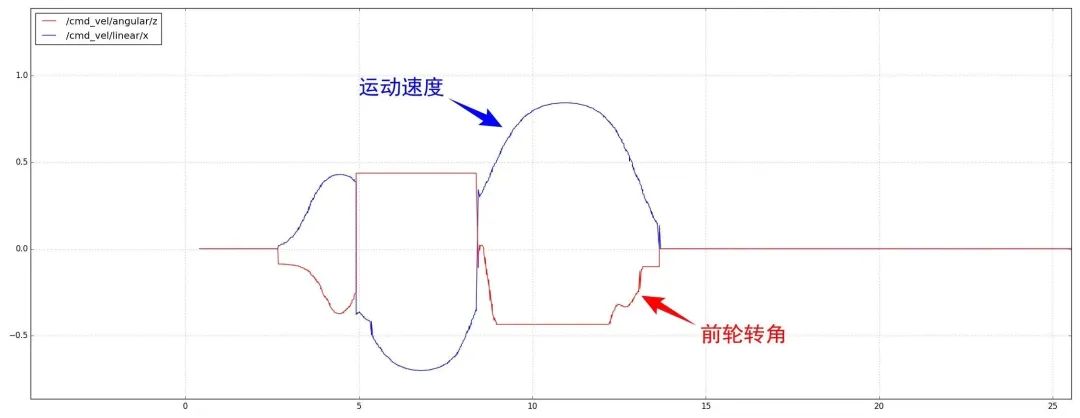
首先取小的标准差—— 1mm，无人车的表现如下图所示，无人车的跟踪效果比较好。

但是前轮转角的变化却非常剧烈，如下图所示。这还仅仅是1mm左右的误差，这在实际中是几乎不可能达到的。

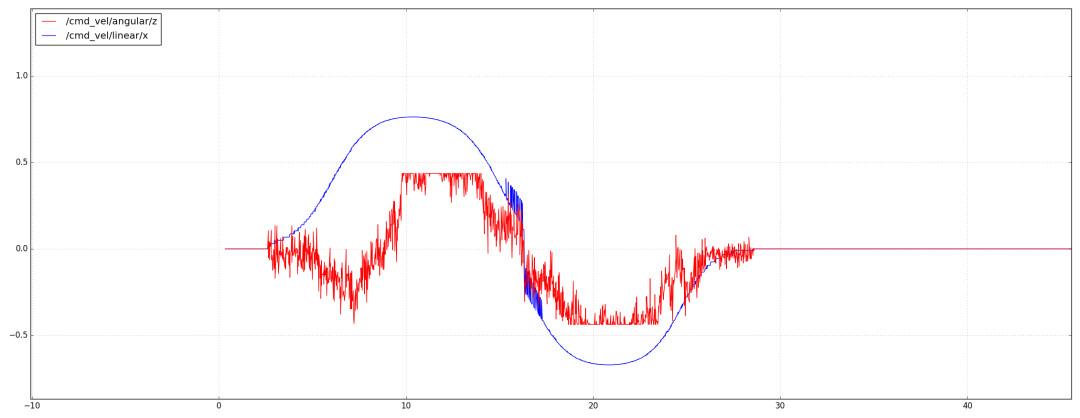
标准差为1cm时的表现如下图所示，已经产生了明显的横向跟踪偏差。

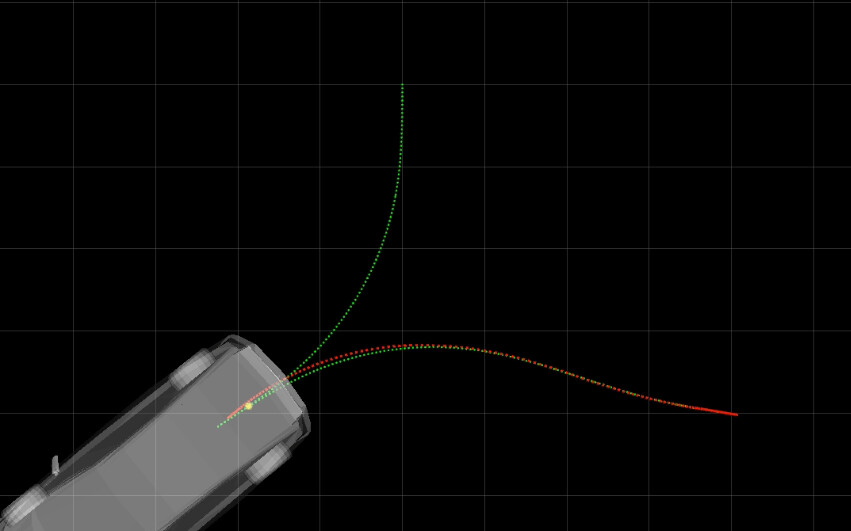
此时前轮转角已经惨不忍睹了，如下图所示，这还是1cm左右的误差，实际中无人车的定位要达到1cm也是很困难的。

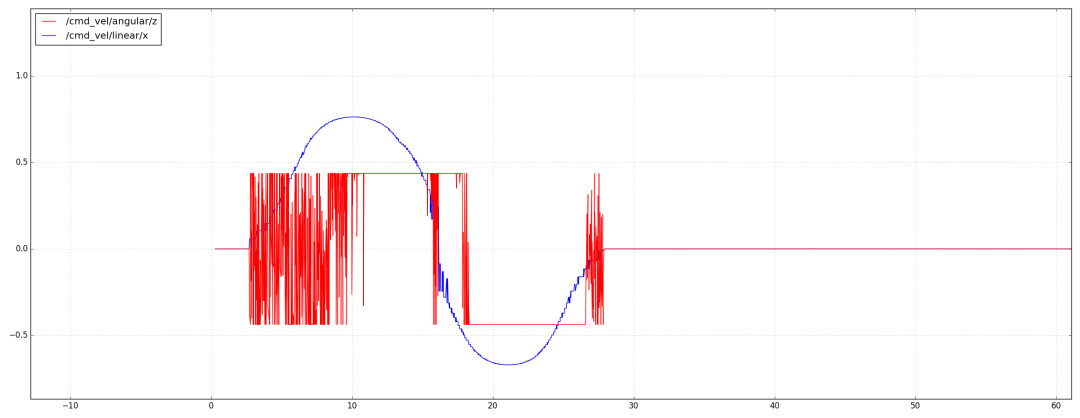
标准差为5cm时的表现如下图所示，这个误差是一般室外卫星定位的误差范围，也就是常见的误差，此时无人车彻底无法跟踪。

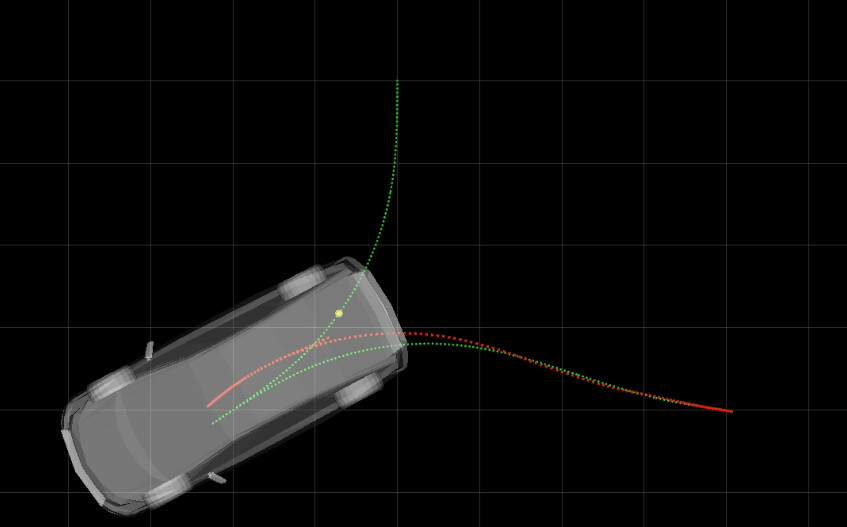
不仅前轮转角更疯狂了，而且由于横向偏差已经超过了前视距离d l ，局部目标已经出现在无人车侧面了，导致无人车完全无法跟踪了，如下图所示。

这说明纯跟踪算法对定位误差是极其敏感的，在实际应用时这是个非常严重的问题。

算法理解

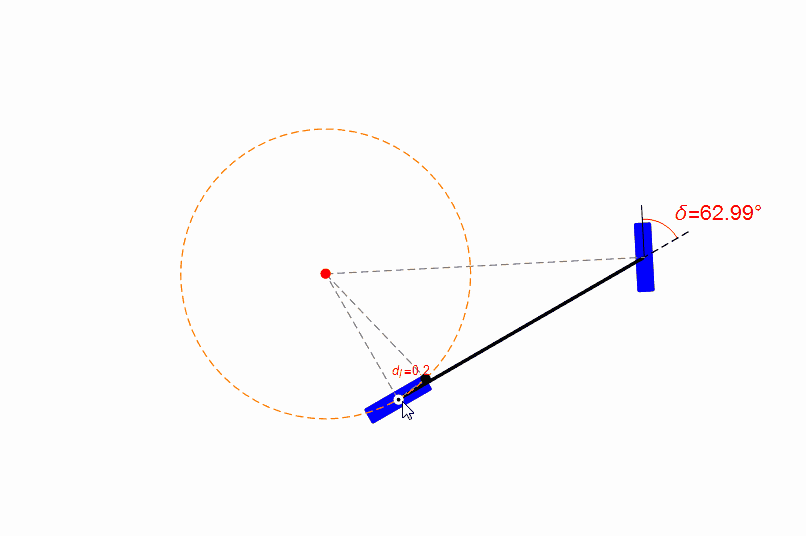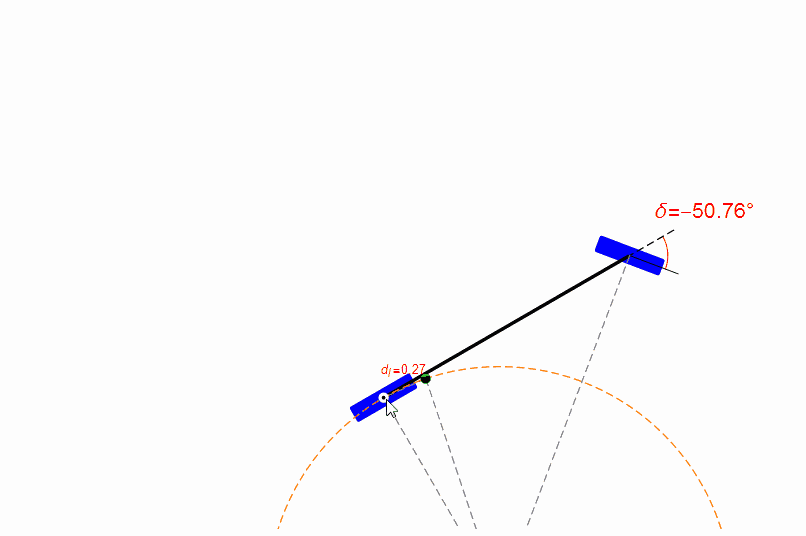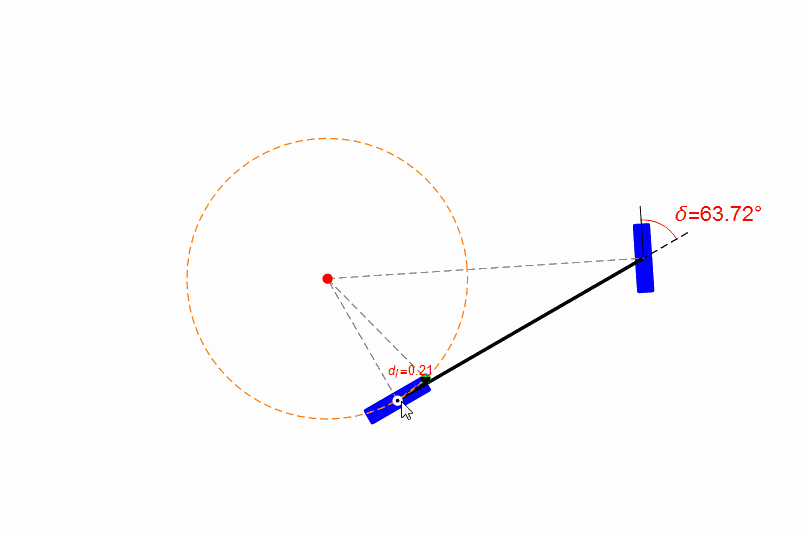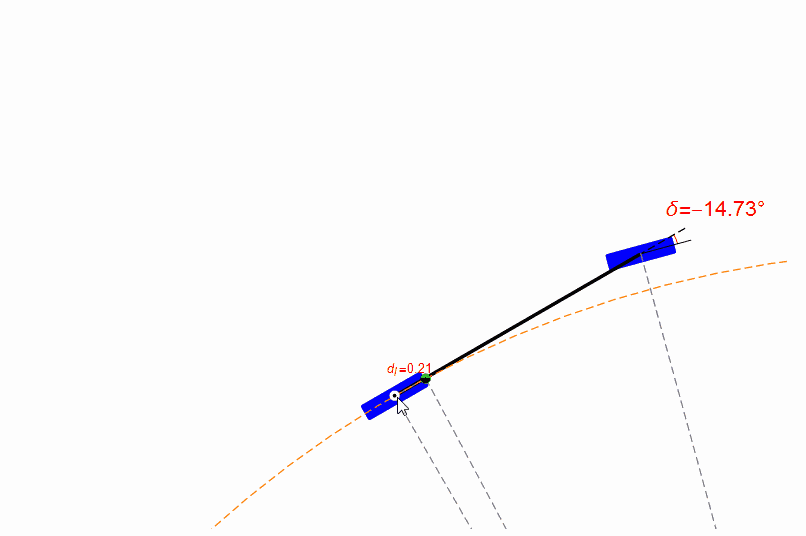
为了易于理解纯跟踪算法，笔者用Mathematica设计了一个小程序，你可以用鼠标拖动目标点（绿色点），并观察前轮的转角，如下图。

目标点是纯跟踪算法中的核心概念，这个目标点是人为设计或者选择的。跟踪性能的好坏不仅取决于控制参数的选择，目标点的选择也起到重要的作用。

当目标点选取的不好时，例如距离无人车当前位置过近，则会出现控制量剧烈变化。

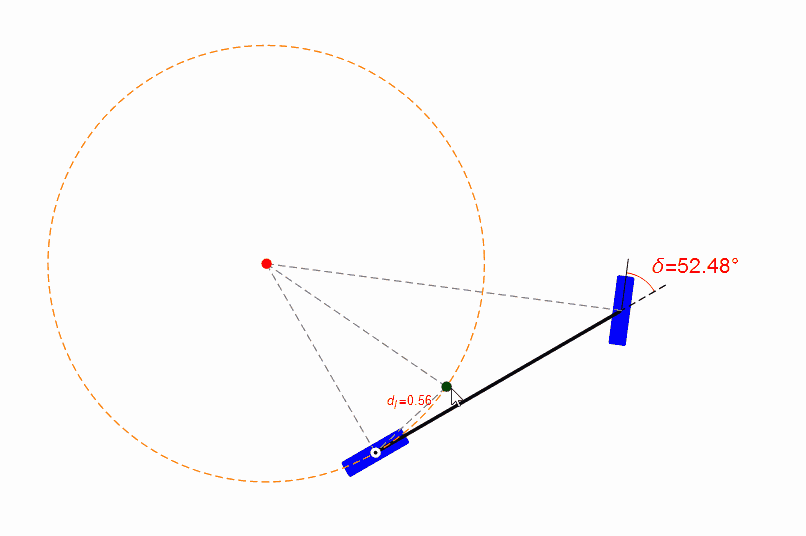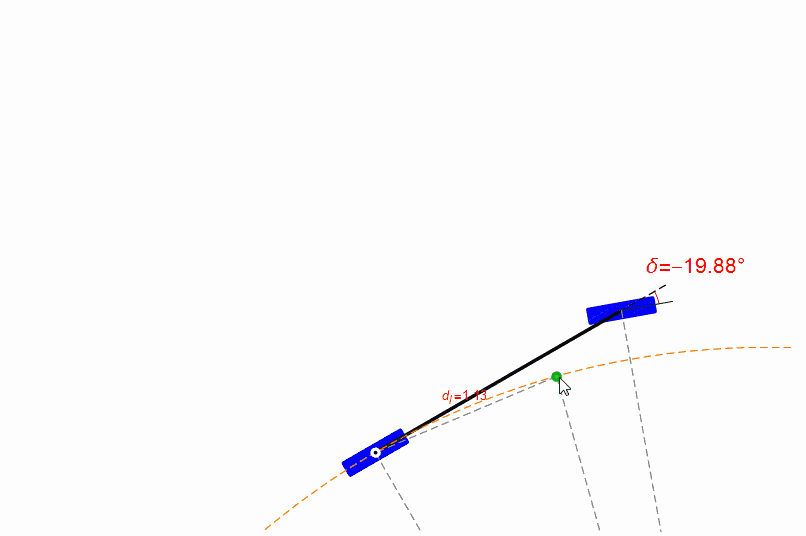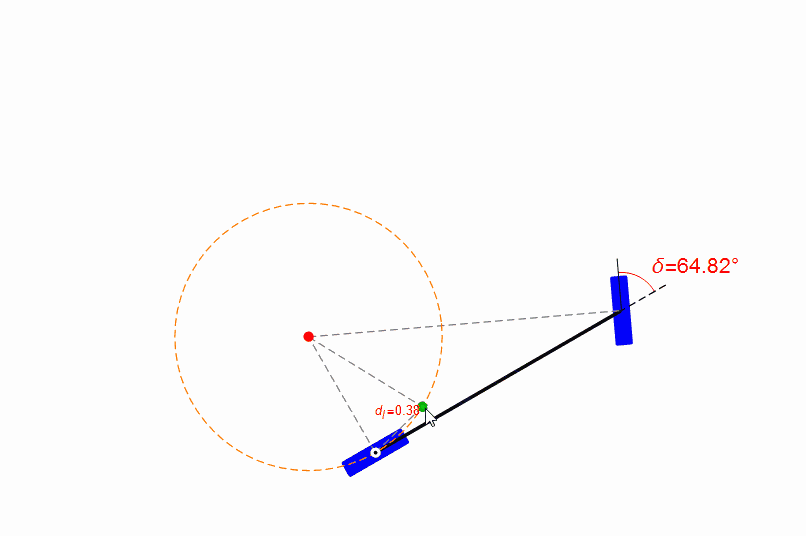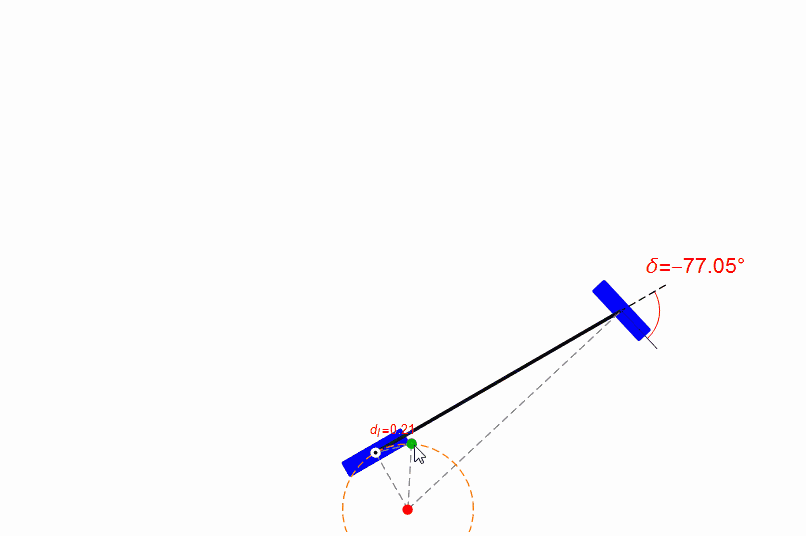
你也可以用鼠标拖动无人车的参考点，观察前轮的转角，如下图。从图中可以发现，在距离目标比较近时，纯跟踪算法的表现很糟糕，参考点位置有一点点改变都会导致前轮转角剧烈变化。

但是无人车的定位本身是必然存在偏差的，所以纯跟踪算法在前视距离短时稳定性并不好。

cuboid[center_: {0, 0}, dim_, radius_: 0] := Rectangle[center - dim/2, center + dim/2, RoundingRadius -> 0.01];
move2D[shape_, pose_] := Translate[Rotate[shape, pose[[3]], {0, 0}], pose[[1 ;; 2]]];
L = 1.64; 
\[Delta]max = 25 Degree ;
bicycle[pose_, \[Delta]_] := {
   rearWheel = cuboid[{0, 0}, {0.4, 0.1}, 0.1];
   frontWheel = move2D[rearWheel, {L, 0, \[Delta]}];
   trunk = cuboid[{L/2, 0}, {L, 0.02}, 0.1];
   move2D[{Blue, frontWheel, rearWheel, Black, trunk, Red, Circle[{L, 0}, 0.22, {0, \[Delta]}]}, pose]
   };
Manipulate[
 pose = Flatten@{p, \[Theta]};
 dirvec = AngleVector[\[Theta]];
 vertvec = {-dirvec[[2]], dirvec[[1]]};
 p1 = p + L*dirvec;
 dl = Norm[goal - p];
 \[Alpha] = VectorAngle[goal - p, {1, 0}] - \[Theta];
 \[Delta] = ArcTan[2*L*Sin[\[Alpha]]/dl];
 R = Abs[dl/2/Sin[\[Alpha]]];
 c = p + Sign[\[Alpha]]*R*vertvec;
 a1 = -VectorAngle[p - c, {1, 0}];
 a2 = -VectorAngle[goal - c, {1, 0}];
 Graphics[{bicycle[pose, \[Delta]], Point[c], AbsoluteThickness[1], 
   Line[{p1, p1 + AngleVector[\[Theta] + \[Delta]]*0.3}], AbsoluteDashing[{6, 3}], Black, Line[{p, p1 + dirvec*0.3}], Gray, Line[{p, c}], Line[{c, goal}], Line[{goal, p}], Line[{c, p1}], Orange, Circle[c, R(*,{a1,a2}*)], AbsolutePointSize[8], White, Point[p], Red, Point[c], Darker@Green, Point[goal], Red, Text[Style[ "\[Delta]=" <> ToString@Round[\[Delta]*180/Pi, 0.01] <> "\[Degree]", FontSize -> 16], p1 + dirvec*0.5], Text["\!\(\*SubscriptBox[\(d\), \(l\)]\)=" <> ToString@Round[dl, 0.01], (p + goal)/2 + {0, 0.1}]}, 
  ImageSize -> 600, PlotRange -> 1.5 {{-1.5, 1.5}, {-0.5, 1.5}}, 
  Axes -> False], {{p, {0, 0}}, Locator, Appearance -> Graphics@Point[{0, 0}]}, {{goal, {0.16, 0.12}}, Locator, Appearance -> Graphics[{Green, Point[{0, 0}]}]}, {{\[Theta], Pi/6}, 0, 2 Pi, 0.01}, TrackedSymbols :> True, Initialization :> {goal = {0.16, 0.12}}]

版权声明：本文为CSDN博主「robinvista」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：

https://blog.csdn.net/robinvista/article/details/118538616