广告
四轮转向汽车操纵稳定性建模与仿真
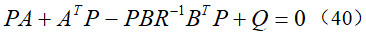
图10 前后轮转角输入
前轮转向车辆与四轮转向车辆的操纵动力学响应对比结果如图11-14所示。由图可见，四轮转向车辆的侧偏角远小于前轮转向车辆，且速度越快四轮转向车辆侧偏的控制效果越明显，同时，四轮转向车辆的横摆角速度随着车速的增加而减小，4WS车辆在侧偏抑制与横摆角速度控制方面的优势非常明显。由图14可见，4WS车辆的不足转向特性比两轮转向车辆更突出，在高速时将更好地抑制车辆侧偏与横摆运动，这也说明了4WS车辆的操纵稳定性比前轮转向车辆表现得更优异。
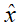
图11 侧向速度响应
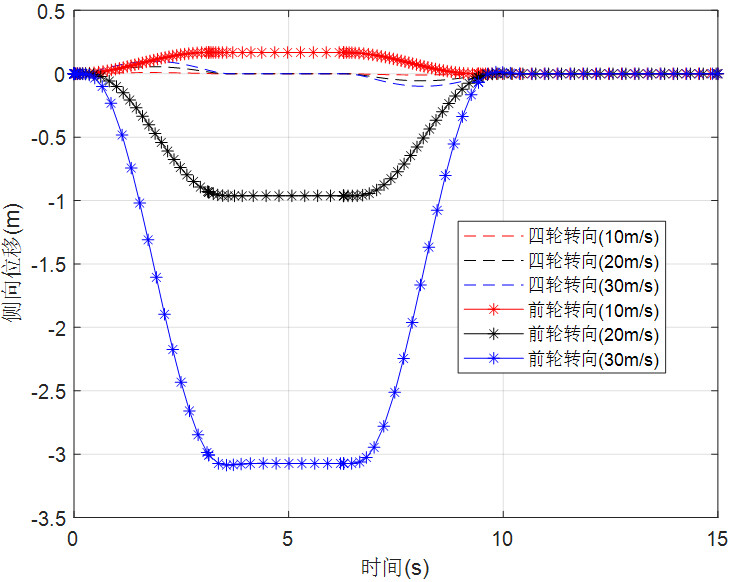
图12 侧向位移响应
图13 横摆角速度响应
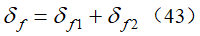
图14 车辆行驶轨迹
由上述两个仿真试验的对比结果可知，与前轮转向车辆相比，在相同的转向盘转角输入下，4WS车辆采用如(16)所示的控制策略给后轮施加一个转向角，改善了转向系统的响应特性，车辆侧向运动速度明显减小。采用4WS系统提高了车辆的瞬态响应及车辆转向时的横摆阻尼，同时也减小了横摆角速度的振动周期、响应峰值和车身侧偏角。由图可见，采用(21)来设定前后轮转向角之比Gδ时，4WS系统使得车辆转向过程中的侧偏角非常接近于0，从侧向动力学响应（如横摆角速度、侧向加速度等）来看，4WS车辆的控制效果也比前轮转向车辆的控制效果更好。
PID控制器
PID控制器是一种典型的动态输出反馈控制器，其控制律为
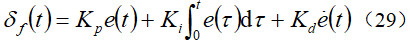
其中，Kp、Ki、Kd分别为误差的比例系数、积分系数、微分系数。PID控制器适用于单输入单输出系统，应用于前后轮转向车辆控制系统难度较大，因此，后轮转向角控制输入策略选择(16)，系统测量输出选择可测的横摆角速度，因此，可得单输入单输出系统模型为
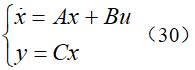
其中，
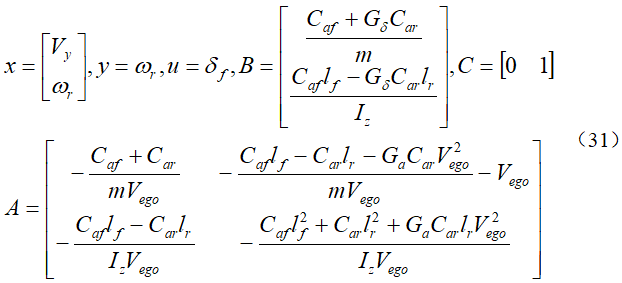
此时，系统(30)即为一个单输出单输出系统，可以针对该模型设计一个PID控制器。
假设期望行驶轨迹的转弯半径为R0，则期望的横摆角速度为：
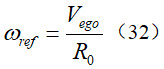
则PID控制器(29)的横摆角速度跟踪误差为
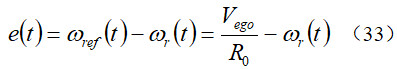
隆伯格状态观测器
利用全状态反馈控制可以非常方便地实现四轮转向控制，而不受限于后轮转向控制策略(16)。但是，4WS车辆模型(15)存在状态不可测问题，即横向速度不可测，而只有横摆角速度是可测的，同时，考虑横摆角速度的测量误差，因此，当设计状态反馈控制器时，需要先设计4WS车辆模型的状态观测器，以估计出系统的横向速度和横摆角速度并实现全状态反馈控制。因此，考虑单输入单输出的4WS车辆模型为
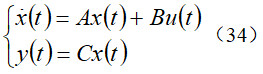
其中系统矩阵如(31)所示。接下来设计隆伯格观测器以重构4WS车辆的运动状态：
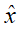
其中，
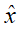
为x的状态估计值，Ke称为观测器的增益矩阵。隆伯格观测器利用可量测输出y与估计输出
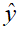
之差来对先验估计值进行修正，矩阵Ke起到加权修正的作用。
为了得到观测器的误差动态方程，定义跟踪误差为
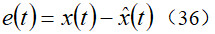
将(34)减去(35)可得
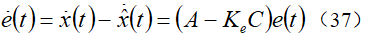
可见，误差向量的动态特性由矩阵A-KeC的特征值决定。如果矩阵A-KeC渐近稳定，则对任意初始误差e(0)，误差向量e(t)都将趋近于0，也就是说，
都将收敛到x(t)。因此，可以利用极点配置法对隆伯格观测器的增益矩阵进行设计。当给定系统矩阵A和C以及期望的观测器极点p后，可以利用下面的函数命令求得观测器增益矩阵Ke：
Ke=place(A',C',p)'
状态反馈控制器
当附加了后轮转角后，车辆横摆角速度和侧向运动速度的稳态增益随车速和前轮转角发生了较大幅度的变化，即同向转向时稳态增益减小，反向转向时稳态增益增大，这就增加了转向系统的控制难度。因此，可以用最优控制思想来设计4WS的控制策略。由于采用了(21)来设定前后轮转向角之比Gδ，4WS系统使得车辆转向过程中的侧偏角几乎为0，因此，4WS的最优控制问题可以描述为：在前后轮转向角之比Gδ和比例系数Ga已知的情况下，寻找一个最优的前轮转角输入使得4WS车辆的横摆角速度最小化，同时，考虑控制能量的最小化，因此，该最优控制的性能指标可定义为
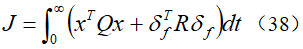
其中，
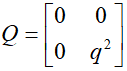
为权矩阵，q和R为权重系数。
广告 
广告
编辑推荐
最新资讯
-
测迅乌镇&盐城测试场：助力智能网联汽车标
2025-02-22 12:39
-
使用示波器对三相电机驱动器进行测量
2025-02-22 12:37
-
上汽集团大乘用车重磅招聘
2025-02-22 12:25
-
GB/T 44173-2024对开门预警DOW的要求
2025-02-22 12:25
-
声音工程：像用PS一样编辑声音
2025-02-21 17:04
广告
广告
