广告
四轮转向汽车操纵稳定性建模与仿真
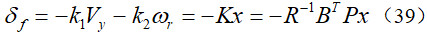
则性能指标J为最小，其中，P是黎卡提方程的解：
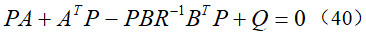
考虑到系统状态的不可测问题，利用观测器重构的状态进行反馈控制，即
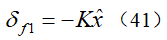
其中，
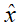
为利用隆伯格观测器(35)估计的x的状态值。
根据(24)所示的稳态横摆角速度响应，以及期望的横摆角速度(32)，可得4WS车辆稳态行驶时的前馈控制输入为：
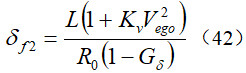
则采用前馈与反馈相结合的控制策略时的前轮转角输入为：
闭环系统仿真
假设观测器极点p=[-10,-20]，权重系数为q=5和R=1，利用以下代码求解观测器和控制器增益矩阵。vx=10;m=1920;Iz=3217;Cf=70000;Cr=110000;lf=1.55;lr=1.45;L=lf+lr;Ga=0.001;Gd=(Cf*lf*m*vx^2-Cf*Cr*lr*L-Ga*Cf*Cr*L*vx^2)/(Cr*lr*m*vx^2+Cf*Cr*lf*L);A=[-(Cf+Cr)/m/vx,-(Cf*lf-Cr*lr-Ga*Cr*vx^2)/m/vx-vx;-(Cf*lf-Cr*lr)/Iz/vx,-(Cf*lf^2+Cr*lr^2+Ga*Cr*lr*vx^2)/Iz/vx];B=[(Cf+Gd*Cr)/m;(Cf*lf-Gd*Cr*lr)/Iz];C=[0,1];p=[-10,-20];Ke=place(A',C',p)';
Q=[0,0;0,10];R=1;K=lqr(A,B,Q,R);
求解结果如下：
Ke=[-2.5820;7.7123],K=[0.0281,1.9669]
假设车辆行驶速度在10m/s附近波动，期望的圆周轨迹半径为50m，即期望轨迹的曲率为0.02。设计四轮转向车辆的圆周轨迹跟踪控制器，并完成4WS车辆的闭环仿真。对比四轮转向和两轮转向车辆的轨迹跟踪性能，以及PID控制和基于隆伯格观测器的LQR状态反馈控制效果，系统仿真结果如下图所示。
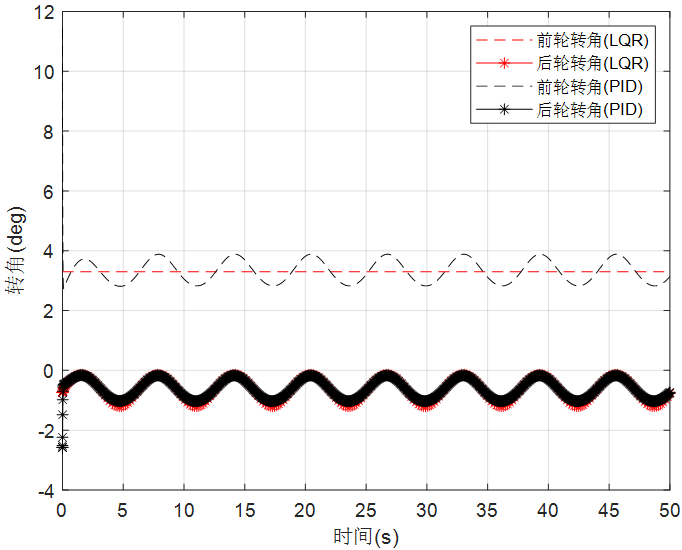
图15 前后轮转角输入
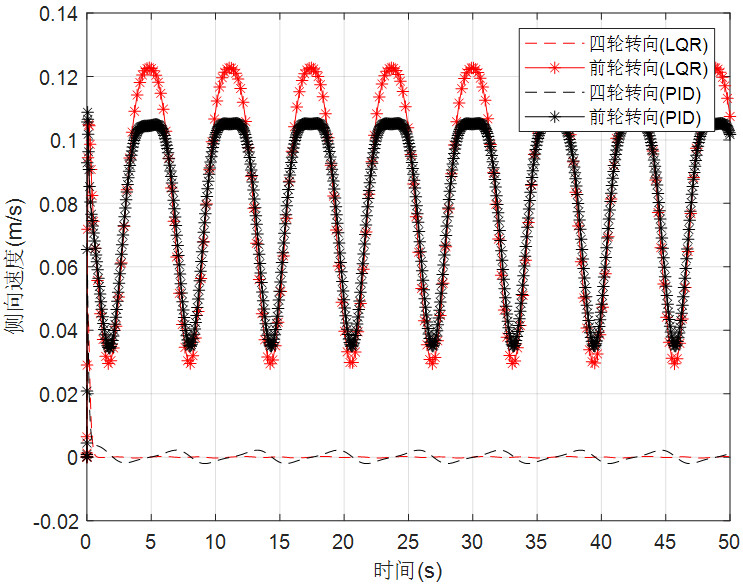
图16 侧向速度响应
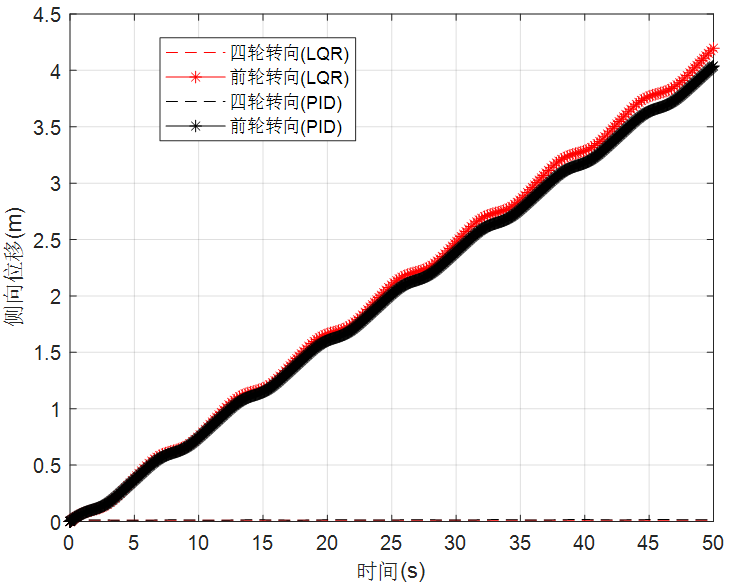
图17 侧向位移响应
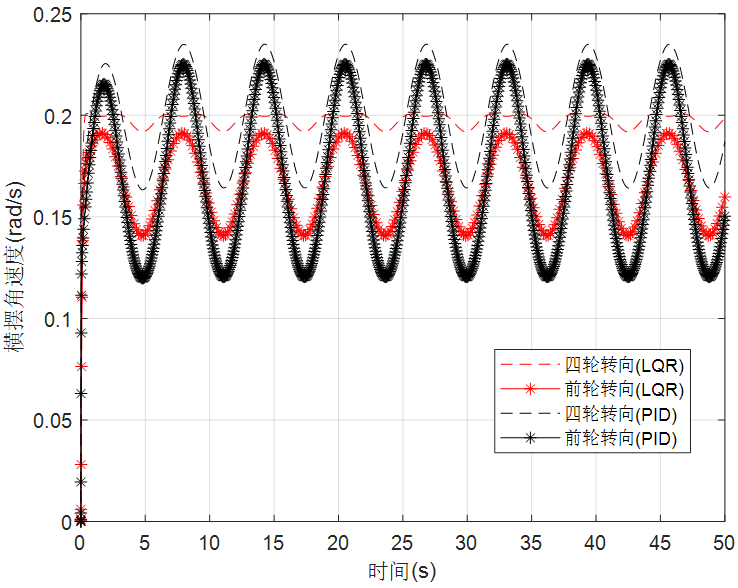
图18 横摆角速度响应
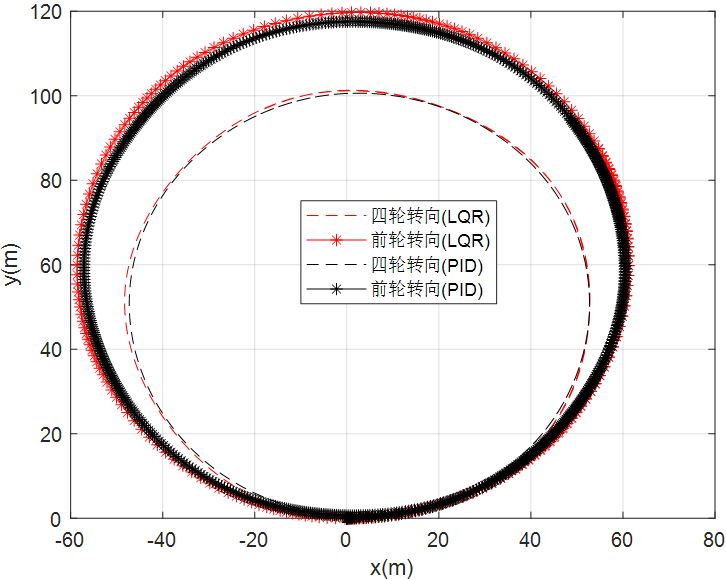
图19 车辆行驶轨迹
由仿真结果可见，四轮转向车辆的轨迹跟踪性能优于前轮转向车辆，由于车速为10m/s，小于临界车速，因此四轮转向车辆是逆位转向模式，故四轮转向车辆的横摆角速度略高于两轮转向车辆。LQR的控制效果也优于PID的控制效果，在PID的仿真结果中出现了大幅度的振荡，由PID控制的四轮转向车辆也出现了微小的侧偏，而在LQR控制的四轮转向车辆中几乎没有侧偏发生。综上，采用前馈与反馈相结合的方式，并利用隆伯格观测器重构系统状态后用于反馈控制，观测器和控制器分别采用极点配置法和LQR求解，采用这种控制策略的四轮转向车辆能获得较优的轨迹跟踪性能。
广告 
广告
编辑推荐
最新资讯
-
测迅乌镇&盐城测试场：助力智能网联汽车标
2025-02-22 12:39
-
使用示波器对三相电机驱动器进行测量
2025-02-22 12:37
-
上汽集团大乘用车重磅招聘
2025-02-22 12:25
-
GB/T 44173-2024对开门预警DOW的要求
2025-02-22 12:25
-
声音工程：像用PS一样编辑声音
2025-02-21 17:04
广告
广告
