集成轮侧减速电驱动系统双拖臂悬挂机构参数优化研究

编者按：随着电动汽车技术的不断发展和进步，对于车辆驱动总成的布置形式有着较多的方案可供选择，但分布式驱动依靠其自身在结构设计、控制方法、集成性能等方面的诸多优点逐渐成为电机驱动布置模式的首选。分布式电机驱动布置方案大致可以分为两种类型：轮毂电机驱动和轮边电机驱动。选用轮毂电机可以节省大量的中间传动件，优化车辆结构，同时可以实现驱动方式，并且能够耦合多种新能源汽车的传动要求，但同时也存在簧下质量较大和电机制动性能有限等缺点。轮边电机布置方案可以很好的实现电子转速和转矩协调控制，并且可以回收制动能量，但其电机控制的可靠性也是不容忽视的问题。本文提出了一种基于轮侧电机双拖臂悬挂机构参数研究方法，很好地解决悬架结构参数与驱动方案的适用性问题。

本文译自：

《Research of parameter optimization of double trailing arm suspension mechanism for integrated wheel side deceleration electric drive system》

文章来源：

Journal of Physics: Conference Series, 2021, 1939(1):012011-

作者：

Chen Xinbo, Lu Yanjia, Xu Naiwen, Xu Xiang

原文链接：

https://iopscience.iop.org/article/10.1088/1742-6596/1939/1/012011/meta

摘要：通过将拖臂悬架与车轮侧减速电驱动系统相结合，本文提出了双拖臂悬架车轮侧减速电动驱动系统的解决方案。建立了基于四杆机构的双拖臂悬架的几何数学模型。编制了MATLAB可执行文件和程序接口，在给定条件下快速定位电机中心布局位置。当车轮跳动时，电机和车轮之间的中心距离保持不变。根据MATLAB提供的合理拖臂结构参数，进行CATIA三维建模，并引入ADAMS进行运动学仿真，验证了双拖臂悬架设计方案和MATLAB程序的可行性。

1 介绍

人们越来越重视环境保护。节能减排势在必行。寻找新型节能环保“零排放”汽车已成为一种趋势。尤其是电动汽车，因为其低排放和低能耗而备受关注。
根据电机驱动模式，电动汽车通常分为两种类型：集中驱动和分布式车轮驱动。集中驱动采用传统的汽车结构布局，但其结构复杂，传动效率低，左右驱动轮无法独立控制。车轮侧驱动系统直接将驱动电机布置在车轮中或附近。与集中驱动系统相比，它具有集成度高、效率高、可控性强、结构简单等优点。然而，电动车轮的簧下质量显著增加，簧上质量与簧下质量之比失衡，导致车辆性能恶化[1]。参考文献[2]中提出了具有单摆臂悬架的车轮侧电驱动系统，并通过理论推导证明，在悬架摆臂上合理布置车轮侧减速电驱动组件的质心位置，可以大大降低车轮侧减速电驱动系统的等效簧下质量。本文介绍了一种双拖臂悬架轮侧电驱动系统的结构。在这种结构下，电机布置在框架中，如图1所示。因此，电机的簧下质量被传递到簧上质量，以进一步减少簧下质量，这可以有效提高车辆的驾驶性能[3]。由于齿轮传动精度要求高，中心距离有限，噪音大，必须考虑其润滑、密封和其他限制。因此，在电机与车轮之间设置传动机构时，考虑采用链条传动或同步带传动，具有中心距可调、抗冲击能力强、运行稳定、重量轻、成本低等优点。然而，由于电机布置在框架上，从电机输出轴中心到车轮中心的距离将随着车轮跳动而随悬架结构参数而变化。因此，有必要对车轮侧悬架结构进行设计和分析，以便找到合适的悬架结构布局。同时，选择可变中心距或中心距在小范围内变化的变速器模式，可以有效降低道路激励对轮侧驱动变速器系统的影响。

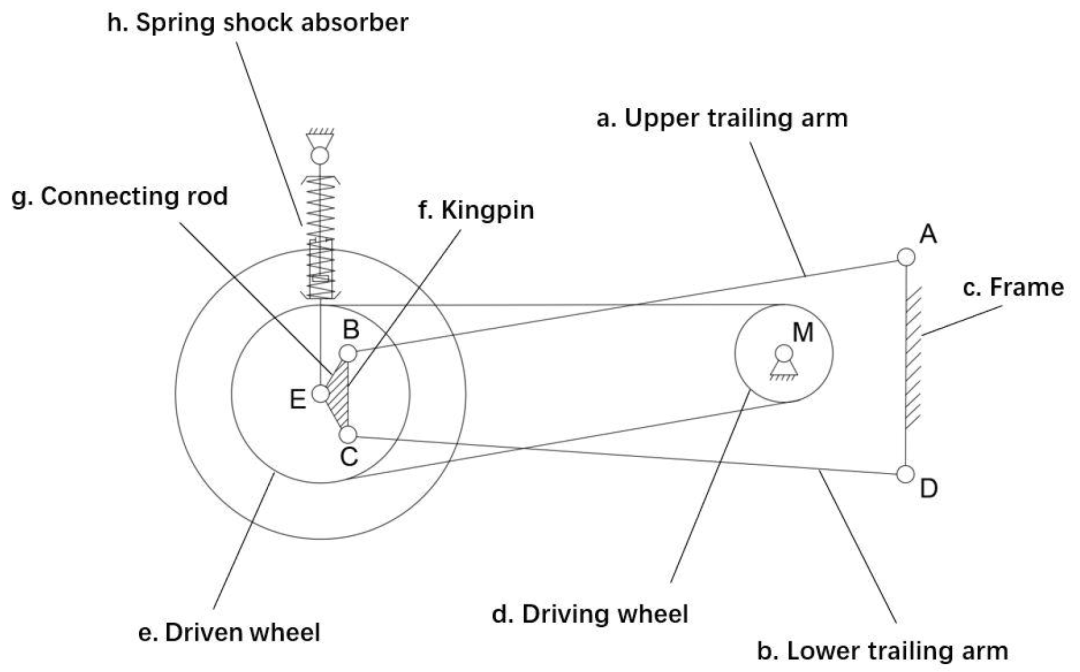
图 1双拖臂悬架轮侧电驱动系统结构图，电机安装在车架上
2 理论设计

双后臂悬架轮侧减速电驱动系统理论结构设计方案如图2所示。电机固定在车架上，且电机与驱动轮在同一轴上，为车架；、为上、下拖臂；为主销，、为上下后臂和车架的铰点；、为上下后臂和主销的铰点；是车轮中心。车轴固定在主轴上。在图2中，框架、上下后伸臂和主销构成一个铰链式四杆机构。连杆与主销6合并为一个整体，点在连杆上；点在机架上，这是电机输出轴的中心。当车轮跳动上下，为车轮中心点E要实现的圆弧轨迹。即圆心，半径的圆弧轨迹。因此，将问题转化为按照预定轨迹求解四杆机构设计参数。如果能找到双后伸臂长度、主销长度、等效车架长度等合理参数，使车轮在路面激励下沿理想圆弧轨道跳跃，并将电机中心布置在点(主动轮中心)，则从动轮与主动轮的中心距离不变，则系统方案是可行的。

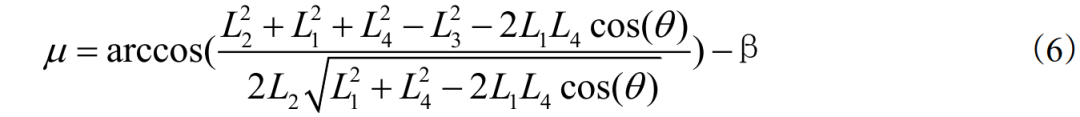
图2  双后臂悬架理论结构设计方案系统框图建立平面直角坐标系，点为原点，坐标系与轴重合。设杆、、、、的长度分别为、、、、。为水平线与杆的夹角，为水平线的夹角，为杆与杆的夹角，。在中，使用余弦定理:

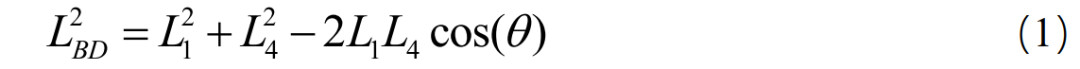
以及

由式（2）可得

在中，根据余弦定理，可计算为:

因此

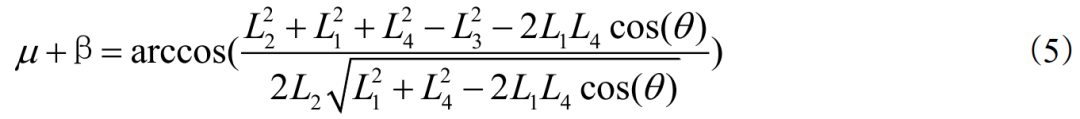
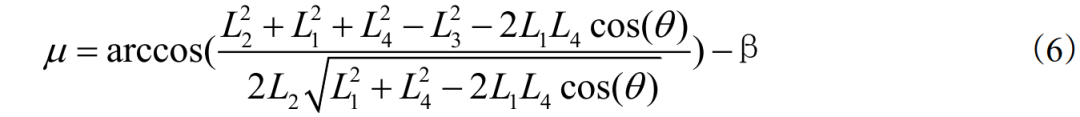
根据上式，点的坐标可表示为:

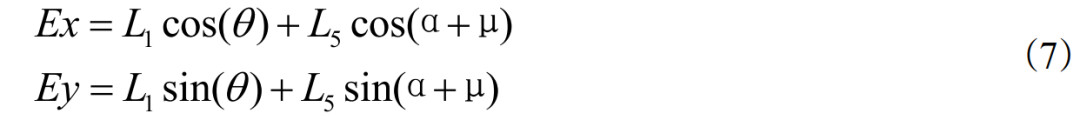
3 参数优化

双后伸臂悬架机构优化设计的可变参数为：上后伸臂长度，主销长度，下后伸臂长度，等效车架长度，连杆长度，电机中心点坐标，车轮跳动拟合圆半径。优化的一般数学表达式如式（8）所示，其中优化目标是使车轮跳动时车轮运动中心轨道上各点到电机中心点距离的均方根与拟合圆半径R之间的差值最小。约束条件是四杆机构长度条件，即任意三杆的长度之和大于第四杆。

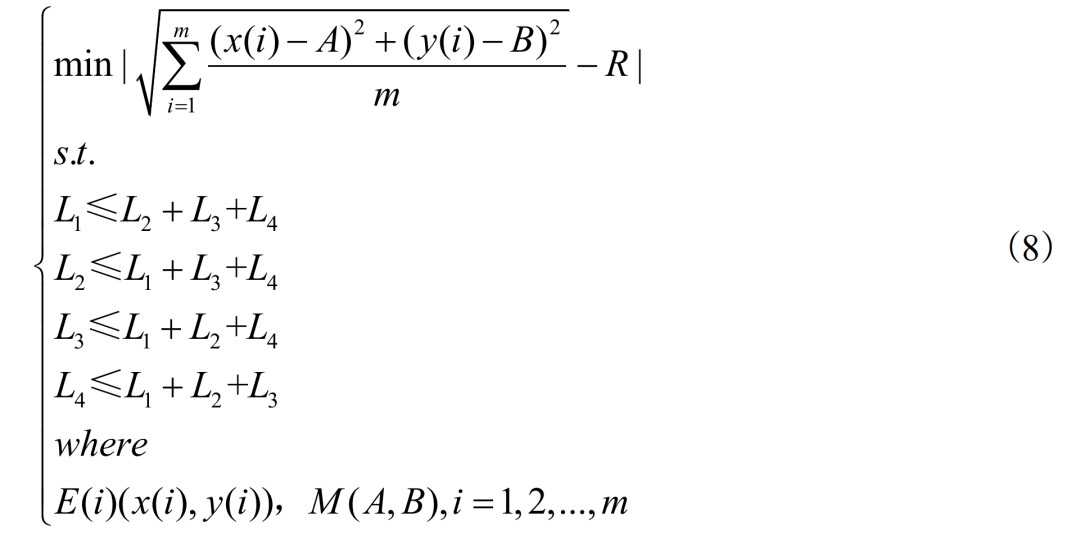
在上述理论分析的基础上，对双后臂悬架轮侧减速电驱动系统进行了分析，为了在给定条件下快速定位电机中心布局，编译了MATLAB可执行文件。优化流程图如图3所示，初始可执行程序界面如图4所示。

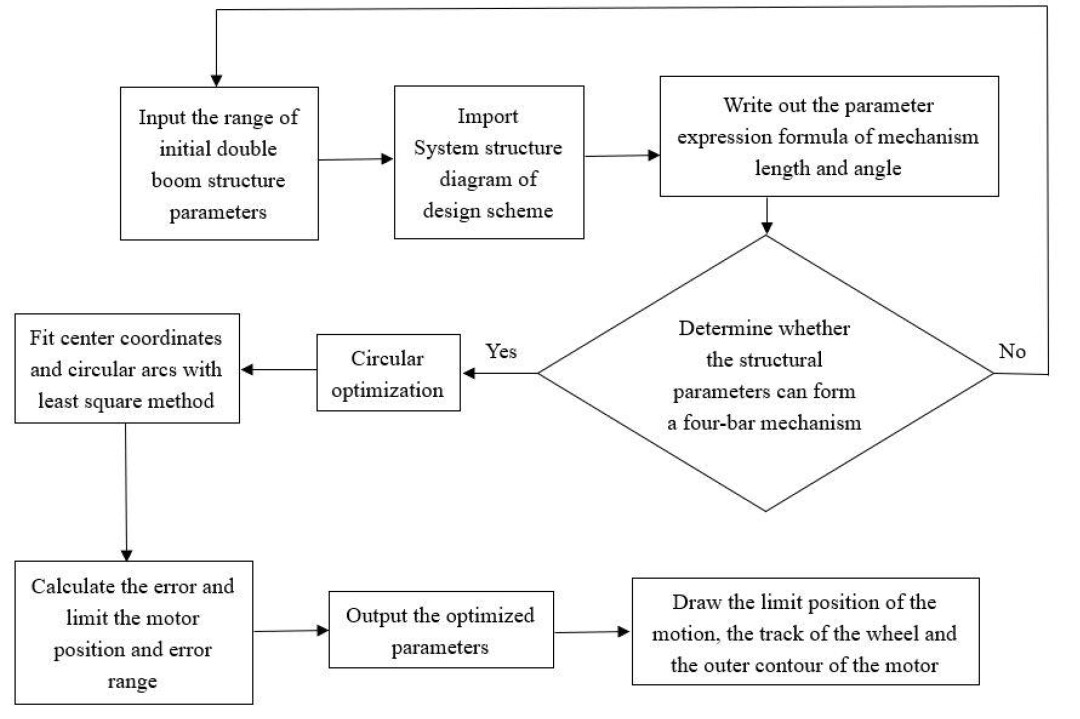
图3  优化流程图

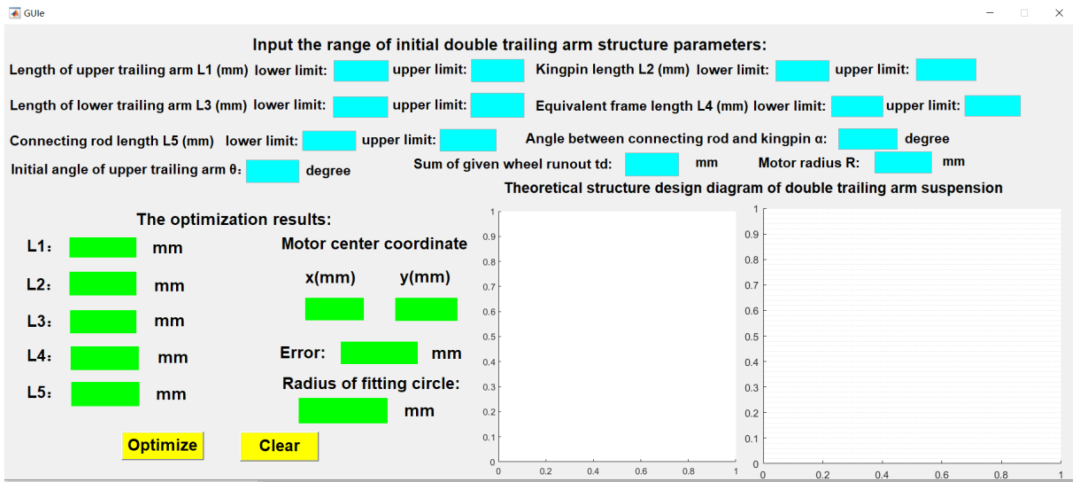
图4  MATLAB可执行程序初始界面

该程序使用五个循环优化。循环变量为上拖臂长度、主销长度、下拖臂长度、等效齿条长度和连杆长度。循环步长为1mm。首先，根据前一节中的理论分析公式，编制了相应的MATLAB程序。此外，还列出了机构长度和角度参数的相应表达式。然后验证相应的机构参数是否满足四杆机构存在条件，即任意三杆的长度和大于第四杆。如果不满足条件，将输出警告，如果满足条件，则将继续执行。然后用最小二乘法拟合圆心坐标和圆弧，并将误差限制在给定范围内。然后得到了四杆机构的优化参数以及电机布局的位置、尺寸和相应的误差。最后，绘制了电驱动系统的极限位置、车轮中心轨迹和电机转速曲线。

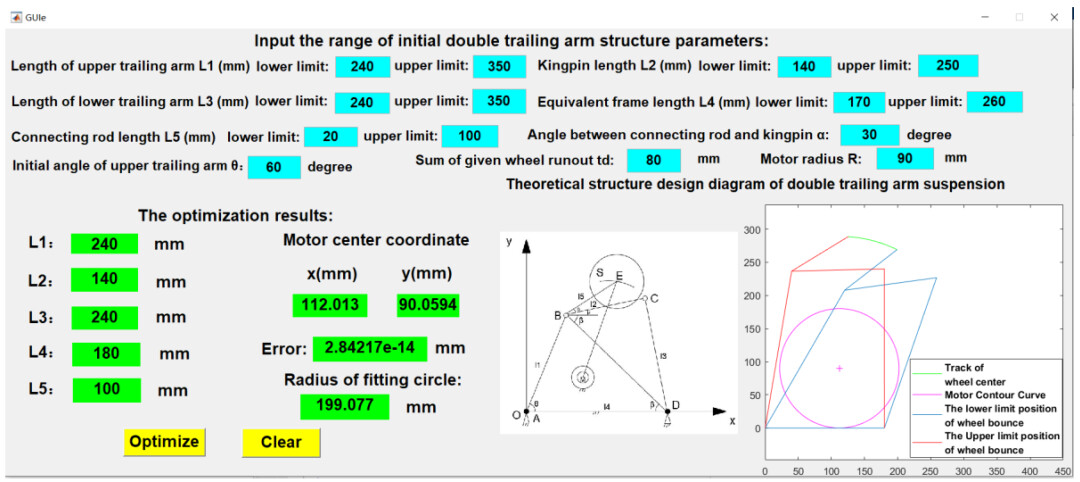
通过编程获得的程序窗口如图5所示。左侧的图像是双拖臂悬架电动驱动系统的结构图；左下区域用于显示节目图像；红线和蓝线是车轮跳动时的上限和下限位置，绿线是车轮中心的相应轨迹，粉色圆圈表示电机的外部轮廓，中心表示电机中心。执行程序后，单击黄色的“清除”按钮以清除界面。首先，需要在上部蓝色文本框中输入初始双拖臂结构参数的大小范围。这里，上拖臂长度的变化范围为[240350]mm。主销长度为[140250]mm，下拖臂长度为[240350]mm；等效车架长度为[170260]mm，连杆长度为[20100]mm。连杆和主销之间的角度为30°，上拖臂的初始旋转角度为60°，给定的车轮跳动总和为80mm，电机半径为90mm。单击黄色的“优化”按钮，优化结果如图4所示。优化结果将在程序窗口左下方的绿色文本框中输出。优化结果为：上拖臂长度=240mm，主销长度=140mm，下拖臂长度=240mm，等效框架长度=180mm，连杆长度=100mm。电机中心坐标为（112.013,90.0594）mm，拟合误差为，拟合圆半径199.077mm。

编写了MATLAB可视化界面（GUI）。它非常方便，界面清晰直观。只需输入初始参数范围，然后单击“优化”按钮即可快速找到电机中心位置和相关组件的适当参数。

图5 MATLAB可执行程序优化结果界面

4 实体莫信号建立和验证

4.1. CATIA参数建模

基于上一节中获得的优化参数，通过CATIA软件构建三维模型，如图6所示。上拖臂长度=240mm，主销长度=140mm，下拖臂长度=240mm，等效框架长度=180mm，连杆长度=100mm，主销与连杆之间的角度为30°，上拖臂的初始旋转角度为60°，电机半径为90mm。根据上一节中获得的优化中心布置电机中心，省略了大、小同步滑轮的模型，将大、小滑轮的等效质量传递到等效的上、下拖臂和主销上，以实现简化。

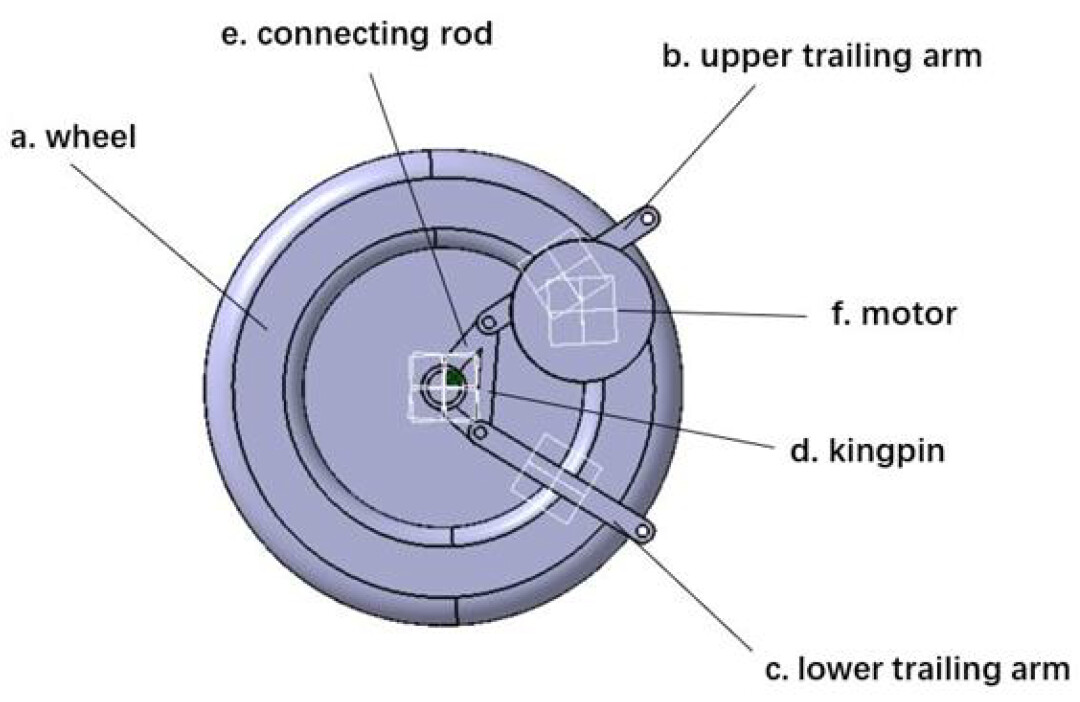
图6 双拖臂悬架车轮侧电驱动系统CATIA 3D模型

4.2.ADAMS参数验证

将CATIA 3D模型导入ADAMS，然后需要定义相关零件的属性和约束，因为零件之间的关系是无约束的。

图7 双拖臂悬架虚拟模型

将双拖臂悬架轮边减速电驱动系统模型导入ADAMS后，根据双拖臂悬挂轮边结构的运动关系，考虑如图7所示的约束关系。其中，在电机与上拖臂之间增加固定副约束，在车轮与主销之间增加固定副约束，在上拖臂、主销和车体之间增加转动副约束。转动副的旋转点为上拖臂的两个铰接端，旋转轴方向垂直于纸面。再在下拖臂、主销和车体之间相应增加一个旋转副约束。在车体和轮之间增加一个沿上下方向的移动副，在试验台和地面之间也增加一个移动副。车身与主销、车轮与试验台采用弹簧连接，弹簧刚度和阻尼按表1参数配置，各部分质量按表1定义建立约束关系。

表1 双拖臂悬架系统仿真模型参数

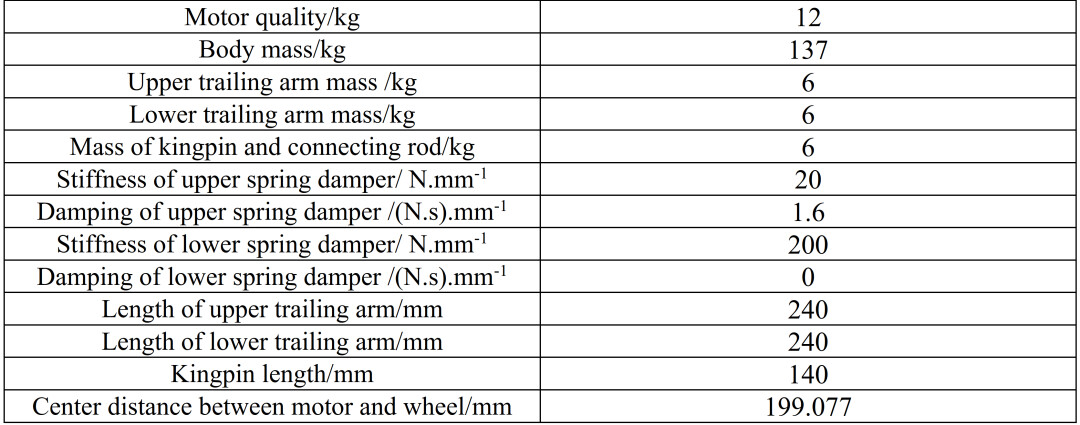
由于上一节中给定的车轮跳动总和为80mm，因此通过在车轮与试验台之间的移动副上增加驱动来模拟道路输入激励。设置仿真时间为10s，仿真步长为500，并运行仿真。利用ADAMS中的测量及后处理模块，得到电机与车轮中心距随车轮上下跳动变化的曲线，曲线如图8所示。

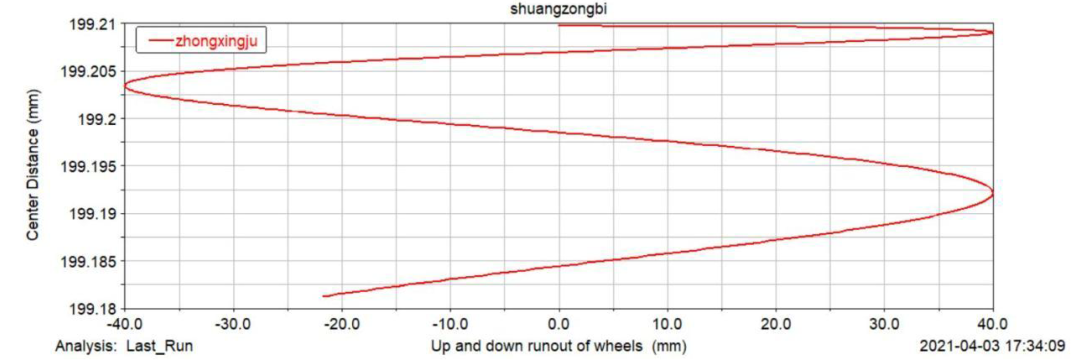
图 8 双拖臂悬架模型电机与车轮中心距随车轮上下跳动变化曲线

我们可以观察到电机与车轮中心距的平均值为199.2003mm，最小值为199.1813mm，最大值为199.2098mm。中心距最大偏差为0.0285mm，误差较小，在可接受的偏差范围内（＜0.1mm）。因此，在可接受的误差范围内，可以合理设计拖臂的尺寸参数和电机中心的位置，保证车轮与电机中心的中心距在可接受的范围内变化。本节中的仿真也验证了上一节中的MATLAB程序。

5 结论

(1)本文提出了一种双拖臂悬架轮侧电驱动方案，建立了基于四杆机构的双拖臂悬架几何数学模型。通过将电机质量转移到车架上，有效降低了簧下质量，提高了传动效率和空间利用率。

(2)采用MATLAB理论编程方法对双拖臂悬架电驱动系统四杆结构参数进行优化，解决了当车轮弹跳且电机安装在车架上时，车轮中心与电机输出轴心的距离会随悬架结构参数变化的问题。选用优化后的四杆结构参数来使中心距不变或在可接受范围内是具有实用性的。开发了GUI程序，使程序窗口化且界面清晰直观。

(3)根据优化后的四杆结构参数，在ADAMS中建立模型并进行仿真，且中心距的变化范围在传动机构可接受的范围内。通过综合验证，验证了这组参数的可行性。同时，也验证了理论推导和编程实现的可行性和准确性。

参考文献