广告
一种考虑内部温度梯度的电池阻抗模型
摘要
电池模型常被应用于描述电池的动态特性并且可以被用来估计电池状态。由于充放电过程的影响，电池产热会造成电池内部温度和表面温度的不均一性。本文提出一种电池阻抗模型以提升电池模型性能，该模型考虑了电池内部温度梯度对于电池阻抗的影响。文章通过实验验证了该模型的有效性。结果表明使用该模型得到的EIS（电化学阻抗谱）与实验值具有良好的一致性，绝对最大误差仅为0.31。
不考虑温度梯度的电池建模与参数确定
图 1为电池的等效电路模型和EIS示意图（仅考虑虚部的负半边）。如图 1所示，每个EIS图均有高频率区，中频率区，与低频率区。高频率区的阻抗谱是一个接近实半轴的点，这意味着其可以代表欧姆内阻。中频率区的阻抗谱是一个平滑的半圆，可以将其看作是一个电阻与一个常相位角元件（constant phase angle element，CPE）共同作用的结果。最后低频率区是一条斜直线，可以理解为CPE单独直接作用的原因。CPE满足如下公式：
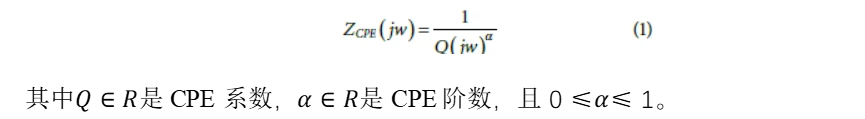
而图 1显示了总体等效电路模型，其频域的阻抗模型方程式如下：
而根据欧拉公式，公式（2）又可转化为如下公式：
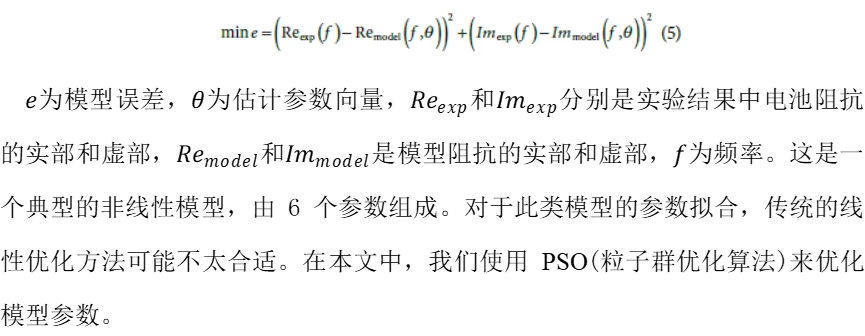
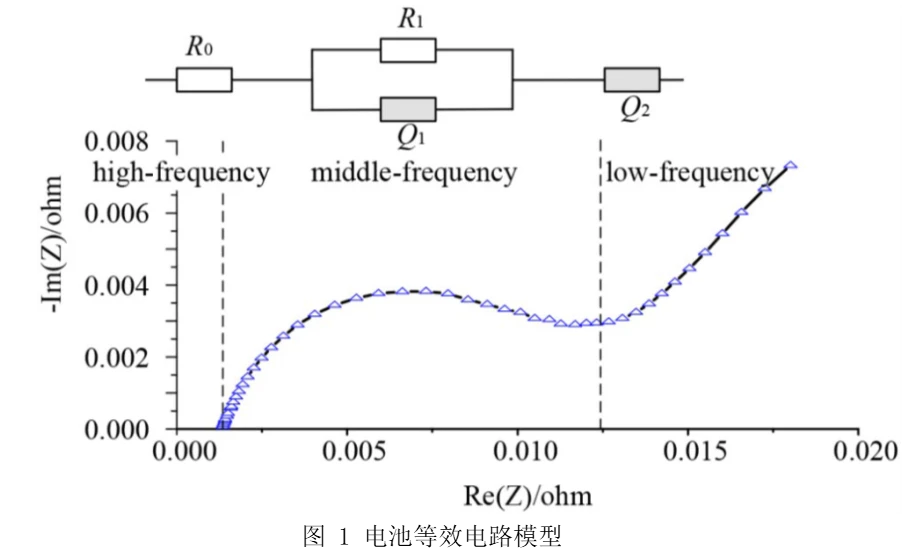
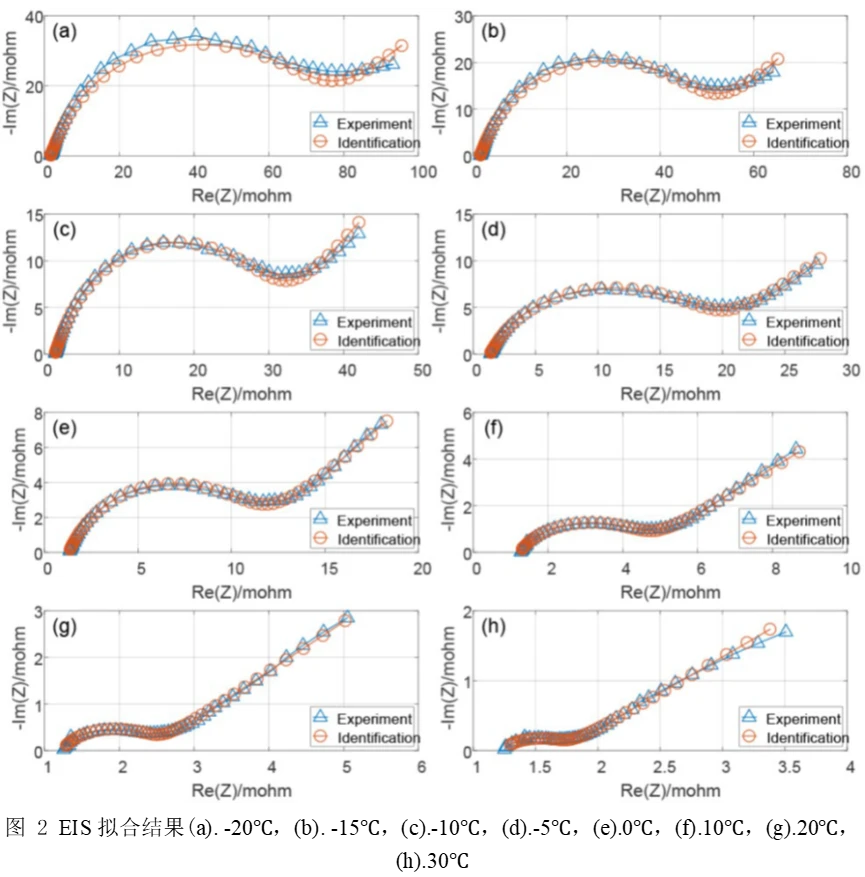
图2展示了SOC= 0.5下模型和实验数据之间的EIS比较结果。从拟合结果可以看出，在-10，-5，0，10和20，实验EIS和拟合EIS几乎重合。在3的低频区域拟合EIS具有最小的误差，在-20和-15的中频区域存在小误差。拟合结果表明，PSO算法是有用的，仿真参数可以用于离散建模。
考虑温度梯度的电池建模与参数确定
图 3为离散建模的示意图。Th其中是加热板温度，Tc是腔温度，并且有N个等效的单元在电池内部并联。假定温度分布是线性的，这样根据电池表面温度可以轻松推导出每个单元的温度。最高温度是加热板温度，最低温度是腔温度。在正常工作条件下，没有加热板，最高温度是内部温度，最低温度是表面温度，利用线性化假设，可以按照以下方式计算每一单元的温度：
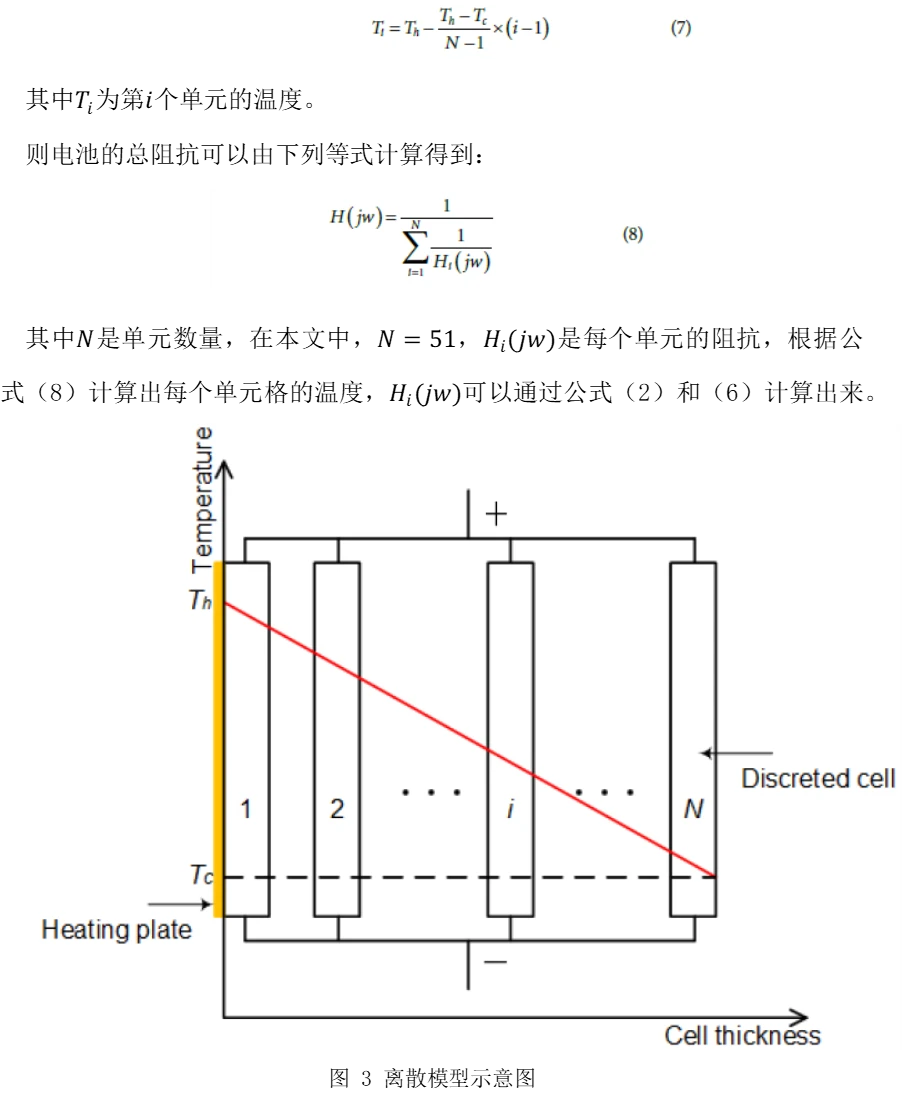
图 4为根据公式（8）计算的EIS，与实验结果测得的EIS的比较图。从图中可以看出，在不同的实验中，不同的温度梯度下，文章所提出的离散模型的EIS与实验EIS在高频和中频区域相符。但在低频区域，拟合EIS的斜率比实验EIS小，且误差不规律。这可能是由于β的值不变引起的，应进行更多的实验来发现β与温度之间的关系。
图 5显示了所提出的离散模型的误差。最大绝对误差为0.31毫欧，最大相对误差小于8.5%，上述误差可以接受，这表明所提出的离散模型表现良好。当电池内部存在温度梯度时，文章提出的离散模型可以更准确地描述实际电池的动态特性。
结论
-
1. EIS与SOC的状态没有太大的关系但温度对EIS特性影响重大。并且温度梯度也会影响电池阻抗。
-
2. 文章提出了一种离散模型（用于估算电池EIS特性），该模型的绝对最大误差（同实验结果相比）为0.31毫欧，相对最大误差小于8.5%。上述体现了该模型的良好效果。
-
3. 这篇文章研究了温度梯度对于电池EIS的影响，在离散化建模的帮助下，我们可以更准确地确定实际电池的动态特性。在接下来的研究中，EIS与老化状态之间的关系将可以进行研究，所以文章提出的离散建模方法可以被进一步应用在更多研究领域。
广告
广告
编辑推荐
最新资讯
-
【进博频道】闪耀进博，HIOKI新质生产力与
2024-11-06 07:48
-
TÜV NORD与上汽大通签订WVTA整车认证框架
2024-11-06 07:41
-
通过学习轮胎模型利用3分钟数据实现自主漂
2024-11-06 07:40
-
标准立项 ||《乘用车智能底盘矢量及舒适加
2024-11-06 07:39
-
标准立项 ||《乘用车智能底盘矢量及舒适加
2024-11-06 07:38
广告
广告
